Розы гвидо гранди

1.

РОЗЫ ГВИДО гранди.
Научный руководитель:
Никитина Лидия Павловна

2.

ЦЕЛЬ: Показать принцип построения линий в
полярной системе координат с помощью
формул перехода от декартовых координат к
полярным координатам.

3. Розы Гвидо Гранди

Задачи:
Проанализировать литературу по заявленной
теме
• Провести обзор различных систем координат.
• Изучить переход от декартовой системы
координат к полярной и обратно;
• Научиться строить график в полярной
системе с помощью Excel.
• Исследовать изменения вида кривой, в
зависимости от параметров входящих в её
уравнение;
• Познакомиться с некоторыми
замечательными кривыми известных
математиков.

4. Розы Гвидо Гранди

Итальянский геометр
Гвидо Гранди (1671–1742),
работая с полярной системой
координат, решил воссоздать с
помощью линий эти прекрасные
растения. Полученный результат
он назвал розами (итал. rosa).

5. Розы Гвидо Гранди

Розы Гвидо Гранди радуют глаз правильными и плавными линиями, но их очертания не каприз
природы— они предопределены специально подобранными математическими зависимостями

6.

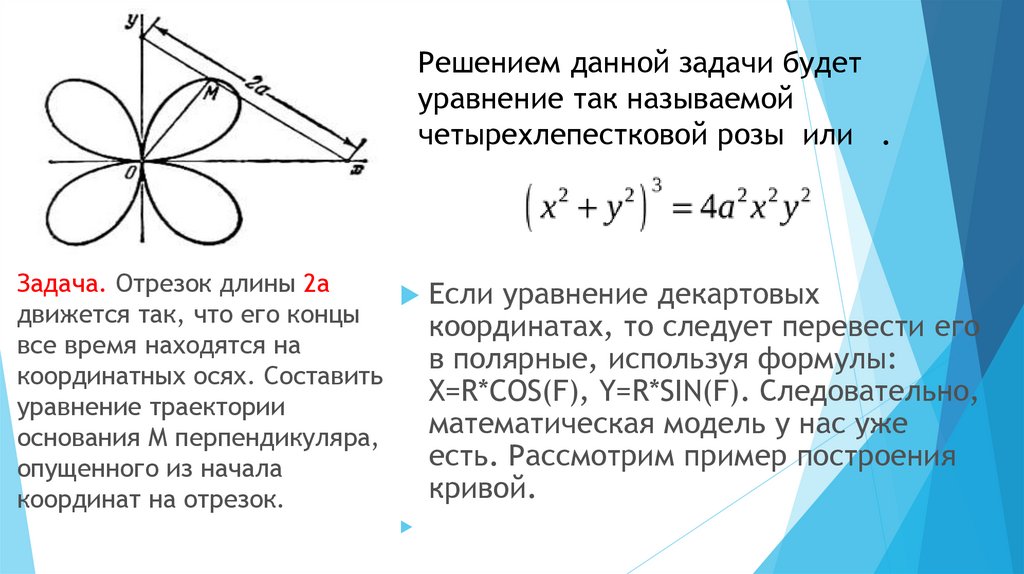
Решением данной задачи будет
уравнение так называемой
четырехлепестковой розы или .
Задача. Отрезок длины 2а
Если уравнение декартовых
движется так, что его концы
координатах, то следует перевести его
все время находятся на
в полярные, используя формулы:
координатных осях. Составить
X=R*COS(F), Y=R*SIN(F). Следовательно,
уравнение траектории
математическая модель у нас уже
основания М перпендикуляра,
есть. Рассмотрим пример построения
опущенного из начала
кривой.
координат на отрезок.

7. Розы Гвидо Гранди

Фигуры
в полярных координатах
образуются как след конца бегающего по
кругу полярного радиуса переменной
длины. Длина полярного радиуса
определяется величиной угла, который в
данный момент времени он образует с
полярной осью

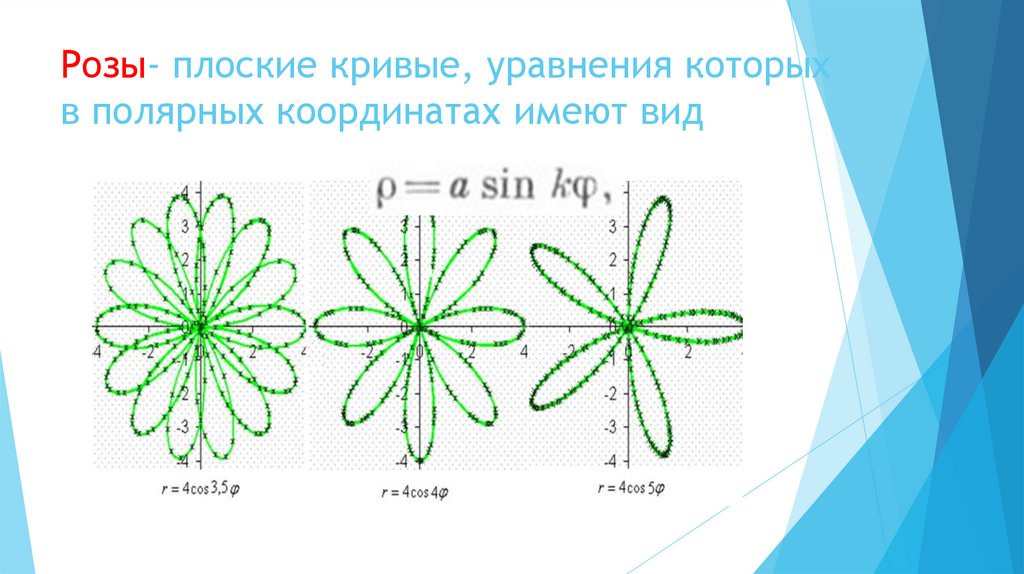
8. Розы- плоские кривые, уравнения которых в полярных координатах имеют вид

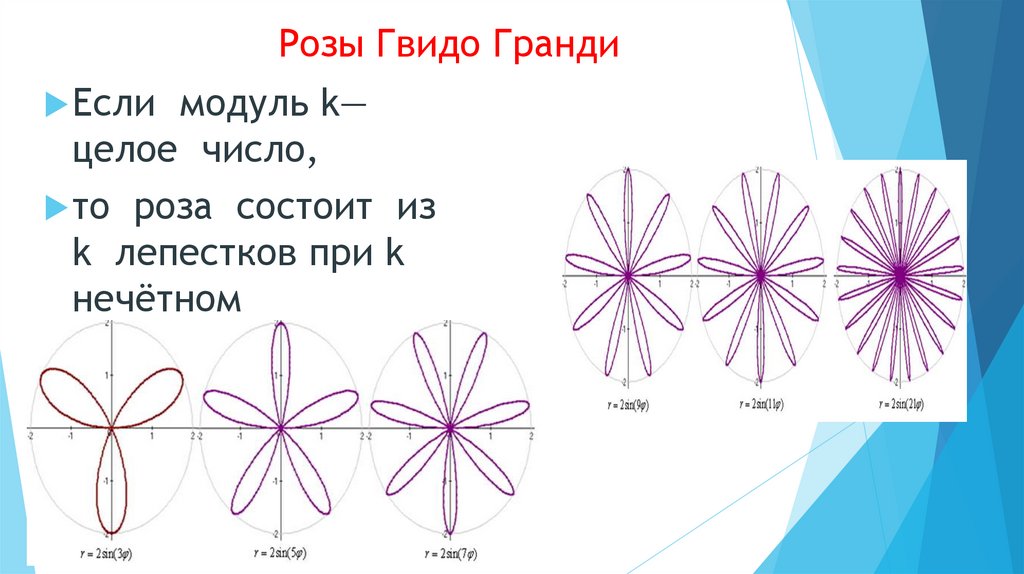
9. Розы Гвидо Гранди

Если
модуль k—
целое число,
то роза состоит из
k лепестков при k
нечётном

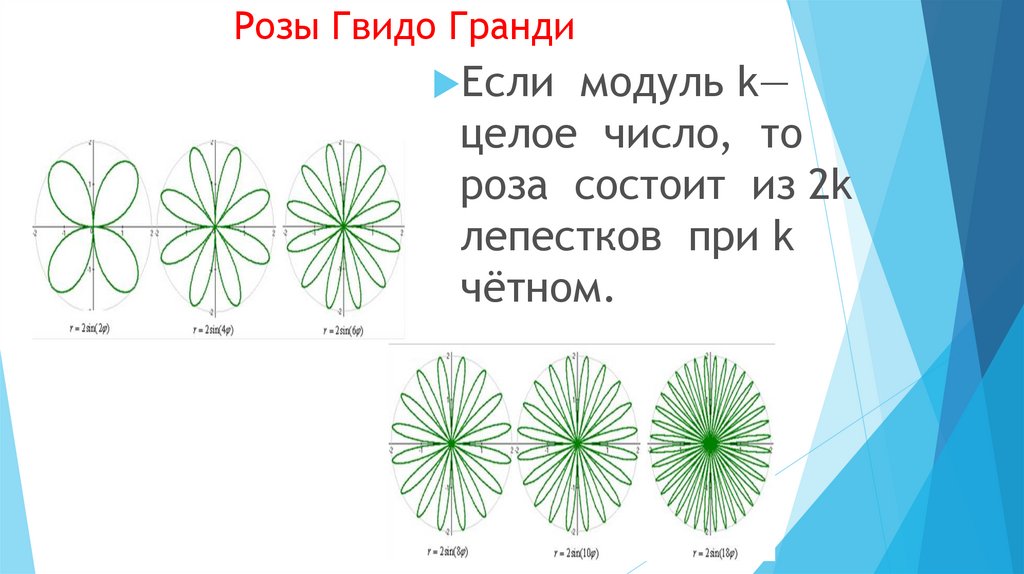
10. Розы Гвидо Гранди

Если
модуль k—
целое число, то
роза состоит из 2k
лепестков при k
чётном.

11. Розы Гвидо Гранди

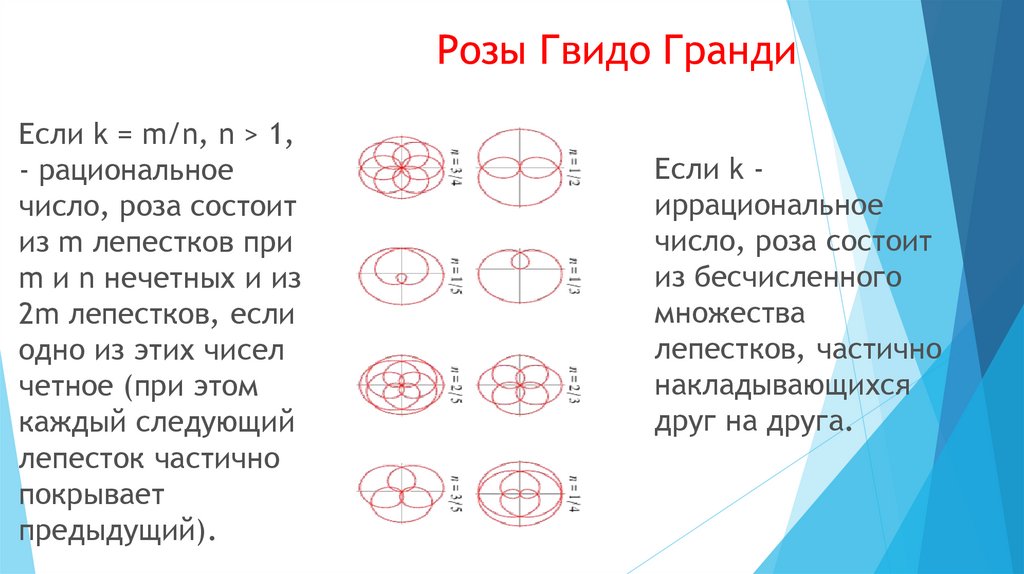
Если k = m/n, n > 1,
- рациональное
число, роза состоит
из m лепестков при
m и n нечетных и из
2m лепестков, если
одно из этих чисел
четное (при этом
каждый следующий
лепесток частично
покрывает
предыдущий).
Если k иррациональное
число, роза состоит
из бесчисленного
множества
лепестков, частично
накладывающихся
друг на друга.

12. Розы Гвидо Гранди

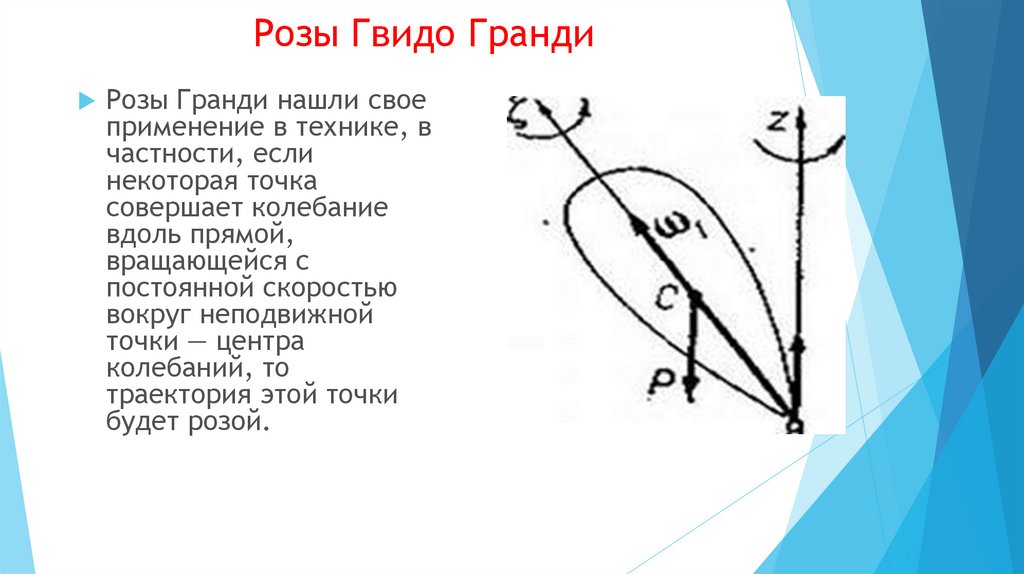
Розы Гранди нашли свое
применение в технике, в
частности, если
некоторая точка
совершает колебание
вдоль прямой,
вращающейся с
постоянной скоростью
вокруг неподвижной
точки — центра
колебаний, то
траектория этой точки
будет розой.

13. Список используемой литературы и сайты и ссылки

1.
Д.В. Беклемишев. Курс аналитической геометрии
и линейной алгебры. Москва, Наука, 1980 г.
2.
И.М. Гельфанд и др. Метод координат. Москва,
Наука, 1973 г.
3.
В.С. Шипачёв. Основы высшей математики.
Москва, Высшая школа, 1989 г.
4.
И.А. Каплан. Практические занятия по высшей
математике, Харьков, Харьковский университет, 1970 г.
5.
И.И. Привалов. Аналитическая геометрия,
Москва, Высшая школа, 1966 г.
6.
Н.В. Ефимов. Краткий курс аналитической
геометрии. Москва, Высшая школа, 1972
7.
Г.И. Запорожец. Руководство к решению задач по
математическому анализу. Москва, Высшая школа, 1974
г.
http://www.ipfw.edu/math/Coffman/pov/spiri
c.html - рассказано о сечениях тора с
картинками на английском языке. Там же
ссылки на биографии математиков и на
замечательные кривые.
2. http://www.didaktik.mathematik.uniwuerzburg.de/mathei/cinderella/cassoval.html
- ссылка на апплет, рисующий овалы
Кассини, на немецком языке.
3.
http://164.8.13.169/Enciklopedija/math/math
/c/c084.htm страничка овалов Кассини сайта,
посвященному замечательным кривым.
4. http://www-gap.dcs.stand.ac.uk/~history/Mathematicians/Cassini.htm
l подробная биография Кассини
5. http://rusgraf.ru/graf4
6.
http://www.2dcurves.com/higher/highercc.htm
l прекрасная страничка для любителей
красивых кривых, из нее мы узнали об овалах
с тремя и более фокусами.
8.
Б.П. Демидович. Сборник задач и упражнений по
математическому анализу, Москва, Наука, 1969 г.
9.
Егерев В.К. Радунский Б.А., Тальский Д.А.
Методика построения графиков функций. Москва, 1970 г.
10.
Дороднов А.М. Краткие сведения о построении
графиков в полярной системе координат. Москва, 1972 г.
11.
Линии: определение, исследование и построение:
Метод. рекомендации / Краснояр. гос. ун-т; Сост. А.П.
Ляпин. Красноярск, 2001
7.
http://center.fio.ru/som/Resources/Karpuhina/
2003/10/pedsovet
8. http://arbuz.uz/x_stati.html