Многоугольники, описанные около окружности. Геометрия, 8 класс

1. Многоугольники, описанные около окружности

Геометрия, 8 класс, УМК Смирнова И.М.
Иушина А.А., учитель математики
Тасеево, МБОУ «Тасеевская СОШ №2»,
2016г

2. Вставьте пропущенные слова

1. Многоугольник называется описанным
около окружности если…
2. Окружность при этом называется…
3. В любой треугольник можно …
4. Ее центром будет точка пересечения …
5. В любой … многоугольник можно ...
6. Если суммы … сторон четырехугольника
…, то в него можно ...

3. Проверка

1. Многоугольник называется описанным
около окружности если все его стороны
касаются окружности
2. Окружность при этом называется
вписанной
3. В любой треугольник можно вписать
окружность
4. Ее центром будет точка пересечения
биссектрис этого треугольника
5. В любой правильный многоугольник
можно вписать окружность
6. Если суммы противоположных сторон
четырехугольника равны, то в него
можно вписать окружность

4.

5.

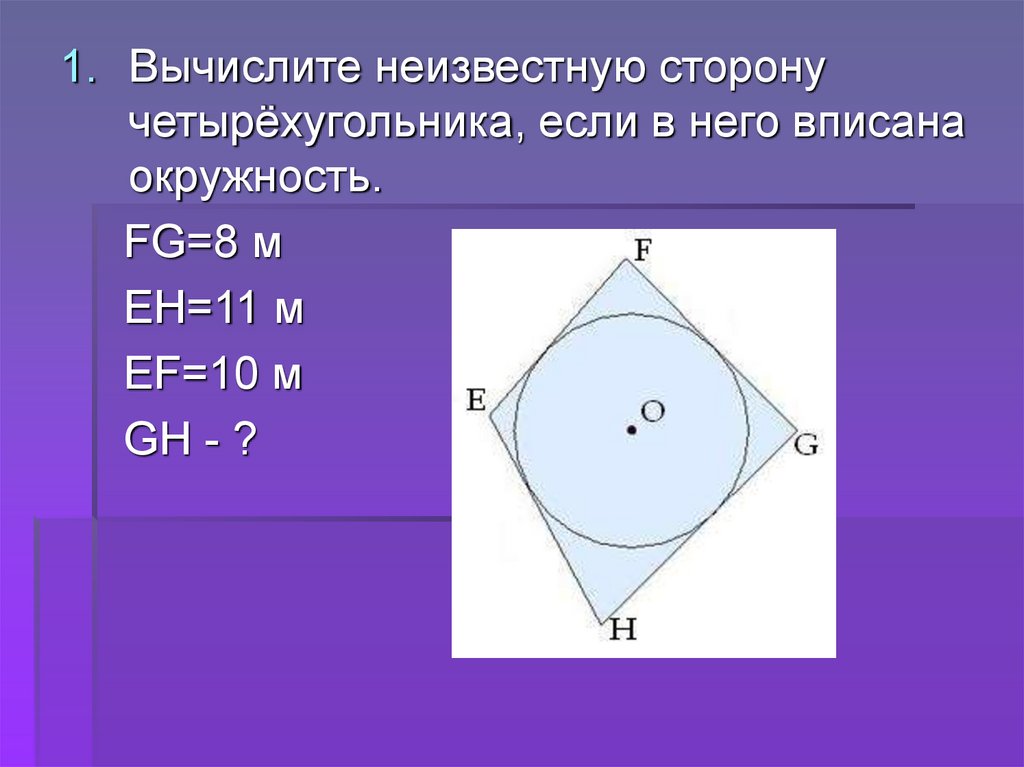
1. Вычислите неизвестную сторону
четырёхугольника, если в него вписана
окружность.
FG=8 м
EH=11 м
EF=10 м
GH - ?

6.

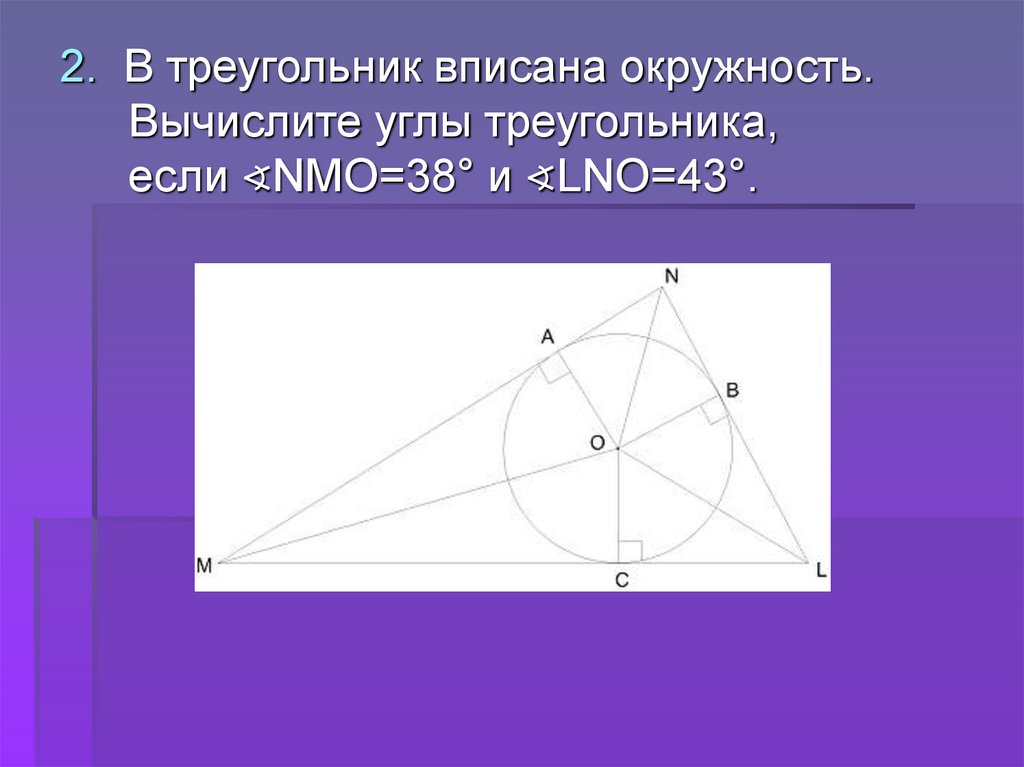
2. В треугольник вписана окружность.
Вычислите углы треугольника,
если ∢NMO=38° и ∢LNO=43°.

7.

3. В треугольник вписана окружность.
Вычислите ∢COA, ∢AOB, ∢BOC,
если ∢NMO=34° и ∢LNO=37°.

8.

4. В прямоугольный
треугольник ABC вписана окружность,
угол B — прямой. Вычислите углы
треугольника A и C, а также углы DOE и
DOF, если ∢FOE=143°.

9.

5. Окружность,
вписанная в
треугольник LMN,
точками касания с
треугольником
делится на дуги,
градусные меры
которых равны:
AB=108° и BC=118°.
Вычислите углы
треугольника и
градусную меру
дуги CA.