Трапеция

1.

Давайте вспомним
определение, свойства и
признаки параллелограмма
Опрос
2

2.

Биссектриса тупого угла параллелограмма
делит
противоположную
сторону
в отношении 3 : 4, считая от вершины
тупого угла. Найдите большую сторону
параллелограмма, если его периметр равен
88.
Ответ: 28.
3

3.

Кроссворд
4

4. Кроссворд

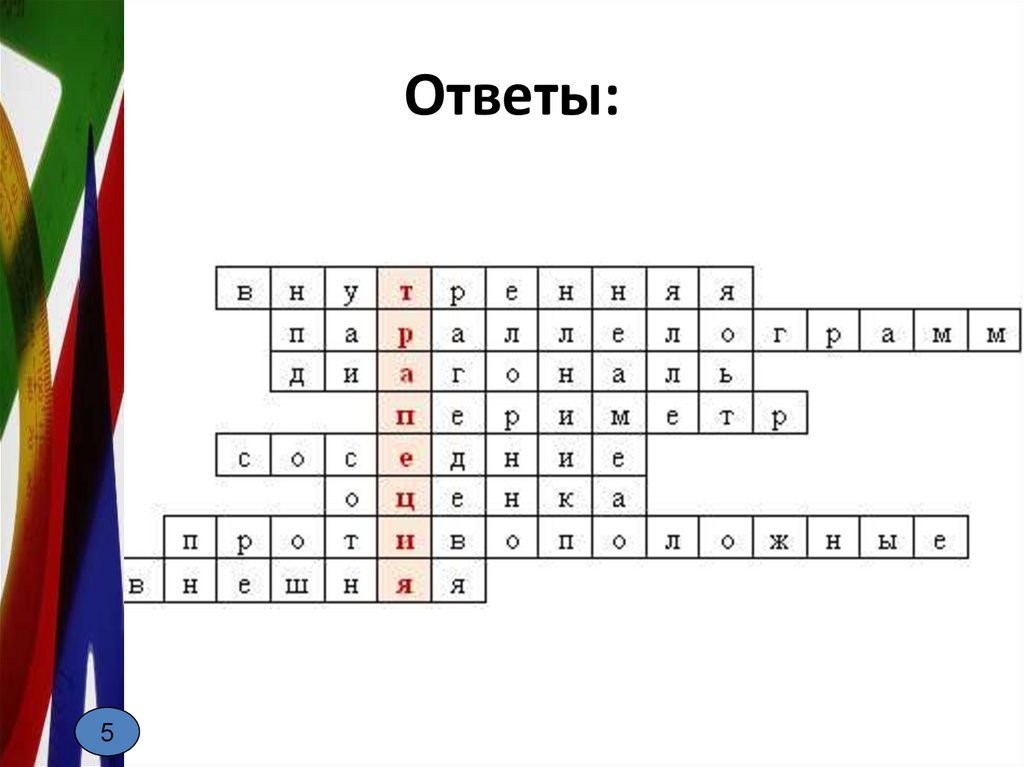
Ответы:
5

5. Ответы:

В
А
6
С
D

6.

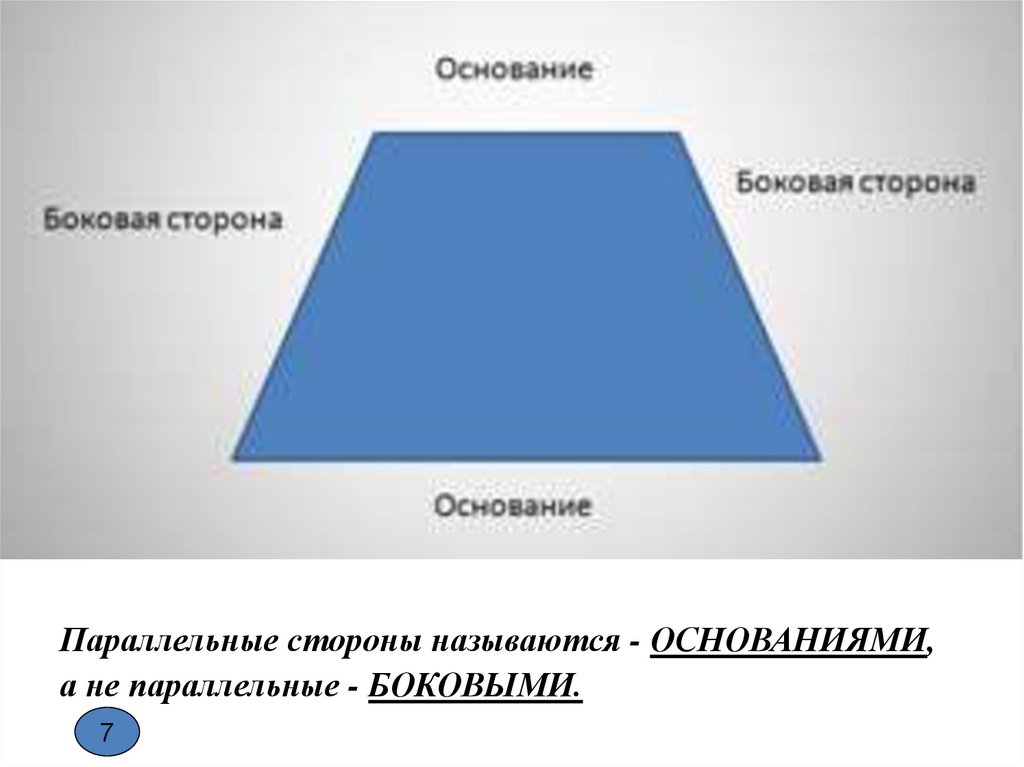
Параллельные стороны называются - ОСНОВАНИЯМИ,
а не параллельные - БОКОВЫМИ.
7

7.

Геометрическая фигура была названа
так по внешнему сходству с
маленьким столом.
23.03.2019
8
С.А. Абрамкина

8.

Немного из
истории
По-гречески "trapedza" значило
"стол", "trapezion" - "столик".
Из второго слова создалось наше
"трапеция" - известная
математическая фигура с двумя
параллельными и двумя не
параллельными сторонами: именно
такой формы столы бывали в
Греции.
9
Первое – " стол", за которым
вкушали пищу монахи
византийских монастырей, - начало
обозначать и сам этот процесс, еду –
«трапезу».

9.

Над этим
приморским
городом высится
гора,
принадлежащая к
типу "столовых".
Основателями
Трапезунда были
греки; они и дали
ему такое
имя: "Город
столовой горы".
10
Город Трапезунд
Столовая гора –
гора с усечённой, плоской вершиной.

10.

Какие четырехугольники на рисунке
являются трапециями? Назовите их
основания и боковые стороны.
P
В
С
700
S
А
1100
700
М
С
В
А
11
B1
С1
D
О
H
N
T
R

11.

Свойство углов трапеции
12

12. Свойство углов трапеции

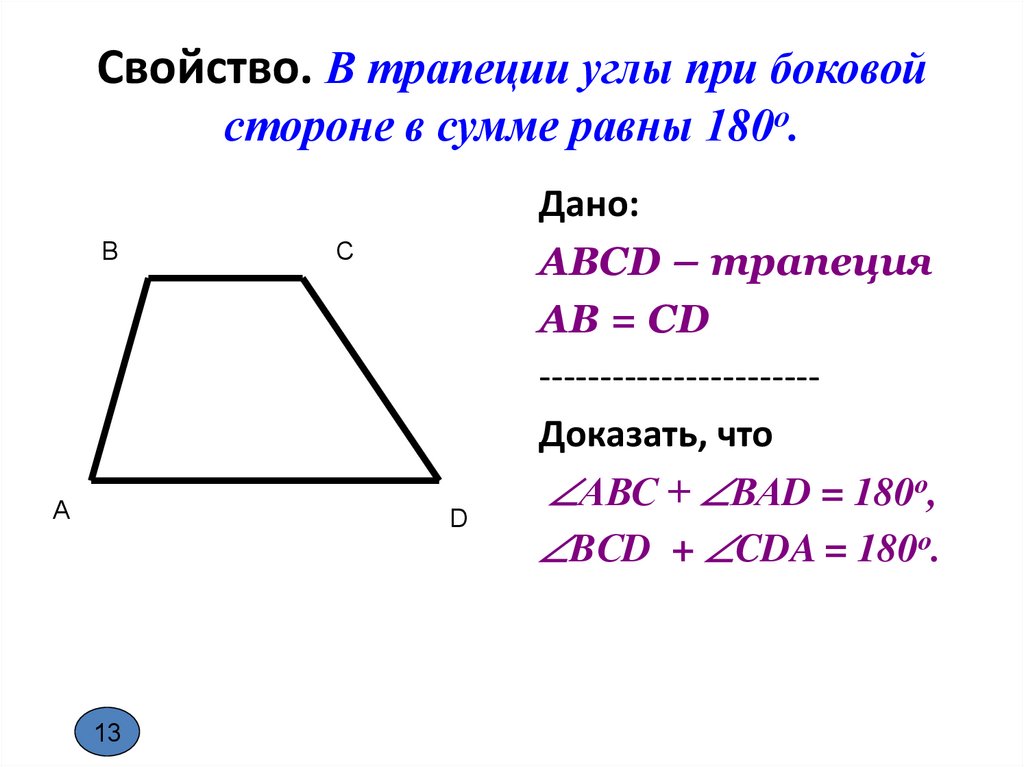
Свойство. В трапеции углы при боковой
стороне в сумме равны 180о.
В
А
С
D
13
Дано:
АВСD – трапеция
АВ = CD
----------------------Доказать, что
АВС + ВАD = 180о,
BСD + CDA = 180о.

13. Свойство. В трапеции углы при боковой стороне в сумме равны 180о.

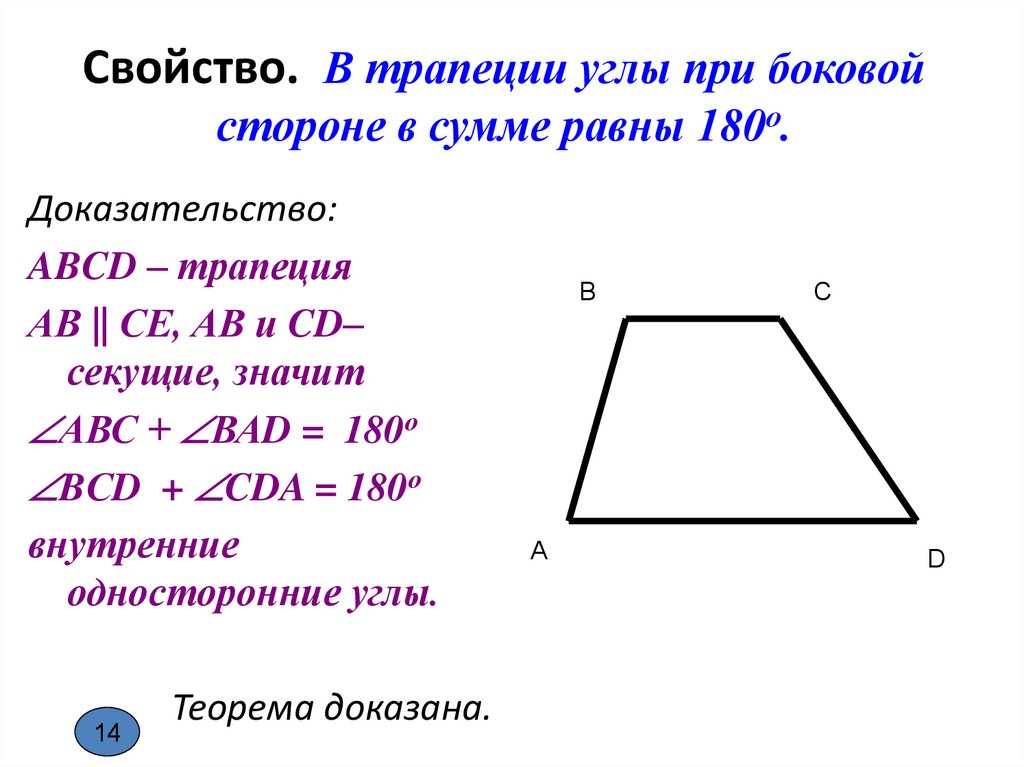
Свойство. В трапеции углы при боковой
стороне в сумме равны 180о.
Доказательство:
ABCD – трапеция
АВ || СЕ, АВ и CD–
секущие, значит
АВС + ВАD = 180о
BСD + CDA = 180о
внутренние
односторонние углы.
14
Теорема доказана.
В
А
С
D

14. Свойство.  В трапеции углы при боковой стороне в сумме равны 180о.

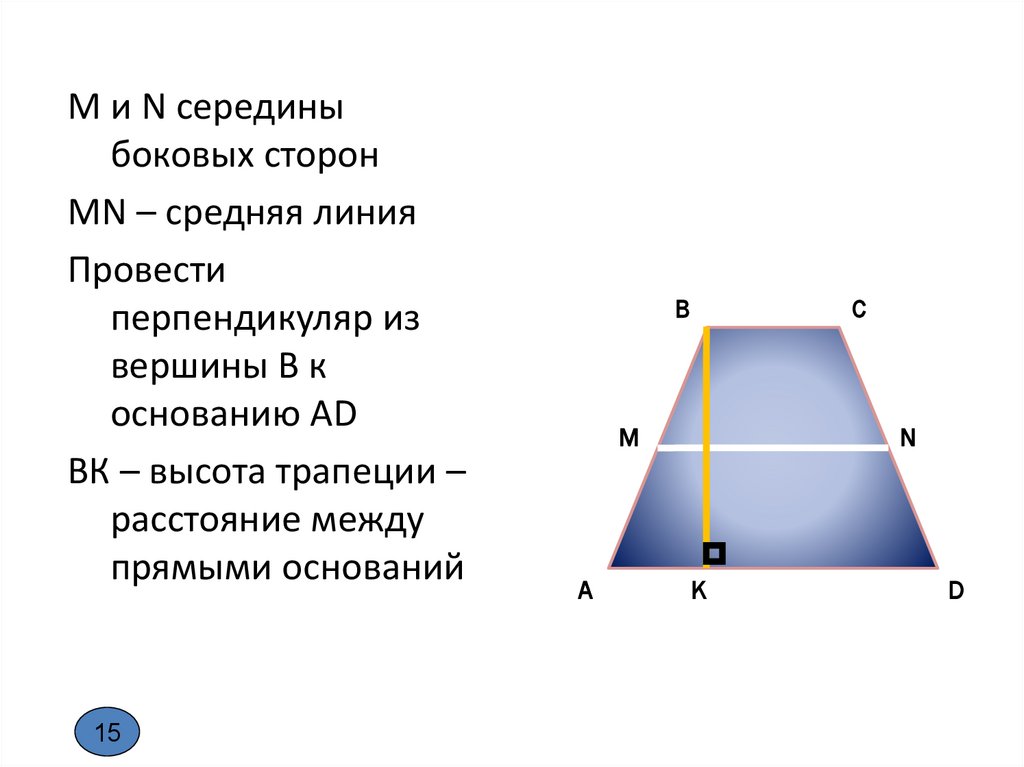
М и N середины
боковых сторон
MN – средняя линия
Провести
перпендикуляр из
вершины В к
основанию AD
ВК – высота трапеции –
расстояние между
прямыми оснований
15
В
С
M
А
N
K
D

15.

16
Равнобедренная –
трапеция, у которой равны боковые стороны.

16.

Прямоугольная –
трапеция, один из углов которой прямой.
17

17.

• 1 ряд - исследуют диагонали
равнобедренной трапеции.
• 2 ряд – исследуют углы равнобедренной
трапеции.
18

18.

Смотрите внимательно на рисунок в течении 30 секунд
19

19.

20

20.

Свойства равнобедренной
трапеции.
• В равнобедренной трапеции углы при каждом
основании равны.
21

21. Свойства равнобедренной трапеции.

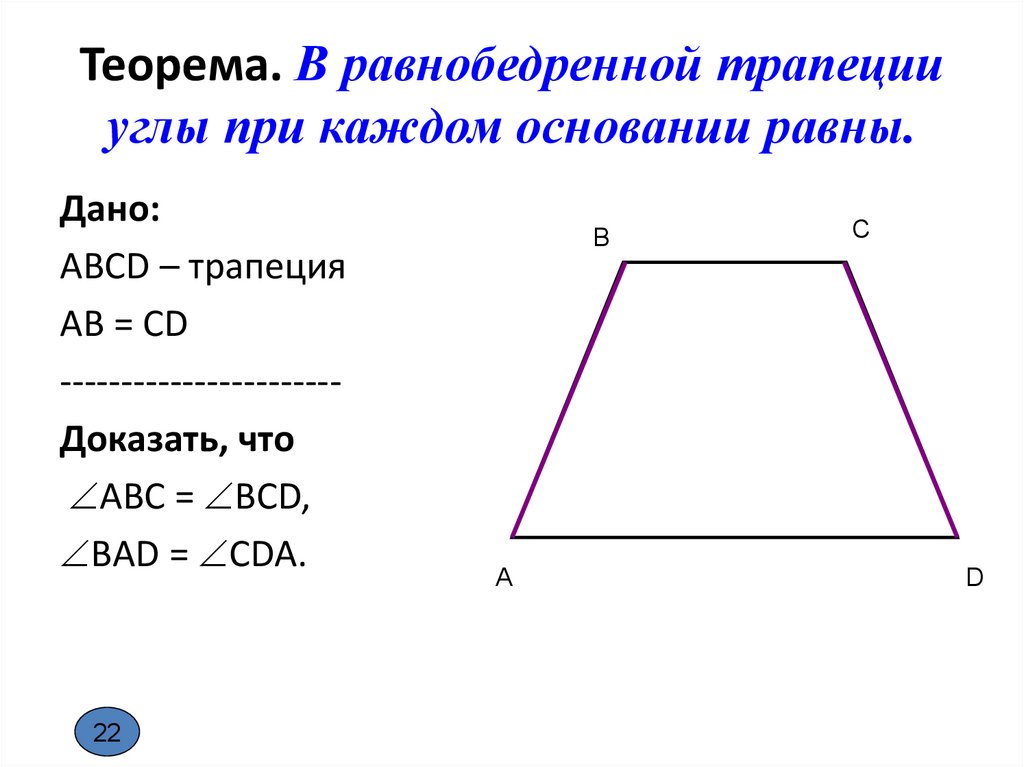
Теорема. В равнобедренной трапеции
углы при каждом основании равны.
Дано:
АВСD – трапеция
АВ = CD
----------------------Доказать, что
АВС = ВСD,
BАD = CDA.
22
В
А
С
D

22. Теорема. В равнобедренной трапеции углы при каждом основании равны.

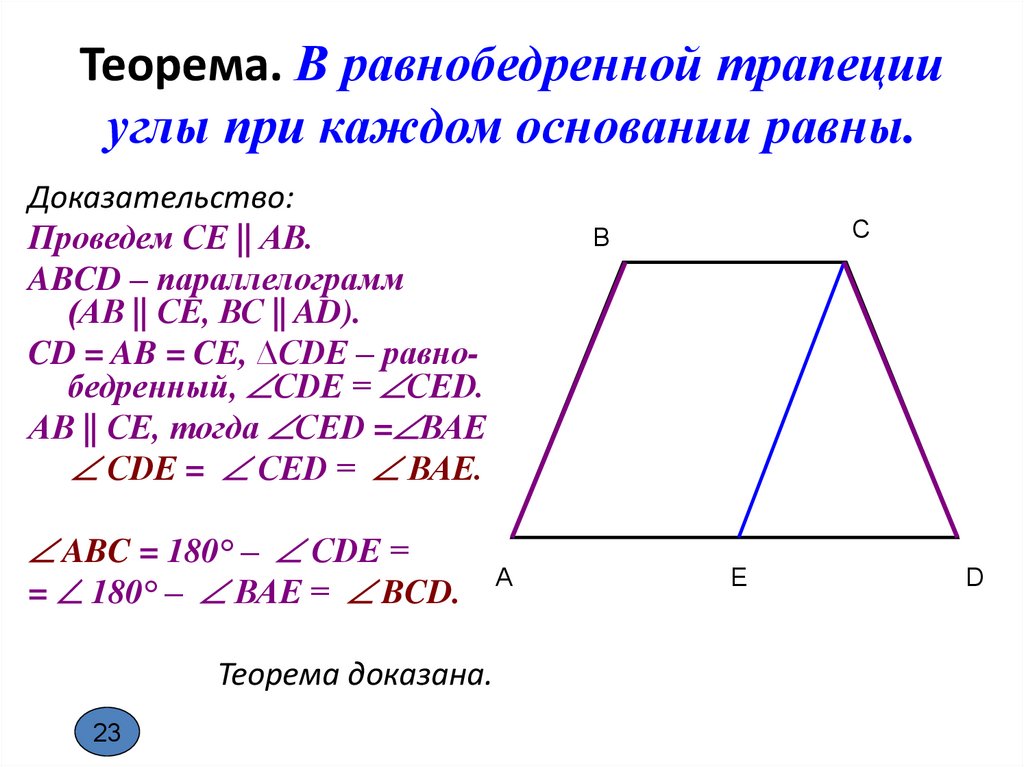
Теорема. В равнобедренной трапеции
углы при каждом основании равны.
Доказательство:
Проведем СЕ || АВ.
ABCD – параллелограмм
(АВ || СЕ, ВС || AD).
CD = AB = CE, ∆СDE – равнобедренный, СDЕ = СЕD.
АВ || СЕ, тогда СЕD = ВАЕ
СDЕ = СЕD = ВАЕ.
ABC = 180° – СDЕ =
= 180° – ВАЕ = BCD.
Теорема доказана.
23
С
В
А
E
D

23. Теорема. В равнобедренной трапеции углы при каждом основании равны.

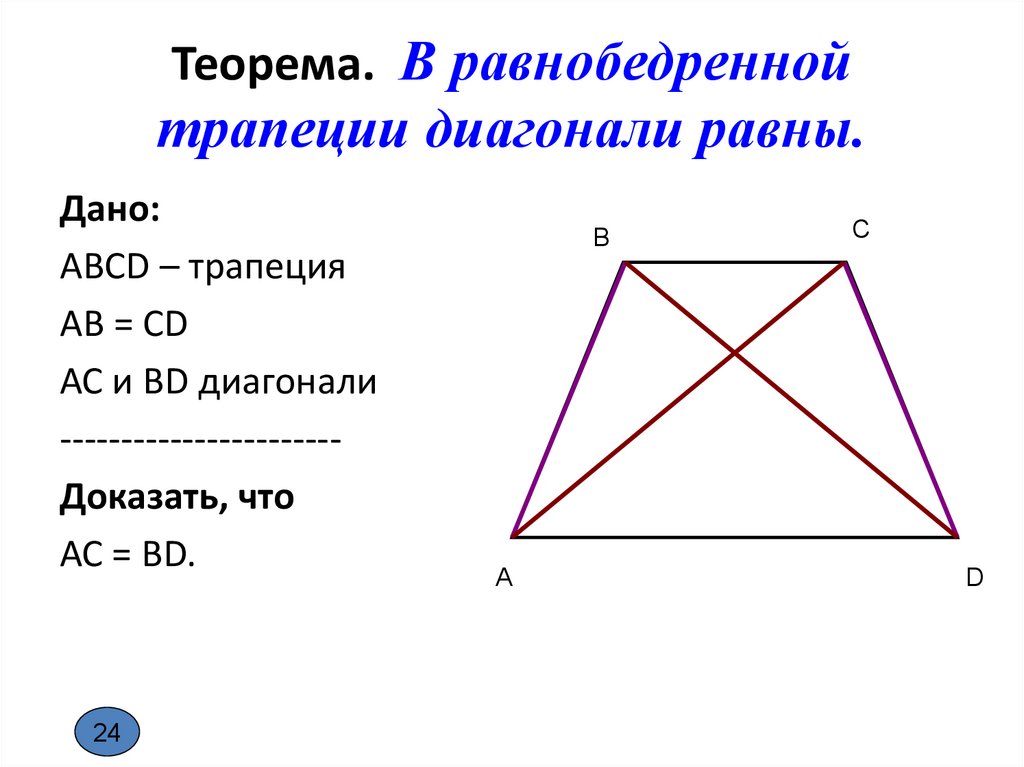
Теорема. В равнобедренной
трапеции диагонали равны.
Дано:
АВСD – трапеция
АВ = CD
АС и BD диагонали
----------------------Доказать, что
АС = BD.
24
В
А
С
D

24. Теорема.  В равнобедренной трапеции диагонали равны.

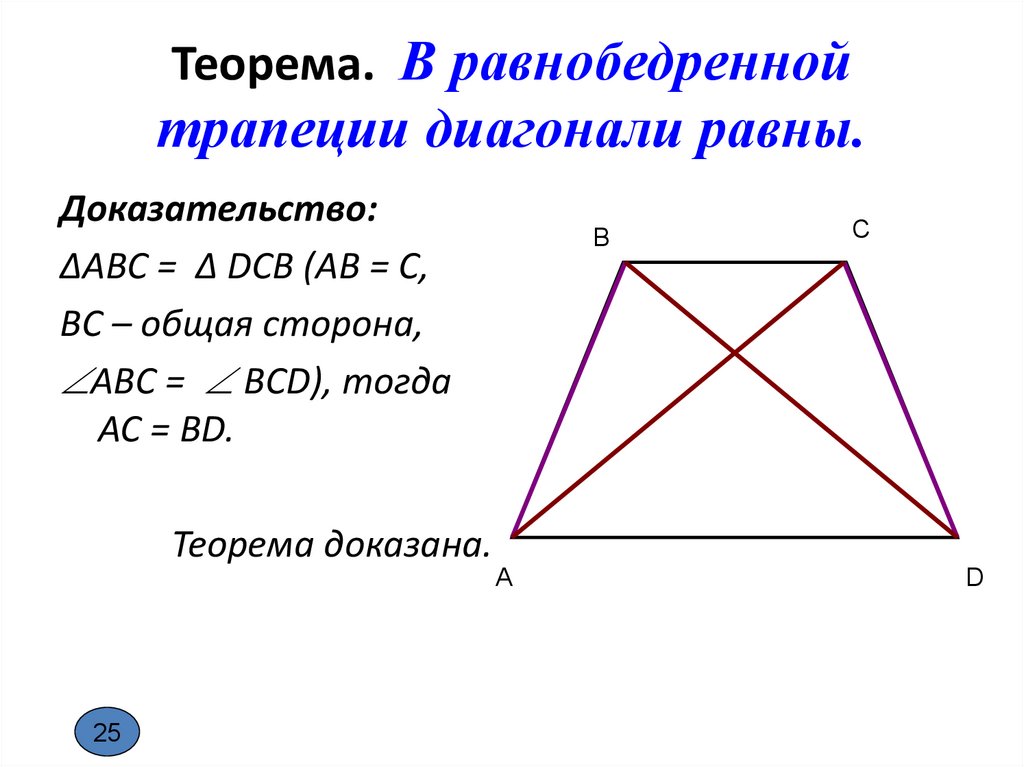
Теорема. В равнобедренной
трапеции диагонали равны.
Доказательство:
∆ABC = ∆ DСВ (АВ = С,
ВС – общая сторона,
АВС = ВСD), тогда
АС = ВD.
Теорема доказана.
25
В
А
С
D

25. Теорема.  В равнобедренной трапеции диагонали равны.

Сформулируйте
утверждения, обратные
свойствам.
26

26. Сформулируйте утверждения, обратные свойствам.

Признаки равнобедренной
трапеции.
• 1. Если углы при основании трапеции
равны, то она равнобедренная.
• 2. Если диагонали трапеции равны, то она
равнобедренная.
• Доказательство признаков провести
самостоятельно к следующему уроку.
27

27. Признаки равнобедренной трапеции.

Применение формы трапеции
в повседневной жизни
• в интерьерах (диваны, стены, навесные
потолки);
• в ландшафтном дизайне (границы газонов,
искусственных водоемов, формы камней);
• в индустрии моды (одежда, обувь, аксессуары);
•в
дизайне
предметов
повседневного
пользования (светильники, чайники, пылесосы с
использованием форм трапеции и т.д.);
• в архитектуре
28
15

28.

Интерьер
29

29.

Ландшафтный дизайн
30

30.

Архитектура
31

31.

Одежда, аксессуары
32

32.

Бытовые предметы
33

33.

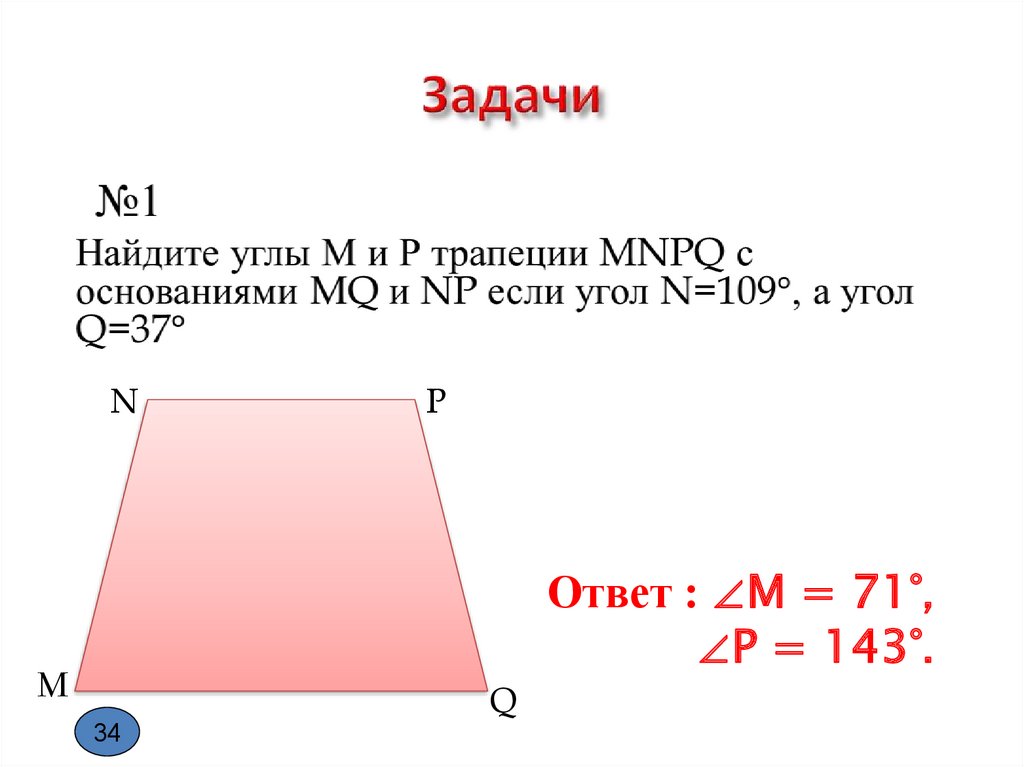
N
P
Ответ : ∠M = 71°,
∠P = 143°.
M
Q
34

34.

B
C
D
A
35
Ответ: 115°, 65°,65°

35.

B
C
D
A
36
Ответ : 22 см.

36.

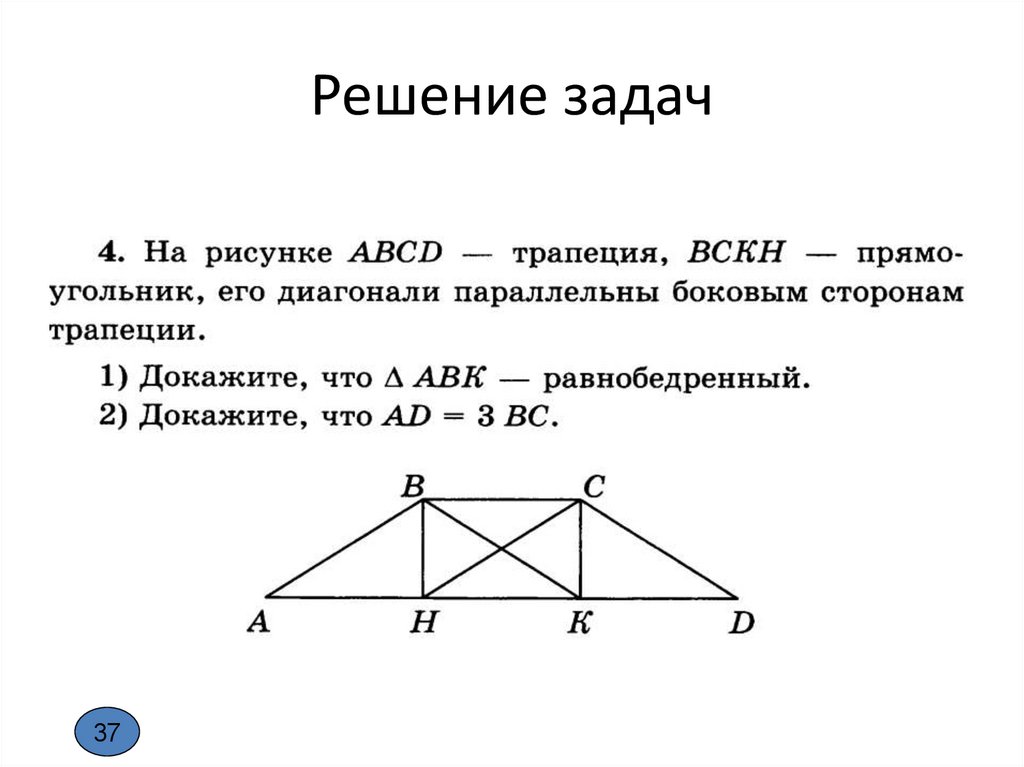
Решение задач
37

37. Решение задач

38

38.

39

39.

1. Какой четырехугольник называется
трапецией?
Как называются стороны трапеции?
2. Какие существуют виды трапеций?
3. Какими свойствами обладает
равнобедренная трапеция?
40

40.

41