Похожие презентации:
Методы измерения информации
1. Методы измерения информации
2.
Кто владеет информацией,тот владеет миром.
Френсис Бэкон
Процесс познания окружающего мира
приводит к накоплению информации в
виде знаний.
Получение информации приводит к
расширению знаний, т.е., к
уменьшению неопределённости
нашего знания.
2
3.
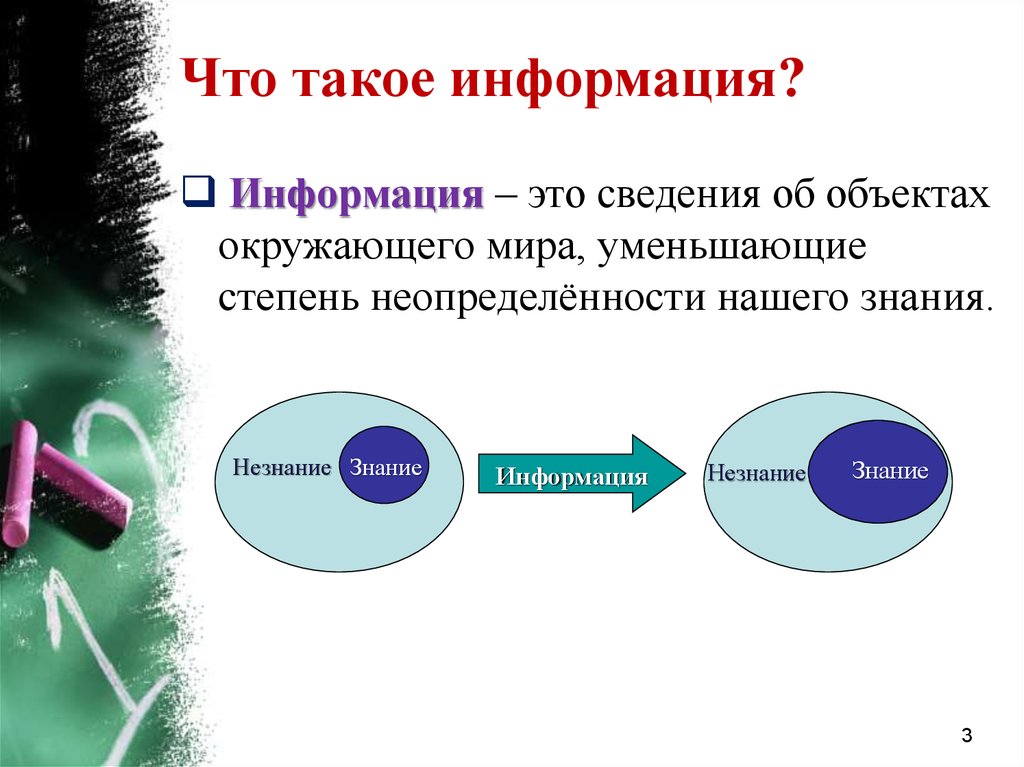
Что такое информация?Информация – это сведения об объектах
окружающего мира, уменьшающие
степень неопределённости нашего знания.
Незнание Знание
Информация
Незнание
Знание
3
4.
Как можно измеритьинформацию?
Существует два подхода к измерению
информации:
1) алфавитный (количество информации
в тексте определяется независимо от его
содержания, воспринимая текст как
последовательность символов);
2) содержательный или вероятностный
(количество информации в тексте
связывается с содержанием текста,
учитывая вероятности его символов).
4
5.
Основные определенияАлфавит – это множество
символов, используемых при
записи текста.
Мощность алфавита –
это количество символов
алфавита.
Информационный вес
одного символа – это
количество информации в
одном символе.
Информационный вес символа двоичного
алфавита принят за единицу измерения
информации и называется 1 бит.
5
6. Алфавитный подход
Впервые информацию измериламериканский инженер Ральф
Хартли в 1928 году.
Р. Хартли предполагал, что
появление символов в сообщении длины l
равновероятно, т.е., ни один из символов
не имеет преимущества перед другими
символами,
мощность алфавита равна s .
Вопрос: чему равно количество
информации в сообщении?
6
7.
Формула ХартлиИнтересно знать, что логарифм
(log) – это единственная
функция f , удовлетворяющая
условию
l
f (s ) l f (s).
Каждый символ сообщения имеет S
возможностей выбора.
Следовательно, сообщение длины l имеет
S l возможностей выбора.
Тогда количество информации (в битах) I
в сообщении длины l равно
I log 2 ( S l ) l log 2 ( S ).
7
8.
Алфавитный подход: поясненияКаждый символ сообщения содержит
log 2 (S ) информации.
Следовательно, сообщение длины l
должно содержать в l раз больше
информации, т.е., l log 2 (S ) информации.
8
9.
Алфавитный подход: примерыЗадача 1: Монета с двумя
сторонами (названными
«Орёл» и «Решка»)
бросается вверх. Чему равно
количество информации в
сообщении о том, что
стороной вверх выпала
«Решка»?
Решение:
N=2
l =1
I =?
I 1 log 2 (2) 1 бит.
Ответ: 1 бит.
9
10.
Алфавитный подход: примерыЗадача 2: Бросается
шестигранный игральный
кубик, на гранях которого
написаны числа 1 – 6.
Вычислить количество
информации в сообщении о
том, что стороной вверх
выпала сторона с числом 1.
Решение:
N=6
l =1
I =?
I log 2 (6) 2.585 бит.
Ответ: I 2.585 бит.
10
11.
Алфавитный подход: примерыЗадача 3: Сообщение,
записанное символами
алфавита мощности 32,
содержит 80 символов.
Чему равно количество
информации в сообщении?
Решение:
S = 32
l = 80
I =?
I 80 log 2 (32)
80 5 400 бит.
Ответ: I 400 бит.
11
12.
Вероятностный подходСуществует множество ситуаций,
когда возможные события имеют
различные вероятности реализации.
Пример 1: Если в ящике белых шаров
больше, чем чёрных, то вероятнее взять
белый шар, чем чёрный.
Пример 2: Когда сообщают прогноз
погоды, то сообщение о том, что будет
дождь, более вероятно летом, а
сообщение о снеге – зимой.
12
13.
Вероятностный подходАмериканский инженер и математик Клод
Шеннон в 1948 году в статье «Математическая
теория связи» предложил формулу для
измерения количества информации в случае
различных вероятностей событий.
13
14.
К. Шеннон является основателем теорииинформации.
К. Шеннон первым предложил использовать
термин «бит» для обозначения наименьшей
единицы измерения информации.
14
15.
Классическое определениевероятности
Вероятность p случайного события
равна отношению числа исходов k ,
благоприятствующих данному событию,
к общему числу S равновозможных
исходов:
k
p .
S
15
16.
Вероятностный подходК. Шеннон ввёл количество
информации (в битах) I ( рi )
i-ого символа алфавита
следующим образом:
1
I ( рi ) log 2 log 2 pi ,
pi
где pi - вероятность появления i-го символа
алфавита.
Величина I ( рi ) называется собственной
информацией i-ого символа алфавита.
16
17.
Собственная информацияЗамечание: Чем меньше
вероятность i-ого символа
алфавита, тем больше его
собственная информация.
В задаче 2 (с бросанием
шестигранного игрального
кубика) полученная информация
больше, чем в задаче 1 (с
бросанием монеты с двумя
сторонами).
Следовательно, чем меньше мы
знаем о сообщении, тем больше
информации в ней содержится.
17
18.
Формула ШеннонаК. Шеннон рассмотрел также
среднее количество информации в
сообщении, которую назвал
информационной энтропией.
Информационная энтропия Н равна
H p1 I ( p1 ) p2 I ( p2 ) ... pS I ( pS )
S
pi log 2 pi .
i 1
18
19.
История понятияэнтропии
Понятие энтропии впервые было
введено немецким физиком Р.
Клаузиусом в термодинамике в
1865 году.
Австрийский физик Л. Больцман и
американский физик У. Гиббс
связали энтропию с вероятностью и
описали термодинамическую
систему с помощью энтропии.
К. Шеннон ввёл понятие энтропии
в теорию информации.
19
20.
Информация это то, что устраняетнеопределённость выбора.
Клод Шеннон
Информационная энтропия
– мера хаотичности
информации, определяющей
неопределенность появления
символа в сообщении.
Информационная энтропия
принимает своё максимальное
значение (H log 2 (S )) при
равновероятных символах,
т.е., p1 p2 pS 1 / S .
20
21.
Связь формул Шеннона и ХартлиВ частном случае, когда все символы в
сообщении равновероятны:
p1 p2 pS 1 / S ,
формула Шеннона совпадает с формулой
Хартли:
S
1
1
H log 2 log 2 S .
S
i 1 S
21
22.
Вероятностный подход: примерыЗадача 4: В корзине лежат 8 чёрных и 24 белых
шаров. Сколько информации несет сообщение о
том, что достали шар фиксированного цвета?
Сколько информации несет сообщение о том, что
достали шар любого цвета?
Решение: рчёрн 8 / 32 0.125, рбел 24 / 32 0.725.
I ( рчёрн ) log 2 рчёрн log 2 0.125 2 бит,
I ( рбел ) log 2 рбел log 2 0.725 0.415 бит,
H 0.125 log 2 0.125 0.725 log 2 0.725
0.25 0.3009 0.551 бит.
Ответ: I ( рчёрн ) 2 бит, I ( рбел ) 0.415 бит,
H 0.551 бит.
22
23.
Вероятностный подход: примерыЗадача 5: Бросается
несимметричная четырёхгранная
пирамида. Известно, что
p1 0.5, p2 0.25, p3 p4 0.125
являются вероятностями выпадения
граней пирамиды. Вычислить
количество полученной информации о
выпадении какой-то грани пирамиды.
Решение:
H 0.5 log 2 0.5 0.25 log 2 0.25 0.25 log 2 0.125
0.5 2 0.375 2 1.75 бит.
Ответ: H 1.75 бит .
23
24.
ВыводыПри
алфавитном
подходе
измерения
информации предполагается, что все символы
алфавита
встречаются
в
сообщениях,
записанных с помощью этого алфавита,
одинаково часто. Однако в действительности
символы алфавитов в сообщениях появляются с
разной частотой.
При
вероятностном
подходе
измерения
информации
количество
информации
в
сообщении о некотором событии зависит от
вероятности этого события. Чем меньше
вероятность некоторого события, тем больше
информации содержит сообщение об этом
событии. Среднее количество информации
достигает
максимального
значения
при
равновероятных событиях.
24
25.
Литература1. Информатика и ИКТ. Учебник. 10 класс / Под
ред. Проф. Н.В. Макаровой. - СПб.: Питер,
2013.
2. Работы по теории информации и кибернетике.
/ Шеннон К. — М.: Изд-во иностранной
литературы, 1963.
3. http://festival.1september.ru/articles/572186/
25
























 Информатика
Информатика