Пирамида. Теорема о площади боковой поверхности правильной пирамиды

1. Пирамида

2.

Цели и задачи:
1. Ввести понятие пирамиды
2. Доказать теорему о площади боковой
поверхности правильной пирамиды
3. Рассмотреть задачи, связанные с
пирамидой.

3. План

1.
2.
3.
4.
5.
Определение пирамиды
Элементы пирамиды
Правильная пирамида
Площадь поверхности пирамиды
Решение задач: 1, 2, 3

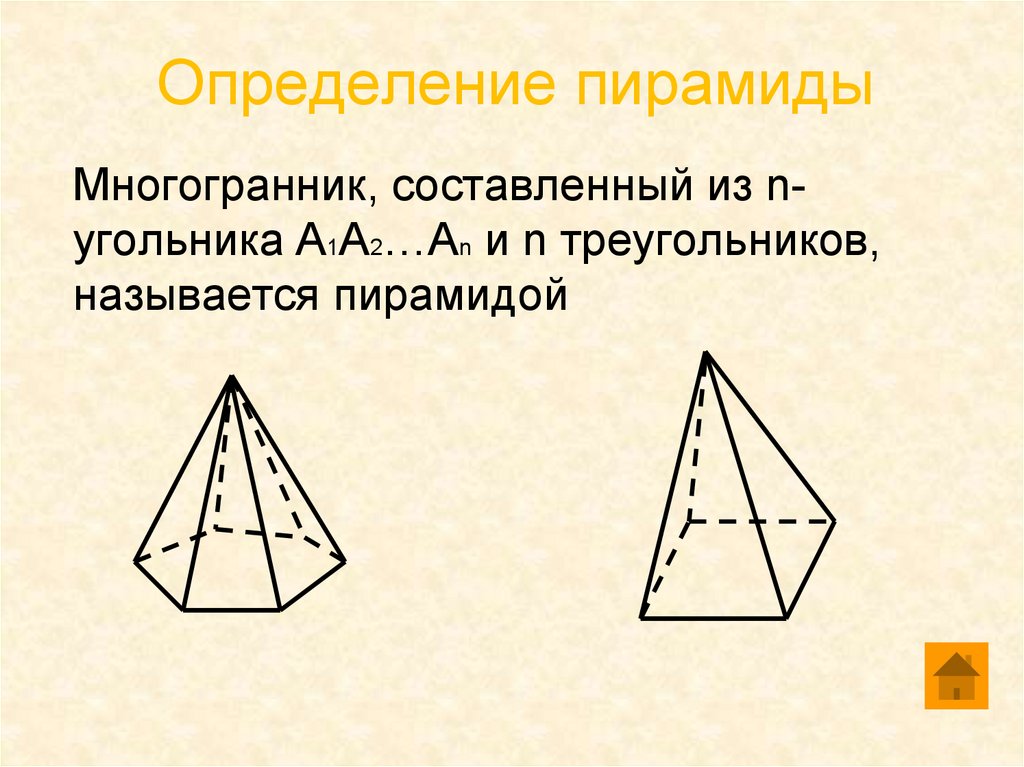
4. Определение пирамиды

Многогранник, составленный из nугольника А1А2…Аn и n треугольников,
называется пирамидой

5. Элементы пирамиды

Многоугольник А1А2...Аn - основание.
Треугольники - боковые грани
Точка Р – вершина пирамиды
Отрезки РА1, РА2,…РАn –
боковые ребра пирамиды
Перпендикуляр, проведенный из
вершины пирамиды к основанию,
называется
высотой пирамиды
p
a
An
H
A1
A2
A3

6.

Правильная пирамида
Пирамида называется правильной, если ее основание – правильный
многоугольник, а отрезок PO, соединяющий вершину пирамиды P с
центром основания, является ее высотой
p
центр
основания
h
An
Высота боковой грани
правильной пирамиды,
проведенная из ее
вершины Р, называется
A1
апофемой РЕ
O
основание –
правильный
многоугольник
Е
A2

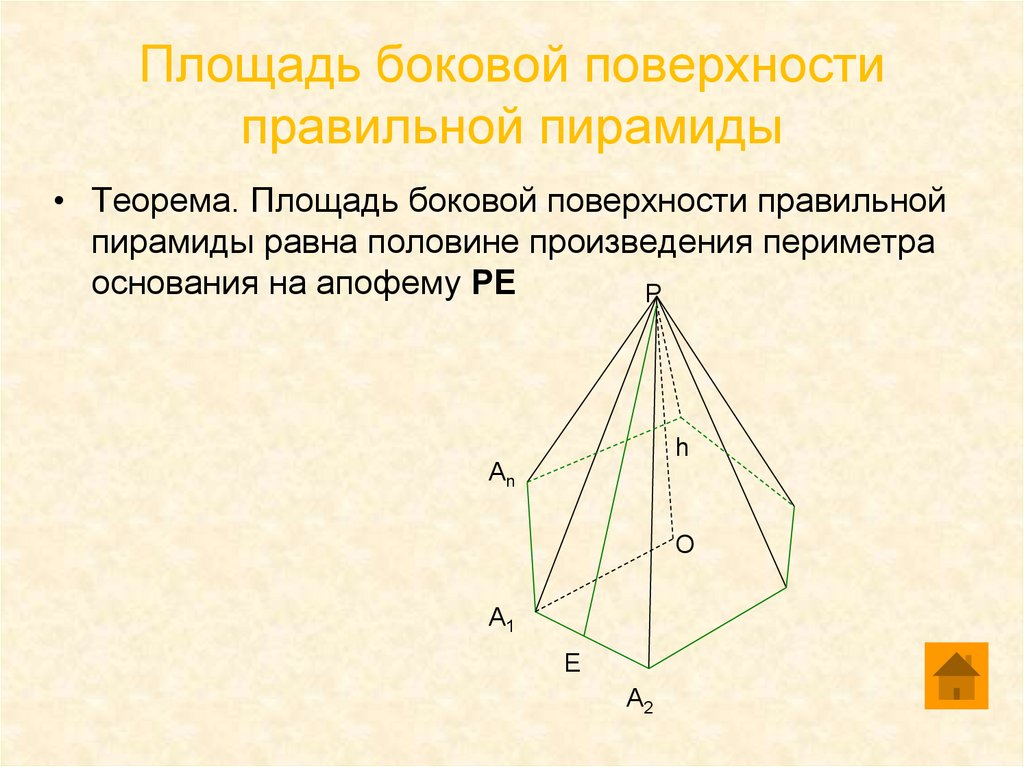
7. Площадь боковой поверхности правильной пирамиды

• Теорема. Площадь боковой поверхности правильной
пирамиды равна половине произведения периметра
основания на апофему РЕ
Р
h
An
O
A1
Е
A2

8.

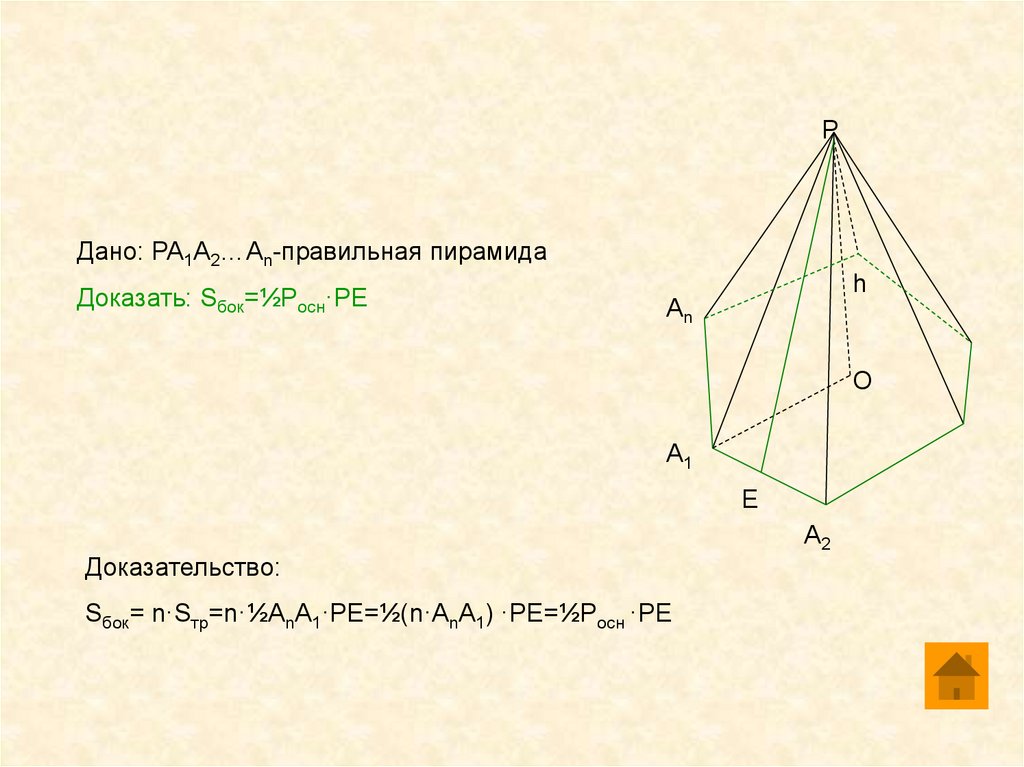
Р
Дано: PA1A2…An-правильная пирамида
Доказать: Sбок=½Pocн·PE
h
An
O
A1
Е
Доказательство:
Sбок= n·Sтр=n·½AnA1·PE=½(n·AnA1) ·PE=½Pосн ·PE
A2

9. Площадь полной поверхности пирамиды

•Площадью полной поверхности пирамиды
называется сумма площадей всех ее
граней (т. е. основания и боковых граней) , а
площадью боковой поверхности пирамиды –
сумма площадей граней
•S
полн
=S + S
бок
осн

10.

Решение задач
Задача 1. Основанием пирамиды является параллелограмм со
сторонами 5м и 4м и меньшей диагональю 3м. Высота пирамиды
проходит через точку пересечения диагоналей основания и равна2м.
Найдите площадь поверхности пирамиды.
M
D
С
O
А
K
F
В

11.

Решение:
Треугольник ABD –прямоугольный (42+32=52)
M
Угол ADB равен 900.
1) AD и DO перпендикулярны, DO –
проекция МD на АВС, следовательно
AD и MD перпендикулярны
( по теореме о трех перпендикулярах)
Следовательно MD высота ∆MAD.
С
D
2) ∆MDO: MD=√22+1,52=2,5
3)∆ADB: DK и AB перпендикулярны,
рассмотрим SADB:
AB·DK=AD·BD,DK=2,4м
∆MOF: OF║DK, OF= ½DK, OF= 1,2.
MF=√MO2+OF2= 0,4√34 .
O
А
K
Sбок= 2SAMD+2SAMB=4·2,5+5·0,4·√34=10+2 √34
Sосн=4·3=12
Sпир=(22+2 √34)м2.
F
В

12.

Задача 2. Основанием пирамиды DABC является ∆АВС,
у которого АВ=АС=13см, ВС=10см. Ребро АD перпендикулярно
к плоскости основания и равно 9см. Найти площадь боковой
поверхности пирамиды.
D
С
А
В

13.

Решение:
1) Проведем АК перпендикулярно ВС
D
ВС и DK перпендикулярны (по
теореме о трех перпендикулярах)
DK – высота ∆DBC.
2) ∆АВК: АК = √АВ2-BK2=√144=12см
3) ∆DAK: DK=15см
4) ∆ADB = ADC (по двум катетам)
Sбок= 2SADB+SBDC
Sбок=2·½·13·9+½·10 ·15 = 192см2.
С
А
К
В

14.

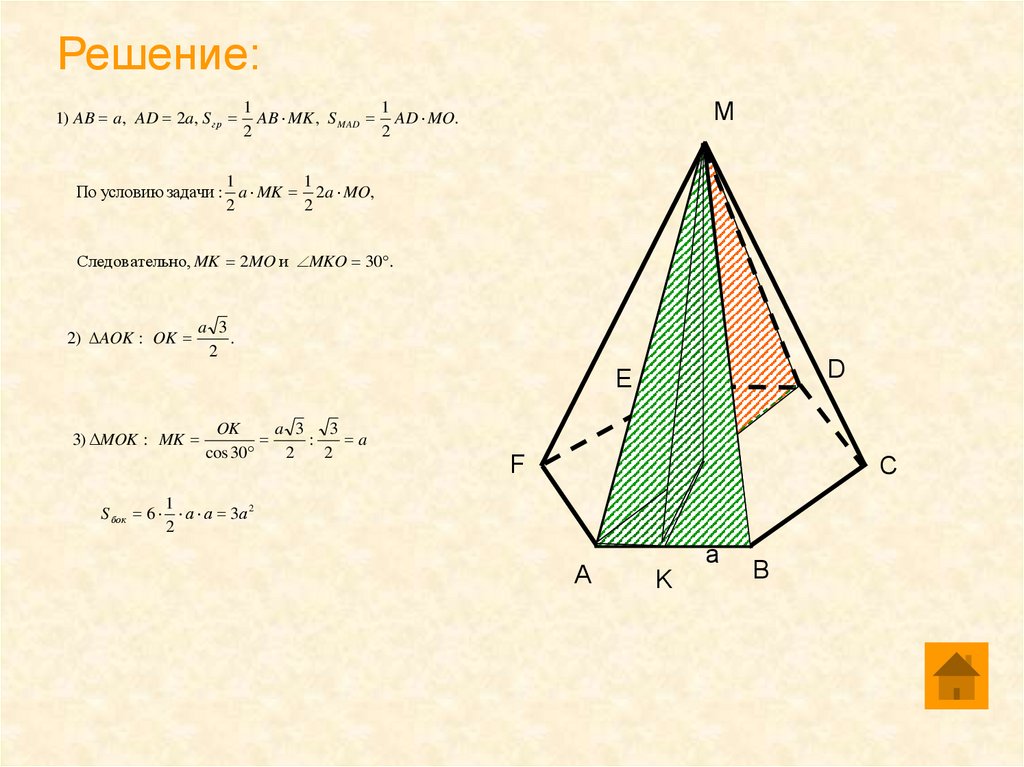
Задача 3.
Найдите площадь боковой поверхности правильной шестиугольной
пирамиды, если сторона ее основания равна а, а площадь боковой грани
равна площади сечения, проведенного через вершину пирамиды и
большую диагональ основания
M
D
E
F
C
O
A
a
K
B

15.

Решение:
1) AB a, AD 2a, S гр
1
1
AB MK , S MAD AD MO.
2
2
M
1
1
По условию задачи : a MK 2a MO,
2
2
Следовательно, MK 2MO и MKO 30 .
2) AOK : OK
a 3
.
2
D
E
3) ΔMOK : MK
OK
a 3
3
:
a
cos 30
2
2
F
C
O
1
S бок 6 а а 3а 2
2
A
a
K
B

16.

Домашнее задание:
П. 28, 29, задачи 248, 265
Справочные материалы:
Многогранники
Пирамида