Похожие презентации:
Решение задач оптимизации методом ветвей и границ
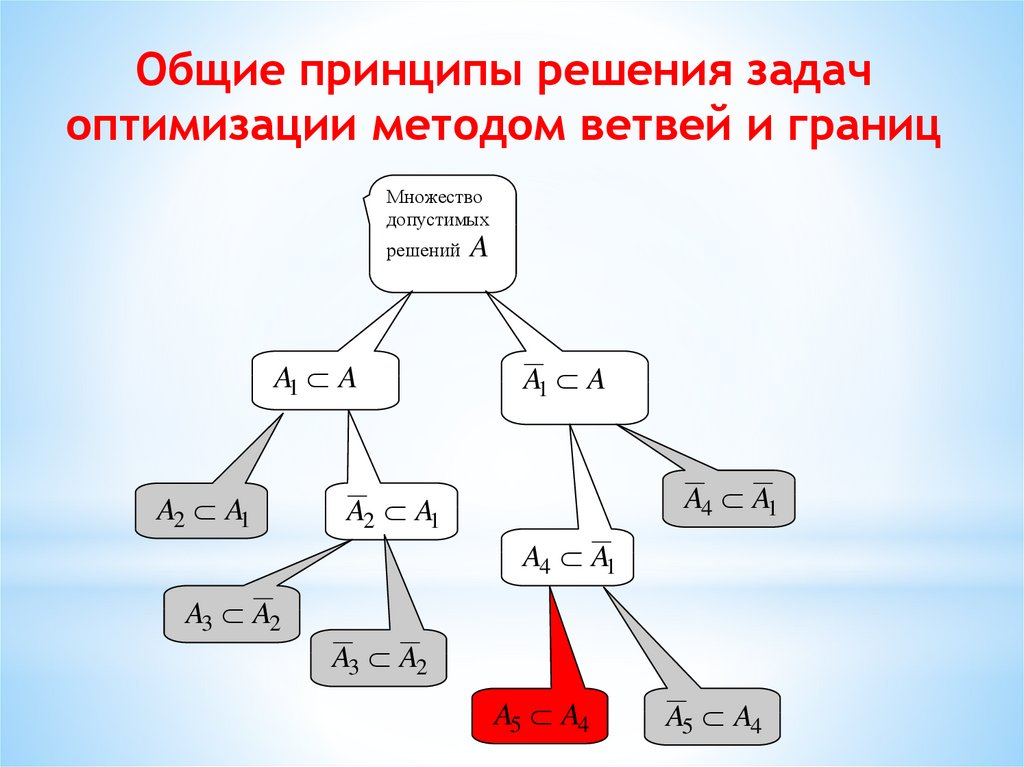
1. Общие принципы решения задач оптимизации методом ветвей и границ
Множестводопустимых
решений
A1 A
A2 A1
A
A1 A
A4 A1
A2 A1
A4 A1
A3 A2
A3 A2
A5 A4
A5 A4
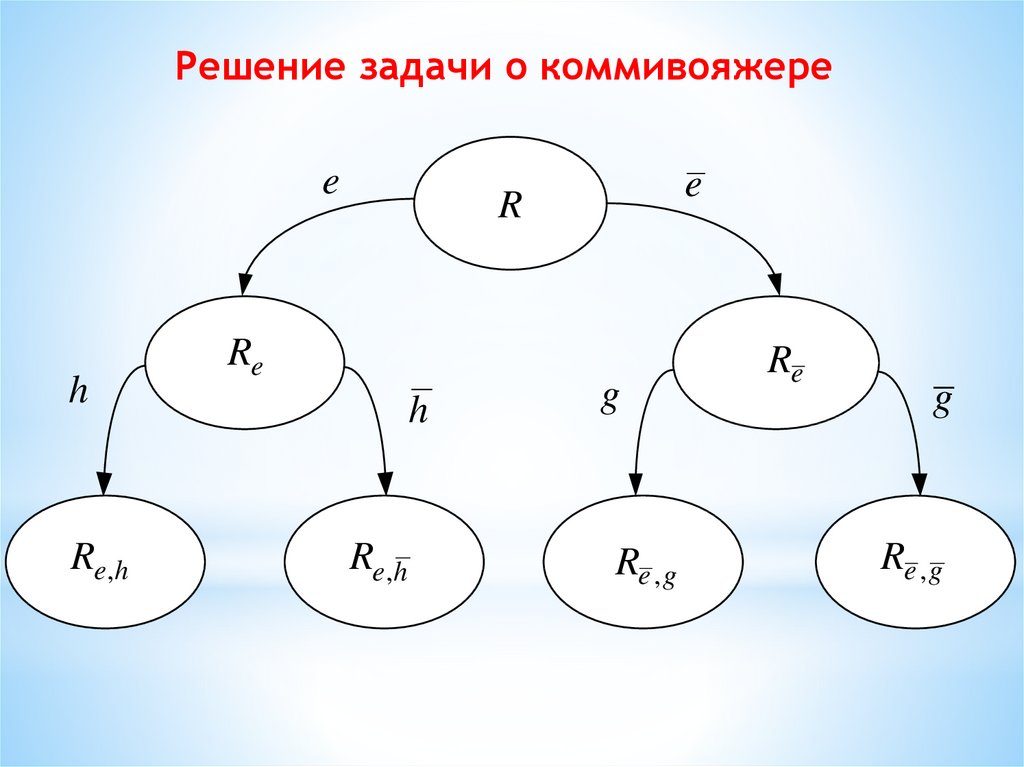
2. Решение задачи о коммивояжере
eh
Re,h
e
R
Re
h
Re,h
g
Re , g
Re
g
Re , g
3.
Утверждение 1. Изменение всех элементов строки матрицырасстояний на одно и то же число не влияет на выбор
оптимального маршрута коммивояжера.
Утверждение 2. Изменение всех элементов столбца матрицы
расстояний на одно и то же число не влияет на выбор
оптимального маршрута коммивояжера.
Если последовательно для каждой вершины v j V графа G (V , E )
|V |
вычислить значения α j и β j , то величина γ (α j β j ) будет
j 1
составляющей веса кратчайшего кольцевого маршрута, но никогда его не
превысит. Другими словами, γ можно использовать как нижнюю границу
веса кратчайшего кольцевого маршрута.
4.
Расстояния между городами, кмГород
1
2
3
4
5
1
2
3
4
5
∞
6
5
1
2
9
∞
3
7
4
8
4
∞
2
5
4
5
6
∞
2
10
7
2
8
∞
5.
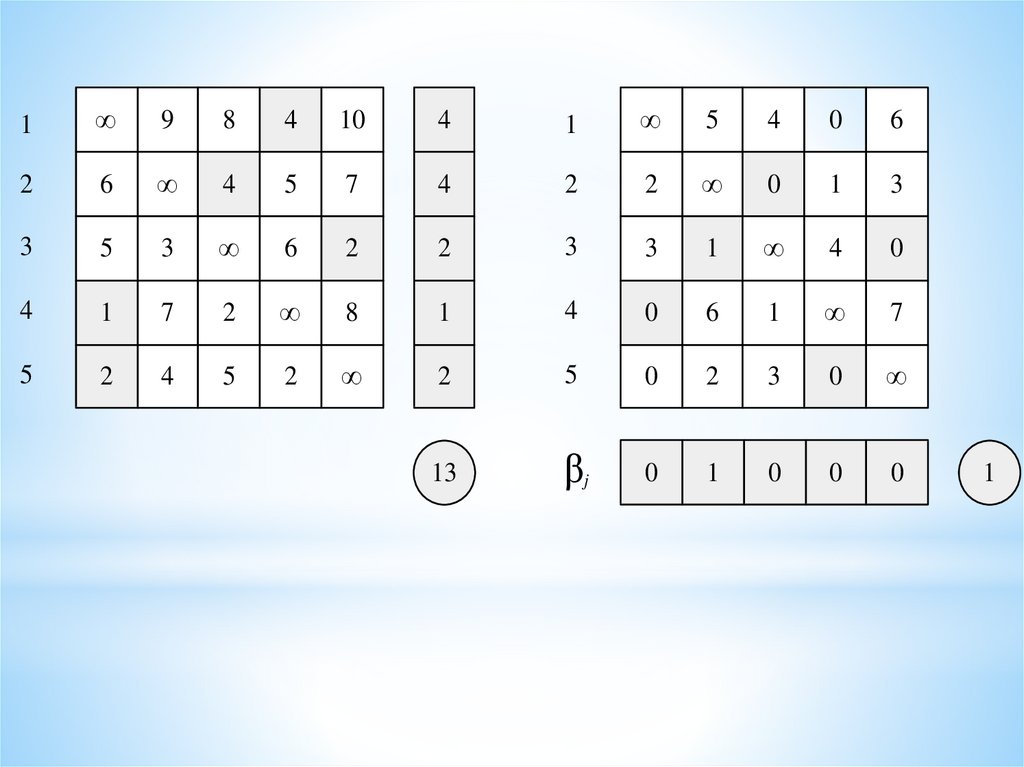
1∞
9
8
4
10
4
1
∞
5
4
0
6
2
6
∞
4
5
7
4
2
2
∞
0
1
3
3
5
3
∞
6
2
2
3
3
1
∞
4
0
4
1
7
2
∞
8
1
4
0
6
1
∞
7
5
2
4
5
2
∞
2
5
0
2
3
0
∞
13
βj
0
1
0
0
0
1
6.
Утверждение 3. Приведение матрицы расстояний не влияет на выбороптимального маршрута коммивояжера.
i j 13 1 14 -
R
сумма констант приведения
i
j
- множество всех допустимых решений (маршрутов);
Утверждение 4.
( R) ( R) - нижняя граница длины маршрута
Если бы после приведения матрицы расстояний все ее элементы были бы
равны 0, то длина кратчайшего маршрута была бы равна .
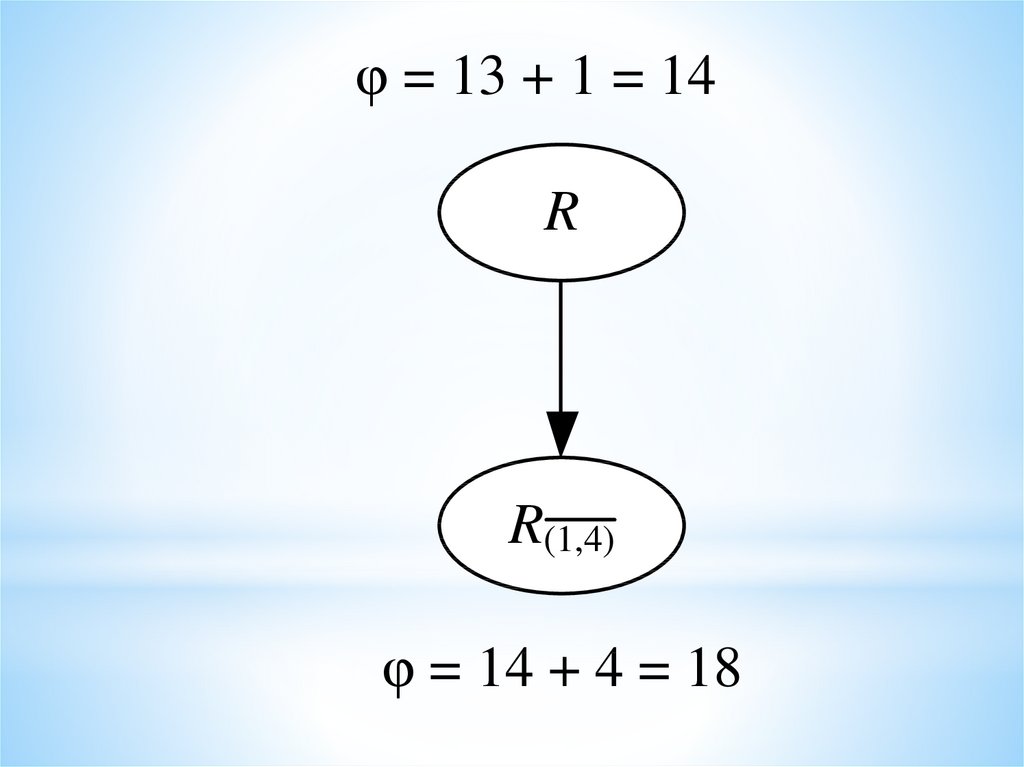
φ = 13+1 = 14
R
7.
12
∞
1
2
4
3
4
5
0
1
1
1
3
3
4
∞
5
1
∞
4
4
∞
6
2
2
∞
0
1
3
3
3
0
∞
4
0
4
0
5
1
∞
7
5
0
1
3
0
2
3
4
5
1
∞
4
4
0
6
3
2
2
∞
0
1
3
4
0
3
3
∞
∞
4
0
1
∞
7
4
0
5
1
∞
7
3
0
∞
5
0
1
3
0
∞
2
3
4
5
1
∞
4
4
0
6
2
2
∞
∞
1
3
3
0
∞
4
0
5
5
0
1
2
7
0
4
1
1
0
∞
3
2
6
1
∞
5
5
0
0
0
0
4
4
∞
2
3
3
1
1
2
3
4
5
1
∞
4
4
0
6
1
∞
4
4
0
6
2
2
∞
0
1
3
2
2
∞
0
1
3
3
3
0
∞
4
∞
3
3
0
∞
4
0
4
0
5
1
∞
7
4
∞
5
1
∞
7
5
0
1
3
0
∞
5
0
1
3
0
∞
1
3
∞
4
1
2
3
4
5
1
∞
4
4
0
6
1
∞
4
4
0
6
2
2
∞
0
1
3
2
2
∞
0
1
3
3
3
0
∞
4
0
3
3
0
∞
4
0
4
0
5
1
∞
7
4
0
5
1
∞
7
5
∞
1
3
0
∞
5
0
1
3
∞
∞
0
0
8.
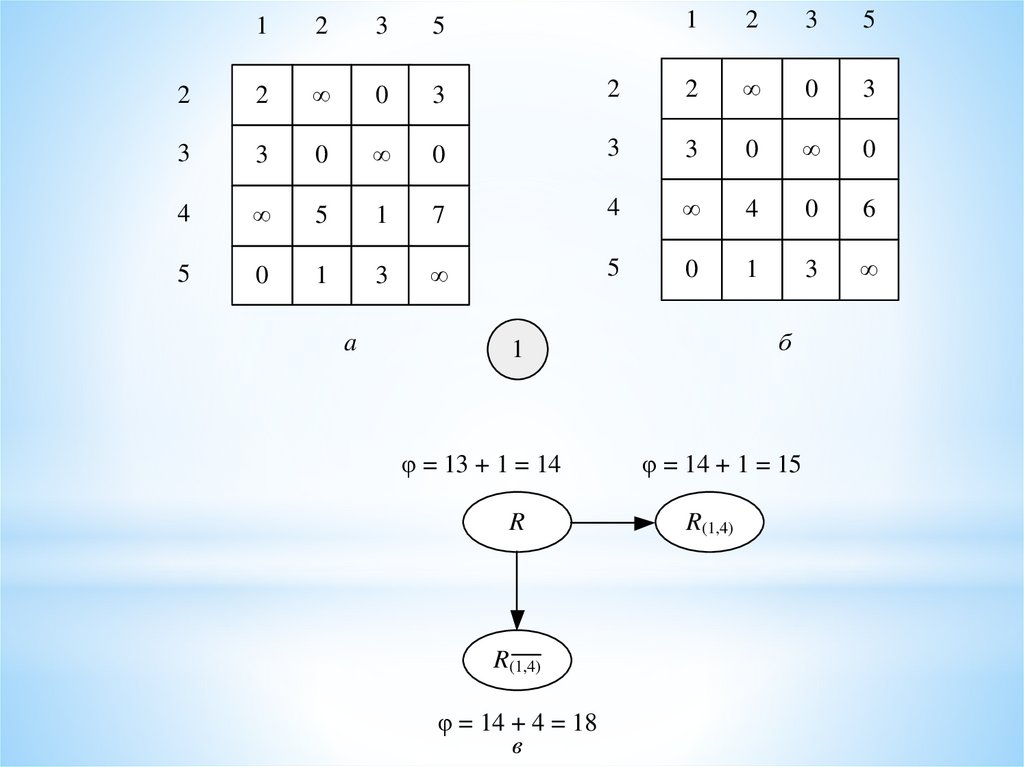
φ = 13 + 1 = 14R
R(1,4)
φ = 14 + 4 = 18
9.
12
3
5
2
2
∞
0
3
0
3
3
0
∞
0
1
7
4
∞
4
0
6
3
∞
5
0
1
3
∞
1
2
3
5
2
2
∞
0
3
3
3
0
∞
4
∞
5
5
0
1
a
б
1
φ = 13 + 1 = 14
R
R(1,4)
φ = 14 + 4 = 18
в
φ = 14 + 1 = 15
R(1,4)
10.
12
3
5
1
2
3
5
2
2
∞
0
3
2
2
∞
0
3
3
3
0
∞
0
3
3
0
∞
0
4
∞
4
∞
6
4
∞
0
∞
2
5
0
1
3
∞
5
0
1
3
∞
1
2
5
4
1
2
5
2
2
∞
3
2
0
∞
1
3
3
0
0
3
3
0
0
5
0
1
∞
5
0
1
∞
2
11.
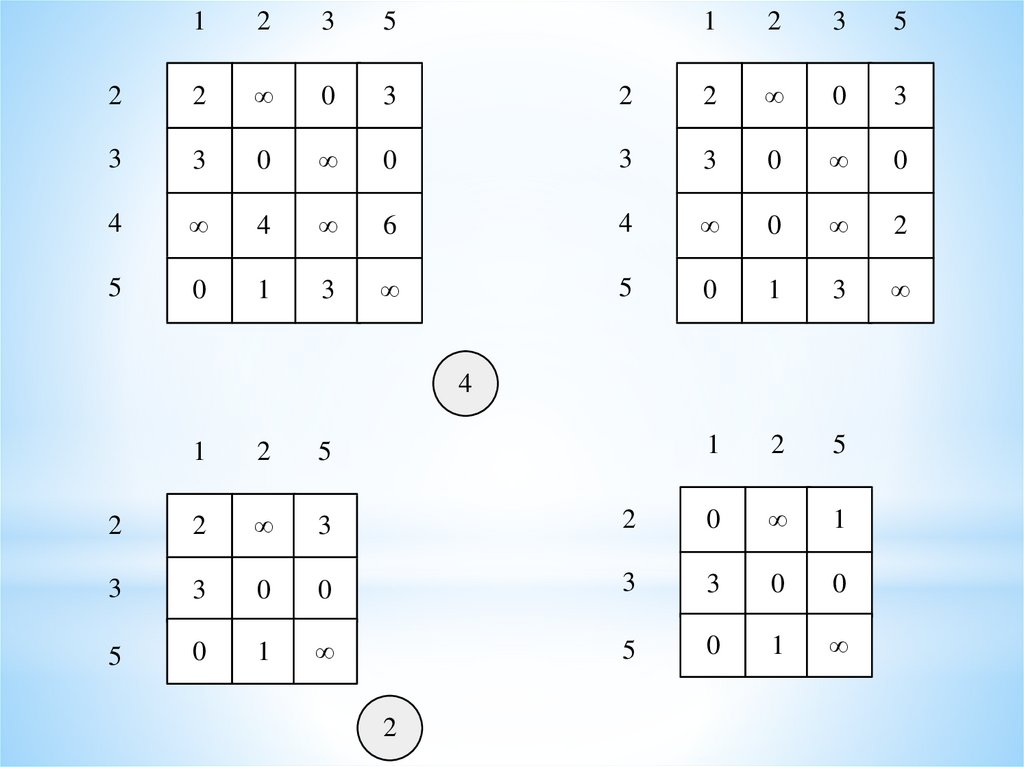
φ = 13 + 1 = 14R
R(1,4)
φ = 14 + 4 = 18
φ = 14 + 1 = 15
R(1,4)
R(1,4)(4,3)
φ = 15 + 4 = 19
φ = 15 + 2=17
R(1,4)(4,3)
12.
12
5
2
∞
∞
0
0
3
3
0
0
∞
5
0
1
∞
1
2
5
2
∞
∞
1
3
3
0
5
0
1
a
φ = 13 + 1 = 14
R
R(1,4)
φ = 14 + 4 = 18
2
5
3
∞
0
5
1
∞
в
2
5
3
∞
0
5
0
∞
1
б
1
φ = 14 + 1 = 15
φ = 15 + 2=17
R(1,4)
R(1,4)(4,3)
R(1,4)(4,3)(2,1)
R(1,4)(4,3)
φ = 15 + 4 = 19
д
φ = 17 + 1=18
φ = 17 + 1=18
R(1,4)(4,3)(2,1)
г
13.
φ = 18 +0=18φ = 14 + 1 = 15
R
R(1,4)
φ = 14 + 4 = 18
R(1,4)
R(1,4)(4,3)
φ = 15 + 4 = 19
φ = 15 + 2=17
R(1,4)(4,3)
R(1,4)(4,3)(2,1)
φ = 17 + 1=18
φ = 17 + 1=18
R(1,4)(4,3)(2,1)
(3, 5)
(5, 2)







 Математика
Математика








