Похожие презентации:
Теория множеств. Cоответствия. Функции. Отображения. Лекция 2
1. ТЕОРИЯ МНОЖЕСТВ CООТВЕТСТВИЯ. ФУНКЦИИ. ОТОБРАЖЕНИЯ
ДИСКРЕТНАЯ МАТЕМАТИКАТЕОРИЯ МНОЖЕСТВ
CООТВЕТСТВИЯ. ФУНКЦИИ.
ОТОБРАЖЕНИЯ
ЛЕКЦИЯ 2
Факультет компьютерной инженерии и управления,
кафедра АПВТ, ХНУРЭ
Харьковский национальный университет радиоэлектроники,
кафедра АПВТ, тел. 7021 326, е-mail: ri@kture.kharkov.ua
1
2. Цель лекции – ознакомиться и овладеть понятием «соответствие», изучить свойства соответствий для применения в задачах компьютерной инже
Соответствия. Функции. ОтображенияCентябрь, 2006
Тема: Соответствия. Функции. Отображения
Цель лекции – ознакомиться и овладеть понятием
«соответствие», изучить свойства соответствий для
применения в задачах компьютерной инженерии
Содержание:
• Понятие упорядоченной пары и вектора
• Декартово произведение множеств
• Определение соответствия
• Свойства соответствий
• Взаимно-однозначное соответствие
• Функции
• Отображения
• Примеры применения в теории кодирования
и задачах диагностирования
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
2
3.
Соответствия. Функции. ОтображенияCентябрь, 2006
Литература
• Горбатов В.А. Основы дискретной математики. М.: Высш. шк., 1986. С.
9-12.
• Тевяшев А.Д., Гусарова И.Г. Основы дискретной математики в
примерах и задачах. Харьков: ХТУРЭ, 2001. С. 11-17.
• Лавров И.А., Максимова Л.Л. Задачи по теории множеств,
математической логике и теории алгоритмов. М.: Наука. Главная
редакция физико-математической литературы, 1984. 4-10 с.
• Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для
инженера. М.: Энергия, 1980. 344 с.
• Новиков Ф.А. Дискретная математика для программистов. С.-П., 2001.
С. 4-24.
• Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні
вказівки до практичних занять з курсу “Дискретна математика”. Харків,
ХНУРЕ. 2001. 87с.
• Хаханов В.И., Чумаченко С.В. Дискретная математика. Электронный
учебник. ХНУРЭ: Электронная библиотека кафедры АПВТ (ауд. 320)
NSERV\Library\Чумаченко\Дискретная математика\...
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
3
4.
Соответствия. Функции. ОтображенияCентябрь, 2006
Термины
Базовые понятия:
множество
упорядоченная
пара
подмножество
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
Ключевые слова:
декартово (прямое)
произведение
множеств
соответствие
всюду
определенность
сюръективность
инъективность
функциональность
биекция (взаимная
однозначность)
4
5.
Соответствия. Функции. ОтображенияCентябрь, 2006
Основные понятия: упорядоченная пара, вектор
Множество
Упорядоченная
пара
Информация
Упорядоченная пара является одним из первичных
понятий в теории множеств
Под упорядоченной парой следует понимать
двухэлементное упорядоченное множество
Вектор (кортеж) представляет собой упорядоченный набор
элементов
х = (х1, х2, …, хn), где хi – координаты (компоненты)
Длина (размерность) вектора определяется количеством
его координат
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
5
6.
Соответствия. Функции. ОтображенияCентябрь, 2006
Проекция вектора на ось
Два вектора x, y одинаковой размерности равны, если
их соответствующие компоненты равны:
x=y i xi=yi
Def: проекцией вектора х=(х1, х2, …, хn) на i-ю ось
называется его i-й компонент Pr i x = хi
Def: пусть V – множество векторов одинаковой длины,
тогда проекцией множества V на i-ю ось называется
множество проекций всех векторов из V:
Pri V Pri v | v V
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
6
7.
Соответствия. Функции. ОтображенияCентябрь, 2006
Примеры
Координаты точки плоскости
образуют упорядоченную пару:
на первой позиции – абсцисса, на
второй – ордината. Они являются
проекциями на первую и вторую
оси соответственно
Дано множество V векторов
размерности 3:
V = { (a,b,c), (c,b,d), (b,b,d) }
Найти проекции множества V на
оси
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
y
y1
0
(x1, y1)
x1
x
Pr1V={a,c,b}
Pr2V={b}
Pr3V={c,d}
7
8.
Соответствия. Функции. ОтображенияCентябрь, 2006
Декартово (прямое) произведение множеств
1
Def: прямое (декартово) произведение множеств
A и B есть множество всех упорядоченных пар (a,b)
таких, что a A, b B:
A B={ (a,b) | a A, b B }
Примеры
1. Декартово произведение множеств А={1,2}, B={3,4,5}
есть
А B = { (1,3), (1,4), (1,5), (2,3), (2,4), (2,5) }
2. A={1,2,3,4,5,6,7,8}, B={a,b,c,d,e,f,g,h}
А В – обозначение клеток шахматной доски
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
8
9.
Соответствия. Функции. ОтображенияCентябрь, 2006
Декартово (прямое) произведение множеств
Декарту принадлежит координатное
представление точек плоскости
2
Множество точек плоскости R R=R есть
множество пар вида (a,b), a R, b R :
R2={(a,b) | a R, b R}
Декартов квадрат (А=В):
А А=А2={(a,b) | a А, b А}
2
Рене Декарт
XVI-XVII вв.
Def: прямое произведение n множеств
А1 А2 ¾ Аn ={(а1, а2, …… , аn)| ai Аi , i=1,n}
Мощность декартова произведения
множеств:
| А1 А2 … Аn | = |А1 |•|А2|• ¾ •|Аn|
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
9
10.
Соответствия. Функции. ОтображенияCентябрь, 2006
Соответствия
Def: соответствие – подмножество декартова
произведения двух множеств:
G A B
А – область определения (множество отправления)
соответствия G :
Pr1G={ x | (x,y) G }
В – область значений (множество прибытия)
соответствия G :
Pr2G={ y | (x,y) G }
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
10
11.
Соответствия. Функции. ОтображенияCентябрь, 2006
Образы и прообразы
Def: множество всех элементов y B, соответствующих
элементу x A, называется образом элемента х
в множестве B при соответствии G.
Def: множество всех элементов x A, которым
соответствует элемент y B, называется прообразом
элемента y в множестве A при соответствии G.
Пример
А={1,2,3}, B={e,f,g}
G={(1,e), (2,e)} A B
A
B
1.
2.
3.
.e
.f
.g
G
прообразы образы
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
11
12.
Соответствия. Функции. ОтображенияCентябрь, 2006
Time Out
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
12
13.
Соответствия. Функции. ОтображенияCентябрь, 2006
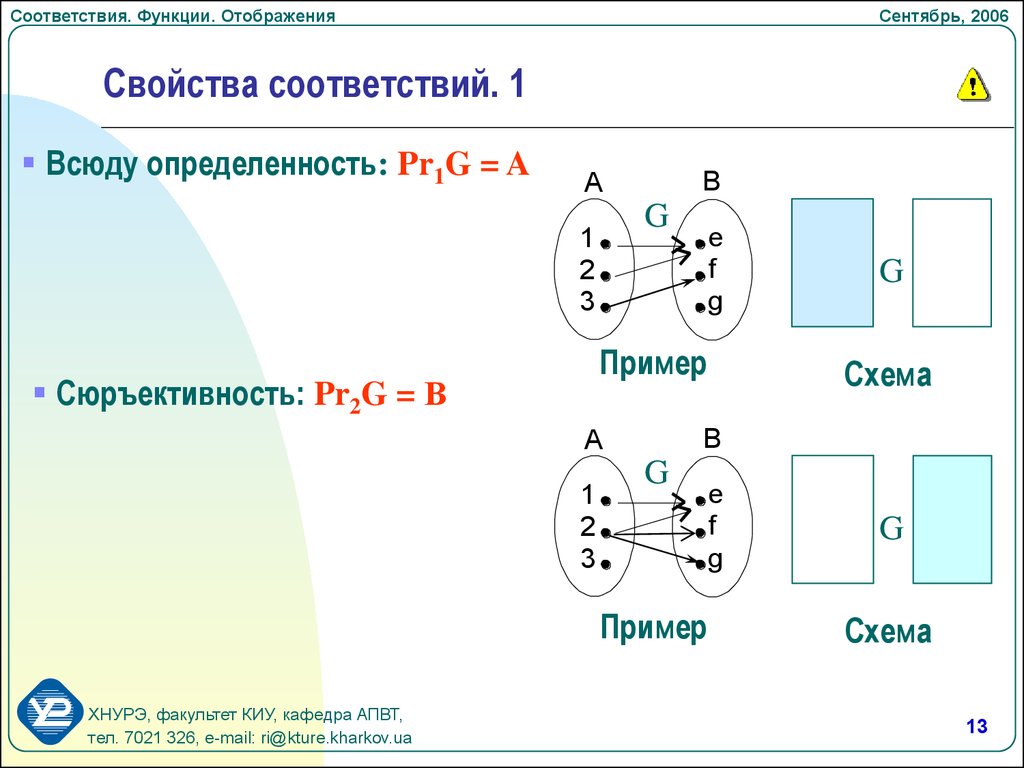
Свойства соответствий. 1
Всюду определенность: Pr1G = A
1.
2.
3.
Сюръективность: Pr2G = В
B
A
G
.e
.f
.g
Пример
G
.e
.f
.g
Пример
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
Схема
B
A
1.
2.
3.
G
G
Схема
13
14.
Соответствия. Функции. ОтображенияCентябрь, 2006
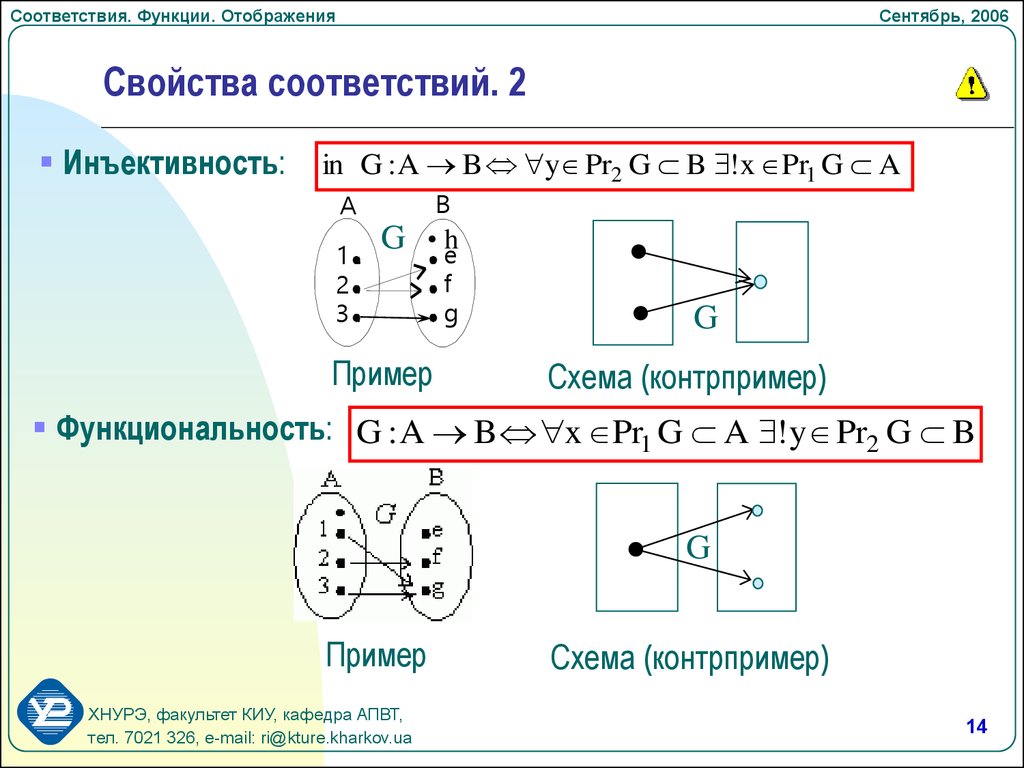
Свойства соответствий. 2
Инъективность:
in G : A B y Pr2 G B !x Pr1 G A
B
A
1.
2.
3.
G •. eh
.f
.g
Пример
G
Схема (контрпример)
Функциональность: G : A B x Pr1 G A ! y Pr2 G B
G
Пример
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
Схема (контрпример)
14
15.
Соответствия. Функции. ОтображенияCентябрь, 2006
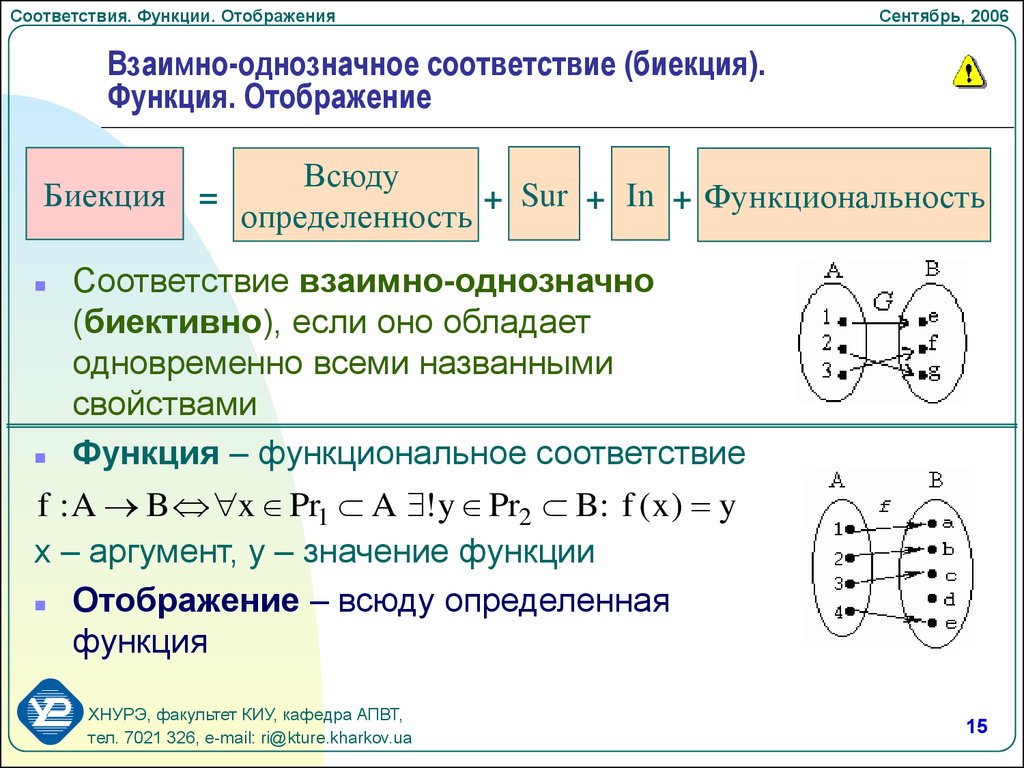
Взаимно-однозначное соответствие (биекция).
Функция. Отображение
Всюду
Биекция =
+ Sur + In + Функциональность
определенность
Соответствие взаимно-однозначно
(биективно), если оно обладает
одновременно всеми названными
свойствами
Функция – функциональное соответствие
f : A B x Pr1 A ! y Pr2 B: f ( x ) y
x – аргумент, y – значение функции
Отображение – всюду определенная
функция
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
15
16.
Соответствия. Функции. ОтображенияCентябрь, 2006
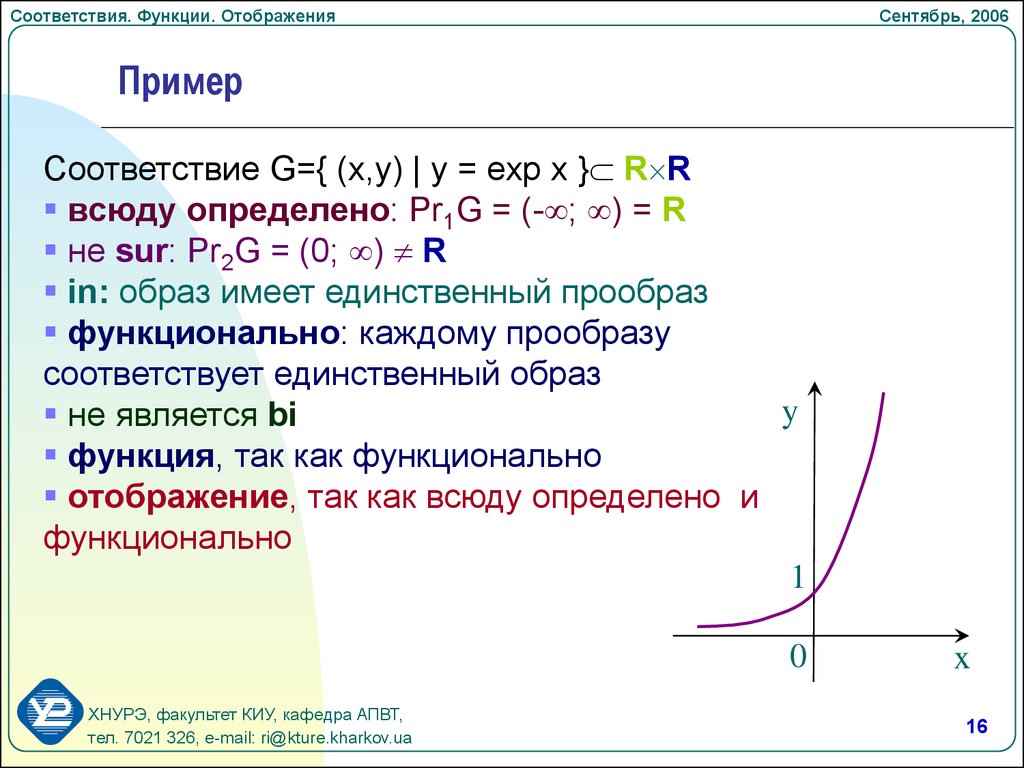
Пример
Соответствие G={ (x,y) | y = exp x } R R
всюду определено: Pr1G = (- ; ) = R
не sur: Pr2G = (0; ) R
in: образ имеет единственный прообраз
функционально: каждому прообразу
соответствует единственный образ
y
не является bi
функция, так как функционально
отображение, так как всюду определено и
функционально
1
0
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
x
16
17. Применение в задачах теории кодирования
Соответствия. Функции. ОтображенияCентябрь, 2006
Применение в задачах теории кодирования
Виды кодирования:
кодирование букв азбукой
Морзе
представление чисел в
системах счисления
секретные шифры
входящие и исходящие
номера в деловой переписке
являются соответствиями
между кодируемыми
объектами и
присваиваемыми им кодами
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
Они обладают всеми
свойствами взаимнооднозначного соответствия,
кроме сюръективности
Единственность образа и
прообраза в кодировании
гарантирует однозначность
шифровки и дешифровки
Отсутствие сюръективности
означает, что не каждый код
имеет смысл. Например,
кодирование телефонов
шестизначными номерами не
сюръективно
17
18. Применение в задачах диагностирования
Соответствия. Функции. ОтображенияCентябрь, 2006
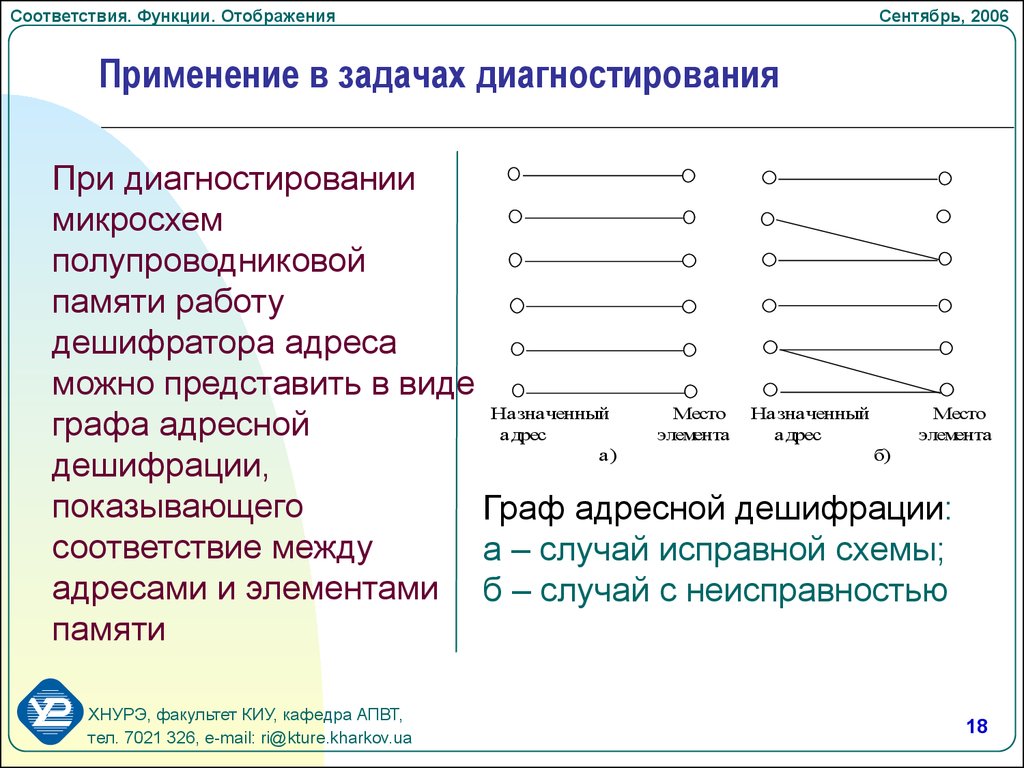
Применение в задачах диагностирования
При диагностировании
микросхем
полупроводниковой
памяти работу
дешифратора адреса
можно представить в виде
Назначенный
Место Назначенный
Место
графа адресной
адрес
элемента
адрес
элемента
а)
б)
дешифрации,
показывающего
Граф адресной дешифрации:
соответствие между
а – случай исправной схемы;
адресами и элементами б – случай с неисправностью
памяти
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
18
19. Выводы
Соответствия. Функции. ОтображенияCентябрь, 2006
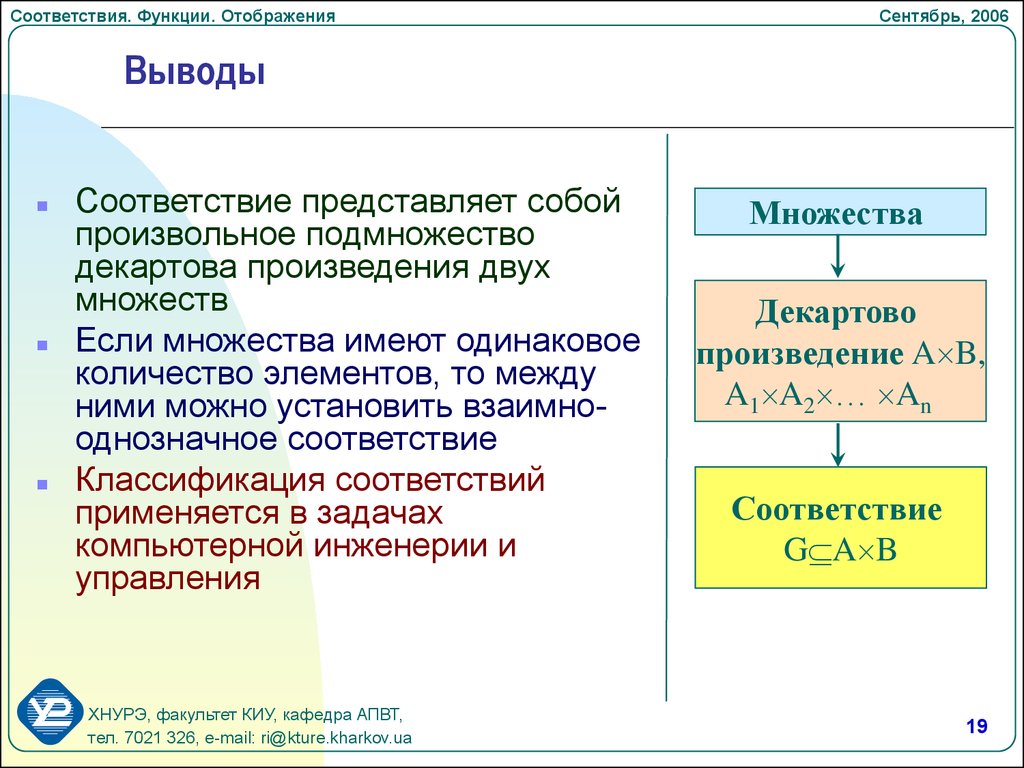
Выводы
Соответствие представляет собой
произвольное подмножество
декартова произведения двух
множеств
Если множества имеют одинаковое
количество элементов, то между
ними можно установить взаимнооднозначное соответствие
Классификация соответствий
применяется в задачах
компьютерной инженерии и
управления
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
Множества
Декартово
произведение A B,
A1 A2 … An
Соответствие
G A B
19
20.
Соответствия. Функции. ОтображенияCентябрь, 2006
Тест-вопросы. 1
1. Могут ли повторяться
компоненты вектора?
а) да; б) нет.
2. Длина вектора
определяется:
а) числом различных
элементов;
б) числом координат.
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
3. Какое из
cоответствий
называется взаимнооднозначным:
а) сюръективное,
инъективное и
функциональное?
б) сюръективное и
инъективное?
в) всюду определенное,
сюръективное,
инъективное и
функциональное?
20
21.
Соответствия. Функции. ОтображенияCентябрь, 2006
Тест-вопросы. 2
4. Является ли
отображение
биективным, если
оно сюръективно и
инъективно?
а) да; б) нет.
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
5. Отображение А в В это:
а) частично определенная
функция;
б) всюду определенная
функция;
в) сюръективное
соответствие;
г) инъективное соответствие.
21
22.
Соответствия. Функции. ОтображенияCентябрь, 2006
Тест-вопросы. 3
8. Верно ли: |Аn| = |A|n ?
6. Верно ли: A,B A B=B A ?
а) да
а) да;
б) нет.
б) нет.
9. Соответствие является
7. Указать проекцию
подмножеством
множества A={(3,3,5), (3,3,6), а) объединения двух
(3,5,5), (3,5,6), (8,3,5), (8,3,6), множеств;
б) пересечения двух
(8,5,5), (8,5,6)}
множеств;
на третью ось
в) теоретико-множественной
а) PrA={3,8},
разности двух множеств;
б) PrA={3,5},
г) декартова произведения
в) PrA={5,6}.
нескольких множеств;
д) декартова произведения
двух множеств.
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
22
















 Математика
Математика








