Машини Тьюринга. Лекція 4

1. Лекція 4. Машини Тьюринга.

2. Питання

1.
2.
3.
Машини з натуральнозначними
регістрами.
Детермінована однострічкова
машина Тьюринга.
Багатострічкова машина Тьюринга.

3. Машина з натуральнозначними регістрами (МНР)

МНР складається із необмеженої послідовності регістрів,
вмістом яких є натуральні числа.
• Регістри нумеруємо натуральними числами, починаючи з 0,
позначаємо їх R0, R1, ..., Rn, ...
• Вмiст регiстру Rn позначаємо rn .
• Послiдовнiсть (r0, r1,..., rn, ...) вмiстiв регiстрiв МНР
називається конфiгурацiєю МНР.
Скiнченний список команд утворює програму МНР.
Команди програми послідовно нумеруємо натуральними
числами, починаючи з 1. Номер команди в програмі
називаються адресою команди.
МНР-програму містить команди, що позначаються I1, I2,..., Ik.
Довжину МНР-програми P позначимо |P|.

4. Команди МНР бувають 4-х типiв.

Тип 1. Обнуління n-го регістру Z(n): rn : 0.
Тип 2. Збільшення вмісту n-го регістру на 1
S(n): rn : rn+1 – інкремент регістру (n=n+1).
Тип 3. Копіювання вмісту регістру T(m, n):
rn : rm (при цьому rm не змінюється).
Тип 4. Умовний перехід J(m, n, q): якщо rn = rm.
Число q в команді J(m, n, q) називається
адресою переходу.

5.

Виконання однієї команди МНР назвемо кроком
МНР.
Результат виконання МНР програми зчитується
з регістра R0 !!!
Обчислення МНР програми завершується,
коли:
1. виконана остання арифметична команда
програми;
2. при виконанні J(m, n, q) виявилось, що rn r m,
але q більше за число команд в програмі;
3. при виконанні J(m, n, q) виявилось, що rn≠r m,
але це була остання команда в програмі.

6.

Якщо МНР-програма P нiколи не зупиняється при
роботi над початковою конфiгурацiєю (a0, a1, ...), це
позначаємо P(a0, a1, ...) , якщо коли-небудь
зупиниться, це позначаємо P(a0, a1,...) .
Якщо МНР-програма P при роботi над початковою
конфiгурацiєю (a0, a1, ...) зупиняється iз фiнальною
конфiгурацiєю (b0, b1, ...), це позначаємо:
P(a0, a1, ...) (b0, b1, ...)
МНР-програма P стандартна, якщо в P для кожної
команди вигляду J(m, n, q) виконується умова
q |P| + 1.

7.

Конкатенацією стандартних МНР-програм P=І1I2...Ik та
Q=I1I2...Im
назвемо
стандартну
МНР-програму
I1...IkIk+1...Ik+m, де команди Ik+1,..., Ik+m є командами
програми Q, у яких кожна команда вигляду J(m, n, q)
замінена командою J(m, n, q + k).
МНР-програми P та Q еквiвалентнi, якщо при роботi
над однаковими початковими конфiгурацiями вони або
обидві зупиняються з однаковими фiнальними
конфiгурацiями, або обидвi не зупиняються.
МНР-програма P обчислює часткову n-арну функцiю
f : Nn→N, якщо
f(a1, a2, ..., aп) = b P(a1, a2, ..., aп) (b, ...).
Функцiя f : Nп→N МНР-обчислювана, якщо iснує МНРпрограма, що обчислює цю функцiю.

8. Основні форми запису МНР-команд

Збільшення вмісту 3-го регістру.
S(3) r3:=r3+1
Обнулення 3-го регістру.
Z(3) r3:=0
Копіювання вмісту першого регістру в
третій.
T(1,3) r3:=r1

9. Приклад 1.

1.
2.
3.
4.
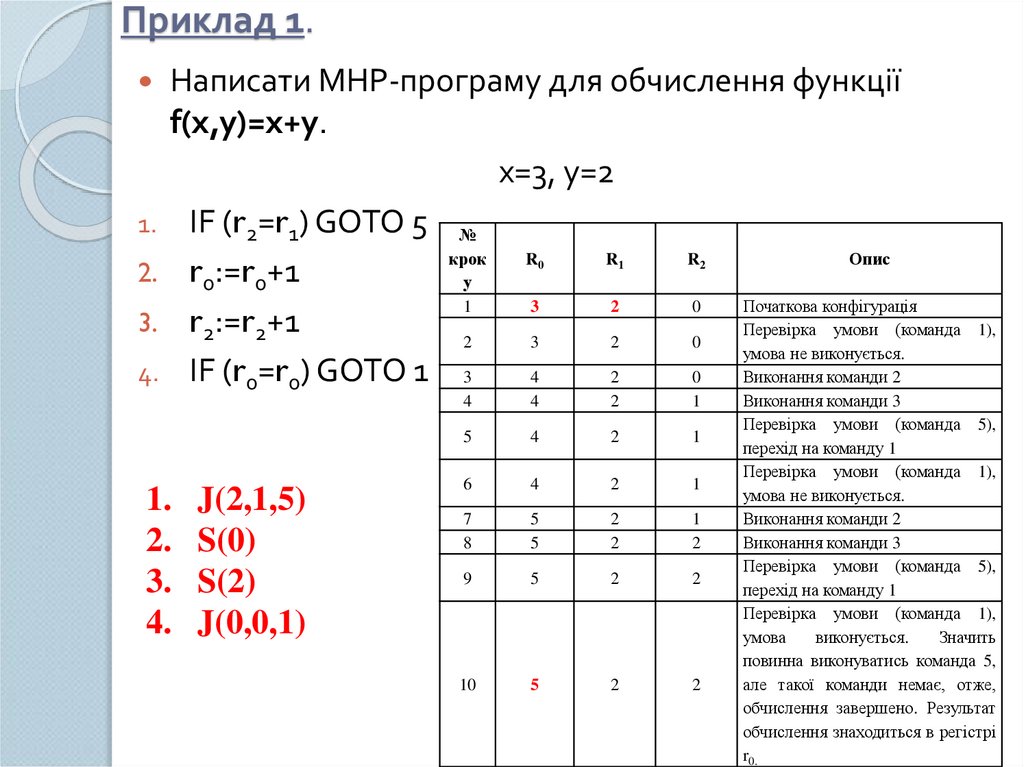
Написати МНР-програму для обчислення функції
f(x,y)=x+y.
x=3, y=2
IF (r2=r1) GOTO 5 №
крок
R
R
R
Опис
r0:=r0+1
у
1
3
2
0
Початкова конфігурація
r2:=r2+1
Перевірка умови (команда
2
3
2
0
умова не виконується.
IF (r0=r0) GOTO 1 3
4
2
0
Виконання команди 2
1.
2.
3.
4.
0
J(2,1,5)
S(0)
S(2)
J(0,0,1)
1
2
4
4
2
1
5
4
2
1
6
4
2
1
7
8
5
5
2
2
1
2
9
5
2
2
10
5
2
2
1),
Виконання команди 3
Перевірка умови (команда 5),
перехід на команду 1
Перевірка умови (команда 1),
умова не виконується.
Виконання команди 2
Виконання команди 3
Перевірка умови (команда 5),
перехід на команду 1
Перевірка умови (команда 1),
умова
виконується.
Значить
повинна виконуватись команда 5,
але такої команди немає, отже,
обчислення завершено. Результат
обчислення знаходиться в регістрі
r0.

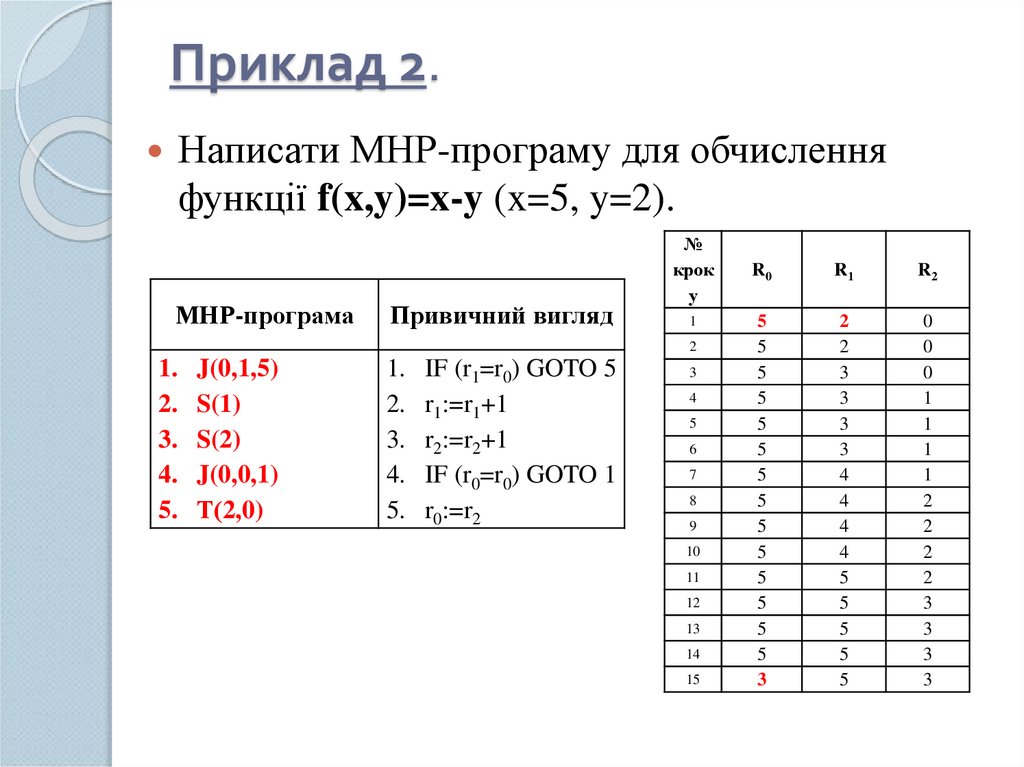
10. Приклад 2.

Написати МНР-програму для обчислення
функції f(x,y)=x-y (x=5, y=2).
МНР-програма
Привичний вигляд
№
крок
у
1
2
1.
2.
3.
4.
5.
J(0,1,5)
S(1)
S(2)
J(0,0,1)
Т(2,0)
1.
2.
3.
4.
5.
IF (r1=r0) GOTO 5
r1:=r1+1
r2:=r2+1
IF (r0=r0) GOTO 1
r0:=r2
3
4
5
6
7
8
9
10
11
12
13
14
15
R0
R1
R2
5
5
5
5
5
5
5
5
5
5
5
5
5
5
3
2
2
3
3
3
3
4
4
4
4
5
5
5
5
5
0
0
0
1
1
1
1
2
2
2
2
3
3
3
3

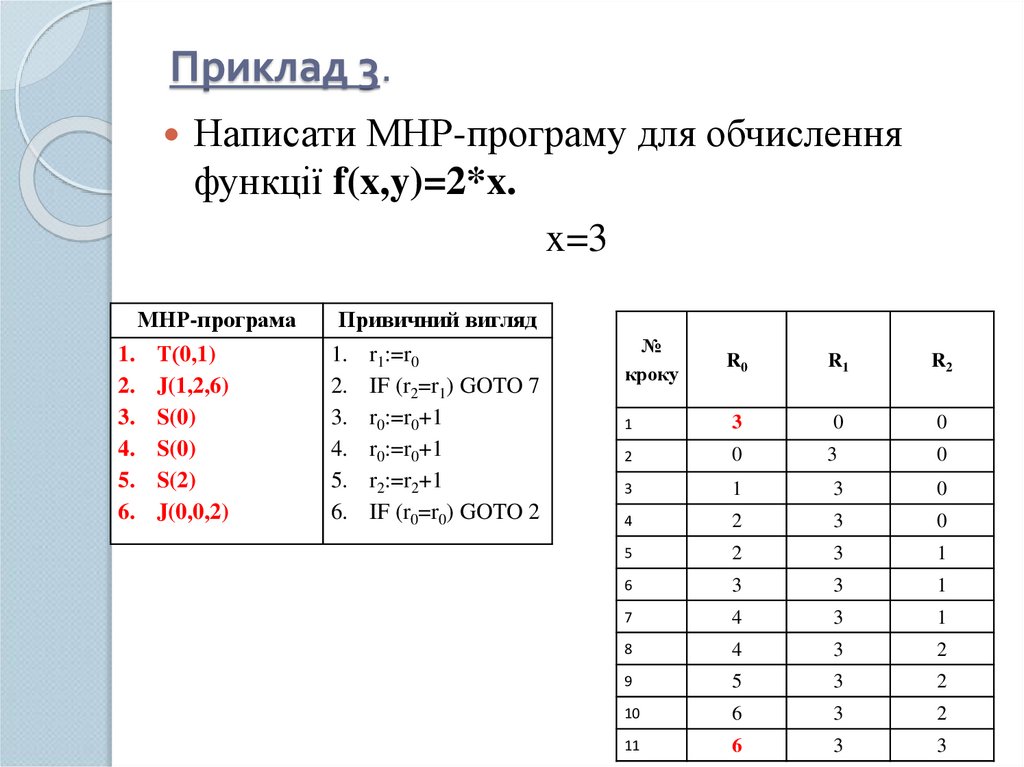
11. Приклад 3.

Написати МНР-програму для обчислення
функції f(x,y)=2*x.
x=3
МНР-програма
1.
2.
3.
4.
5.
6.
Т(0,1)
J(1,2,6)
S(0)
S(0)
S(2)
J(0,0,2)
Привичний вигляд
1.
2.
3.
4.
5.
6.
r1:=r0
IF (r2=r1) GOTO 7
r0:=r0+1
r0:=r0+1
r2:=r2+1
IF (r0=r0) GOTO 2
№
кроку
R0
R1
R2
1
3
0
0
2
0
3
1
3
0
4
2
3
0
5
2
3
1
6
3
3
1
7
4
3
1
8
4
3
2
9
5
3
2
10
6
3
2
11
6
3
3
3
0

12.

Приклад 4. МНР-програма для обчислення
максимального елемента з двох заданих.
f(x, y)=max(x, y):
1. J(0,2,5)
2. J(1,2,6)
3. S(2)
4. J(0,0,1)
5. Т(1,0)
Приклад 5. МНР-програма для функції f(x)=x/2.
1. J(0,2,6)
2. S(2)
3. S(2)
4. S(1)
5. J(0,0,1)
6. Т(1,0)

13.

Машина Тьюринга
Математик
Інформатик
Логік
Криптолог
1936 р.

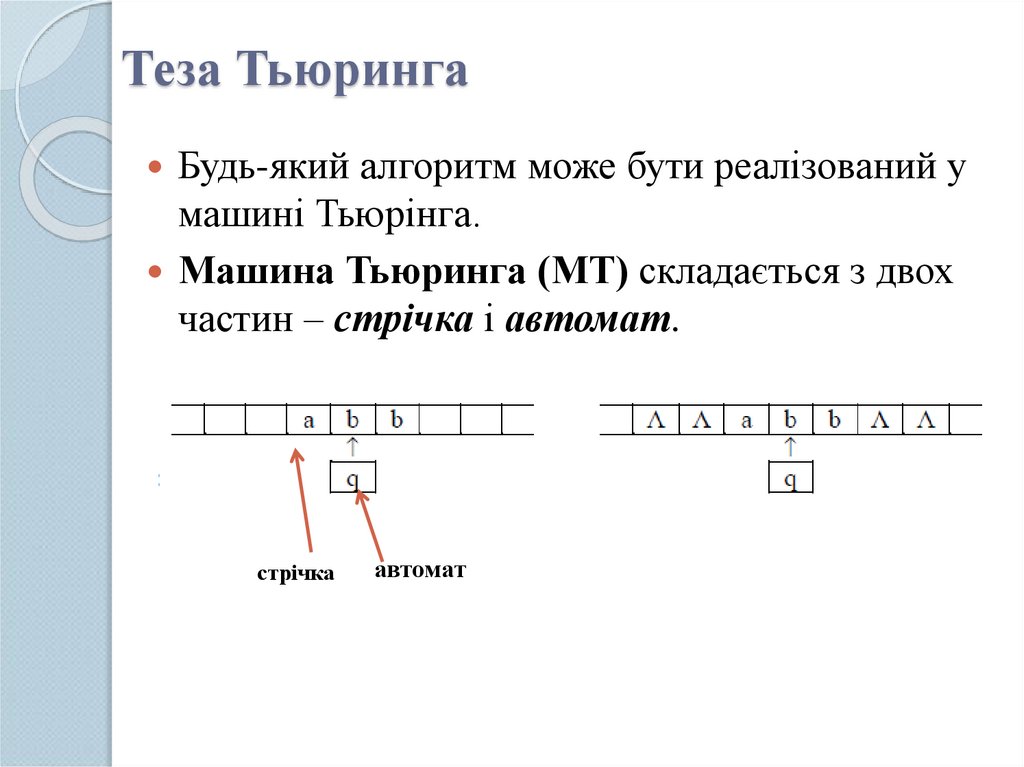
14. Теза Тьюринга

Будь-який алгоритм може бути реалізований у
машині Тьюрінга.
Машина Тьюринга (МТ) складається з двох
частин – стрічка і автомат.
стрічка
автомат

15.

Пару з видимого символу (S) та поточного стану
автомата (q) будемо називати конфігурацією
(S, Q).
Автомат може виконувати три елементарні дії:
1) записувати у видиму комірку новий символ
(змінювати вміст інших комірок автомат не
може);
2) здвигатися на одну комірку вліво або
вправо;
3) переходи в новий стан.

16.

Машиною Тьюринга називають упорядковану шістку
{A, Q, a0, q0, q1, P}, яка задовольняє таким умовам:
1. Множини A і Q скінчені, не перетинаються і не
містять символів →, L, R;
2. a0∈А, q0∈Q, q1∈Q. При цьому a0 називається
символом порожньої комірки, q1 – початковий стан
машини, q0 – стан, у якому машина зупиняється;
3. Р – програма із зовнішнім алфавітом А і внутрішнім
алфавітом Q, причому:
програма не містить двох різних команд з
однаковими лівими частинами;
будь-яка з команд не починається символом q0.

17. Такт роботи машини Тьюринга

Такт роботи машини Тьюринга
На кожному такті МТ виконує три дії:
1. записує деякий символ S у видиму комірку;
2. здвигатися на одну комірку вліво (L), або на одну
комірку вправо (R), або залишається нерухомим
(N).
3. переходить в деякий стан q (зокрема, може
залишатися в попередньому стані).
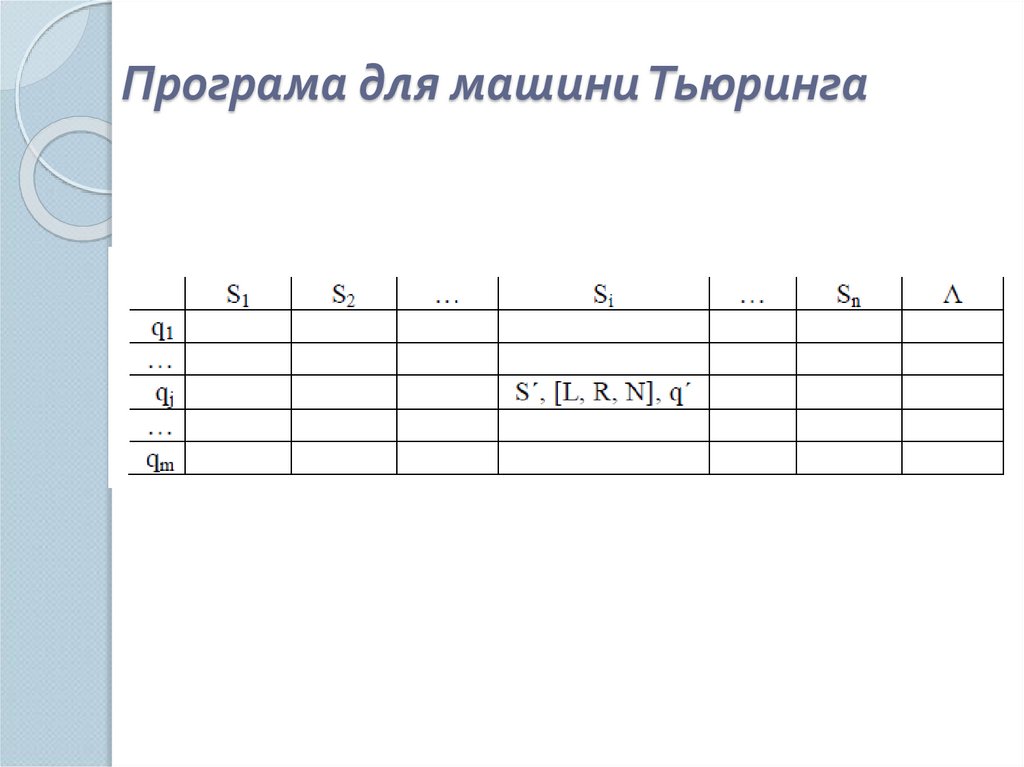
Формально дії одного такту буде записувати в
трійку:
S , [ L, R, N ], q
Запис
такту
командою МТ.
для
конфігурації
називають

18. Програма для машини Тьюринга

19. Правила виконання програми

МТ в початковій конфігурації, що визначена
наступним чином:
1. на стрічку записано вхідне слово (в середині без
пустих комірок, справа та зліва від слова порожні
комірки);
2. автомат встановлений у стані q1 та розміщений
під його першим (самим лівим) символом
вхідного слова;
3. виконання команд програми.

20. Такт зупинки

Такт зупинки - це такт, що нічого не змінює: автомат записує
у видиму комірку той же символ, що і був в ній раніше, не
здвигається і залишається у попередньому стані, тобто це
такт S,N,q для конфігурації (S, q).
Виходи МТ над вхідним словом:
1) Перший вихід – «хороший»: це коли в якийсь момент МТ
зупиняється (попадає на такт зупинки). В такому випадку
говорять, що МТ застосовна до заданого вхідного
слова. Це слово, що до цього моменту отримано на стрічці,
вважається вихідним словом, тобто результатом роботи
МТ.
2) Другий вихід – «поганий»: це коли МТ зациклюється,
ніколи не попадає на такт зупинки (наприклад, автомат на
кожний крок здвигається вправо і тому не може
зупинитися,
тому
що
стрічка
нескінчена).
У
цьому випадку говорять, що МТ не застосовується до
заданого вхідного слова. Ні про якийсь результат при
такому виході не може й бути мови.

21. Угоди для скорочення запису програми МТ

При конфігурації (a , q1)
а, R, q3 = , R, q3 (але ні Λ, R, q3 !!)
b, N, q2 = b, , q2
a, L, q1 = , L,
a, N, q1 = , , (це такт зупинки)
b. такт b, L , ! - запис символу b у видиму комірку
стрічки, здвиг вліво та зупинка
c.
a)

22. Приклади на складання програм МТ

Приклад 6.
Переміщення автомата, заміна символів.
А= {0,1,2,3,4,5,6,7,8,9}.
Нехай Р - непусте слово; значить, Р – це послідовність десяткових цифр,
тобто запис невід’ємного цілого числа в десятковій системі. Потрібно
отримати на стрічці запис числа, яке на 1 більше числа Р.
0
1
2
3
4
5
6
7
8
9
Λ
q1
,R,
,R,
,R,
,R,
,R,
,R,
,R,
,R,
,R,
,R,
,L,q2
q2
1, ,!
2, ,!
3, ,!
4, ,!
5, ,!
6, ,!
7, ,!
8, ,!
9, ,!
0,L,
1, ,!
коментар
під
останню
цифру
видима
цифра+1

23.

Приклад 7.
Аналіз символів.
А={a,b,c}
Перенести перший символ непустого слова Р в його
кінець.
a
b
c
Λ
q1
Λ,R,q2
Λ,R,q3
Λ,R,q4
,R,
аналіз 1-го
розгалуження
q2
q3
q4
,R,
,R,
,R,
,R,
,R,
,R,
,R,
,R,
,R,
a, ,!
b, ,!
c, ,!
запис а справа
запис b справа
запис c справа
коментар
символу, видалення
його,

24.

Приклад 8.
Видалення символу зі слова.
А = {a , b}.
Видалити зі слова Р його другий символ, якщо такий є.
a
b
Λ
коментар
q1
Λ,R,q2
Λ,R,q3
, ,!
аналіз та видалення 1-го символу,
розгалуження
q2
, ,!
а, ,!
a, ,!
заміна 2-го символу на а
q3
b, ,!
, ,!
b, ,!
заміна 2-го символу на запис b

25.

Приклад 9.
Вставка символу в слово
А = {a, b, c}
Якщо Р – не порожнє слово, то за його першим
символом вставити символ a.
a
b
c
Λ
коментар
q1
,L,q2
,L,q3
,L,q4
, ,!
аналіз 1-го символу для переносу його
вліво
q2
a,R,q5
запис а зліва
q3
b,R,q5
запис b зліва
q4
c,R,q5
запис c зліва
q5
, ,!
a, ,!
a, ,!
Замінити попередній 1-й символ на а

26. Детермінована однострічкова машина Тьюринга.

Алфавітом називається довільна не порожня злічена
множина.
Зазвичай розглядають кінцеві алфавіти.
Елементи алфавіту називаються символами або
буквами.
Словом в алфавіті A називається кінцева послідовність
літер з цього алфавіту.
Кількість букв в слові x називається довжиною слова і
позначається |x|.
A* = множина всіх слів над алфавітом A.
Ak = множина всіх слів довжини k.

27. Детермінована однострічкова машина Тьюринга.

Детермінована однострічкова машина Тьюринга (ДМТ)
– це четвірка M = (Q, A,S, Π), де:
A – «стрічковий» алфавіт (містить спеціально виділений
символ ∧ - «пробіл»),
Q = {q0, q1, ..., qm} – алфавіт станів,
S = {- 1, 0, +1} – алфавіт здвигів,
Π – програма, що представляє собою відображення Q × A
→ Q × A × S.
Часова та ємнісна складність МТ:
TМ(x) – кількість кроків, зроблених машиною M при
обробці входу x,
SМ(x) – кількість комірок на стрічці, на яких побував
автомат машини M при обробці входу x.

28.

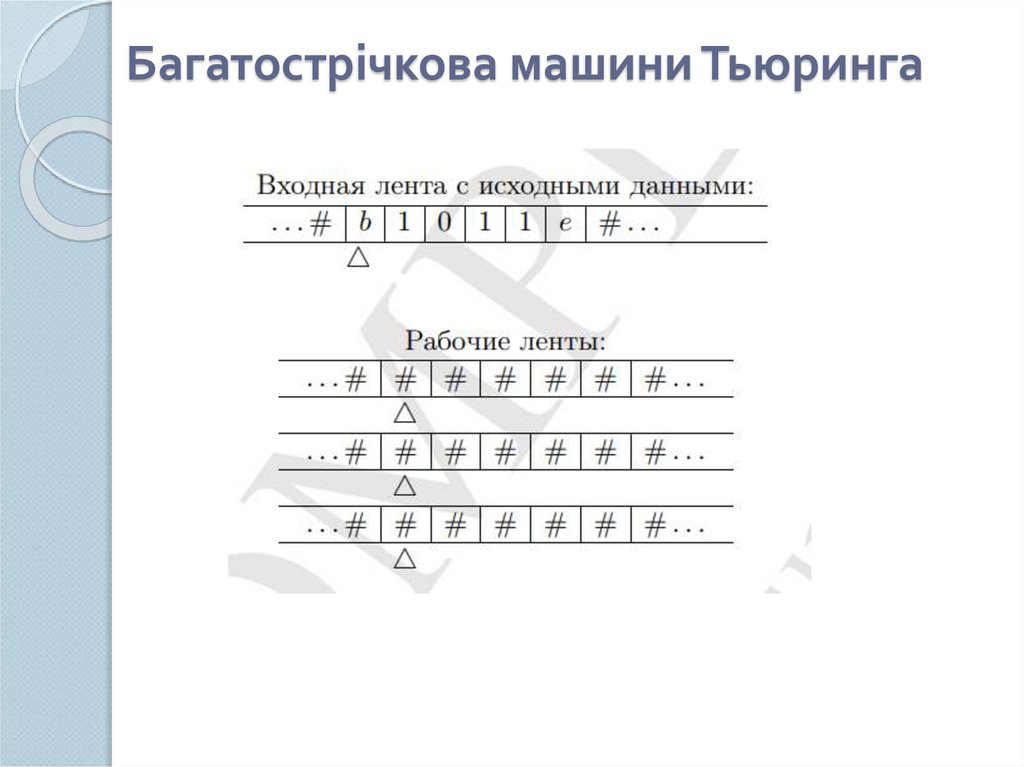
Багатострічкова машини Тьюринга

29. Багатострічкова машини Тьюринга

Нехай k – ціле число, k ≥ 1, k-стрічкова машина
Тьюринга – це п'ятірка M = (k, A, Q,
S, Π), де Π: Q × Ak →Q × (A × S)k.
Черговий крок багатострічкової МТ визначається
символами, розташованими в поточних комірках на
всіх стрічках, тобто набором (q,a1, ..., ak)∈Q × Ak. З
цього
набору
визначаються
дії,
що
виконуються: (q', b1, s1, ..., bk, sk) ∈ Q × (A × S)k.

30. Часова та ємнісна складність багатострічкової машини Тьюринга

Часова
складність
багатострічкової
машини
визначається точно так же, як і для однострічковій.
У визначенні ємнісної складності є невелика зміна:
ємнісна складність k - стрічкової МТ M на
вході x SМ(x) визначається як максимум кількості
комірок, на яких при обробці входу x побували головки
машини M на всіх стрічках.
ТЕОРЕМА. Для будь-якої машини Тьюринга
виконується нерівність S (n) ≤ T (n), тобто ємнісна
складність не перевищує часову.