Імітаційне моделювання

1.

Навчально-науковий інститут комп’ютерних інформаційних технологій
Кафедра комп’ютеризованих систем управління
Навчальна дисципліна
«ІМІТАЦІЙНЕ МОДЕЛЮВАННЯ»
Спеціальність 123 «Комп’ютерна інженерія»
Спеціалізація 123.2 «Системне програмування»
Курс 3
Семестр 6
Аудиторних занять –
48 годин
Самостійна робота –
72 години
Всього (годин/кредитів ECTS) – 120/4,0
Диференційований залік –
6 семестр
Викладач: Литвиненко Олександр Євгенійович –
завідувач кафедри КСУ, доктор техн. наук, професор

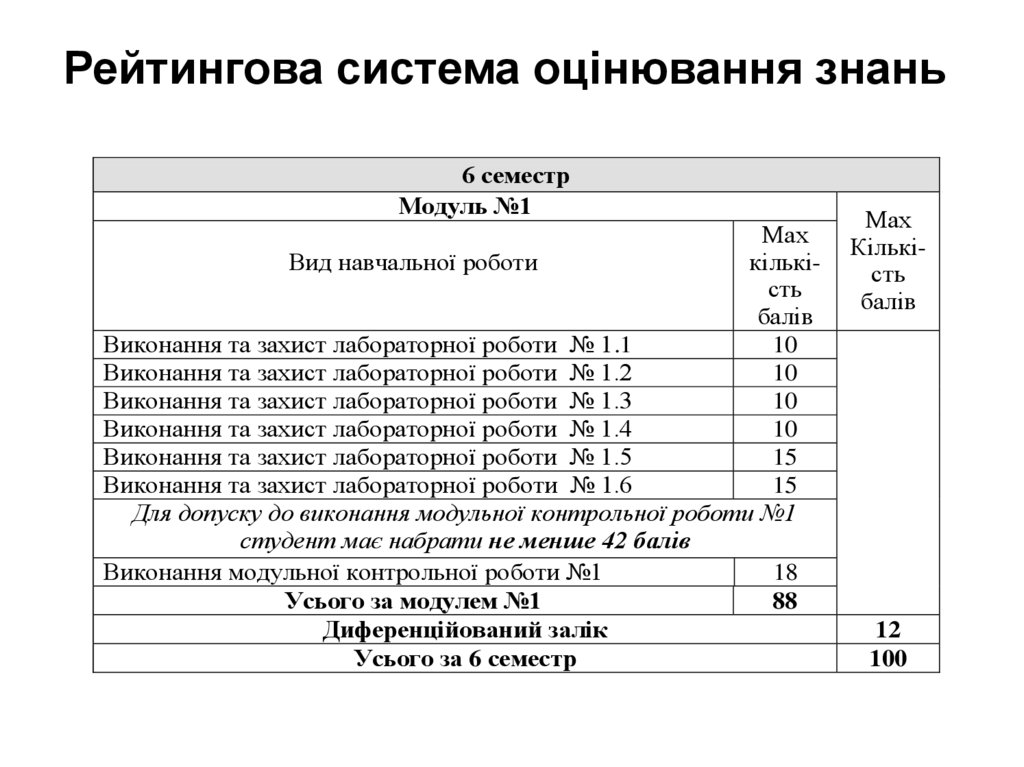
2. Рейтингова система оцінювання знань

6 семестр
Модуль №1
Модуль №2
Вид навчальної роботи
Мах
кількість
балів
Виконання та захист лабораторної роботи № 1.1
10
Виконання та захист лабораторної роботи № 1.2
10
Виконання та захист лабораторної роботи № 1.3
10
Виконання та захист лабораторної роботи № 1.4
10
Виконання та захист лабораторної роботи № 1.5
15
Виконання та захист лабораторної роботи № 1.6
15
Для допуску до виконання модульної контрольної роботи №1
студент має набрати не менше 42 балів
Виконання модульної контрольної роботи №1
18
Усього за модулем №1
88
36
Диференційований
залік
УсьогоУсього
за модулем
№2
за 6 семестр
Мах
Кількість
балів
12
100

3. ЗМІСТ ДИСЦИПЛІНИ

1. Основні поняття теорії моделювання
2. Моделювання випадкових явищ
3. Технологія імітаційного моделювання
4. Обробка результатів імітаційного
моделювання

4.

Мета викладання дисципліни: засвоєння методів імітаційного
моделювання складних систем.
Студент повинен знати:
● методи імітаційного моделювання випадкових явищ;
● принципи побудови моделюючих алгоритмів;
● методи обробки та інтерпретації результатів імітаційних
експериментів.
Студент повинен вміти:
● формалізувати процес функціонування складних систем;
● обчислювати кількісні характеристики випадкових явищ;
● обробляти результати імітаційних експериментів;
● розраховувати необхідну кількість реалізацій моделюючого
алгоритму.

5.

ЛІТЕРАТУРА
1. Акопов А.С. Имитационное моделирование : учебник и практикум для
академического бакалавриата / М. : Издательство Юрайт, 2014. — 389 с.
2. Кельтон Д., Аверил М. Имитационное моделирование. — СПб.: Питер,
2004. — 848 с.
3. Кельтон В., Лоу А., Имитационное моделирование. Классика CS. 3-е
изд. – СПб.: Питер; – Киев: Издательская группа BHV, 2004. — 847 с.
4. Белотелов Н.В Имитационное моделирование / Н.В. Белотелов,
Ю.И. Бродский. – Москва: Издательский центр «Академия», 2008. — 236 с.
5. Рыжиков Ю.И. Имитационное моделирование. Теория и технологии. –
М.: Альтекс, 2004. — 529 с.
6. Харин Ю.С., Малюгин В.И., Кирлица В.П. Основы имитационного и
статистического моделирования: Учеб. пособие. — Минск: Дизайн ПРО,
1997. — 288 с.
7. Карпов Ю. Имитационное моделирование систем. Введение в
моделирование. – СПб.: Питер, Издательская группа BHV, 2004. — 400 с.

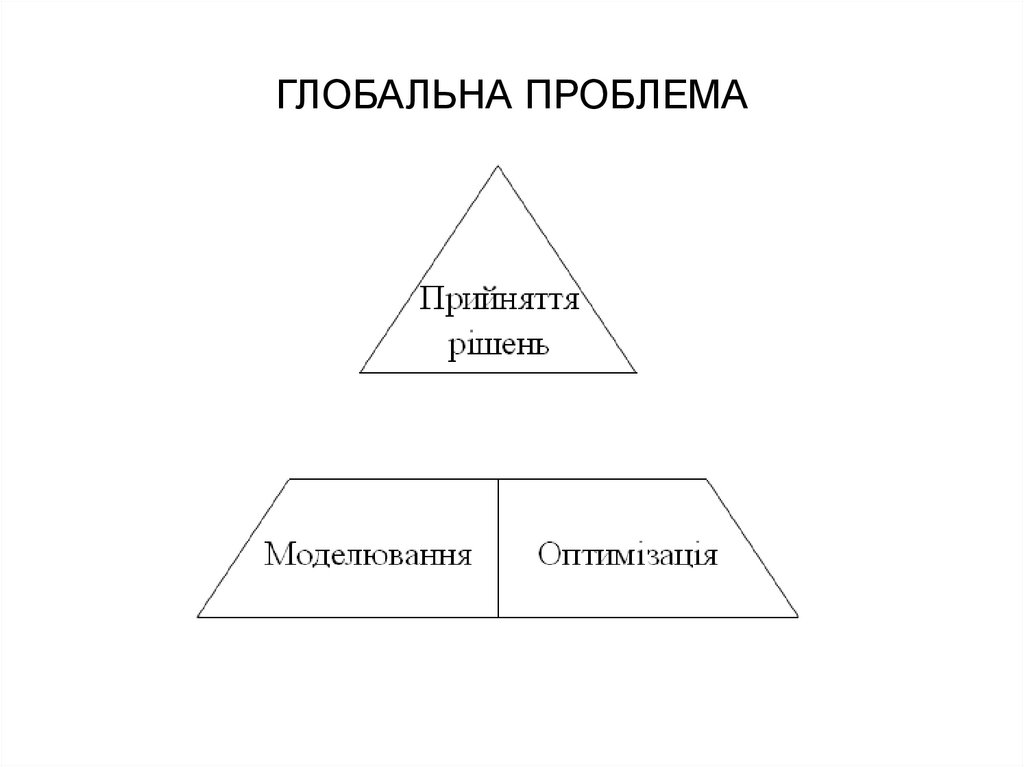
6. ГЛОБАЛЬНА ПРОБЛЕМА

7. ПІДХОДИ ДО ВИРОБЛЕННЯ РІШЕНЬ

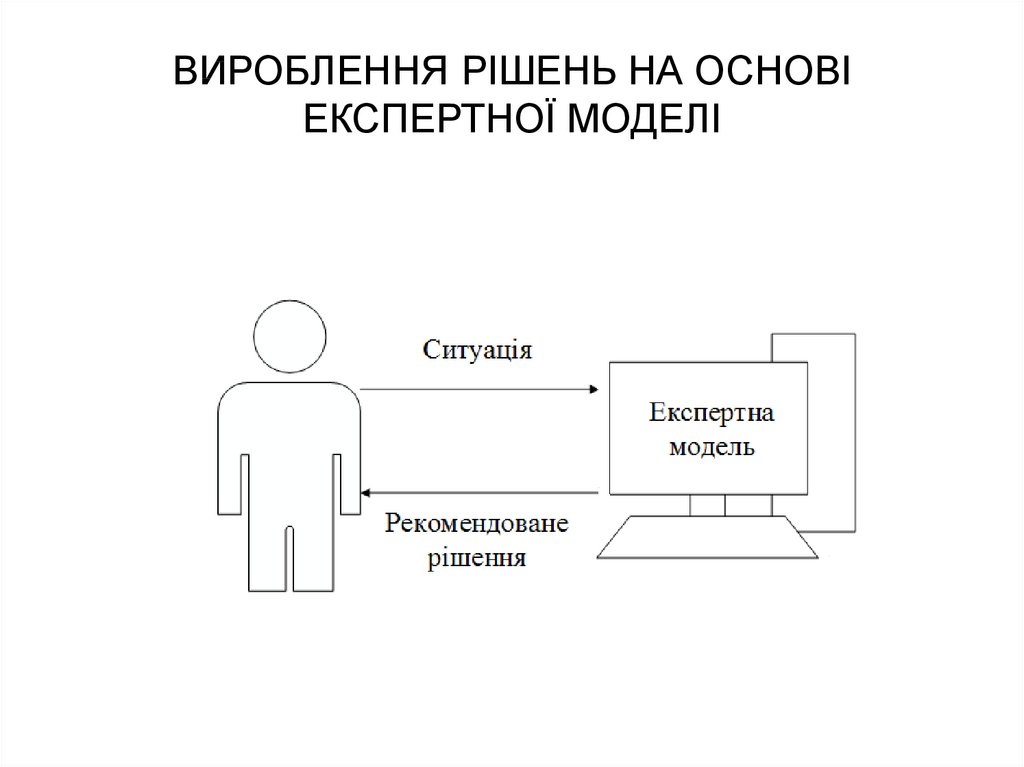
Основа:
• Математична модель задачі прийняття
рішень (ЗПР);
• Імітаційна модель керованого процесу
(системи);
• Експертна модель прийняття рішень.

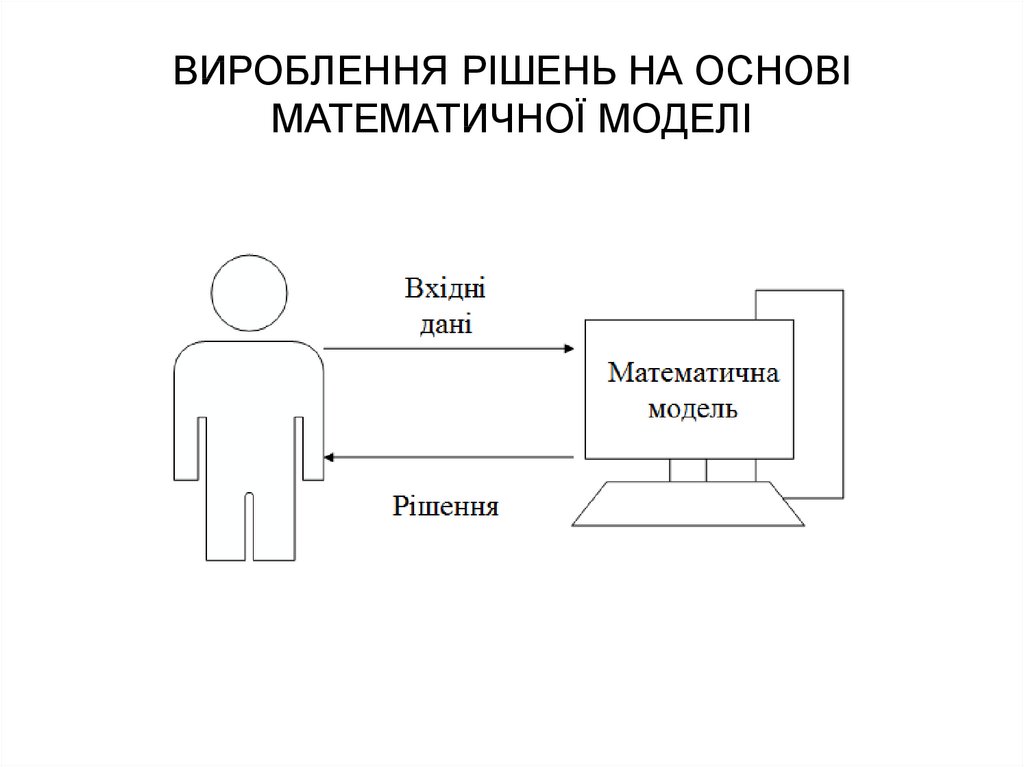
8. ВИРОБЛЕННЯ РІШЕНЬ НА ОСНОВІ МАТЕМАТИЧНОЇ МОДЕЛІ

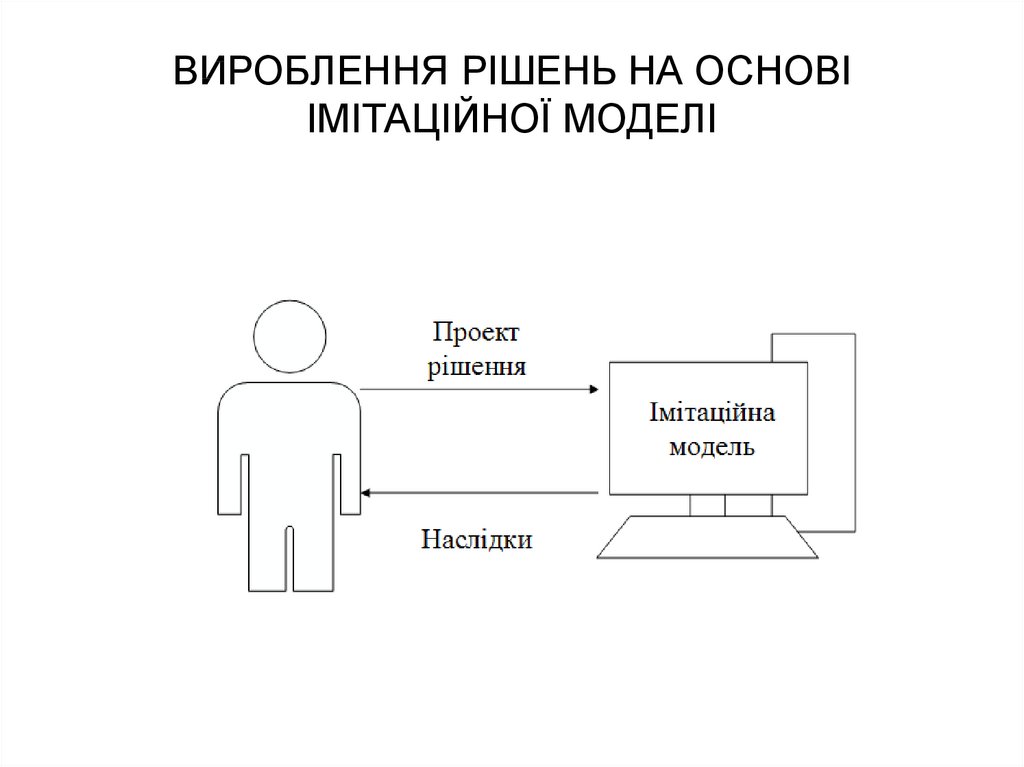
9. ВИРОБЛЕННЯ РІШЕНЬ НА ОСНОВІ ІМІТАЦІЙНОЇ МОДЕЛІ

10. ВИРОБЛЕННЯ РІШЕНЬ НА ОСНОВІ ЕКСПЕРТНОЇ МОДЕЛІ

11. 1. Основні поняття теорії моделювання

• Модель - опис об'єкту на формальній мові, що
дозволяє виводити судження про його властивості і
поведінку за допомогою формальних процедур.
• Моделювання - вивчення властивостей реальних
об'єктів шляхом побудови і дослідження їх моделей.
Адекватність
Види моделювання:
- аналітичне;
- імітаційне.

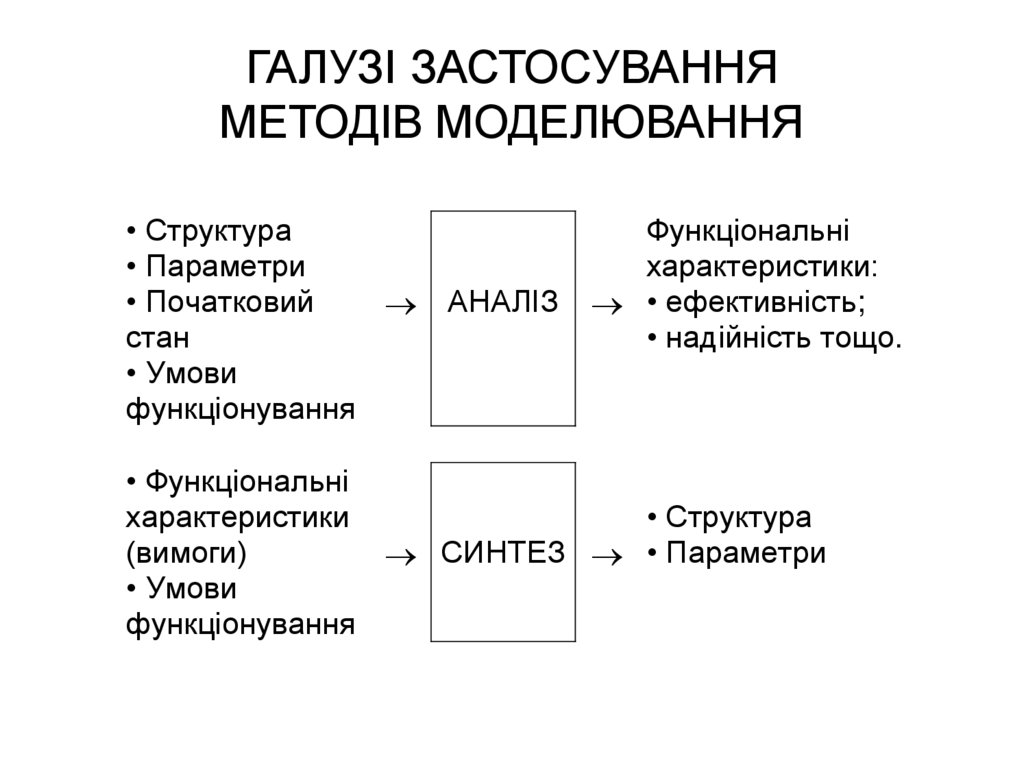
12. ГАЛУЗІ ЗАСТОСУВАННЯ МЕТОДІВ МОДЕЛЮВАННЯ

• Структура
• Параметри
• Початковий
стан
• Умови
функціонування
АНАЛІЗ
Функціональні
характеристики:
• ефективність;
• надійність тощо.
• Функціональні
характеристики
• Структура
(вимоги)
СИНТЕЗ • Параметри
• Умови
функціонування

13. ІМІТАЦІЙНЕ МОДЕЛЮВАННЯ

– реалізація моделюючого алгоритму, який формально
відтворює процес функціонування реального об'єкту.
Елементарні явища, що становлять цей процес,
імітуються із збереженням логічної структури їх
взаємодії та послідовності протікання в часі.
Випадкові явища імітуються за допомогою випадкових
чисел з необхідними імовірнісними характеристиками.
Отримання об'єктивних і стійких характеристик
модельованого процесу потребує його багатократне
відтворення для різних початкових даних з наступною
статистичною обробкою отриманих результатів.

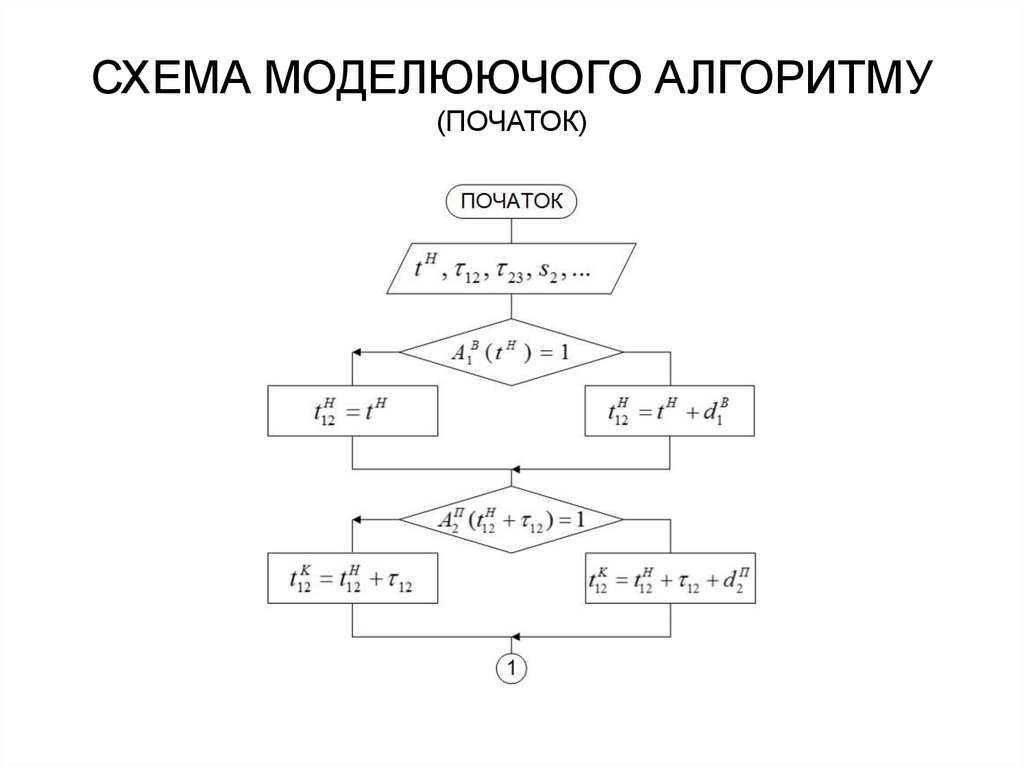
14. ПРИКЛАД ІМІТАЦІЙНОГО МОДЕЛЮВАННЯ

Процес, що моделюється – виконання рейсу за
маршрутом A1 A2 A3 .
Вхідні дані:
t H – час початку рейсу;
12 , 23 – тривалість польоту на дільницях ( A1 A2 ) та
( A2 A3 ) ;
s2 – тривалість стоянки в аеропорту A2 ;
p1B , p2П , p2B , p3П – вірогідності того, що аеропорти будуть
закриті у потрібний час для зльоту ( piB ) або посадки
( piП ) ;
d1B , d 2П , d 2B , d 3П – тривалість закриття аеропортів для
зльоту ( d iB ) або посадки ( d iП ) .
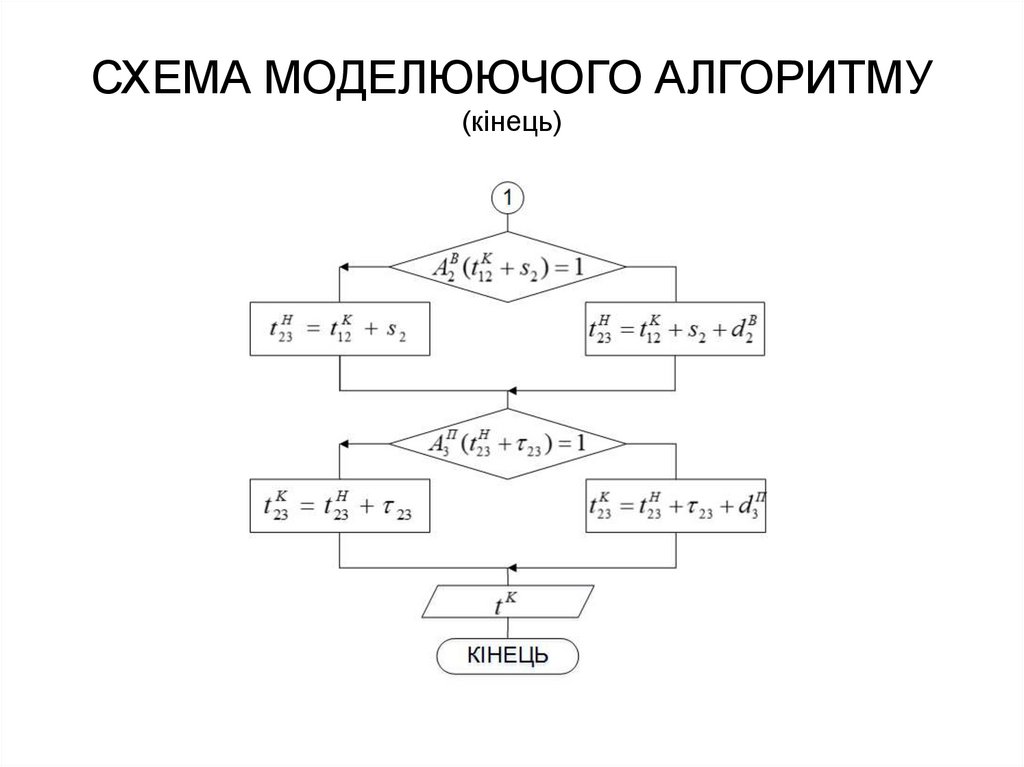
Визначити час завершення рейсу t K .

15. СХЕМА МОДЕЛЮЮЧОГО АЛГОРИТМУ (ПОЧАТОК)

16. СХЕМА МОДЕЛЮЮЧОГО АЛГОРИТМУ (кінець)

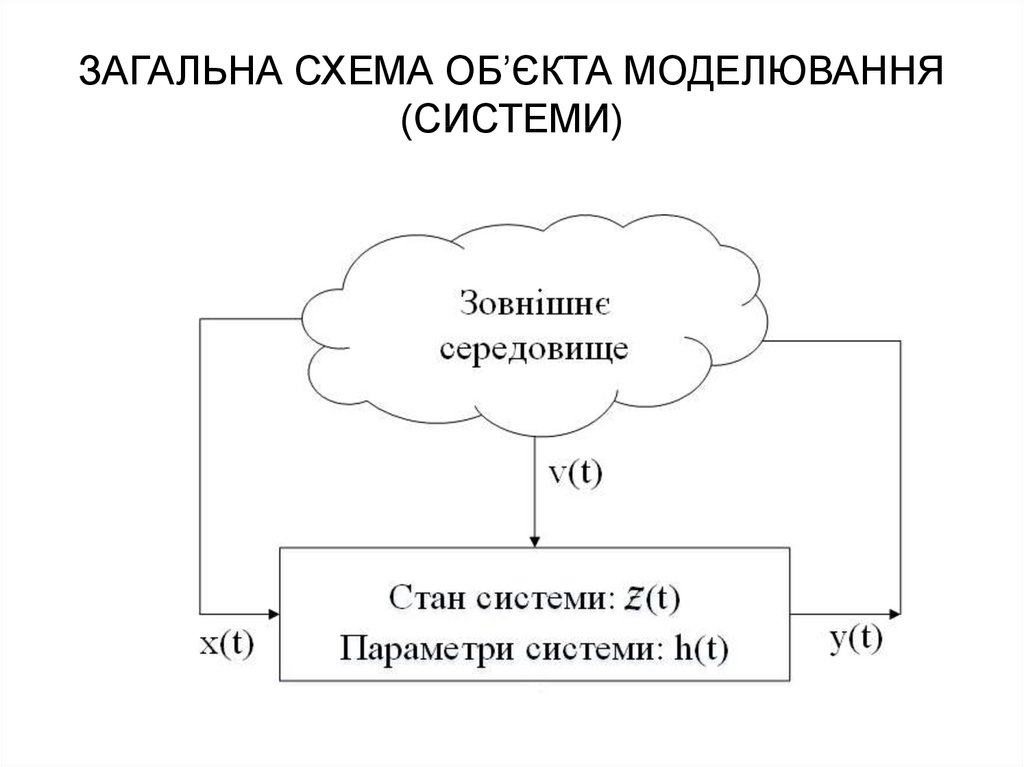
17. ЗАГАЛЬНА СХЕМА ОБ’ЄКТА МОДЕЛЮВАННЯ (СИСТЕМИ)

18. ФОРМАЛЬНИЙ ОПИС СИСТЕМИ (1)

Час: t T ; t0 min { t T }
Поточний стан системи:
z(t ) ( z1 (t ), z2 (t ), ..., zn (t )) Z
Початковий стан системи:
z0 ( z01 , z02 ,..., z0n ) ; z0 j z j (t0 ); j 1, n
Вхідний сигнал:
x(t ) ( x1 (t ), x2 (t ), ... , xm (t )) X
Збурюючі дії:
v(t ) (v1 (t ), v2 (t ), ... , vk (t )) V
Внутрішні (власні) параметри:
h(t ) (h1 (t ), h2 (t ), ... , hl (t )) H

19. ФОРМАЛЬНИЙ ОПИС СИСТЕМИ (2)

Стан системи в момент часу t * T ; t * t 0 :
z (t ) F [ t , z0 , x(t ), h(t ), v(t ) ]
Вихідний сигнал:
y(t ) ( y1 (t ), y2 (t ), ... , yr (t )) Y
t*
t0
*
y (t ) G[ t , z0 , x(t ), h(t ), v(t ) ]
*
t*
t0
y (t ) G[ t , z (t ) ]
Формальна модель системи:
M (T , H , X , V , Z , Y , F , G )
t*
t0
ЗАДАЧА ІМІТАЦІЙНОГО МОДЕЛЮВАННЯ:
побудова функцій z (t ) та y (t ) , t T .

20. 2. Моделювання випадкових явищ

Імовірнісні характеристики випадкової величини
рівномірно розподіленої в інтервалі [0, 1]:
1, якщо 0 x 1
f ( x)
0, якщо x 0 або x 1
0, при x 0
F ( x) x, при 0 x 1
1, при x 1
1
M ( ) x f ( x) dx
0
1
2
1
D( ) [ x M ( )]2 f ( x) dx
0
( ) D( )
1
2 3
1
12
,

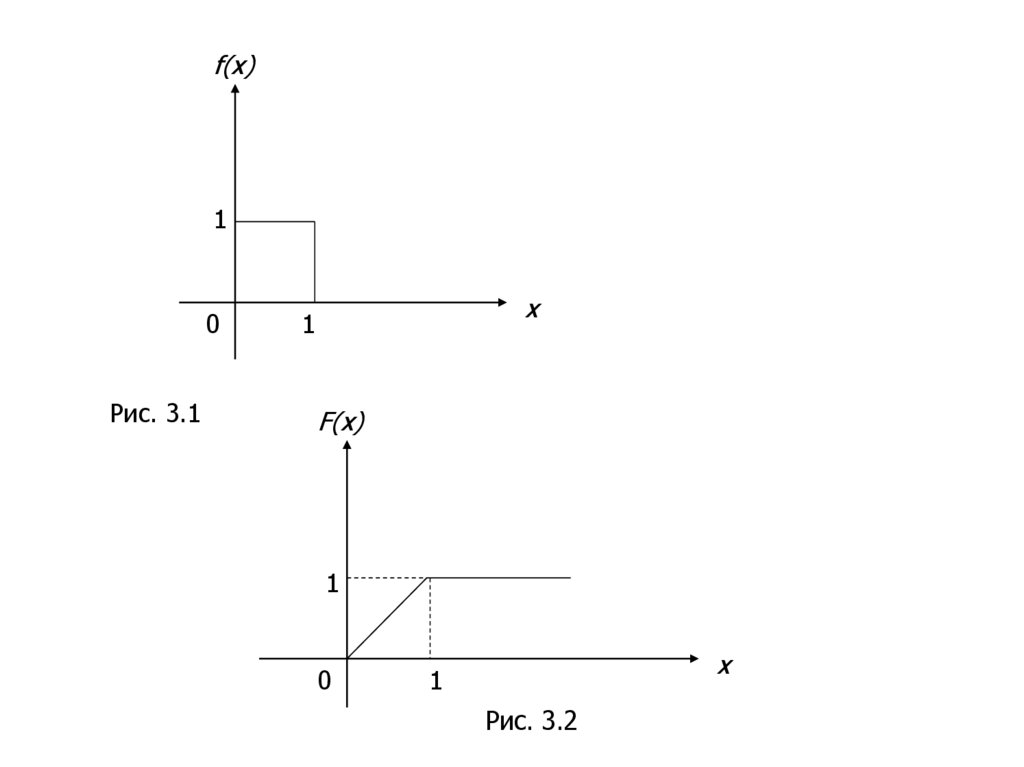
21.

f(x)
1
0
Рис. 3.1
x
1
F(x)
1
0
x
1
Рис. 3.2

22. ПРЕДСТАВЛЕННЯ ЗНАЧЕНЬ

випадкової величини [0, 1]
в цифрових обчислювальних системах
z1 2 1 z2 2 2 ... zn 2 n ;
n – кількість двійкових розрядів;
zk {0, 1} з вірогідністю ½; k 1, n .
m
;
xi n
2 1
m {0, 1, 2, ... ,2 n 1} ; i 1, 2, ... ;
pi
1
.
n
2

23. ІМОВІРНІСНІ ХАРАКТЕРИСТИКИ

дискретної випадкової величини , квазірівномірно
розподіленої в інтервалі [0, 1]:
2 n 1
m
1
2n 1 2n ;
m 0
N
N ( N 1)
1
/
m
;
M
(
)
2
2
m 1
M ( / )
2
1 2 1 m
1
D ( ) n n
;
2 m 0 2 1 2
N
N ( N 1)(2 N 1)
1 2n 1
2
/
;
D( )
n
m
6
12 2 1
m 1
n
/
( )
/
1
2 3
2n 1
.
n
2 1

24. СПОСОБИ формування послідовностей випадкових чисел, рівномірно розподілених в інтервалі [0,1]

- апаратний (фізичний);
- табличний (файловий);
- алгоритмічний (програмний):
xi 1 ( xi , xi 1 , ... , x0 )

25. АЛГОРИТМІЧНІ МЕТОДИ формування послідовностей псевдовипадкових чисел в інтервалі [0,1]

• мультиплікативний метод (метод
вирахувань);
• метод підсумовування;
• метод усікання;
• метод перемішування.

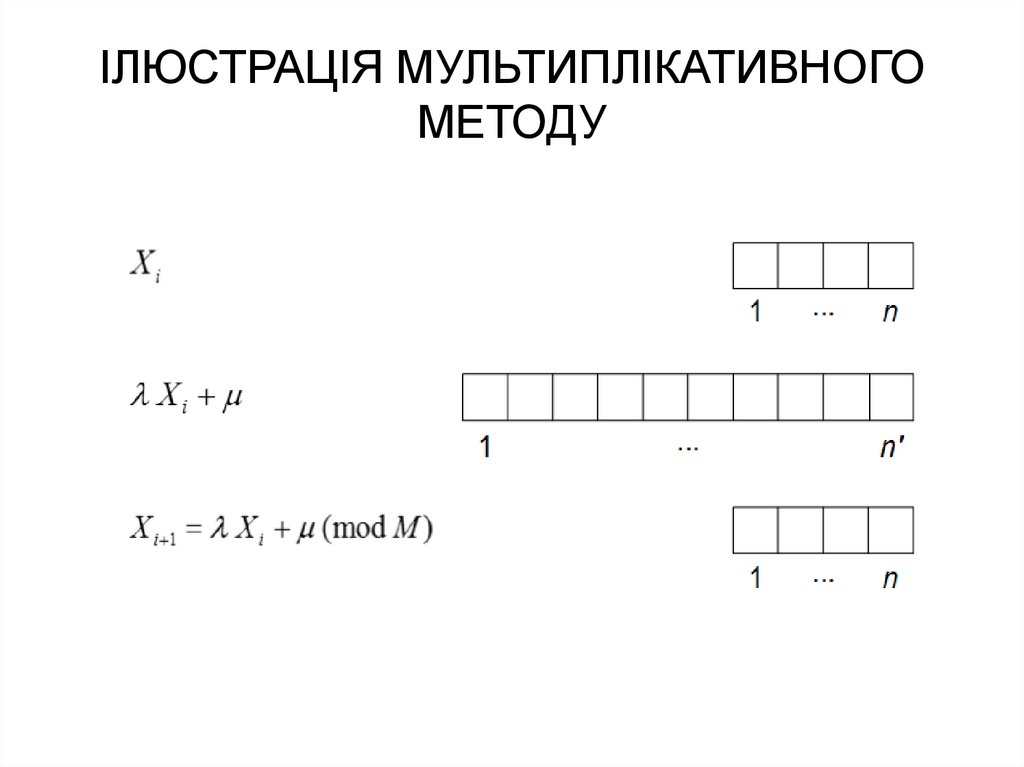
26. МУЛЬТИПЛІКАТИВНИЙ МЕТОД

X i 1 X i (mod M ) ;
X i 1 X i (mod M ) ;
X
xi 1 i 1 ;
M
n
M q 1 ; 8 3 ,
q – основа системи числення, прийнятої в комп'ютері;
n – кількість цифрових розрядів в машинному слові;
– ціле позитивне число;
– ціле позитивне непарне число;
X 0 – ціле позитивне непарне число.
Період послідовності: 106 1011 .

27. ІЛЮСТРАЦІЯ МУЛЬТИПЛІКАТИВНОГО МЕТОДУ

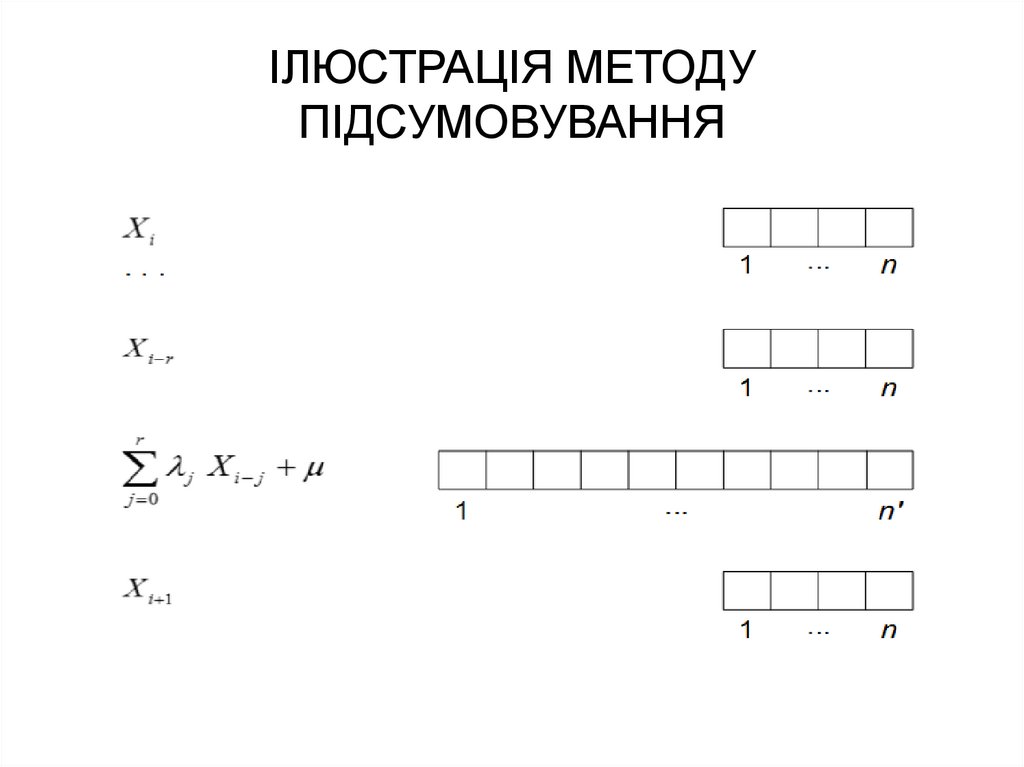
28. МЕТОД ПІДСУМОВУВАННЯ

r
X i 1 j X i j (mod M ); i r ;
j 0
xi 1
X i 1
;
M
r , j , X i , , M – цілі позитивні числа;
X r , X r 1 , ... , X 0 – випадкові числа з діапазону (0, M ) .
Період послідовності: 109 1017 .

29. ІЛЮСТРАЦІЯ МЕТОДУ ПІДСУМОВУВАННЯ

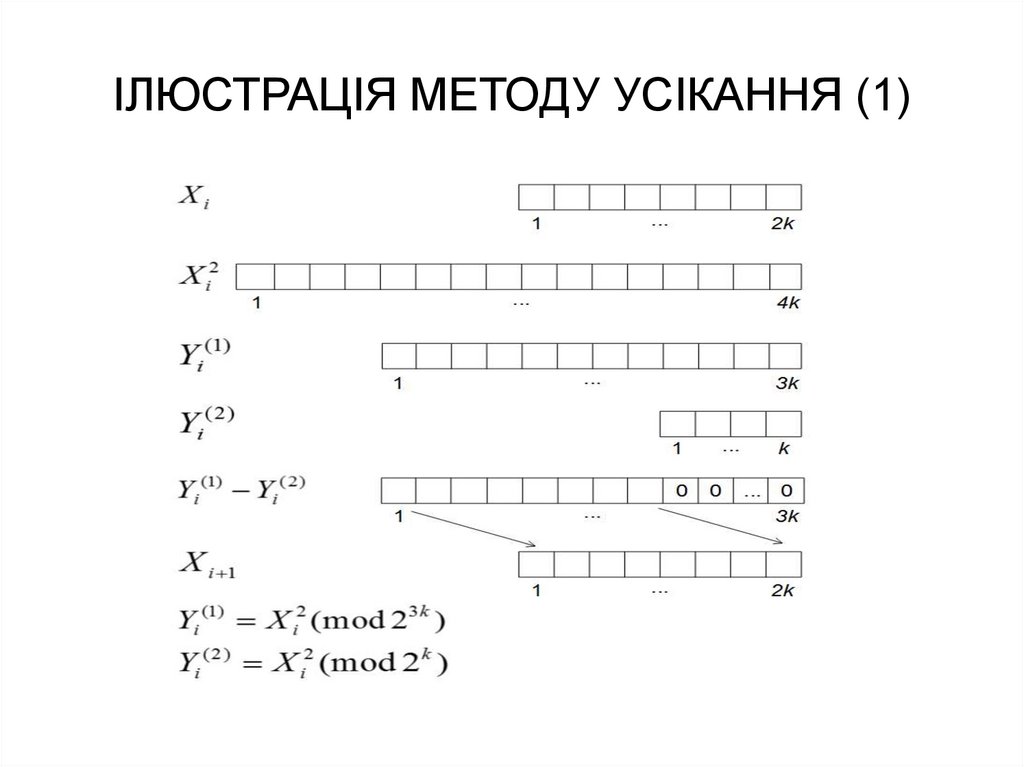
30. МЕТОД УСІКАННЯ

X i 1 { X i2 (mod 23 k ) X i2 (mod 2k )}2 k ;
X i 1 { X i X i 1 (mod 23 k ) X i X i 1 (mod 2k )}2 k ;
X i 1 [{ X i2 (mod 22 k )}C 2 2 k ] [ X i2 2 2 k ]C (mod 22 k ).
2k – кількість двійкових розрядів;
C const ;
[…] – ціла частина числа;
– знак порозрядного складання двійкових чисел.
X i 1
xi 1 2 k
2 1

31. ІЛЮСТРАЦІЯ МЕТОДУ УСІКАННЯ (1)

32. ІЛЮСТРАЦІЯ МЕТОДУ УСІКАННЯ (2)

33. ПРОГРАМНІ ЗАСОБИ

формування послідовностей
псевдовипадкових чисел
C++:
double result=min+double(rand()) / RAND_MAX * (max - min);
C#:
double result=min+randomNumber.NextDouble()*(max-min);
Java:
double result=min+Math.random()*(max-min);

34. ПЕРЕВІРКА ЯКОСТІ

послідовностей псевдовипадкових чисел,
отриманих алгоритмичними методами
• Тест частот – перевірка рівномірності
розподілу псевдовипадкових чисел в
інтервалі [0, 1].
• Тест пар – перевірка незалежності
псевдовипадкових чисел.

35. Карл Пірсон (27.03.1857 – 27.04.1936)

• Професор прикладної
математики і механіки
Лондонського
університетського коледжу.
Професор геометрії Грэшемколеджу. Член Королівського
Товариства. Почесний доктор
наук Лондонського
університету. Почесний член
Кембріджського
Королівського коледжу,
Едінбурзького Королівського
Товариства, Лондонського
університетського коледжу.

36. ТЕСТ ЧАСТОТ (1)

( xi ; i 1, N ) – послідовність псевдовипадкових
чисел;
m – кількість рівних напіввідкритих інтервалів на
відрізку (0, 1).
N j – емпірічна частота j 1, m .
Вірогідність попадання числа xi в j -й інтервал:
1
p j ; j 1, m .
m
Теоретична частота:
N
*
N j p j N ; j 1, m .
m

37. ТЕСТ ЧАСТОТ (2)

Критерій Пірсона:
m
2
j 1
(N j N )
* 2
j
N
*
j
m
N
m
j 1
2
N
Nj .
m
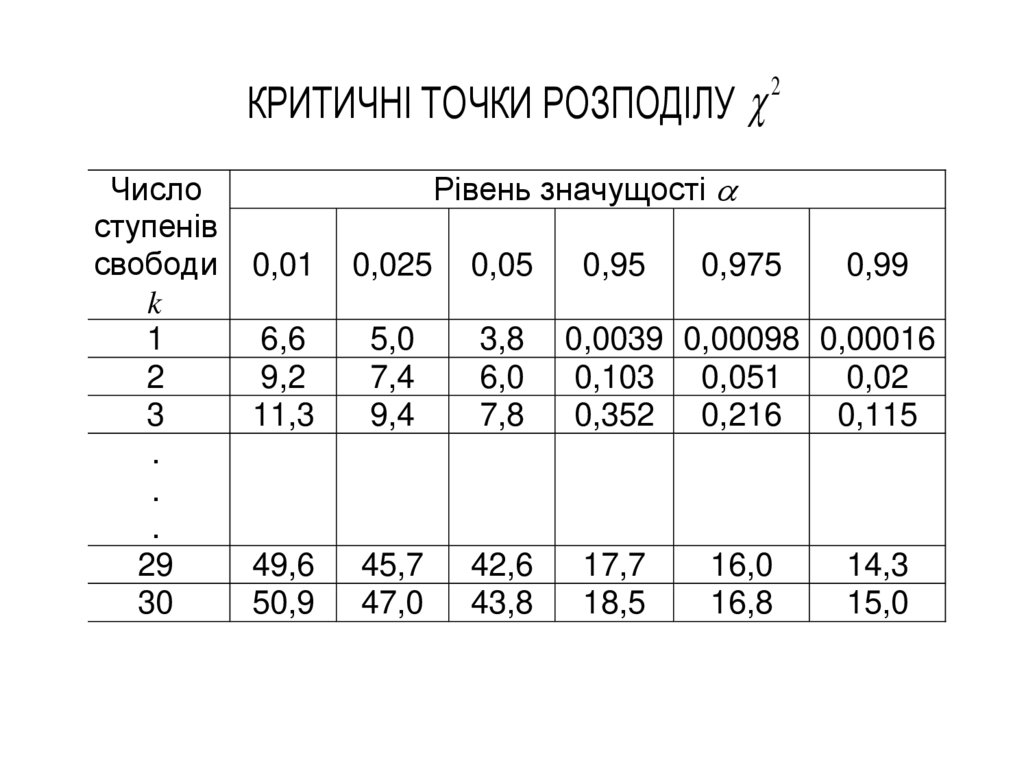
Гіпотеза приймається, якщо
2 кр2 ( , k ) ,
2
k – кількість ступенів свободи розподілу : k m 1;
– рівень значущості.

38.

КРИТИЧНІ ТОЧКИ РОЗПОДІЛУ
Число
ступенів
свободи
k
1
2
3
.
.
.
29
30
2
Рівень значущості
0,01
0,025
0,05
6,6
9,2
11,3
5,0
7,4
9,4
3,8
6,0
7,8
49,6
50,9
45,7
47,0
42,6
43,8
0,95
0,975
0,99
0,0039 0,00098 0,00016
0,103 0,051
0,02
0,352 0,216
0,115
17,7
18,5
16,0
16,8
14,3
15,0

39. ТЕСТ ПАР

Способи формування пар псевдовипадкових чисел:
( x1 , x2 ); ( x3 , x4 ); ( x5 , x6 ); ...;
Кількість пар N / 2 .
( x1 , x2 ); ( x2 , x3 ); ( x3 , x4 ); ...;
Кількість пар N .

40. ТЕСТ ПАР (1 спосіб)

– емпірічна частота попадання пар чисел в
N jl
клітини квадратної таблиці розмірності m m ; j 1, m ;
l 1, m .
Вірогідність попадання пари чисел в ( j , l ) -у клітину
таблиці:
1
p jl 2 ; j 1, m; l 1, m .
m
Теоретична частота попадання пар чисел в клітини
таблиці:
N
1
N
N
.
N *jl p jl
2
2
m
2
2m 2
Критерій Пірсона:
N
*
2m 2 m
jl N jl
*
N jl
N j 1
2
2
N
N
jl 2m 2 .
j 1 l 1
l 1
2
Кількість ступенів свободи розподілу :
2
m
m
k m ( m 1) .
Гіпотеза приймається, якщо
2 кр2 ( , k ) .
m

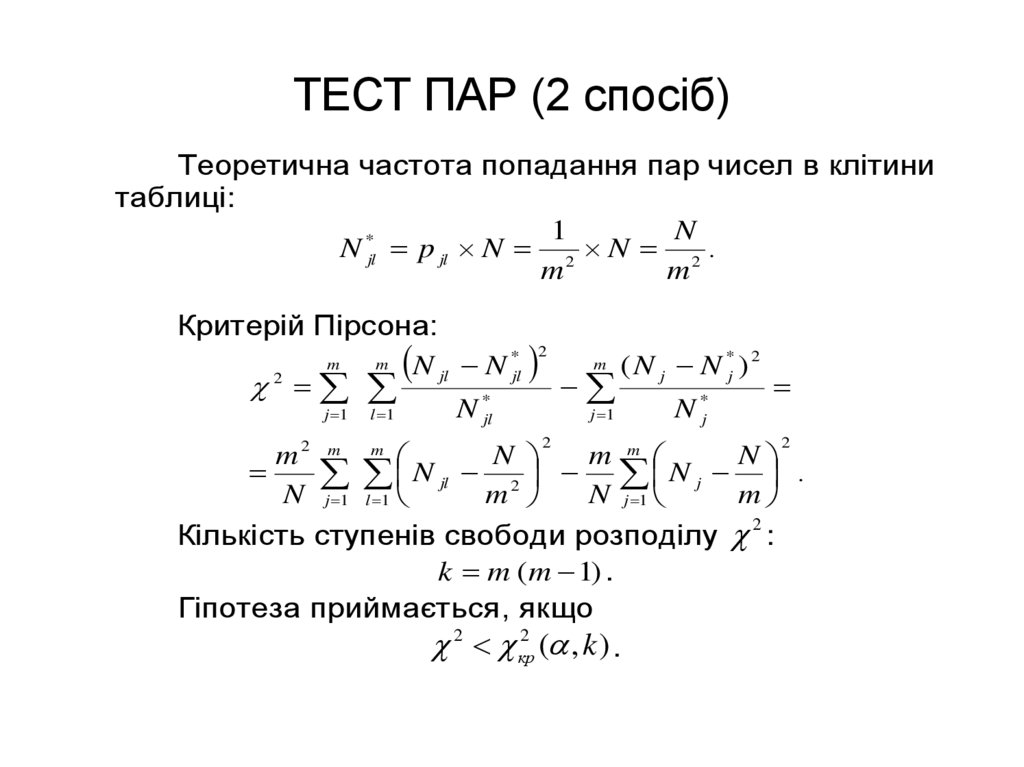
41. ТЕСТ ПАР (2 спосіб)

Теоретична частота попадання пар чисел в клітини
таблиці:
N
1
N *jl p jl N 2 N 2 .
m
m
Критерій Пірсона:
* 2
* 2
m (N N )
m N
m
N
j
j
2 jl * jl
*
Nj
N jl
j 1
j 1 l 1
2
N
m m
N
m2 m m
N
N
jl m 2 N j m
N j 1 l 1
j 1
2
Кількість ступенів свободи розподілу :
k m (m 1) .
Гіпотеза приймається, якщо
2 кр2 ( , k ) .
2
.

42. МОДЕЛЮВАННЯ ВИПАДКОВОЇ ПОДІЇ

Дано: вірогідність p настання випадкової події A .
Вважатимемо, що подія A сталася, якщо
xi p .
Доведення:
p
p
0
0
P( xi p) f ( x) dx dx p .

43. МОДЕЛЮВАННЯ ГРУПИ ВИПАДКОВИХ ПОДІЙ

p1 , p 2 , ... , p j , ... , p n
настання
вірогідності
Дано:
неспільних випадкових подій A1 , A2 , ... , A j , ... , An , що
утворюють повну групу:
n
pj
1.
j 1
Відрізок (0, 1) розбивається на n напіввідкритих
інтервалів, довжина яких дорівнює вірогідностям
p j , j 1, n .
Межі j -го відрізку:
l 0 0;
j
lj pj;
j 1, n .
r 1
Вважатимемо, що сталася подія Am , якщо lm 1 xi lm .
Доведення:
P(lm 1 xi lm )
lm
f ( x) dx lm lm 1 pm
lm 1

44. МОДЕЛЮВАННЯ ЗАЛЕЖНИХ ВИПАДКОВИХ ПОДІЙ (спосіб 1)

Дано: вірогідності p( A) і p(B) настання
залежних
випадкових подій A і B ; умовна вірогідність p( B / A) .
1. Перевіряється справедливість нерівності
(3.1)
xi p( A) .
2.
Якщо
(3.1)
виконується,
перевіряється
справедливість нерівності
xi 1 p( B / A) .
3. Якщо (3.1) не виконується, визначається умовна
вірогідність p ( B / A) , виходячи з формули повної
вірогідності
p ( B) p ( A) p ( B / A) p ( A) p ( B / A) :
p( B / A)
p( B) p( A) p( B / A)
.
1 p( A)
4. Перевіряється справедливість нерівності
xi 1 p( B / A) .

45. МОДЕЛЮВАННЯ ЗАЛЕЖНИХ ВИПАДКОВИХ ПОДІЙ (спосіб 2)

Складні події AB , AB , AB і A B розглядаються як
неспільні випадкові події, що становлять повну групу.
Вірогідність їх настання:
p ( AB ) p ( A) p ( B / A);
p ( AB) p ( A)[1 p ( B / A)];
p ( AB) [1 p ( A)] p ( B / A);
p ( AB) [1 p ( A)][1 p ( B / A)] ,
причому
p ( AB ) p ( AB) p ( AB) p ( AB) 1.
Застосовується процедура моделювання неспільних
подій, що становлять повну групу.

46. Марков Андрій Андрійович (1856-1922)

- російський математик,
професор Санкт-Петербурзького
університету,
академік Імператорської
Санкт-Петербурзької академії наук.
Вніс великий вклад до теорії
ймовірностей, математичного
аналізу і теорії чисел.
Є першовідкривачем великого
класу стохастичних процесів з
дискретним і неперервним
часом, названих його ім'ям.

47. ПОНЯТТЯ МАРКІВСЬКОГО ЛАНЦЮГА

Марківський випадковий процес: для кожного моменту
часу t ймовірність будь-якого стану системи (об'єкту
моделювання) у майбутньому (при t t ) залежить
тільки від її стану у теперішньому (при t t ) і не
залежить від того, коли і яким чином система прийшла
в цей стан.
Марківський випадковий процес з дискретними
станами і дискретним часом – дискретний марківський
ланцюг (стохастичний автомат, імовірнісний автомат,
P -схема, P -модель).
Відмітні особливості дискретних марківських ланцюгів:
• простір станів системи є кінцевою множиною
Z { zi i 1, m } ;
• переходи системи із стану в стан можливі тільки в
строго визначені, заздалегідь фіксовані моменти часу
t1 , t2 , t3 ,...

48. МОДЕЛЮВАННЯ МАРКІВСЬКИХ ЛАНЦЮГІВ (1)

Дано:
1) вектор вірогідностей початкових станів системи
( pk (0), k 1, n) :
n
pk (0) 1 ;
k 1
2) матриця переходів:
p11
p
P 21
.
pn1
n
p jk
k 1
p12
. . .
p22
.
. . .
. . .
pn 2
. . .
1;
p1n
p2 n
;
.
pnn
j 1, n .

49. МОДЕЛЮВАННЯ МАРКІВСЬКИХ ЛАНЦЮГІВ (2)

1. Визначення початкового стану системи.
Розбиття відрізка (0,1) на n напіввідкритих інтервалів:
l0 0 ;
k
lk pr (0) ;
k 1, n .
r 1
Якщо lk * 1 xi lk * , вважаємо, що початковим станом
системи є z (0) zk * .
2. Визначення наступних станів системи.
Фіксація номеру рядка матриці переходів: j * k * .
Розбиття відрізка (0,1) на n напіввідкритих інтервалів:
k
l j * ,0 0 ; l j * , k p j * , r ;
k 1, n .
r 1
Якщо l j * , k * 1 xi m l j * , k * , вважаємо, що станом системи
на m -у етапі моделювання є z (m) z k * .

50. МОДЕЛЮВАННЯ ВИПАДКОВИХ ВЕЛИЧИН

Дано: послідовність випадкових чисел ( xi ) – значень
випадкової величини , розподіленої з постійною
щільністю f (x) в інтервалі [0, 1].
Визначити: послідовність значень ( y j ) випадкової
величини , розподіленої з функцією щільності f ( y ) на
відрізку числової осі (a, b) .

51. МОДЕЛЮВАННЯ ДИСКРЕТНИХ ВИПАДКОВИХ ВЕЛИЧИН

– випадкова величина, яка може набувати
значень y1 , y2 , ... , yn з вірогідністями p1 , p2 , ... , pn :
n
p j 1.
j 1
Визначення її значень зводиться до моделювання
групи неспільних подій A1 , A2 , ... , An .
Подія A j полягає в тому, що випадкова величина
набуває значення y j ; j 1, n .

52. МЕТОДИ МОДЕЛЮВАННЯ БЕЗПЕРЕРВНИХ ВИПАДКОВИХ ВЕЛИЧИН

• прямого перетворення (зворотній
функції);
• кускової апроксимації функції щільності;
• відсіювання (виключення);
• моделювання умов граничних теорем
теорії ймовірностей.

53. МЕТОД ПРЯМОГО ПЕРЕТВОРЕННЯ

Теорема: якщо випадкова величина має щільність
розподілу f ( y ) , то розподіл випадкової величини
f ( y)dy
є рівномірним в інтервалі числової осі (0,1).
yj
Чергове
число
обчислюється
шляхом
розв’язання такого рівняння відносно верхньої межі
інтегрування:
yj
f ( y)dy xi

54. ПРИКЛАД ЗАСТОСУВАННЯ МЕТОДУ ПРЯМОГО ПЕРЕТВОРЕННЯ

f ( y ) e y ; y 0 .
yj
e y dy xi ;
0
yj
1 y
e xi ;
0
1 e
y j
xi ;
1
1
y j ln(1 xi ) або y j
ln xi .

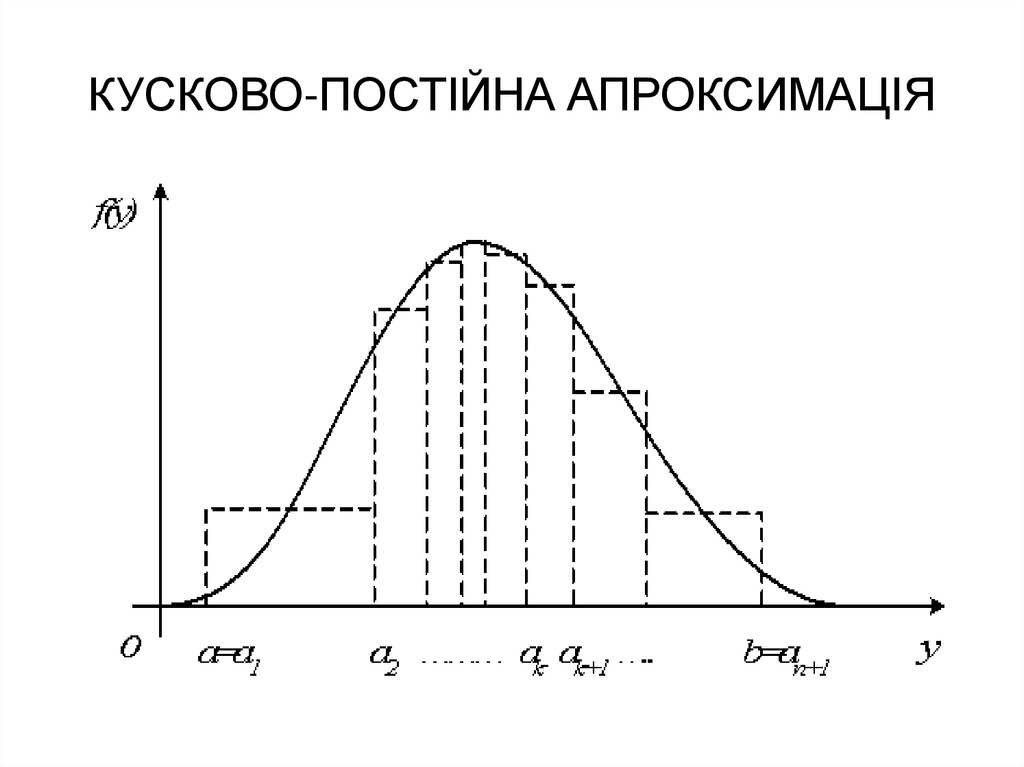
55. МЕТОД КУСКОВОЇ АПРОКСИМАЦІЇ

Відрізок (a, b) розбивається на n частин (ak , ak 1 ]:
a k 1
1
; k 1, n .
dy
)
y
(
f
n
ak
На кожному напіввідкритому інтервалі (ak , ak 1 ]
функція щільності f ( y ) апроксимується постійною або
лінійною функцією k ( y) , k 1, n .
y j ak j z j ;
k j n xi ; 0 z j ak j 1 ak j ;
zj
k
0
j
( y )dy xi 1 .

56. КУСКОВО-ПОСТІЙНА АПРОКСИМАЦІЯ

57.

ОБЧИСЛЕННЯ z j
ПРИ КУСКОВО-ПОСТІЙНІЙ АПРОКСИМАЦІЇ
k ( y) k*
1
const ; k 1, n ;
ak 1 ak
zj
1
a a dy xi 1 ;
0 k 1
k
y
a k 1 a k
zj
xi 1 ;
0
zj
ak 1 ak
xi 1 ;
z j (ak j 1 ak j ) xi 1 .
y j ak j (ak j 1 ak j ) xi 1 .

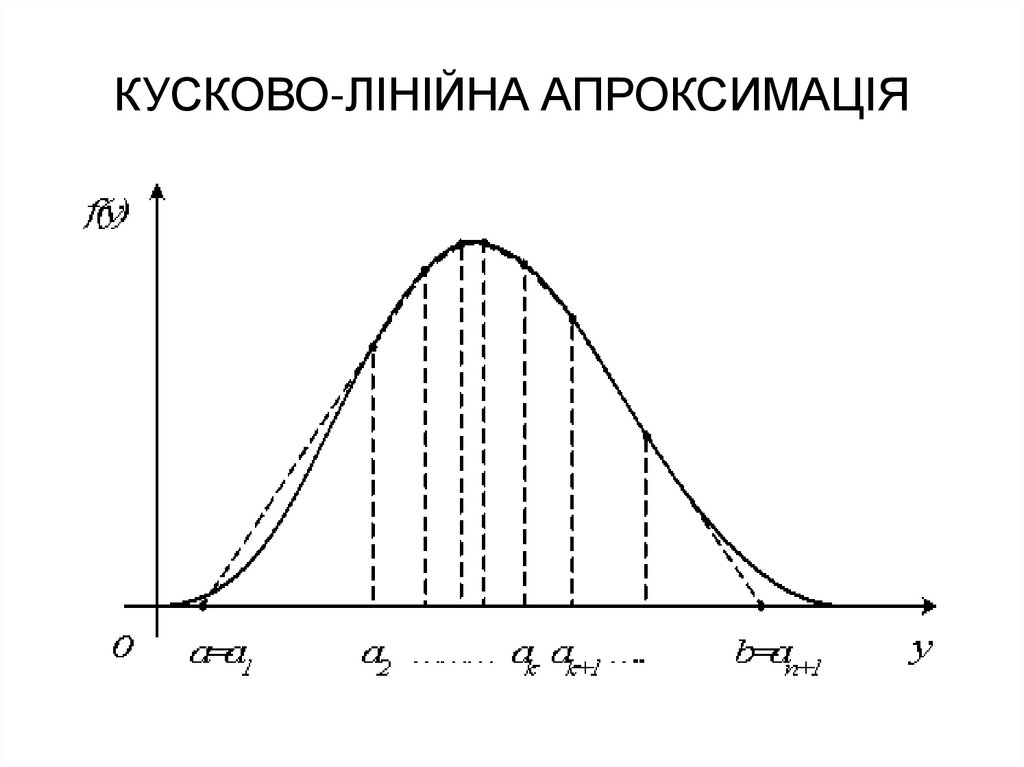
58. КУСКОВО-ЛІНІЙНА АПРОКСИМАЦІЯ

59.

ОБЧИСЛЕННЯ z j
ПРИ КУСКОВО-ЛІНІЙНІЙ АПРОКСИМАЦІЇ
k ( y) k y k ; k 1, n ;
f k 1 f k
1
*
k
( f k 1 f k ) , f k f (ak ) ;
;
k
k
ak 1 ak
2
zj
( k y k )dy xi 1 ;
k
2
y2 k y
0
zj
k
xi 1 ;
2
0
zj
k j
kj
y j ak j
k j
kj
1
2
k2j 2 k j xi 1 .
kj
z j k z j xi 1 0 ;
1
kj
k2j 2 k j xi 1 .

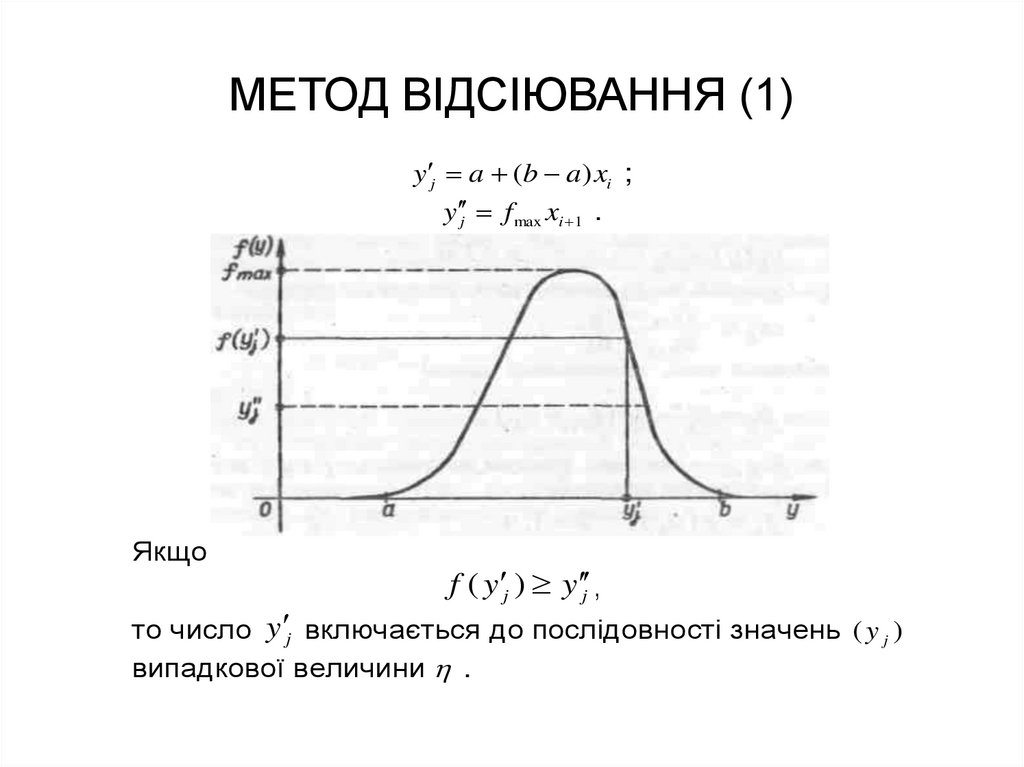
60. МЕТОД ВІДСІЮВАННЯ (1)

y j a (b a ) xi ;
y j f max xi 1 .
Якщо
f ( y j ) y j ,
то число y j включається до послідовності значень ( y j )
випадкової величини .

61. МЕТОД ВІДСІЮВАННЯ (2)

Доведення:
P(c d ) P[c y j d f ( y j ) y j ] ,
c a ; d b.
A – випадкова подія: f ( y j ) y j ;
B – випадкова подія: c y j d .
p( AB ) p( A) p( B / A) ; p( B / A)
P[ f ( y j ) y j ]
f ( y )
f ( y )dy
0
d
P(c y j d ) f ( y )dy .
c
1
b a
0
1
f max
d y
p( AB )
.
p( A)
1
;
f max (b a )

62. МЕТОД ВІДСІЮВАННЯ (3)

P[c y j d f ( y ) y j ]
P[(c y d ) & ( f ( y ) y )]
P[ f ( y ) y ]
d
f ( y)dy
c
1
f max (b a)
1
f max (b a)
d
f ( y )dy
c

63. МОДЕЛЮВАННЯ НОРМАЛЬНОГО РОЗПОДІЛУ (1)

Сформувати послідовність випадкових чисел ( y j ) ,
що мають нормальний розподіл з математичним
очікуванням a і середнім квадратичним відхиленням
:
( y a) 2
1
.
f ( y)
exp
2
2
2
Центральна гранична теорема: якщо 1 , 2 , ..., n –
незалежні однаково розподілені випадкові величини,
що мають математичне очікування a( ) і середнє
квадратичне відхилення ( ) , то сума
n
i
i 1
асимптотично нормальна з математичним очікуванням
a( ) n a( )
і середнім квадратичним відхиленням
( ) n ( ) .

64. ФОРМУВАННЯ НОРМОВАНОЇ ВЕЛИЧИНИ

Якщо i xi ; i 1, n , то:
1 n
1
n
( ) n ; ( ) n
.
2 2
2 3 2 3
Якщо i 2 xi 1 ; i 1, n , то:
1
1
1
a ( i ) 2 1 0 ; ( i ) 2
;
2
2 3
3
1
n
( ) n 0 0 ; ( ) n
.
3
3
Нормована величина:
3 n
u
(2 xi 1) ;
( )
n i 1
a(u ) 0 ;
(u) 1 .

65. МОДЕЛЮВАННЯ НОРМАЛЬНОГО РОЗПОДІЛУ (2)

yj uj a ;
3 m j n
3 m j n
(2 xi 1)
uj
2 xi n ;
n i m j 1
n i m j 1
v j u j
1
(3u j u 3j ) ;
20n
41
3
5
u
10
u
(
v j u j
j 15u j ) .
j
2
13440n

66. МОДЕЛЮВАННЯ РОЗПОДІЛУ ПУАССОНА

Сформувати послідовність випадкових чисел ( y j ) , що
мають закон розподілу Пуассона з математичним
очікуванням a .
Теорема Пуассона: якщо p – вірогідність настання
випадкової події A при одному випробуванні, то
вірогідність настання k подій в n незалежних
випробуваннях
при
і
p 0
np a
n ,
асимптотично рівна
Pn (k )
Чергове число:
k
k!
yj k.
Рекомендовано: a / n 0,2 .
e .

67. МОДЕЛЮВАННЯ ВИПАДКОВИХ ВЕКТОРІВ (1)

Сформувати послідовність наборів значень координат
випадкового вектору ( , , ) , заданого спільною
функцією щільності f w, y, z .
f1 ( z )
f ( w, y, z ) dw dy ;
f2 ( y / z j )
f ( w, y, z j )
dw ;
f1 ( z j )
f ( w, y j , z j )
f3 ( w / y j , z j )
.
f1 ( z j ) f 2 ( y j / z j )

68. МОДЕЛЮВАННЯ ВИПАДКОВИХ ВЕКТОРІВ (2)

Випадковий
вектор
z ( zi i 1, n ) ,
заданий
кореляційною матрицею
K kij , k ij k ji ; i 1, n; j 1, n
з математичними очікуваннями компонентів ai ; i 1, n .
z1 c11 y1 a a1 ;
z2 c12 y1 a c22 y2 a a2 ;
.................................................................
zn c1n y1 a c2 n y2 a ... cnn yn a an .

69. МОДЕЛЮВАННЯ ВИПАДКОВИХ ВЕКТОРІВ (3)

( yi ; i 1, n)
–
послідовність
некорельованих
випадкових чисел з математичним очікуванням a і
середнім квадратичним відхиленням ;
cij – коефіцієнти, послідовно визначувані з рівнянь
k ij
Приклад:
2
i
cri crj
;
i 1, j ;
j 1, n .
r 1
k11 2 c112 ;
k12 2 c11 c12 ;
2
;
k 22 2 c122 c 22
k13 2 c11 c13 ;
k 23 2 c12 c13 c 22 c 23 ;
2
2
;
k 33 2 c132 c 23
c33
.........................................

70. МОДЕЛЮВАННЯ ВИПАДКОВИХ ФУНКЦІЙ (1)

КОРЕЛЯЦІЙНИЙ ПІДХІД
Дано: (ti ; i 1, n) – послідовність моментів часу;
m(t ) [ m(ti ) ; i 1, n ] – вектор математичних очикувань
випадкової функції z (t ) в кожний з цих моментів;
K k ij – кореляційна матриця, де kij характеризує
залежність значень випадкової функції z (t ) в моменти
часу ti і t j ; i 1, n ; j 1, n .
Необхідно визначити значення випадкової функції z (t )
в моменти часу ti ; i 1, n .
Розв’язання задачі: моделювання випадкового вектору
z (t ) [ z (ti ) ; i 1, n ] .

71. МОДЕЛЮВАННЯ ВИПАДКОВИХ ФУНКЦІЙ (2)

КАНОНІЧНЕ РОЗКЛАДАННЯ
r
z (ti ) m(ti ) v j j (ti ) ; i 1, n ;
j 1
m(ti ) – математичне очікування випадкової функції z (t )
у момент часу ti ;
v j – коефіцієнти розкладання випадкової функції
[некорельовані випадкові величини з довільними
законами розподілу, M (v j ) 0 ]; i 1, n ;
j (t ) – координатні (елементарні детерміновані)
функції; i 1, n .

72. МОДЕЛЮВАННЯ СТАЦІОНАРНИХ ВИПАДКОВИХ ФУНКЦІЙ (1)

m(t ) const ;
K t , t K t t .
s (t1 ) c1 y1 c2 y2 ... cn yn ;
s (t2 ) c1 y2 c2 y3 ... cn yn 1 ;
...................................................
s (ti ) c1 yi c2 yi 1 ... cn yn i 1 ;
....................................................
s (tn ) c1 yn c2 yn 1 ... cn y2 n 1 ,
yi – некорельовані випадкові числа з математичним
очікуванням M ( yi ) 0 і дисперсією 2 ; i 1, 2n 1;
ci – детерміновані коефіцієнти.

73. МОДЕЛЮВАННЯ СТАЦІОНАРНИХ ВИПАДКОВИХ ФУНКЦІЙ (2)

Обчислення коефіцієнтів:
K (t i t1 )
Приклад:
K t1 t1
2
K t 2 t1
2
K t 3 t1
2
2
n i 1
c j ci j 1 ;
i 1, n .
j 1
c 2j 2 c12 c22 c32 ;
3
j 1
2
2
c1c2 c2 c3 ;
c
c
j j 1
j 1
1
2
c1c3 .
c
c
j j 2
j 1

74. 3. ТЕХНОЛОГІЯ ІМІТАЦІЙНОГО МОДЕЛЮВАННЯ

ЕТАПИ ІМІТАЦІЙНОГО МОДЕЛЮВАННЯ
• побудова математичної моделі процесу
функціонування об'єкту;
• комп’ютерна реалізація моделюючого
алгоритму;
• статистична обробка результатів
моделювання.

75. ПОБУДОВА МАТЕМАТИЧНОЇ МОДЕЛІ

• постановка задачі моделювання;
• вибір незалежних і залежних змінних, характеристик станів і
шуканих характеристик процесу функціонування системи;
• підбір необхідної інформації про систему і зовнішнє
середовище, визначення параметрів системи і обурюючих дій,
оцінка їх впливу на процес функціонування системи;
• висунення гіпотез про властивості і характеристики системи;
прийняття припущень, що дозволяють спростити математичну
модель відповідно до вибраного рівня моделювання;
апроксимація реальних процесів, що протікають в модельованій
системі;
• формалізація функціональних залежностей між змінними,
параметрами і характеристиками станів системи; виведення
співвідношень для шуканих характеристик модельованого
процесу як функцій характеристик станів, змінних і параметрів
системи.

76. КОМП’ЮТЕРНА РЕАЛІЗАЦІЯ МОДЕЛЮЮЧОГО АЛГОРИТМУ

• побудова логічної схеми моделюючого
алгоритму;
• програмування моделюючого
алгоритму;
• визначення необхідної кількості
реалізацій моделюючого алгоритму, що
забезпечують необхідну точність і
достовірність результатів моделювання;
• проведення робочих розрахунків.

77. ПРИНЦИПИ ПОБУДОВИ МОДЕЛЮЮЧИХ АЛГОРИТМІВ

• принцип t ;
• принцип особливих станів (принцип z ).

78.

ПРИНЦИП t
Процес
z(t ) ( z1 (t ), z2 (t ), ..., zn (t )) ; t T .
Алгоритм
1. Визначення початкового стану:
z0 ( z01 , z02 ,..., z0 n ) ; z0 j z j (t 0 ); j 1, n .
2. Приріст аргументу часу:
tk tk 1 t t0 k t ; k 1, 2, 3, ...
3. Визначення характеристик наступного стану:
z j (tk 1 ) z j (tk 1 t ) z j (tk ) ; j 1, n .

79.

ПРИНЦИП z
Алгоритм
1. Визначення початкового стану:
z0 ( z01 , z02 ,..., z0 n ) ; z0 j z j (t 0 ); j 1, n .
2. Визначення часу настання чергового особливого
стану t k .
3. Визначення характеристик наступного (особливого)
стану:
z j (tk 1 ) z j (tk ) ; j 1, n .

80. 5. ОБРОБКА РЕЗУЛЬТАТІВ ЕКСПЕРИМЕНТУ

Оцінка вірогідності випадкової події
m
p ,
N
N – кількість експериментів;
m – кількість випадків настання випадкової події.
Оцінка вірогідності можливих значень випадкової
величини (закону її розподілу)
mk
; k 1, n .
pk
N
mk – кількість попадань значень випадкової величини в
k -й інтервал.

81. Оцінка середнього значення випадкової величини

1 N
x xi
N i 1
xi – значення випадкової величини , яке вона
прийняла в i -му експерименті.
Оцінка дисперсії випадкової величини
D( ) M [ M ( )]2
N
1
2
D
(
x
x
)
i
N 1 i 1
2
N
N
1
1
2
x
D
x
i
i
N 1 i 1
N ( N 1) i 1

82. Оцінка кореляційного моменту двох випадкових величин

K
K
1
N 1
1
N 1
N
N
( xi x )( yi y )
i 1
1
xi yi N ( N 1)
i 1
N
N
i 1
i 1
xi yi
x і y – середні значення випадкових величин і
відповідно.

83. Оцінка математичного очікування випадкового процесу

1 N
Z (t k )
Z i (t k ) ; k 1, r
N i 1
t k – фіксований момент часу; t k k t , k 1, r ;
випадкового процесу у i -й його
Z i (t k ) – значення
реалізації для t k -го моменту часу; i 1, N .
Оцінка кореляційної функції випадкового процесу
N
1
[ Z i (t ) Z (t )][ Z i (t ) Z (t )]
K (t , t )
N 1 i 1
N
1
1
Z i (t ) Z i (t )
K (t , t )
N ( N 1)
N 1 i 1
t , t {t k , k 1, r } .
N
N
i 1
i 1
Z i (t ) Z i (t ) ;

84. Оцінка математичного очікування стаціонарного випадкового процесу, що має ергодичну властивість

1T
Z lim
Z (t ) dt .
T0
T
t r
Z Z (t k )
T k 1

85. Оцінка кореляційної функції стаціонарного випадкового процесу, що має ергодичну властивість

1
K ( ) lim
T
T
T
2
Z
(
t
)
Z
(
t
)
dt
Z
,
0
де t t ; t , t (0, T ) .
де l
t
t
K ( )
T
r l
2
Z
(
t
)
Z
(
t
)
Z
,
k
k
k 1

86. Перевірка статистичних гіпотез

m
2
( N j N *j ) 2
N *j
– кількість рівних напіввідкритих
m
діапазону
спостережуваних
значень
величини ;
N j – емпірична частота; j 1, m ;
j 1
N *j – теоретична частота; j 1, m ;
Кількість ступенів свободи:
k m r 1.
Рівень значущості:
2
P[ 2 кр
( , k ) ]
Гіпотеза приймається, якщо
2
2 кр
( , k ) ,
2
( , k ) – критична точка.
де кр
інтервалів
випадкової

87. Точність і достовірність результатів імітаційного моделювання

Точність:
a x ,
де a – істинне значення параметру x .
Достовірність:
P( a x ) .
t D(x )

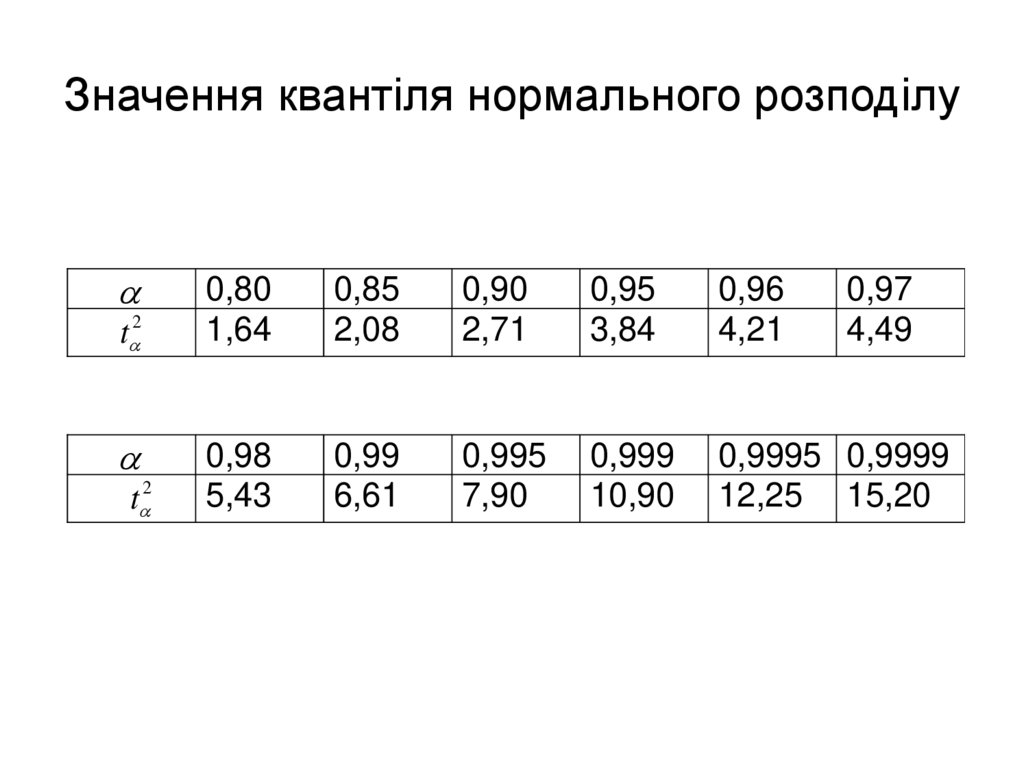
88. Квантіль нормального розподілу

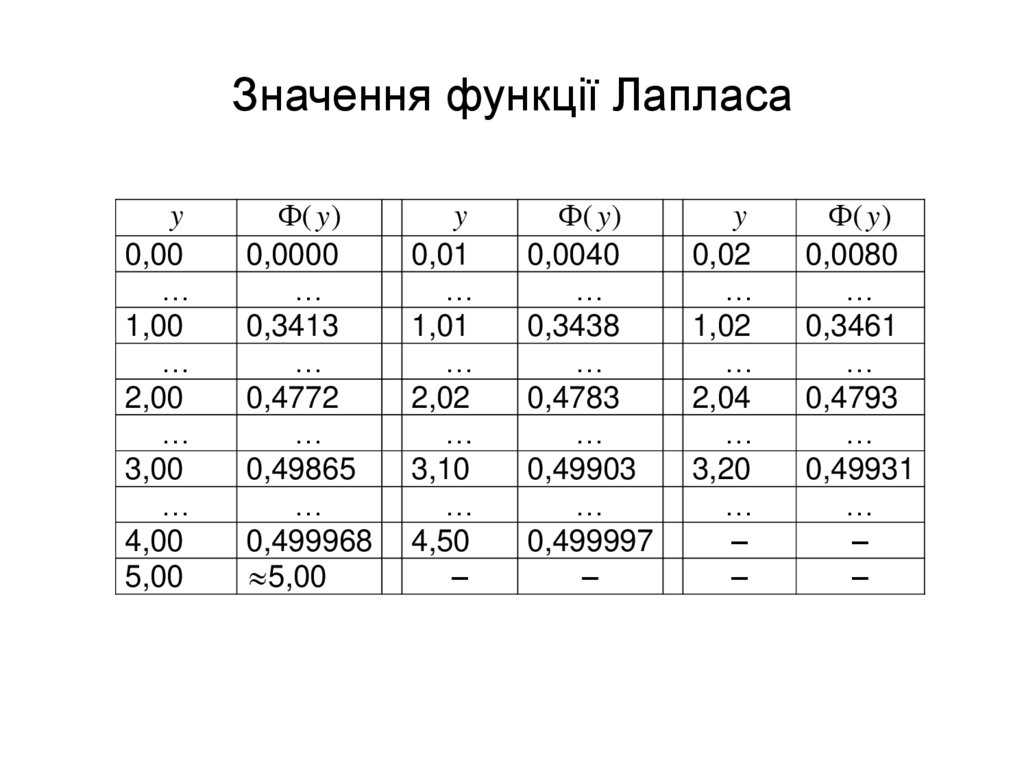
– значення аргумента, при якому функція Лапласа
приймає значення :
2
1
Функція Лапласа:
t ( )
2
( y )
y
1
e
2 0
(t )
2
.
z2
2
dz

89. Значення функції Лапласа

y
0,00
…
1,00
…
2,00
…
3,00
…
4,00
5,00
( y)
0,0000
…
0,3413
…
0,4772
…
0,49865
…
0,499968
5,00
y
0,01
…
1,01
…
2,02
…
3,10
…
4,50
–
( y)
0,0040
…
0,3438
…
0,4783
…
0,49903
…
0,499997
–
y
0,02
…
1,02
…
2,04
…
3,20
…
–
–
( y)
0,0080
…
0,3461
…
0,4793
…
0,49931
…
–
–

90. Значення квантіля нормального розподілу

t 2
t 2
0,80
1,64
0,85
2,08
0,90
2,71
0,95
3,84
0,96
4,21
0,97
4,49
0,98
5,43
0,99
6,61
0,995
7,90
0,999
10,90
0,9995 0,9999
12,25 15,20

91. Розрахунок кількості експериментів при визначенні ймовірності випадкової події

Кількість випадків настання події A у окремому
експерименті – випадкова величина , що набуває
значення:
z1 1 з вірогідністю p ;
z2 0 з вірогідністю (1 p) .
Математичне очікування і дисперсія випадкової
величини:
M ( ) z1 p z2 (1 p) p ;
D( ) [ z1 M ( ) ]2 p [ z 2 M ( ) ]2 (1 p) p(1 p) .

92. ОЦІНКА ВІРОГІДНОСТІ

m
p
N
N
m i
i 1
де i – кількість випадків настання події A у i -му
експерименті; i {0, 1}.
m 1
N N
N
i
i 1

93. ОЦІНКА ДИСПЕРСІЇ

N
m
1
1
M ( ) M ( i ) N M ( ) M ( ) p .
N
N
N
i 1
Друга властивість дисперсії:
D( K X ) K 2 D( X )
N
m
1 N
1
1
p(1 p)
D( ) D( i ) 2 D( i ) 2 N D( )
N
N i 1
N
N
N
i 1

94. НЕОБХІДНА КІЛЬКІСТЬ ЕКСПЕРИМЕНТІВ

p(1 p)
N
t
N t
2
p(1 p)
2
На початковому етапі:
m0
, 50 N 0 100
p0
N0

95. Приклад розрахунку кількості експериментів при визначенні ймовірності випадкової події

0,01; 0,95 ; p0 0,2 ;
t 2 3,84 ;
p 0 (1 p 0 )
0,2 0,8
N t
3,84
6140 .
2
0,0001
2

96. КІЛЬКІСТЬ ЕКСПЕРИМЕНТІВ ПРИ ВІДНОСНІЙ ТОЧНОСТІ

p
2
t
p
(
1
p
)
1
p
2
N t 2
t
p 2 2
p 2
p 2
Рекомендовано:
( p 10 k ) ( N 10 k 1 )

97.

Розрахунок кількості експериментів при визначенні
середнього значення випадкової величини з
математичним очікуванням a і дисперсією 2
Оцінка математичного очікування:
1 N
x xi .
N i 1
За центральною граничною теоремою:
1
M ( x ) N M ( ) a ;
N
(x)
1
N
N ( ) ;
1
D( ) 2
D( x ) ( x ) 2 N D( )
N
N
N
2

98. НЕОБХІДНА КІЛЬКІСТЬ ЕКСПЕРИМЕНТІВ

Точність оцінки x математичного очікування a :
t
2
t
N
Кількість експериментів:
2
N t 2 .
2
N
.

99. Приклад розрахунку кількості експериментів при визначенні середнього значення випадкової величини

0,01; 0,99 ; 0 0,2 ;
t 2 6,61 ;
0,04
N t 2 6,61
2644 .
0,0001
2
2
0