Вписанные в треугольник окружности. Решение задач

1. Решение задач

Вписанные в треугольник
окружности

2. Вписанные в треугольник окружности

› Вписанная в равнобедренный треугольник
окружность

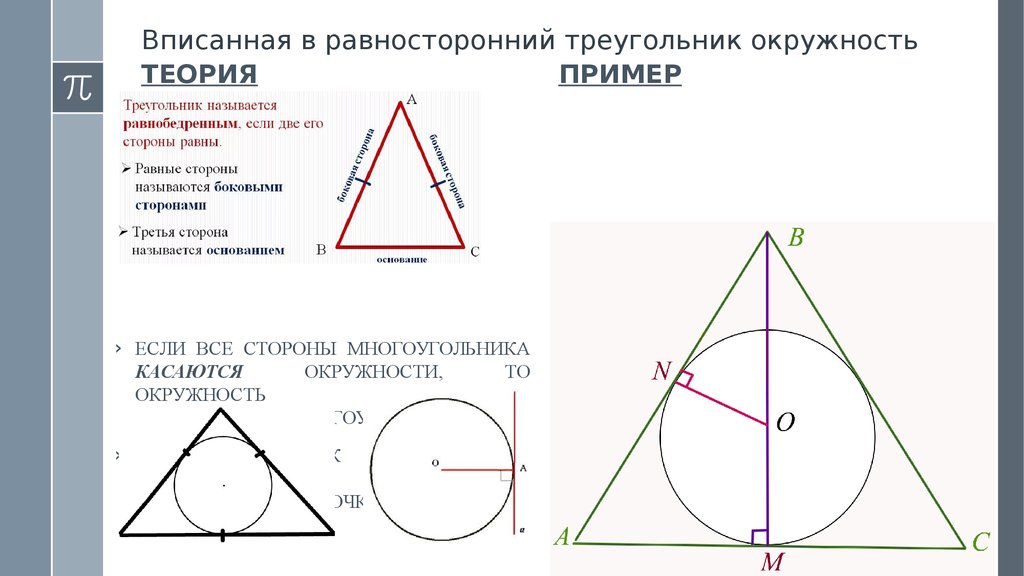
3. Вписанная в равносторонний треугольник окружность

ТЕОРИЯ
ПРИМЕР
НАЙДИТЕ РАДИУС ОКРУЖНОСТИ,
ВПИСАННОЙ В ТРЕУГОЛЬНИК СО
СТОРОНАМИ 10 СМ, 10 СМ, 12 СМ.
› ЕСЛИ ВСЕ СТОРОНЫ МНОГОУГОЛЬНИКА
КАСАЮТСЯ
ОКРУЖНОСТИ,
ТО
ОКРУЖНОСТЬ
НАЗЫВАЕТСЯ
ВПИСАННОЙ В МНОГОУГОЛЬНИК
› КАСАТЕЛЬНАЯ
К
ОКРУЖНОСТИ
ПЕРПЕНДИКУЛЯРНА
РАДИУСУ,
ПРОВЕДЕННОМУ В ТОЧКУ КАСАНИЯ
› AВ = BC = 10, AC = 12. ON - ?

4. Вписанная в равносторонний треугольник окружность

ТЕОРИЯ
ПРИМЕР
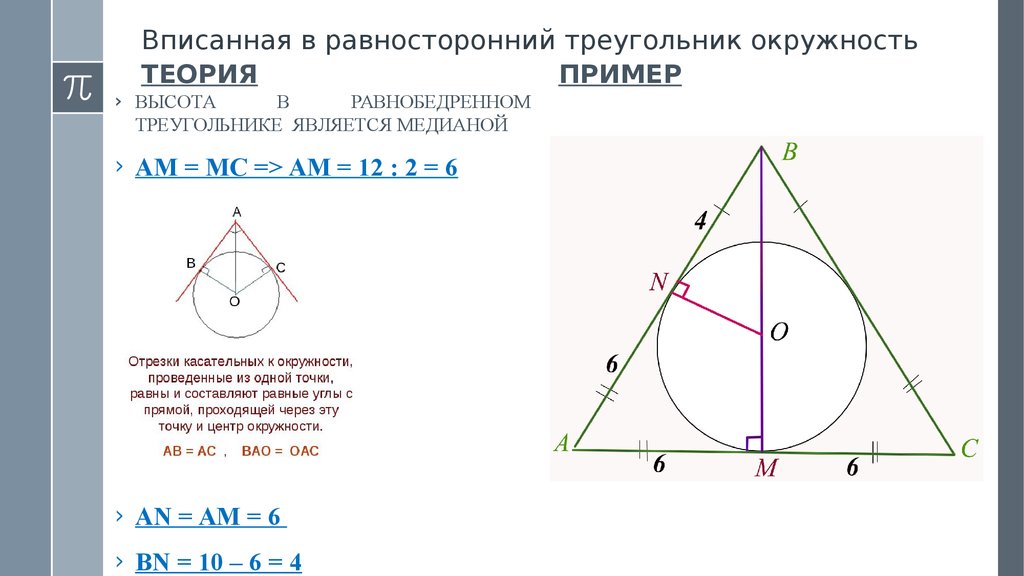
› ВЫСОТА
В
РАВНОБЕДРЕННОМ
ТРЕУГОЛЬНИКЕ ЯВЛЯЕТСЯ МЕДИАНОЙ
› AM = MC => AM = 12 : 2 = 6
› AВ = BC = 10, AC = 12. ON - ?
› AN = AM = 6
› BN = 10 – 6 = 4

5. Вписанная в равносторонний треугольник окружность

ТЕОРИЯ И РЕШЕНИЕ
ПРИМЕР
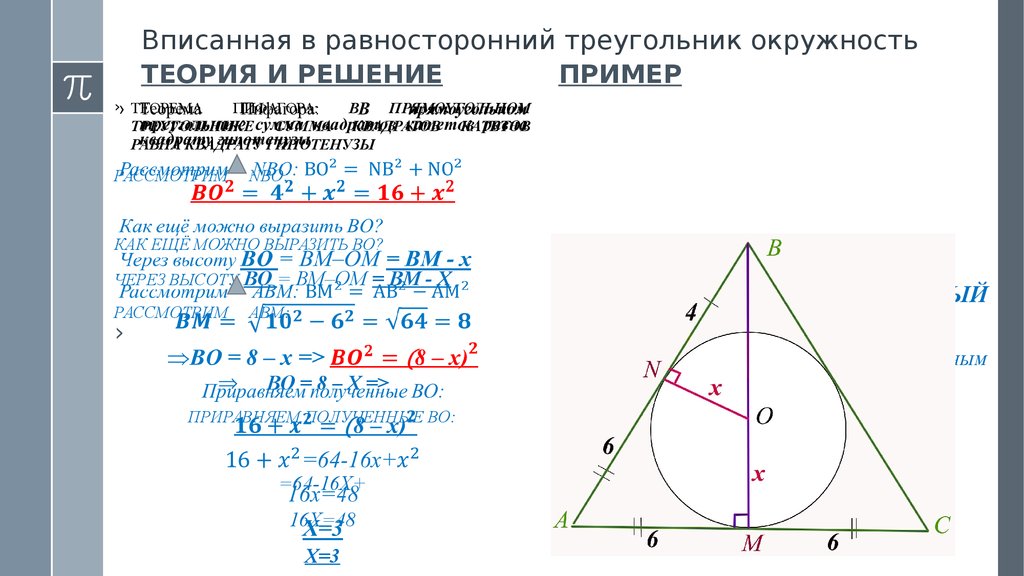
› ТЕОРЕМА
ПИФАГОРА:
В
ПРЯМОУГОЛЬНОМ
ТРЕУГОЛЬНИКЕ СУММА КВАДРАТОВ КАТЕТОВ
РАВНА КВАДРАТУ ГИПОТЕНУЗЫ
РАССМОТРИМ
NBO:
КАК ЕЩЁ МОЖНО ВЫРАЗИТЬ BO?
ЧЕРЕЗ ВЫСОТУ BO
РАССМОТРИМ
›  
= BM–OM = BM - X
АBМ:
BO = 8 – X =>
ПРИРАВНЯЕМ ПОЛУЧЕННЫЕ BO:
=64-16X+
16X=48
X=3
› AВ = BC = 10, AC = 12. ON - ?
› ОБОЗНАЧИМ ЧЕРЕЗ X ИСКОМЫЙ
РАДИУС (ON=OM=X)
(В СЛУЧАЕ ПОИСКА СТОРОНЫ
РАДИУСОМ ЧЕРЕЗ X ОБОЗНАЧИМ NB)
С
ИЗВЕСТНЫМ