Функционально замкнутые классы. Специальные классы булевых функций

1. Функционально замкнутые классы

2. Специальные классы булевых функций

Американский математик Эмиль Пост ввел в
рассмотрение следующие замкнутые классы булевых
функций:
• Функции, сохраняющие константу ноль T0 ;
• Функции, сохраняющие константу один T1;
• Самодвойственные функции S ;
• Монотонные функции M ;
• Линейные функции L .

3. Класс функций, сохраняющих константу 0

Определение. Говорят, что функция сохраняет константу
0, если f(0,0,…,0)=0
Примеры:
f(x,y)=x⊕y
f(x,y)=x·y
А
В А B
0
0
0
0
1
1
1
0
1
1
1
0

4. Класс функций, сохраняющих константу 1

Определение. Говорят, что функция сохраняет
константу 1, если f(1,1,…,1)=1
Примеры:
f(x,y)=x~y
f(x,y)=x·y
А
В
А B
0
0
0
0
1
0
1
0
0
1
1
1

5. Двойственность

Пусть f(x1, x2, …, xn ) – булева функция. Двойственной к ней
называется функция f*, которая на противоположных
наборах имеет значения, противоположные значениям
функции f.
ПРИМЕР
(x~y)*=x⊕y
А
В А B
(x·y)*=x+y
0
0
0
0
0
0
1
1
0
1
1
0
1
1
0
1
1
0
1
1

6. Класс самодвойственных булевых функций

Определение. Булева функция f(x1,…,xn) самодвойственна
(принадлежит классу S), если она равна двойственной себе,
то есть f(x1, …, xn) = f*(x1, …, xn)
Пример: f(x,y,z)=xy+yz+xz
Число различных самодвойственных булевых функций,
зависящих от n переменных, равно 22n –1.

7. Пример самодвойственной функции

• f(x,y,z)=xy+yz+xz
x
y
z
xy+yz+xz
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1

8. Алгоритм распознавания самодвойственной функции, заданной таблицей истинности 

Алгоритм распознавания
самодвойственной функции, заданной
таблицей истинности
• для проверки самодвойственности булевой
функции можно не получать двойственную ей
функцию в явном виде, а лишь сравнивать
значения исходной функции на
противоположных наборах.
• Функция самодвойственна, если и только если
на противоположных наборах принимает
противоположые значения.
Достаточное условие несамодвойственности булевой функции. Если число
единиц в столбце значений функции не совпадает с числом нулей, то
функция не является самодвойственной.

9.

Задача:
Являются ли функции f(x,y,z), g(x,y,z), h(x,y,z) самодвойственными?

10. Сравнимые наборы

Два набора ( 1, 2 ,..., n ) и ( 1, 2 ,..., n ) называются сравнимыми
( ), если i i , i 1, n
Запись означает, что набор предшествует набору .
Например, (0,0,1) (0,1,1). А наборы (0,1,0) и (1,0,0)
несравнимы

11. Класс монотонных функций

• Определение.
Булева
функция
f(x1,
…,
xn)
называется монотонной (принадлежит классу M), если
для любой пары наборов α и β таких, что α β, выполняется
условие монотонности: f(α)≤ f(β)
Пример: f(x,y)=x·y
f(x,y)=x+y
А В А B
А
В А+B
А В А→B
0
0
0
0
0
0
0
0
1
0
1
0
0
1
1
0
1
1
1
0
0
1
0
1
1
0
0
1
1
1
1
1
1
1
1
1

12.

Является ли функция монотонной?
Из элементарных булевых функций монотонными являются, например,
конъюнкция и дизъюнкция.
Не являются монотонными, например, штрих Шеффера и стрелка Пирса.
Теорема Булева функция, имеющая дизъюнктивную нормальную
форму, не содержащую отрицаний, является монотонной функцией,
отличной от 0 и 1.

13. Класс линейных функций

Определение. Булева функция
называется линейной (принадлежит классу L), если ее
полином Жегалкина линеен.
Из всех 16 булевых функций двух аргументов f(x1, x2) только 8 функций
(22+1) принадлежат классу L: 0, 1, , , тождественные функции x1 и
x2 и их инверсии x 1 и x 2
x+y=x⊕y⊕xy
x∼y=1⊕x⊕y
x→y=1⊕x⊕xy
x↓y=1⊕x⊕y⊕xy
x|y=1⊕xy

14.

Функциональная полнота
системы булевых функций

15. Функциональная полнота системы булевых функций

Определение ФПС
Определение. Множество функций N
называется функционально полной системой (ФПС), если
любая булева функция представима суперпозицией
функций из N
Определение . Система булевых функций {f1 f2, …, fn}
называется функционально полной, если произвольная булева
функция может быть выражена через функции f1 f2, …, fn.

16. Определение ФПС

Примеры ФПС
• Пример 1. Множество N1={&,+,–} является функционально
полной системой, так как любую булеву функцию, кроме
константы 0, можно представить совершенной ДНФ, то есть
суперпозицией функций из N1 а константу 0 – формулой xx .
• Пример 2. Множество N2={&, ,1} является ФПС, так как
любую булеву функцию можно представить полиномом
Жегалкина, то есть суперпозицией функций из N2, а
константу 0 – формулой 1 1

17. Примеры ФПС

Теорема о двух функционально полных
системах
• Теорема. Если даны два множества N1 и N2 булевых
функций и известно, что N1 – функционально полная
система, а каждая функция из N1 представима
суперпозицией функций из N2, то N2тоже является
функционально полной системой.
Пусть система {f1 f2, …, fn} — полна и любая из функций
f1, f2, …, fn может быть выражена через функции g1 g2, …, gn.
Тогда система {g1 g2, …, gn} также полна.

18. Теорема о двух функционально полных системах

• Пример. N1={&,+,–}, N2={&, –}.
Как показано ранее, N1 – ФПС. Конъюнкция и инверсия
содержатся в N2, а дизъюнкция представима суперпозицией
функций из N2:
x+y = x+y = x·y , значит, N2 – ФПС.

19.

Задание: Докажите, что система функций { , v} является полной.
Доказательство:
Пусть
f1(x1) = x1 f2(x1, x2) = x1 + x2 f3(x1, x2) = x1 & x2
g1(x1) =x1 g2(x1, x2) = x1 + x2
Выразим f1, f2, f3 через g1, g2
f1(x1) = g1(x1)
f2(x1, x2) = g2(x1, x2)
Используем закон де Моргана
f3(x1, x2) = x1 & x2 = x1 + x2 = g1(g2(g1(x1), g1(x2)))
Любая (сколь угодно сложная) булева функция может
быть выражена через две функции { , v} или { , &}.

20.

Штрих Шеффера (И-НЕ) – x1 | x2
Существует функционально полная система,
состоящая из одной булевой функции.
x1
0
0
1
1
x2
0
1
0
1
x1 | x2
1
1
1
0
Функция штрих Шеффера является базисом.

21.

Доказательство
x1 | x2 = x1 v x2 или x1 | x2 = x1 & x2
Тогда
x1 = x1 & x1 = x1 | x1
x1 + x2 = x1 + x2 = x1&x2 = x1 | x2 = (x1 | x1) | (x2 | x2)
x1 & x2 = x1 & x2 = x1 | x2 = (x1 | x2) | (x1 | x2)
Таким образом, мы выразили через функцию штрих
Шеффера функции { , &, v}.
Следовательно, система, состоящая только из функции
штрих Шеффера, полна.

22. Доказательство

Стрелка Пирса (ИЛИ-НЕ) – x1 ↓ x2
x1
0
0
1
1
x2
0
1
0
1
x 1 ↓ x2
1
0
0
0
Функция стрелка Пирса является
полной.
x1 ↓ x2 = x1 & x2 или x1 ↓ x2 = x1 + x2
Тогда
x1 = x1 + x1 = x1 ↓ x1
x1 + x2 = x1 + x2 = x1 ↓ x2 = (x1 ↓ x2) ↓ (x1 ↓ x2)
x1 & x2 = x1 & x2 = x1 + x2 = (x1 ↓ x1) ↓ (x2 ↓ x2)

23. Стрелка Пирса (ИЛИ-НЕ) – x1 ↓ x2

Теорема Поста
Теорема (о полноте). Для того, чтобы система булевых
функций Д была полной, необходимо и достаточно, чтобы
она целиком не содержалась ни в одном из пяти замкнутых
классов T0, T1, S, M, L.
Для того чтобы система S булевых функций была функционально полной,
необходимо и достаточно, чтобы эта система содержала хотя бы одну булеву
функцию, не сохраняющую константу 1, хотя бы одну булеву функцию, не
сохраняющую константу 0, хотя бы одну несамодвойственную булеву функцию,
хотя бы одну нелинейную булеву функцию и хотя бы одну немонотонную булеву
функцию.

24. Теорема Поста

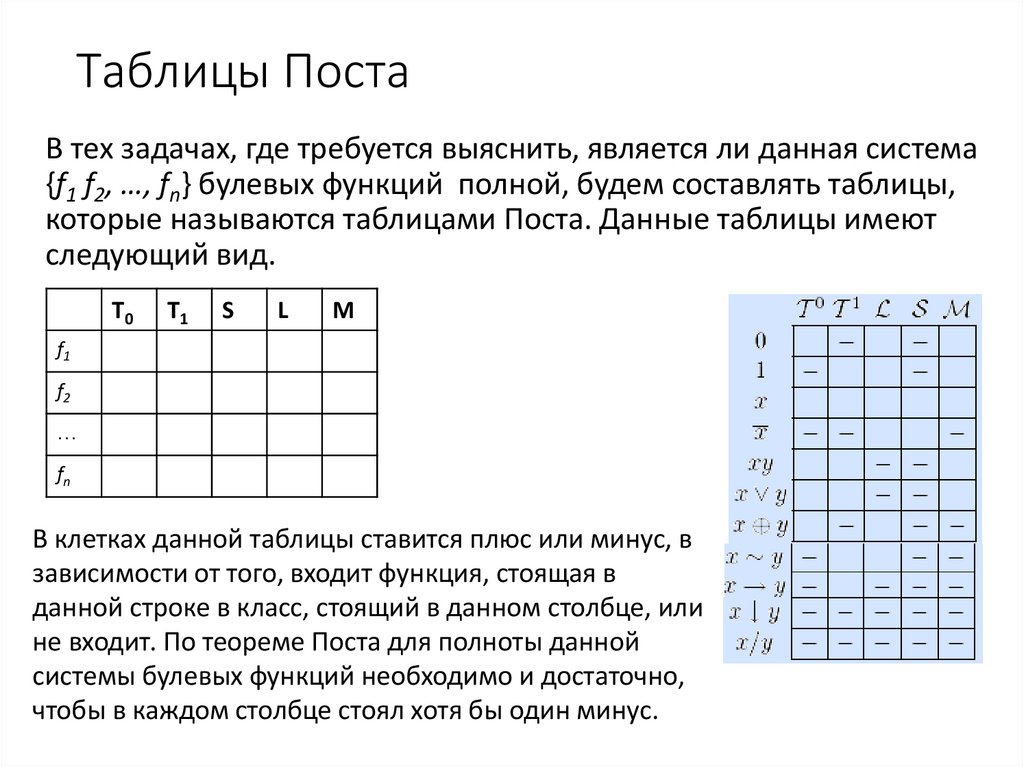
Таблицы Поста
В тех задачах, где требуется выяснить, является ли данная система
{f1 f2, …, fn} булевых функций полной, будем составлять таблицы,
которые называются таблицами Поста. Данные таблицы имеют
следующий вид.
T0
T1
S
L
M
f1
f2
fn
В клетках данной таблицы ставится плюс или минус, в
зависимости от того, входит функция, стоящая в
данной строке в класс, стоящий в данном столбце, или
не входит. По теореме Поста для полноты данной
системы булевых функций необходимо и достаточно,
чтобы в каждом столбце стоял хотя бы один минус.

25. Таблицы Поста

Пример. Выяснить, являются ли следующие системы булевых
функций полными. Являются ли следующие системы булевых
функций базисами.
D2={x y z, x&y, 0, 1}
F {x xy, x & y , x y}
F {x | y, y , y x}
F { x & y , x y x}

26.

Базис
Определение. Полная система функций называется базисом
пространства булевых функций, если любое собственное
подмножество данной системы функций уже не является
полным.
Другими словами, базис – это минимальная (но не по
количеству, а в смысле отношения включения) полная
система булевых функций.
Теорема. Всякий базис пространства булевых функций
содержит не более четырёх функций.