8 способов решения квадратного уравнения. 8 класс

1.

2.

«Для разыскания
истины вещей
необходим метод»
Рене Декарт
(французский математик)

3.

• Систематизировать знания,
умения, навыки решения
полных квадратных уравнений
различными способами.

4.

1.
2.
3.
4.
5.
6.
7.
8.
3x2-2x-5=0
X2=5
7x2+14x=0
X2+5x+4=0
X2+4x+4=0
X2-4=0
2x2-11x+5=0
X2+2x=x2+6
о
т
Д
ф
и
а
н

5. Диофант Александрийский (около 3 в.).

Древнегреческий
математик. В основном
труде «Арифметика»
(сохранились 6 книг из
13), дал решение задач,
приводящихся к
диофантовым
уравнениям, и впервые
ввел буквенную
символику в алгебру.

6.

Способы решения
квадратного уравнения
ax2+bx+c=0

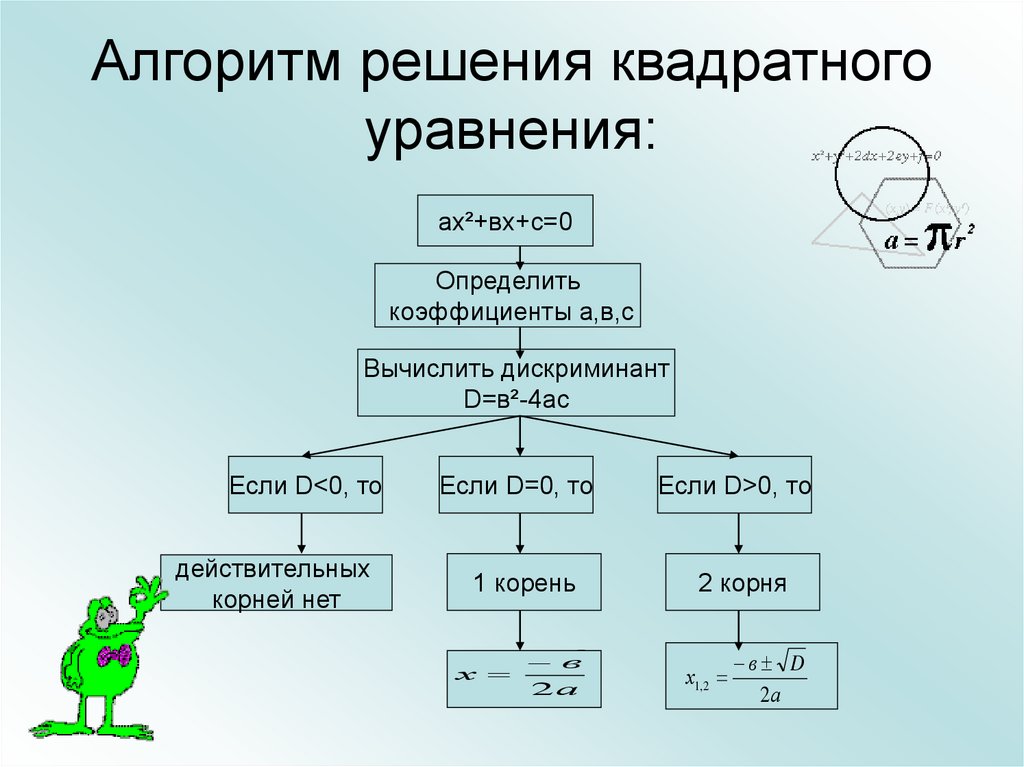
7. Алгоритм решения квадратного уравнения:

ах²+вх+с=0
Определить
коэффициенты а,в,с
Вычислить дискриминант
D=в²-4ас
Если D<0, то
действительных
корней нет
Если D=0, то
1 корень
х
х
в
2а
в
2а
Если D>0, то
2 корня
х1, 2
х1, 2
вв D
D
2а
2а

8.

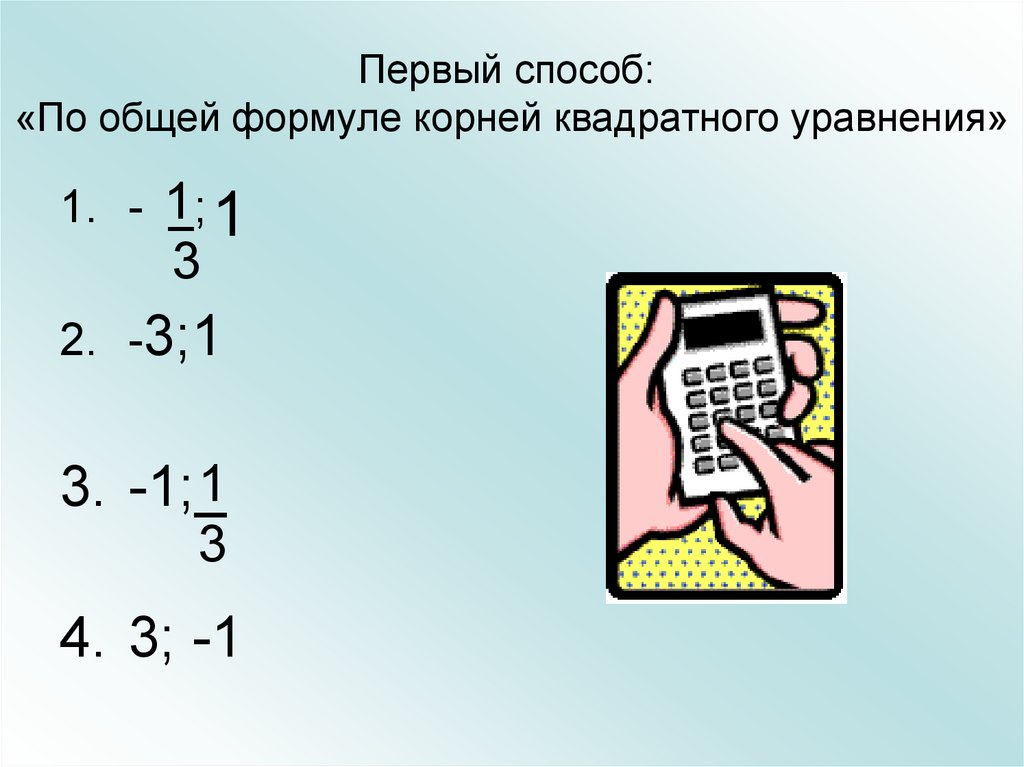
Первый способ:
«По общей формуле корней квадратного уравнения»
1. - 1
_; 1
3
2. -3;1
1
3. -1;_
3
4. 3; -1

9. Формула корней квадратного уравнения с четным вторым коэффициентом

ax 2 bx c 0
b 2k четное число
x
x1
x2
k
k 2 ac
a
1 1 3 ( 1) 1 4 1 2 1
3
3
3
3
1 1 3 ( 1) 1 4 1 2
3
1
3
3
3
3

10. Работа в группах.

11.

Предупредительный сигнал об
окончании работы
Осталось
15
секунд!

12. Способ №3

«Разложение левой части уравнения на
множители способом группировки».

13.

Приёмы устного решения
квадратных уравнений.
a x 2 + b x + c = 0.
с
1.Если a + b + c = 0, x1 = 1, x2 =
а
2.Если a - b + c = 0,
с
x 1= - 1, x2 =
а

14.

Голландский математик родился
в 1540 году. Получив юридическое
образование он занимался
адвокатской практикой. Главной
страстью Виета была математика.
Теорема ( обратная теореме Виета):
Если сумма двух чисел равна второму
коэффициенту приведённого
квадратного уравнения, взятому с
противоположным знаком, а их
произведение равно свободному
члену, то эти числа являются
корнями приведённого квадратного
уравнения.

15. Формулы сокращенного умножения

a2+2ab+b2=(a+b)2
a2-b2=(a-b)(a+b)

16. Разложение квадратного трехчлена на множители

Если квадратное уравнение
a x 2 + b x + c = 0 имеет корни x1; x2,
то выполняется тождество:
a x 2 + b x + c=a(x-x1)(x-x2).

17.

Способ №8: Графический
Y
3x2=-2x+1
Y=3x2
.А
y=3x2
3
Y=-2x+1
2
1
.В
X
-1
01
1
3
y=-2x+1