Дифференцированный подход при подготовке к итоговой аттестации в 9 классе

1.

Дифференцированный
подход при подготовке
к итоговой аттестации
в 9 классе

2.

ЦЕЛИ:
1. Организовать подготовку, соблюдая
подбор задач от простого к сложному
2. Достичь усвоения базового уровня
знаний
3. Успешная сдача экзамена

3.

СОДЕРЖАНИЕ:
1. Рациональные неравенства
2. Системы уравнений
3. Свойства функции
4. Степенные функции
5. Арифметическая и
геометрическая прогрессии

4.

РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
К каждому из заданий 1 – 4 даны 4 варианта ответа, из которых
только один правильный. Номер этого ответа обведите кружком
1. Какое из приведенных ниже неравенств является верным при любых
значениях a и b, удовлетворяющих условию a > b ?
А) b – a > 0.
Б) b – a < - 1.
В) a – b > 3.
Г) a – b > - 2.
2. Сколько решений неравенства
среди чисел – 2, 0, 1, 3 ?
А) 1.
Б) 2.
3х2 – 5х – 12 > 0
В) 3.
3. Решите неравенство -1/4 х + 12 < 0.
А) x < 3.
Б) x < -3.
В) x > - 48.
4. Решите неравенство х2 < 9.
А) x < 3.
Б) x < - 3.
В) – 3 < x < 3.
содержится
Г) 4.
Г) x > 48.
Г) x < - 3; x >

5.

РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
5. При выполнении задания в таблице под каждой буквой
укажите номер рисунка, на котором изображено
соответствующее множество решений системы
ответ
А
Б
В
6. При выполнении задания запишите ответ в отведенном для
него месте
Решите неравенство
2(1 – х) ≥ 5х – (3х + 2).
Ответ:____________

6.

РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Часть 2
В заданиях 7 – 9 проведите полное решение и запишите ответ
7. Найдите область определения выражения
8. Решите систему неравенств
9. При каких значениях параметра m уравнение 4х2 – 2mх + 9 =0 имеет
два корня?

7.

СИСТЕМЫ УРАВНЕНИЙ
Часть 1
К каждому из заданий 1 – 4 даны 4 варианта ответа, из которых
только один правильный. Номер этого ответа обведите кружком
1. Какая из следующих пар чисел является решением системы уравнений
2. Какая система уравнений имеет решением пару чисел (2;3)?
3. Из данных уравнений подберите второе уравнение системы
так, чтобы она имела два решения
4. Решите систему уравнений:

8.

СИСТЕМЫ УРАВНЕНИЙ
При выполнении заданий 5 и 6 запишите ответ в отведенном для
него месте
5
6

9.

СИСТЕМЫ УРАВНЕНИЙ
Часть 2
В заданиях 7 – 9 проведите полное решение и запишите ответ.
7
8
9

10.

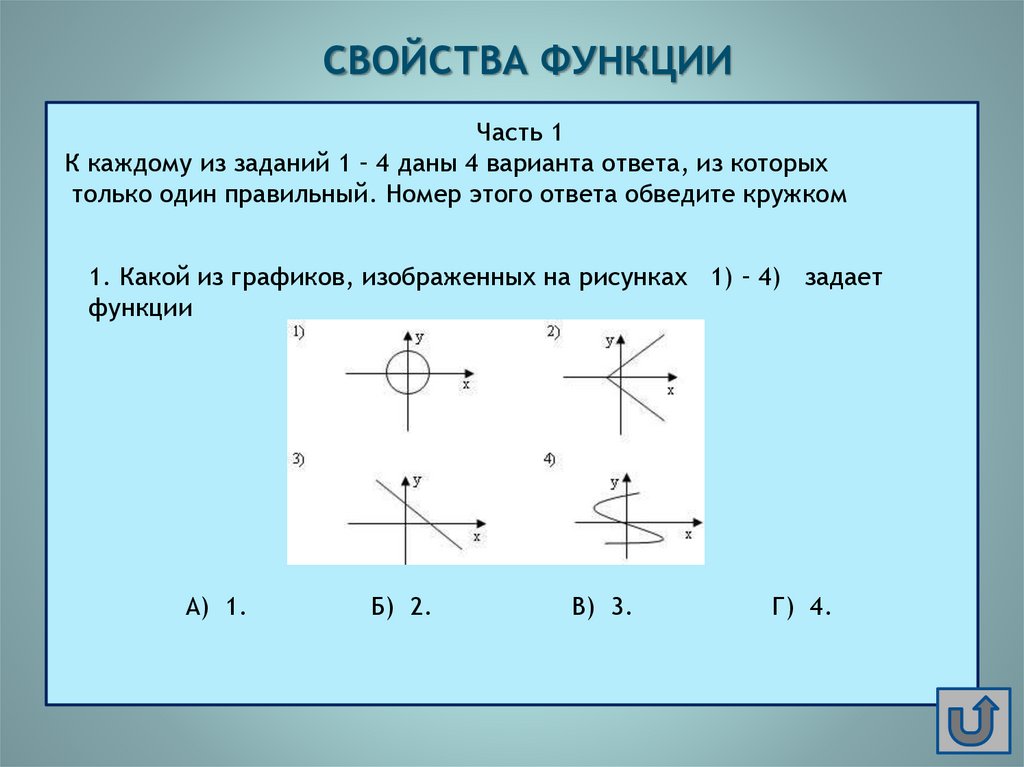
СВОЙСТВА ФУНКЦИИ
Часть 1
К каждому из заданий 1 – 4 даны 4 варианта ответа, из которых
только один правильный. Номер этого ответа обведите кружком
1. Какой из графиков, изображенных на рисунках 1) – 4) задает
функции
А) 1.
Б) 2.
В) 3.
Г) 4.

11.

СВОЙСТВА ФУНКЦИИ
2.Найдите область определения функции
А) x > 2.
Б) x < 2
В) x ≥ 1/2 .
Г) x ≤ 2.
3.Среди заданных функций укажите возрастающие.
1) у = 2х2.
2) у = 5х – 1.
3) у = 3 – х.
4) у = √x.
А) 2) и 4).
Б) 1), 2) и 4).
В) 3).
Г) 1) и 2).
4.Среди заданных функций укажите четные.
1) у = 2х2.
2) у = √x.
А) 1) и 3).
Б) 1) и 2).
3) у = 5х.
В) 3) и 4).
4) у = |x|.
Г) 1) и 4).

12.

СВОЙСТВА ФУНКЦИИ
При выполнении заданий 5 и 6 запишите ответ в отведенном для
него месте
5.Найдите область определения функции у = (2x+1)/(x(x+1)).
Ответ:_____________
6.Каждую прямую, построенную на координатной плоскости,
соотнесите с ее уравнением.
а) у = х;
б) х = 2;
в) у = 2;
г) у = -2.

13.

СВОЙСТВА ФУНКЦИИ
Часть 2
В заданиях 7 – 9 проведите полное решение и запишите ответ
7.Найдите область определения функции
8.Постройте график функции у = (6-x)/2. При каких, значениях х
функция принимает положительные значения?
9.Постройте график функции у = f(x), где
Найдите значение функции при х = -10.

14.

СТЕПЕННЫЕ ФУНКЦИИ
Часть 1
К каждому из заданий 1 – 4 даны 4 варианта ответа, из которых
только один правильный. Номер этого ответа обведите кружком
1.Среди заданных функций укажите четные:
1) у = х5;
2) у = х- 10;
3) у = х6;
4) у = х- 7.
А) 1) и 4).
Б) 2) и 3).
В) 1) и 3).
Г) 2) и 4).
2.Среди заданных функций укажите те, которые убывают при х > 0 :
1) у = х5;
2) у = х– 10;
3) у = х6;
4) у = х– 7.
А) 1) и 4).
Б) 2) и 3).
В) 1) и 3).
Г) 2) и 4).
3.Найдите наименьшее значение функции у = - х4 на отрезке [ -1; 2].
А) -16.
Б) -1.
В) 0.
Г) -8.
4.Сколько среди заданных функций тех, которые ограничены сверху
1) у = х5;
2) у = х– 10;
3) у = х– 4; 4) у = х– 7 ?
А) 3.
Б) 2.
В) 1.
Г) 0.

15.

СТЕПЕННЫЕ ФУНКЦИИ
При выполнении заданий 5 и 6 запишите ответ в отведенном для
него месте
5.Найдите наибольшее и наименьшее значения функции у = х6
на отрезке [- 1; 2].
Ответ:________
6.Сколько корней имеет уравнение -0,5х4 = х – 4 ?
Ответ:___________

16.

СТЕПЕННЫЕ ФУНКЦИИ
Часть 2
В заданиях 7 – 9 проведите полное решение и запишите ответ
7.Найдите наибольшее и наименьшее значения функции
у =(х – 2)3 + 4 на отрезке [ 0; 3]
8. Решите графически уравнение
9. Решите графически неравенство

17.

АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
Часть 1
В заданиях 1-4 даны 4 варианта ответов, из которых только один верный.
Обведите кружком номер правильного ответа
1.Найдите четвертый член арифметической прогрессии: 13; 9; …
А) 0.
Б) 6.
В) -1.
Г) 1.
2. Найдите первый член геометрической прогрессии: b1; b2; 4; - 8; …
А) 1.
Б) -1.
В) 28.
Г) 0,5.
3. Какое из чисел является членом арифметической прогрессии: 3; 6; 9;… ?
А) 83.
Б) 95.
В) 100.
Г) 102.
4. В геометрической прогрессии b1 = 81; q = -1/3. В каком случае при сравнении
членов этой прогрессии знак неравенства поставлен неверно?
А) b2 < b3.
Б) b3 > b4.
В) b4 > b6 .
Г) b5 > b7 .

18.

АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
В заданиях 5 и 6 запишите ответ в отведенном для этого месте
5. Для каждой арифметической прогрессии, заданной формулой n-го
члена, укажите ее разность d. (В таблице под каждой буквой запишите
номер ответа, под которым указана соответствующая разность).
А) а n = 3n + 1
1) d = - 7
ответ
Б) а n = 10n – 7
2) d = 10
3) d = 4
А
Б
В) а n = 4n + 3
4) d = 3
В
6. Найдите сумму первых шестнадцати членов арифметической
прогрессии, заданной формулой а n = 6n +2.
Ответ: _______________

19.

АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
Часть 2
В заданиях 7 – 9 проведите полное решение и запишите ответ.
7. Пятый член арифметической прогрессии равен 8, 4, а ее
десятый член равен 14,4. Найдите пятнадцатый член этой
прогрессии.
8. Найдите сумму всех последовательных натуральных чисел с 60
до 110 включительно.
9. Между числами 2 и 18 вставьте три числа так, чтобы
получилась геометрическая прогрессия.

20.

Удачи на экзаменах!
Урок составила: Смирнова Ирина Рудольфовна
МБОУ СОШ № 10
г. Апатиты Мурманской области