Похожие презентации:
Рентгеновские лучи
1.
Рентгеновские лучиОбразование рентгеновского излучения связано с
остановкой быстролетящих электронов.
тормозное излучение.
При не слишком больших энергиях бомбардирующих
антикатод электронов наблюдается лишь тормозное
рентгеновское излучение со сплошным спектром, не
зависящее от материала антикатода.
2.
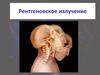
Рентгеновские лучиКоротковолновая граница тормозного рентгеновского
излучения рассчитывается просто:
h
U – ускоряющее напряжение,
hc
гр
eU
hc
гр
eU
Дифракция на кристаллах,
1912 г., Макс Лауэ, Электромагнитные
волны, измерение длины волны, сложный
спектр тормозного рентгеновского
излучения. Коротковолновая граница,
квантовая природа, измерение
ħ.
3.
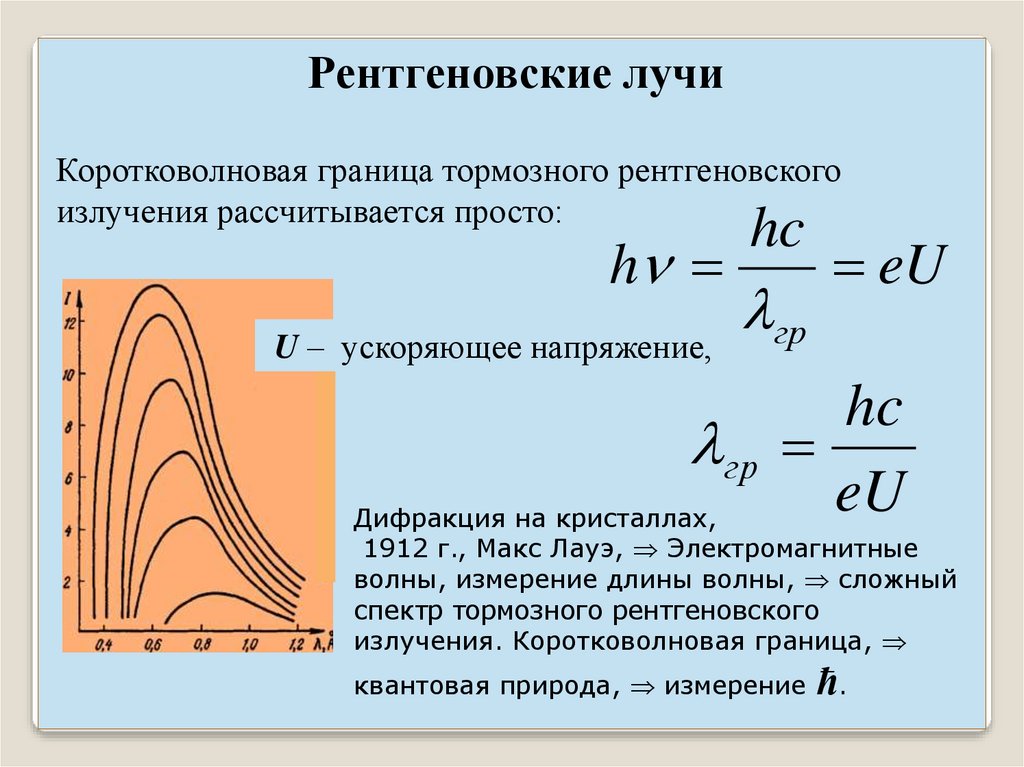
характеристическое излучениеПри увеличении энергии электронов, на фоне тормозного
излучения появляются резкие линии характеристического
излучения. Частоты этих линий зависят от материала
антикатода.
4.
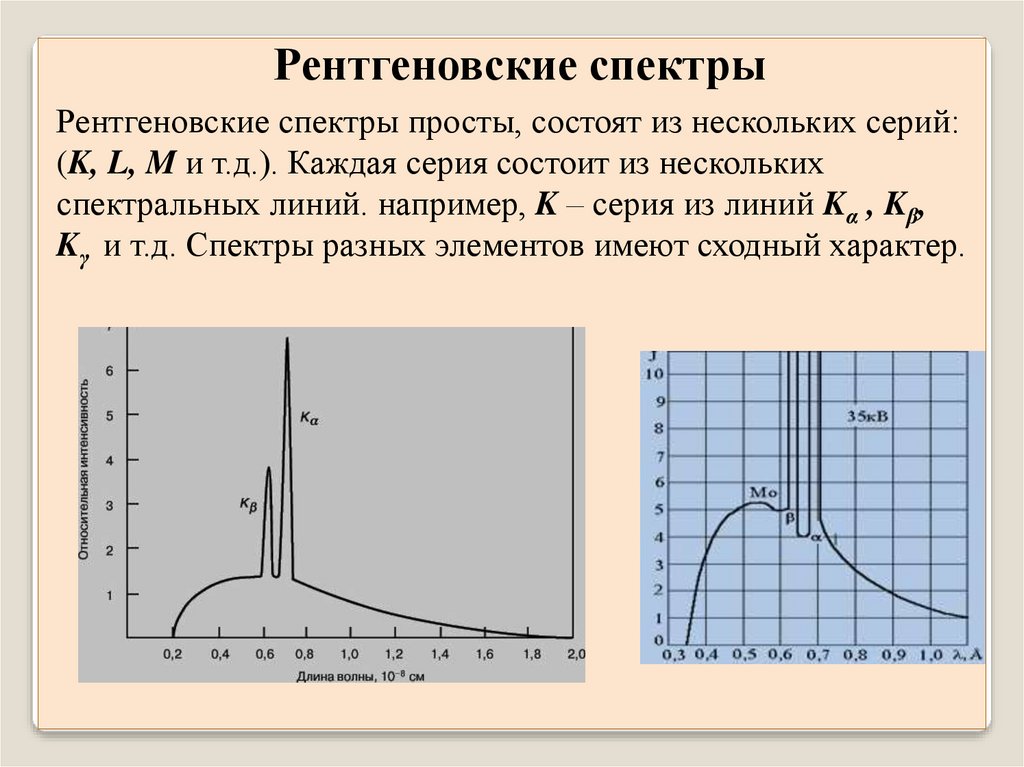
Рентгеновские спектрыРентгеновские спектры просты, состоят из нескольких серий:
(K, L, M и т.д.). Каждая серия состоит из нескольких
спектральных линий. например, K – серия из линий Kα , Kβ,
Kγ и т.д. Спектры разных элементов имеют сходный характер.
5.
Рентгеновские спектрыСпектры разных элементов
имеют сходный характер. При
увеличении атомного номера Z,
весь рентгеновский спектр
смещается в коротковолновую
область, не меняя структуры.
Объясняется это тем, что эти
спектры возникают при
переходах во внутренних слоях
атомов, которые имеют сходное
строение.
6.
Закон МозлиГенри Мозли в 1913 г. установил закон, связывающий частоты
линий рентгеновского спектра с атомным номером Z
элемента.
C Z
Где С и σ – постоянные.
Т.е. корень из частоты является
линейной функцией атомного
номера
Z элемента
7.
Закон МозлиЗакон Мозли позволяет
по измеренной длине
волны
характеристического
рентгеновского
излучения точно
установить атомный
номер Z элемента
большая роль в
размещении элементов в
периодической таблице.
8.
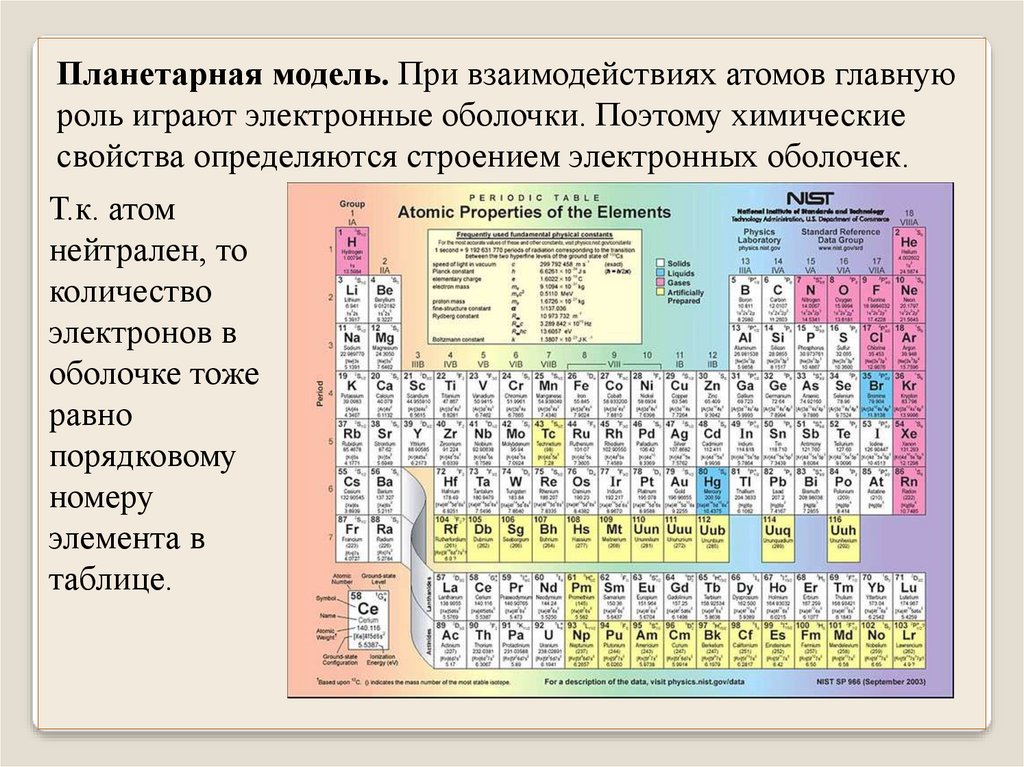
Планетарная модель. При взаимодействиях атомов главнуюроль играют электронные оболочки. Поэтому химические
свойства определяются строением электронных оболочек.
Т.к. атом
нейтрален, то
количество
электронов в
оболочке тоже
равно
порядковому
номеру
элемента в
таблице.
9.
характеристическое излучениеБлижайшая к ядру оболочка называется K – оболочкой,
следующая L – оболочкой, затем следует M – оболочка и т.д.
Внешние электроны связаны с атомами слабее внутренних т.к.
находятся на больших расстояниях и действие ядра для них
экранировано внутренними электронами невысокие
энергии для их возбуждения и отрыва ( 20 эВ) оптический
диапазон.
Гораздо большая энергия нужна для отделения внутренних
электронов и эта энергия растет с увеличением заряда ядра.
Например, чтобы вы рвать электрон с K – оболочки:
необходимы следующие значения энергии: натрий (Z = 11) –
1 кэВ, медь (Z = 29) – 9 кэВ, вольфрам (Z = 74) – 70 кэВ.
10.
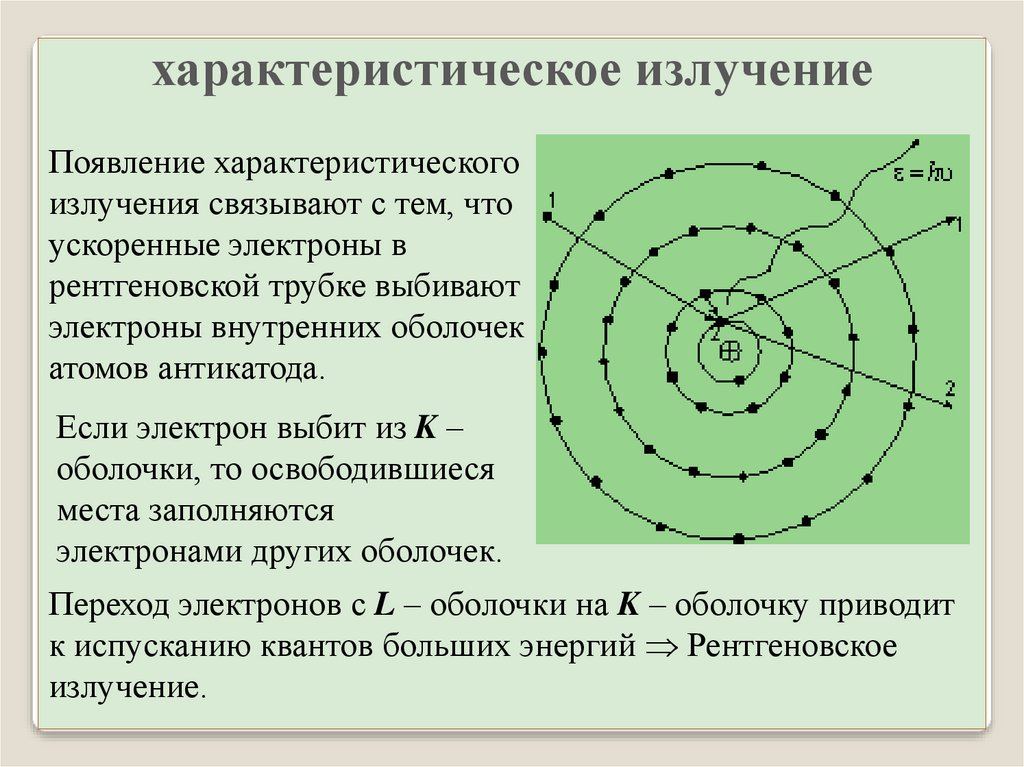
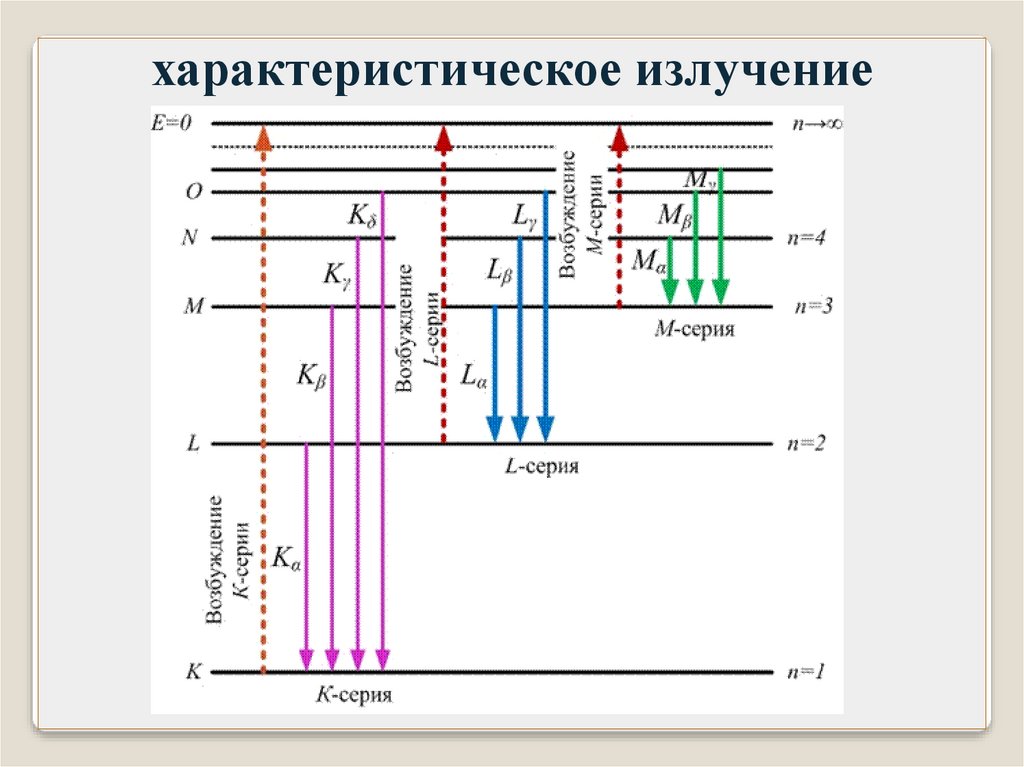
характеристическое излучениеПоявление характеристического
излучения связывают с тем, что
ускоренные электроны в
рентгеновской трубке выбивают
электроны внутренних оболочек
атомов антикатода.
Если электрон выбит из K –
оболочки, то освободившиеся
места заполняются
электронами других оболочек.
Переход электронов с L – оболочки на K – оболочку приводит
к испусканию квантов больших энергий Рентгеновское
излучение.
11.
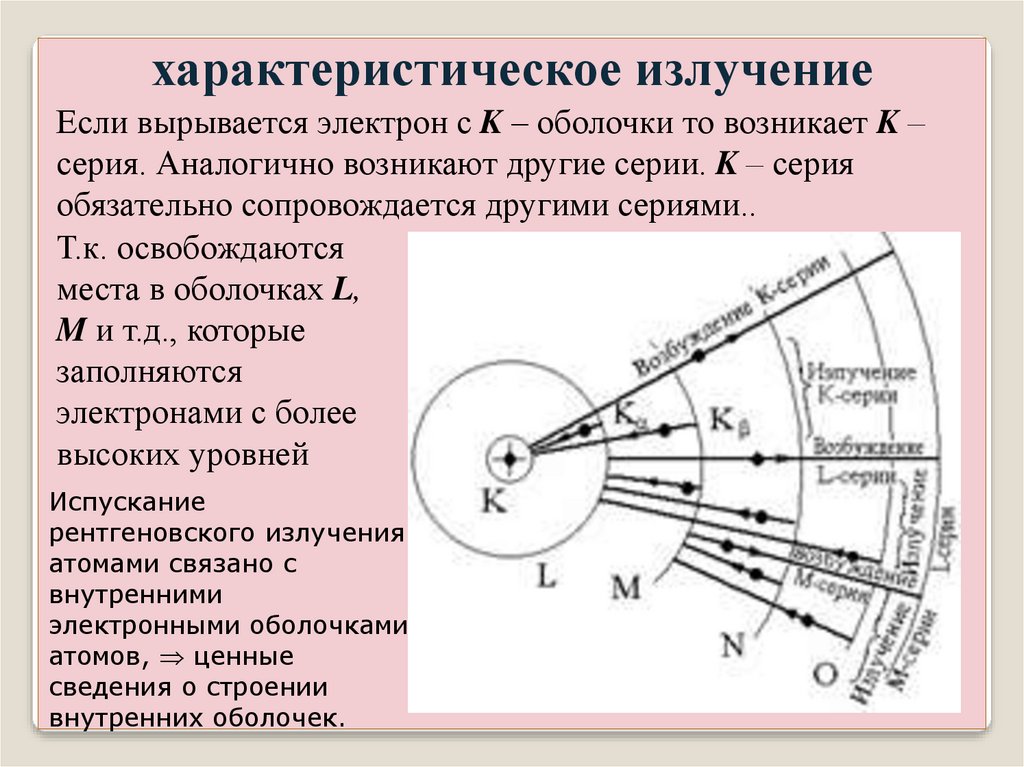
характеристическое излучениеЕсли вырывается электрон с K – оболочки то возникает K –
серия. Аналогично возникают другие серии. K – серия
обязательно сопровождается другими сериями..
Т.к. освобождаются
места в оболочках L,
M и т.д., которые
заполняются
электронами с более
высоких уровней
Испускание
рентгеновского излучения
атомами связано с
внутренними
электронными оболочками
атомов, ценные
сведения о строении
внутренних оболочек.
12.
характеристическое излучение13.
Закон МозлиПостоянная экранирования σ
учитывает экранирование
заряда ядра электронами
внешних оболочек. Для легких
атомов антикатода она равна 1
для K – серии и 7.5 для L –
серии.
Более строгая формула должна
выглядеть так:
Z 2 Z 2
R
2
n2
n
2
1
14.
Закон МозлиСогласно этому закону Мозли, длины волн K – серии
можно представить формулой:
R Z b
2
Здесь Z – заряд ядра атома антикатода,
R – постоянная Ридберга,
σ – постоянная экранирования,
для линии Kα
Для других линий величину b можно
рассчитать аналогичным образом,
для линии Kβ
и т д.
3 1 1
b 2 2
4 1 2
8 1 1
b 2 2
9 1 3
15.
первая модель атомаПо классическим представлениям, чтобы излучать
электромагнитную волну, электрон в атоме должен совершать
гармонические колебания,
2
x x 0
и удерживаться около положения равновесия квазиупругой
силой.
F = -kr
Где r – отклонение от положения равновесия.
e2
F e E 3 r
R
Колебания с частотой
e2
R3
16.
первая модель атомаВ 1903 году Дж. Томсон предложил модель атома. Равномерно
положительно заряженный шар внутри которого находится
электрон. Сумма зарядов равна нулю. Атом нейтрален.
Оценка размера атома по этой формуле:
R ≈ 3·10-10 м подтверждение.
В дальнейшем выяснилась
несостоятельность.
Исторический интерес.
17.
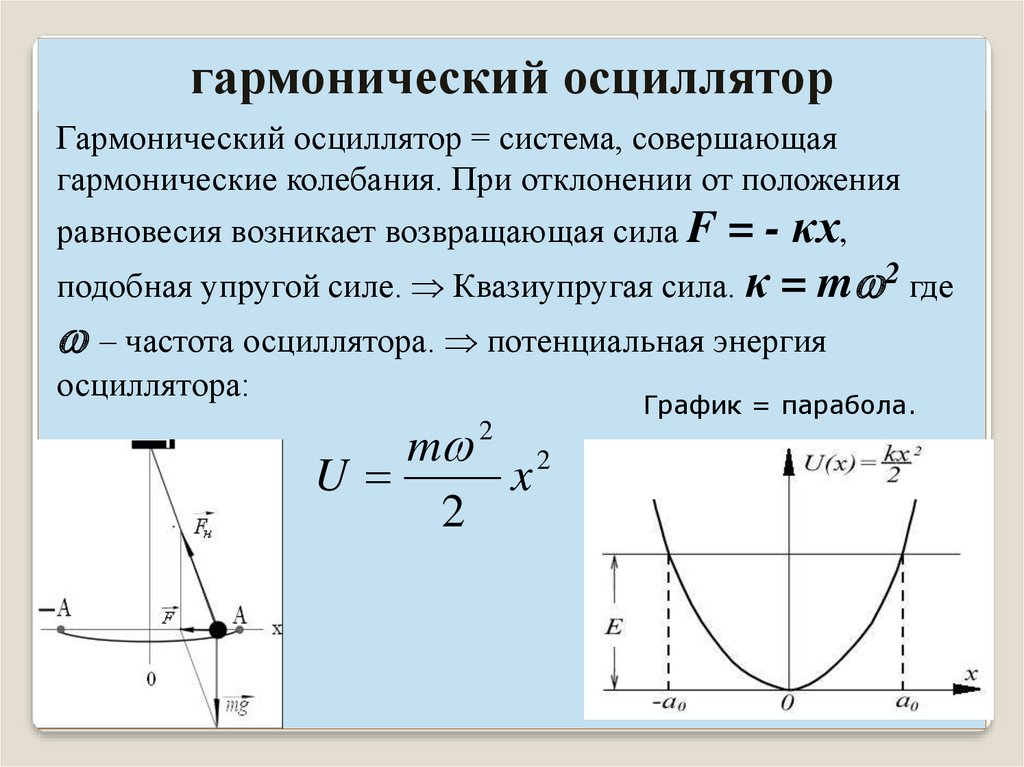
гармонический осцилляторГармонический осциллятор = система, совершающая
гармонические колебания. При отклонении от положения
= - κx,
подобная упругой силе. Квазиупругая сила. κ = m 2 где
равновесия возникает возвращающая сила F
– частота осциллятора. потенциальная энергия
осциллятора:
m 2 2
U
x
2
График = парабола.
18.
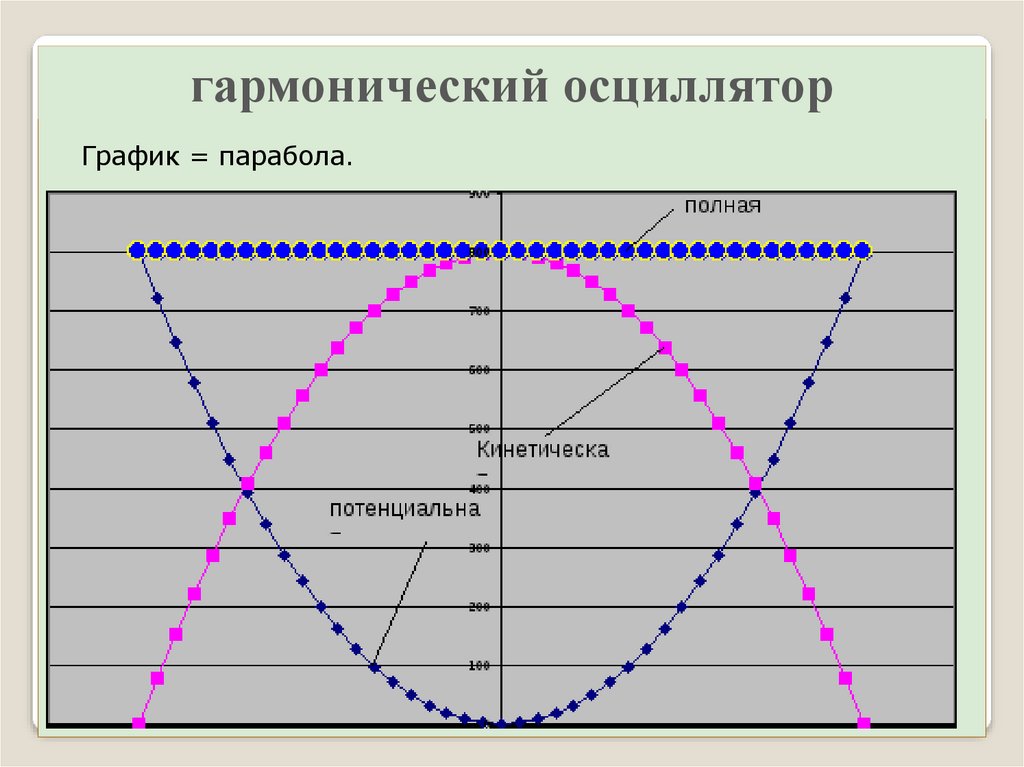
гармонический осцилляторГрафик = парабола.
19.
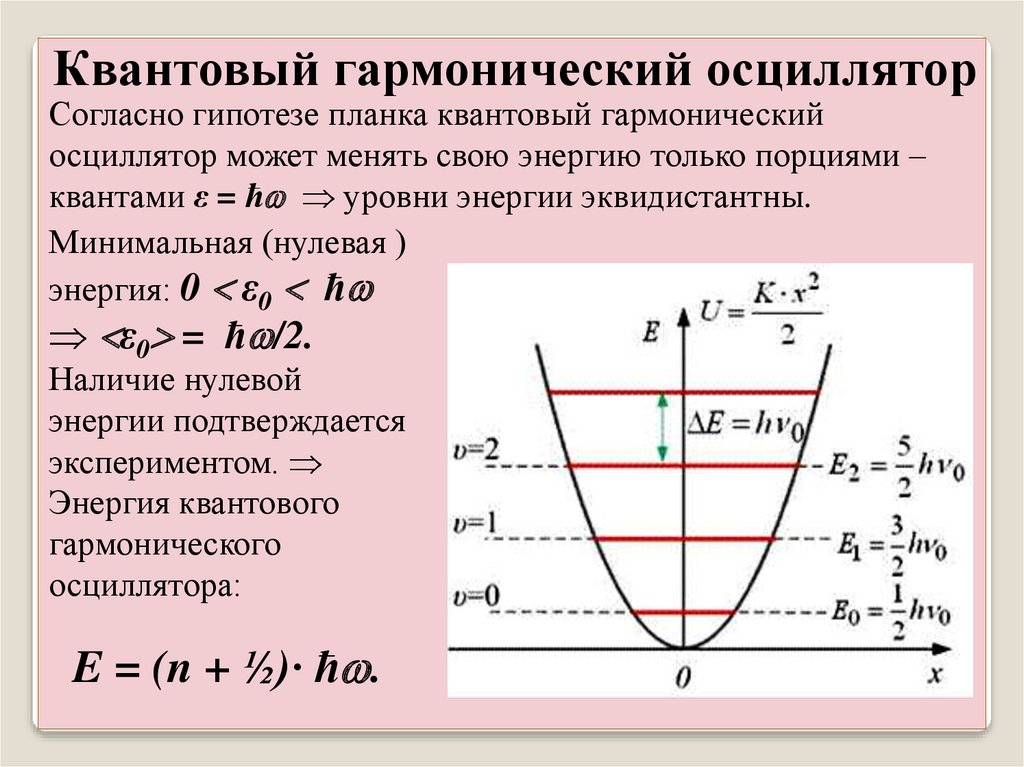
Квантовый гармонический осцилляторСогласно гипотезе планка квантовый гармонический
осциллятор может менять свою энергию только порциями –
квантами ε = ħ уровни энергии эквидистантны.
Минимальная (нулевая )
энергия: 0 ε0 ħ
ε0 = ħ /2.
Наличие нулевой
энергии подтверждается
экспериментом.
Энергия квантового
гармонического
осциллятора:
E = (n + ½)· ħ .
20.
Квантовый гармонический осцилляторДля квантового гармонического
осциллятора возможны переходы
лишь между соседними
стационарными уровнями:
n = 1 . При каждом переходе
испускается или поглощается
фотон с энергией ħ .
В колебательных макросистемах (маятниках) квантовые
эффекты не проявляются из-за малости ħ и (малые
порции).
Существование нулевой энергии.
21.
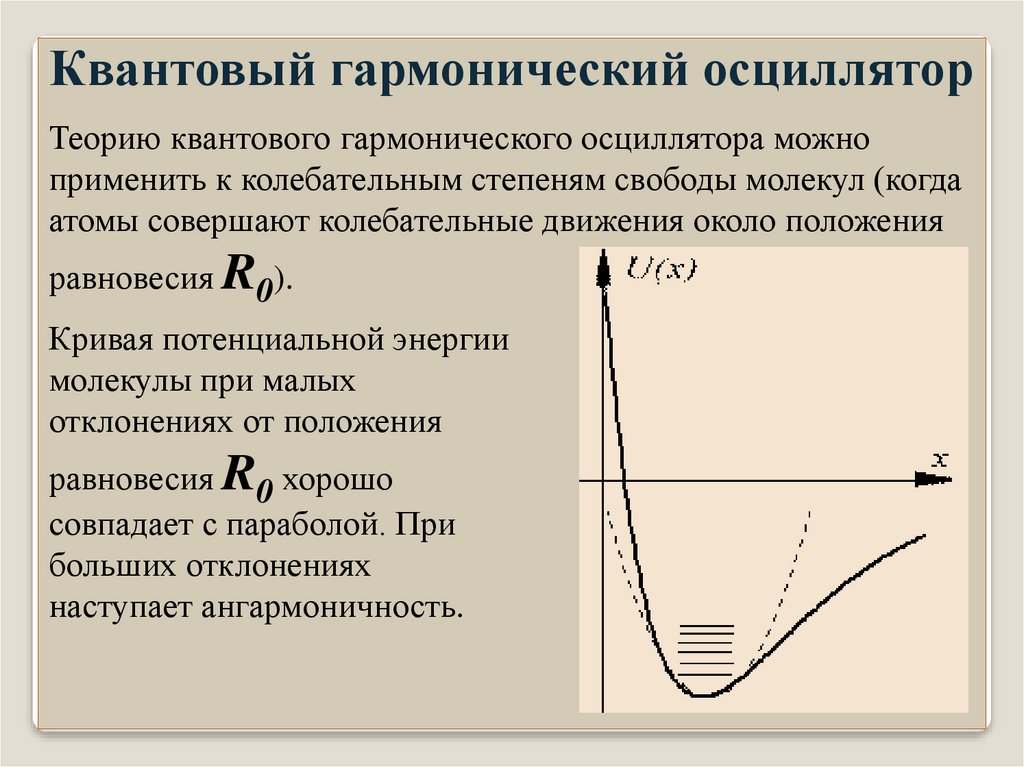
Квантовый гармонический осцилляторТеорию квантового гармонического осциллятора можно
применить к колебательным степеням свободы молекул (когда
атомы совершают колебательные движения около положения
равновесия R0).
Кривая потенциальной энергии
молекулы при малых
отклонениях от положения
равновесия R0 хорошо
совпадает с параболой. При
больших отклонениях
наступает ангармоничность.
22.
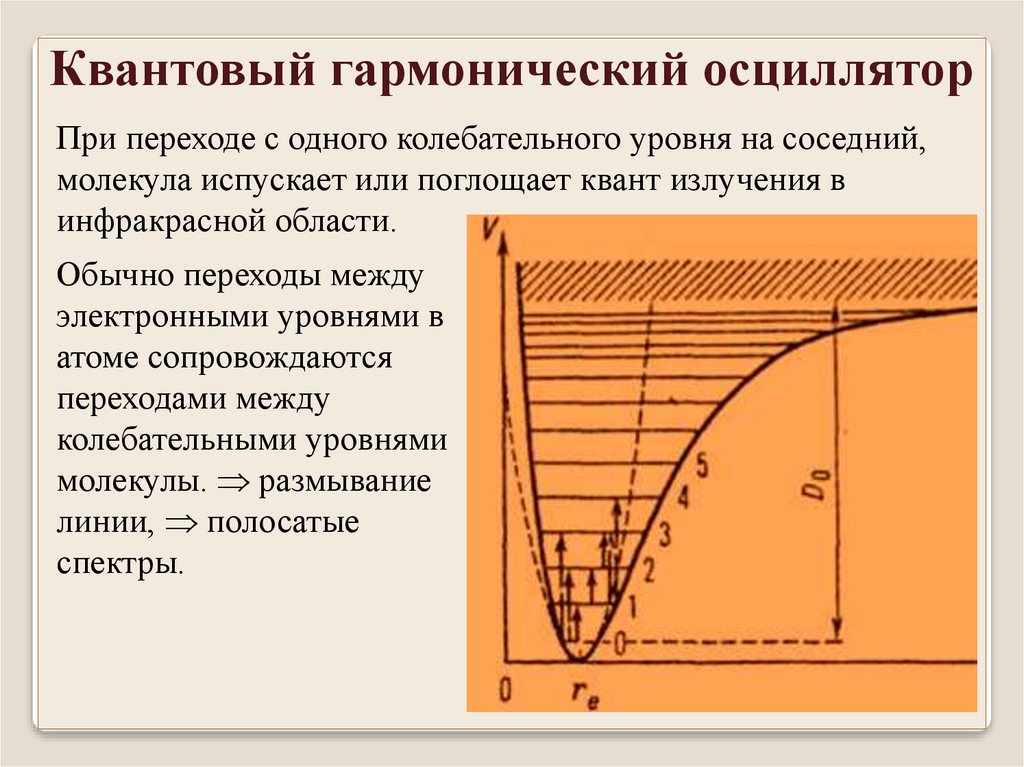
Квантовый гармонический осцилляторПри переходе с одного колебательного уровня на соседний,
молекула испускает или поглощает квант излучения в
инфракрасной области.
Обычно переходы между
электронными уровнями в
атоме сопровождаются
переходами между
колебательными уровнями
молекулы. размывание
линии, полосатые
спектры.
23.
Теплоемкость кристалловПо классической теории
кристалл, состоящий из
N атомов – это система с
3N степенями свободы,
на каждую
колебательную степень
свободы в среднем
приходится энергия kT.
Закон Дюлонга и
Пти: Теплоемкость всех
простых кристаллов
одинакова и равна
3Nk = 3R.
24.
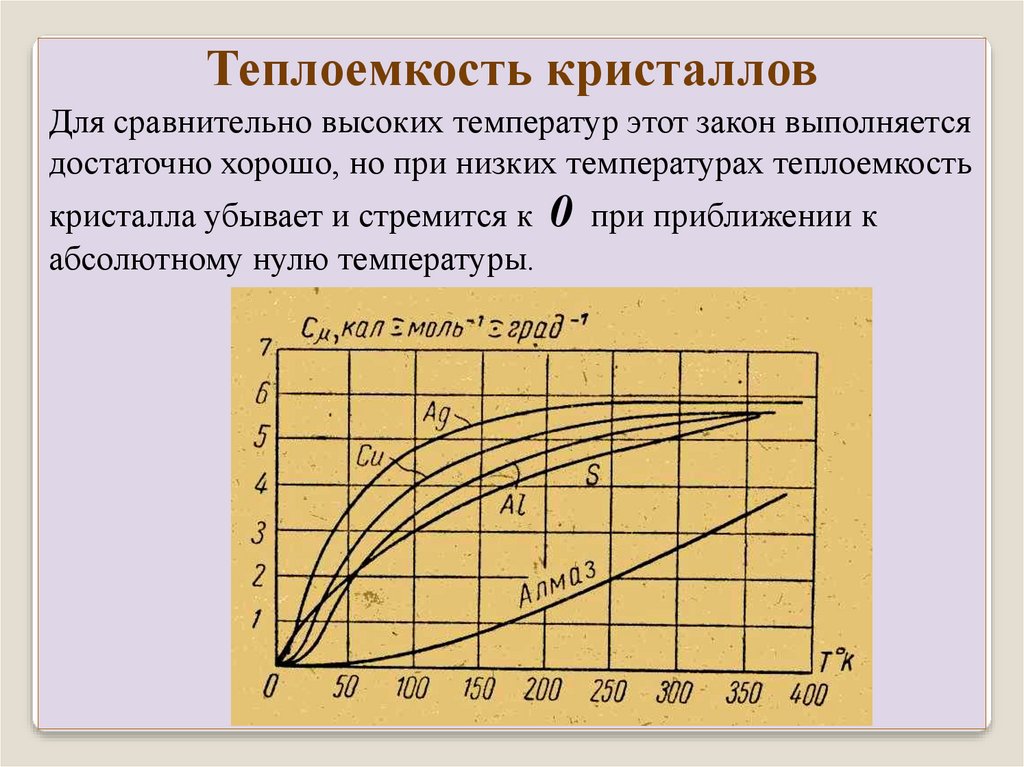
Теплоемкость кристалловДля сравнительно высоких температур этот закон выполняется
достаточно хорошо, но при низких температурах теплоемкость
кристалла убывает и стремится к
абсолютному нулю температуры.
0
при приближении к
25.
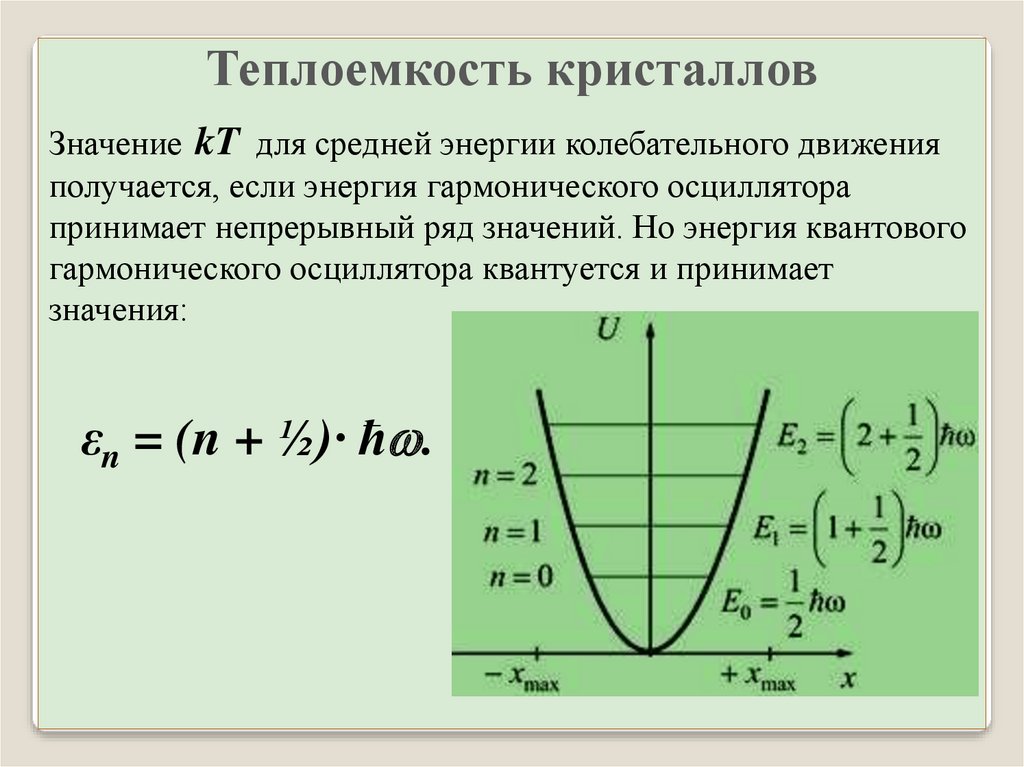
Теплоемкость кристалловЗначение kT для средней энергии колебательного движения
получается, если энергия гармонического осциллятора
принимает непрерывный ряд значений. Но энергия квантового
гармонического осциллятора квантуется и принимает
значения:
εn = (n + ½)· ħ .
26.
Теплоемкость кристалловРаспределение осцилляторов по энергиям подчиняется закону
Больцмана. Среднее значение
n e
e
kT
n
kT
n
kT
1 e
d
kT
ln e
d
kT
1 e kT
2
e
kT
ε
n
kT
по Планку:
d
kT
ln
d
1
e kT
kT
1 e kT
1
1 e
e kT 1
К этому значению надо еще добавить ½· ħ .
kT
e
kT
1
27.
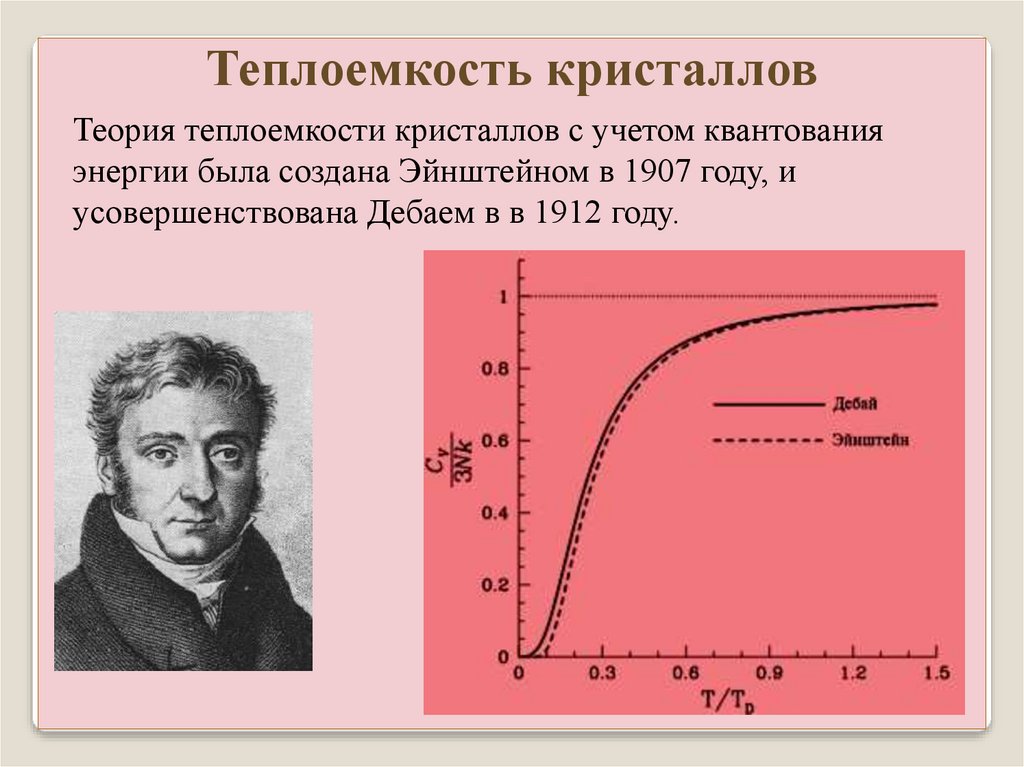
Теплоемкость кристалловТеория теплоемкости кристаллов с учетом квантования
энергии была создана Эйнштейном в 1907 году, и
усовершенствована Дебаем в в 1912 году.
28.
Теплоемкость кристалловПо Эйнштейну кристалл = система 3N независимых
осцилляторов с одинаковой частотой . Слагаемое ½· ħ
тогда еще было неизвестно, и в теории Эйнштейна
отсутствовало. Для внутренней энергии кристалла Эйнштейн
получил выражение:
U 3N
e
kT
а для теплоемкости:
dU
C
3N
e
2
dT
kT
e 1
kT
;
1
kT 2
29.
Теплоемкость кристалловПри высоких температурах:
e
kT
1
e
kT
1
kT
C = 3Nk = 3R
–
и
Закон Дюлонга
и Пти.
При низких температурах: (kT ħ ):
e
kT
1 e
kT
e
C 3N
2
kT
kT
0
при T 0
30.
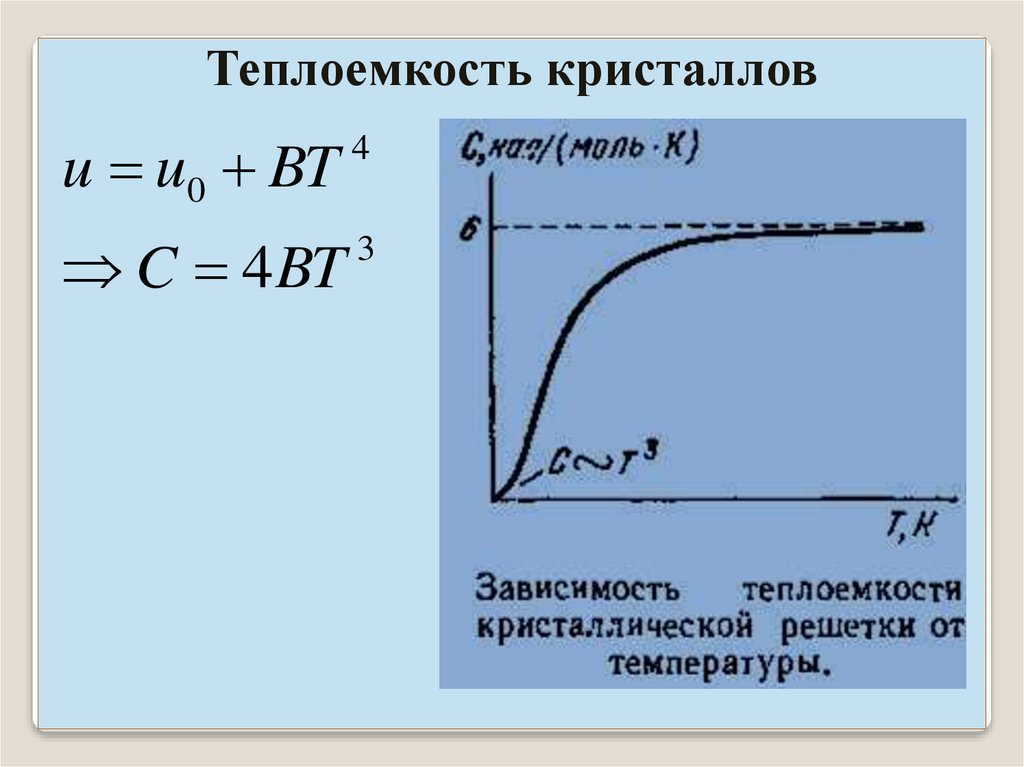
Теплоемкость кристалловОпыты показывают, что теплоемкость стремится к нулю не по
экспоненте, а пропорционально T 3 Теория Эйнштейна дает
лишь качественное совпадение.
Количественного согласия с
опытом удалось добиться
Дебаю, который учел, что
колебания атомов в
кристаллической решетке не
являются независимыми.
31.
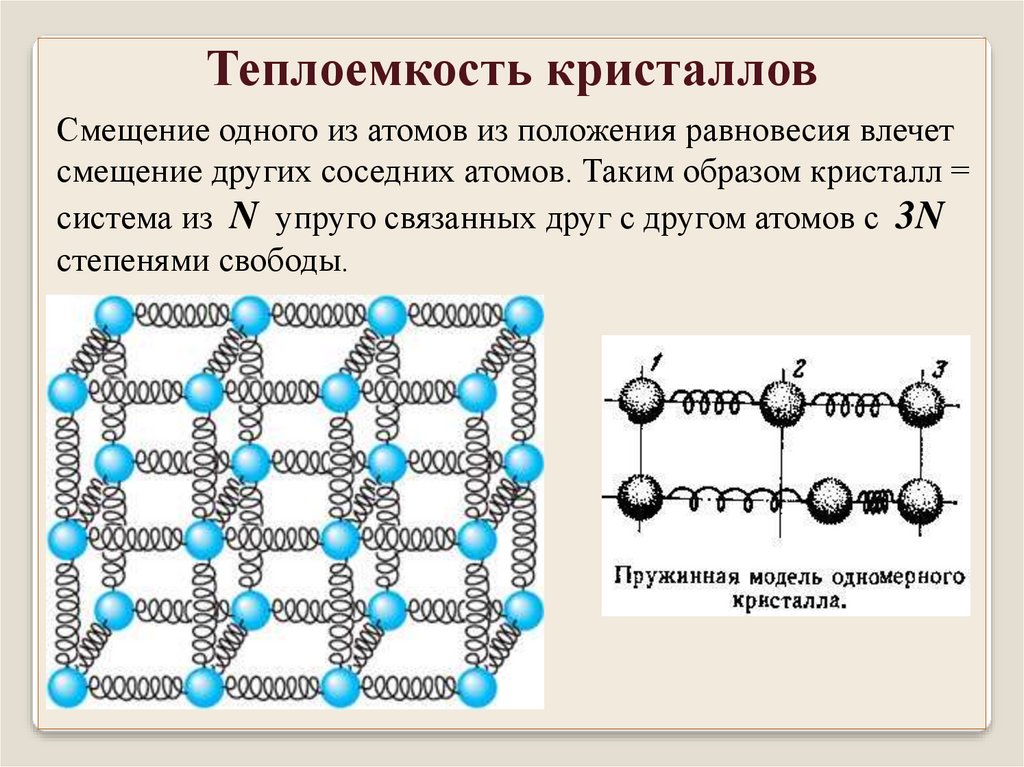
Теплоемкость кристалловСмещение одного из атомов из положения равновесия влечет
смещение других соседних атомов. Таким образом кристалл =
система из N упруго связанных друг с другом атомов с 3N
степенями свободы.
32.
Теплоемкость кристалловПример: система из трех
одинаковых шаров,
соединенных
невесомыми пружинами,
концы которых
закреплены. Если шары
могут перемещаться
только по оси «y», то
система обладает тремя
степенями свободы. А
всего (если шары
перемещаются по всем
осям) – 9 степеней
свободы.
33.
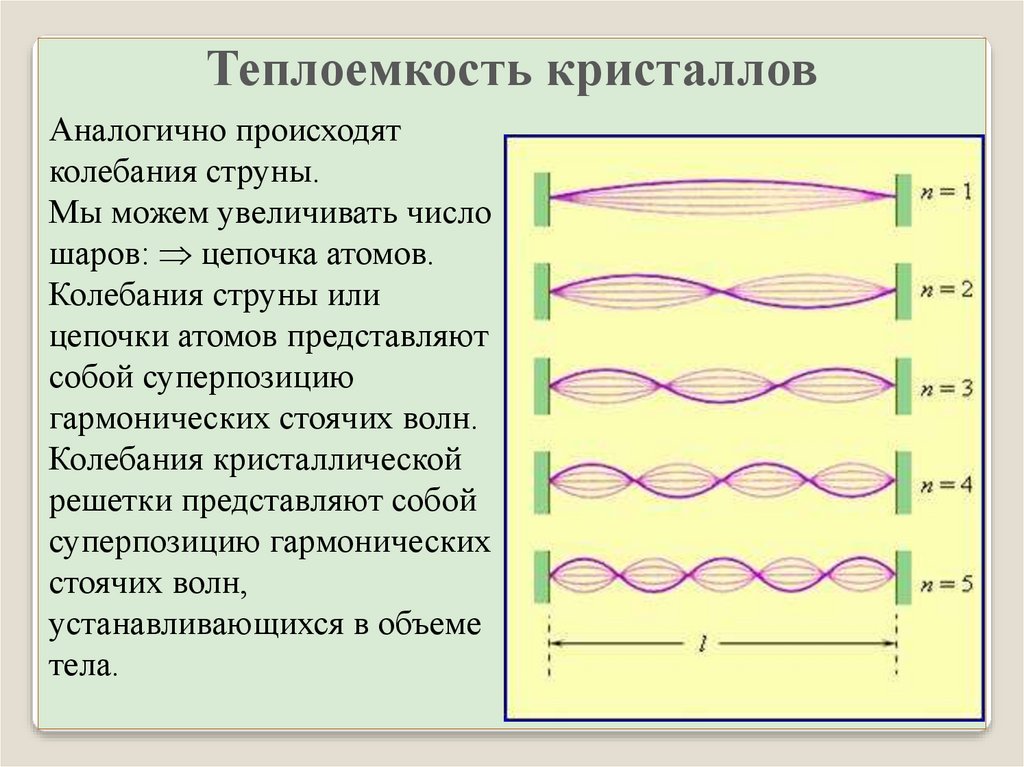
Теплоемкость кристалловАналогично происходят
колебания струны.
Мы можем увеличивать число
шаров: цепочка атомов.
Колебания струны или
цепочки атомов представляют
собой суперпозицию
гармонических стоячих волн.
Колебания кристаллической
решетки представляют собой
суперпозицию гармонических
стоячих волн,
устанавливающихся в объеме
тела.
34.
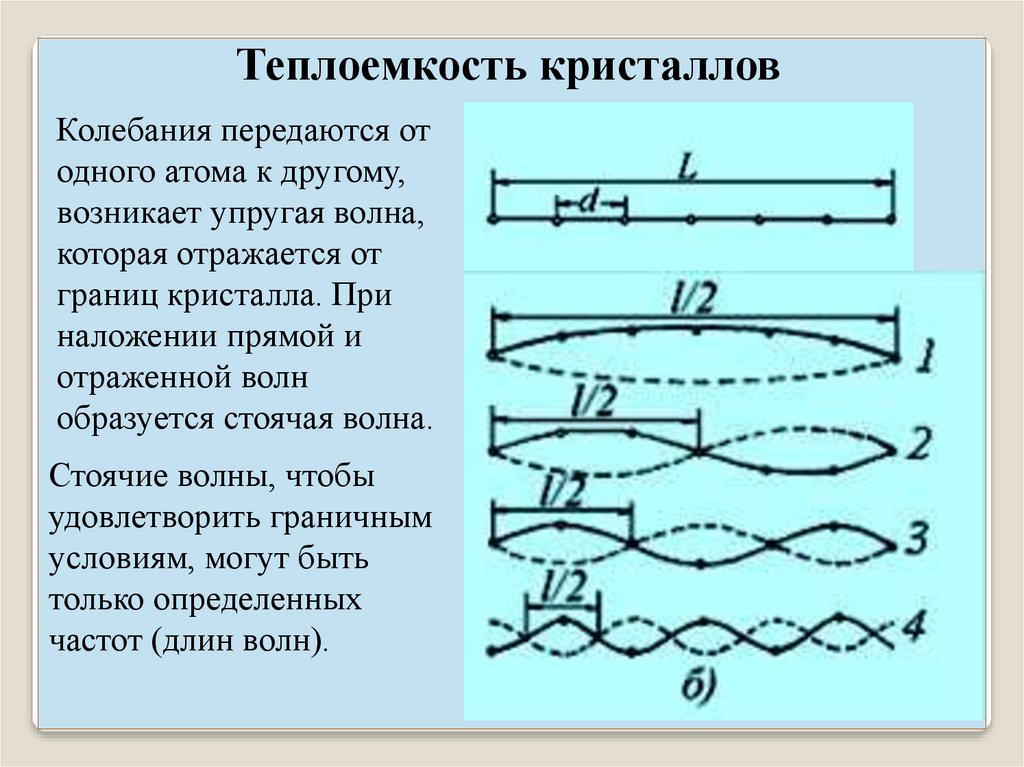
Теплоемкость кристалловКолебания передаются от
одного атома к другому,
возникает упругая волна,
которая отражается от
границ кристалла. При
наложении прямой и
отраженной волн
образуется стоячая волна.
Стоячие волны, чтобы
удовлетворить граничным
условиям, могут быть
только определенных
частот (длин волн).
35.
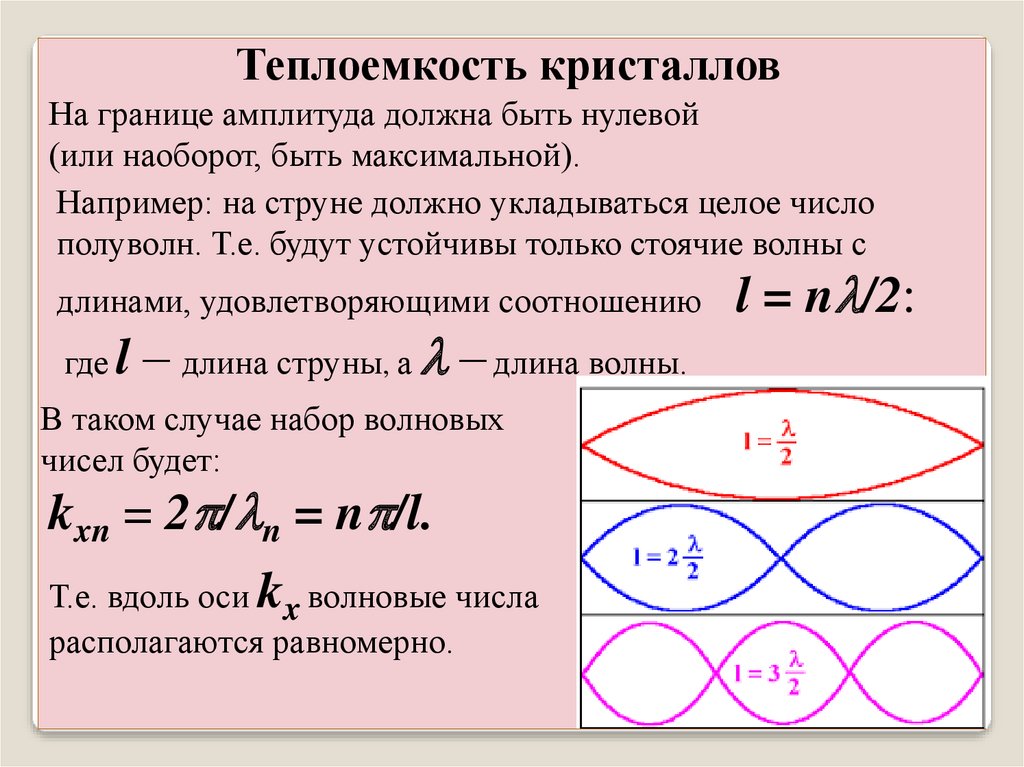
Теплоемкость кристалловНа границе амплитуда должна быть нулевой
(или наоборот, быть максимальной).
Например: на струне должно укладываться целое число
полуволн. Т.е. будут устойчивы только стоячие волны с
длинами, удовлетворяющими соотношению
где l
– длина струны, а – длина волны.
В таком случае набор волновых
чисел будет:
kxn = 2p/ n = np/l.
Т.е. вдоль оси kx волновые числа
располагаются равномерно.
l = n /2:
36.
Теплоемкость кристалловОтраженным волнам соответствуют точки на отрицательной
части оси kx.
На струне накладываются две волны с векторами kx и –kx;
на плоскости – четыре (kx , –kx)×(ky , –ky);
в объеме – восемь волн.
В пространстве с осями: kx , ky ,kz каждой стоячей волне
отвечает точка одном октанте (точки в других октантах
отвечают отраженным волнам). Точки располагаются
равномерно.
kxn = n1p/a,
kyn = n2p/b,
kzn = n3p/c.
На каждую точку приходится объем:
dkxdkydkz= p3/abc = p3/V
37.
Теплоемкость кристалловПлотность волновых точек в k ̶ пространстве: rТ = V/p3
Число стоячих волн с модулем волнового числа от k до
k + dk (т.е. в одной восьмой части шарового слоя в k
пространстве):
2
V 1
k dk
2
dN k 3 4pk dk V
2
p 8
2p
Или
d
dN V
2 3
2p v
2
Здесь v – фазовая скорость
волны в кристалле (для
электромагнитной волны = c).
38.
Теплоемкость кристалловОбъем кристалла V входит в виде сомножителя. на
единицу объема приходится волн.
2
d
dN 2 3
2p v
С учетом всех видов поляризации:
Для электромагнитного излучения:
2d
dN 2 3
p v
2d 2 1
3
Для упругой волны в кристалле: dN
2
3
2p v v
2
3
d
Если v = v||:
dN
2 3
2p v
||
39.
Теплоемкость кристалловN dN
Количество всех волн:
Для электромагнитных волн
N dN
0
m
Для упругих волн
m
3 2d
m3
N dN
2 3 3n
2 3
2p v
2p v
0
0
Полное число степеней свободы – 3n
m v3 6p 2 n
40.
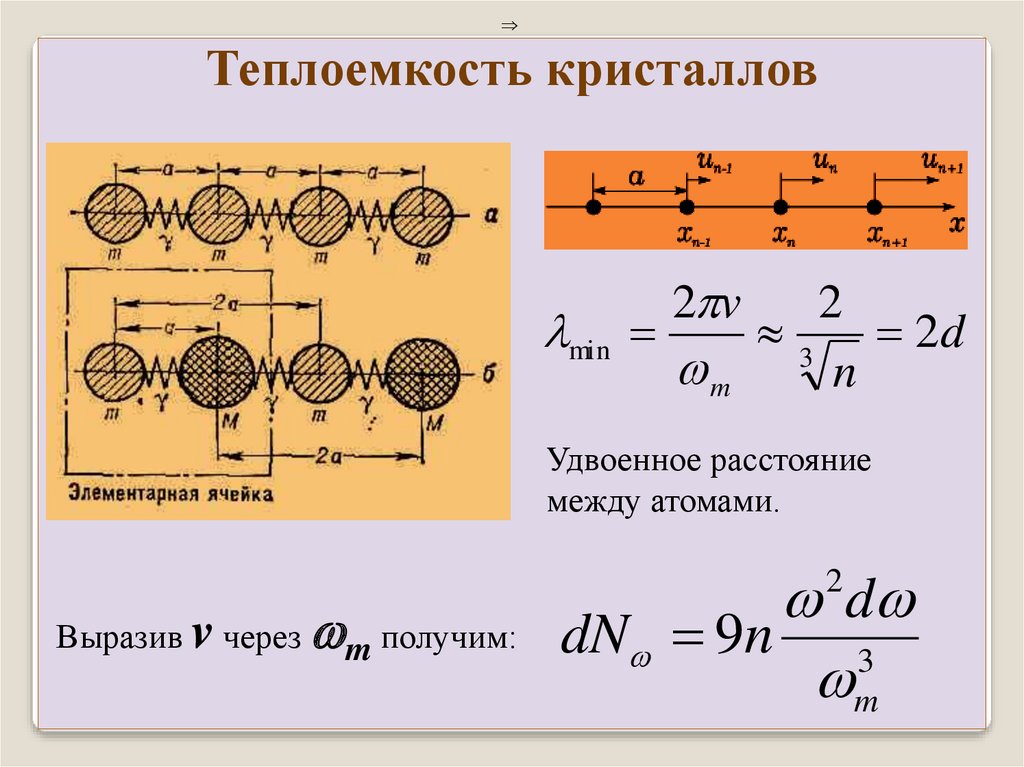
Теплоемкость кристалловmin
2pv
m
2
3 2d
n
Удвоенное расстояние
между атомами.
Выразив v через m получим:
d
dN 9n 3
m
2
41.
Теплоемкость кристалловu dN
Плотность энергии:
Для электромагнитного
излучения:
2 d
u 2 3
p c kT
0
e
kT
2 3
p c
4
1
x3dx 4 4
0 e x 1 c T
Для упругих волн:
1
2 d
u 3
m 0 2
e kT 1
9n
m
3
u0 2 3
2p v
m
3
0
3 kT
u0 2 3
2p v
e
kT
4 m
d
1
x 3dx
4
u
BT
0 e x 1 0
42.
Теплоемкость кристалловu u0 BT
4
C 4BT
3
43.
Теплоемкость кристалловХарактерная температура Дебая: Q
kQ = ħ max Q = ħ max/k
указывает для каждого вещества ту область, где квантовые
эффекты становятся существенными.
m
1;
При T Q
e
m
kT
m
1
; u u0 3nkT
kT
kT
Т.е C = 3NAk – закон Дюлонга и Пти.
44.
Теплоемкость кристаллов45.
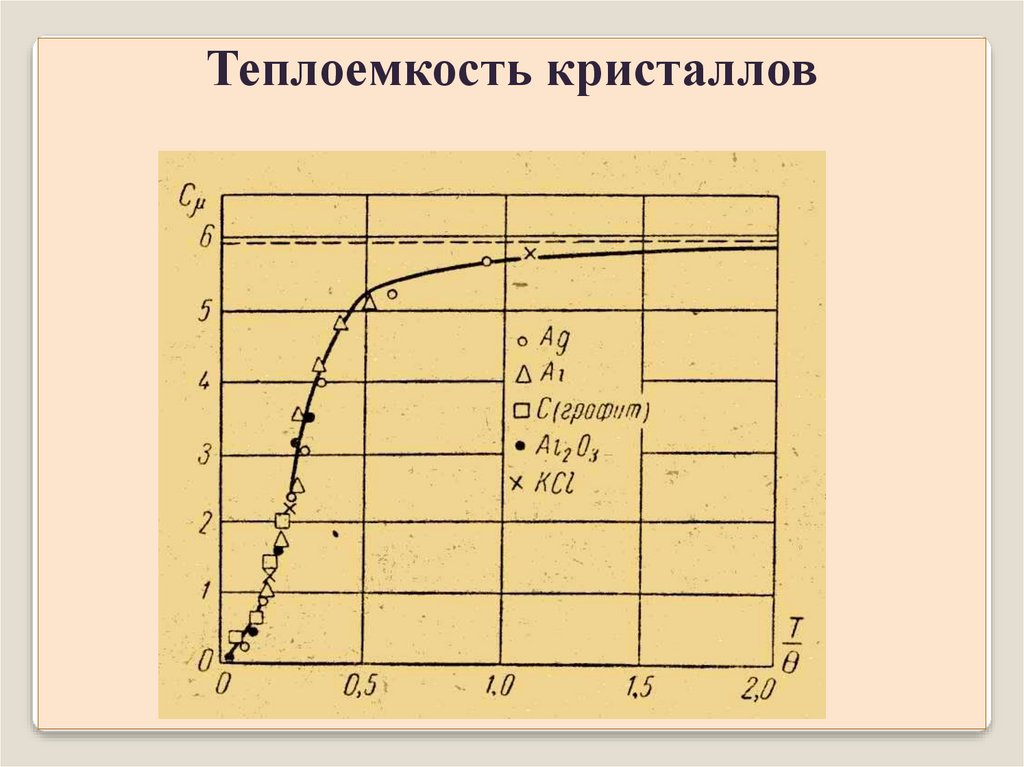
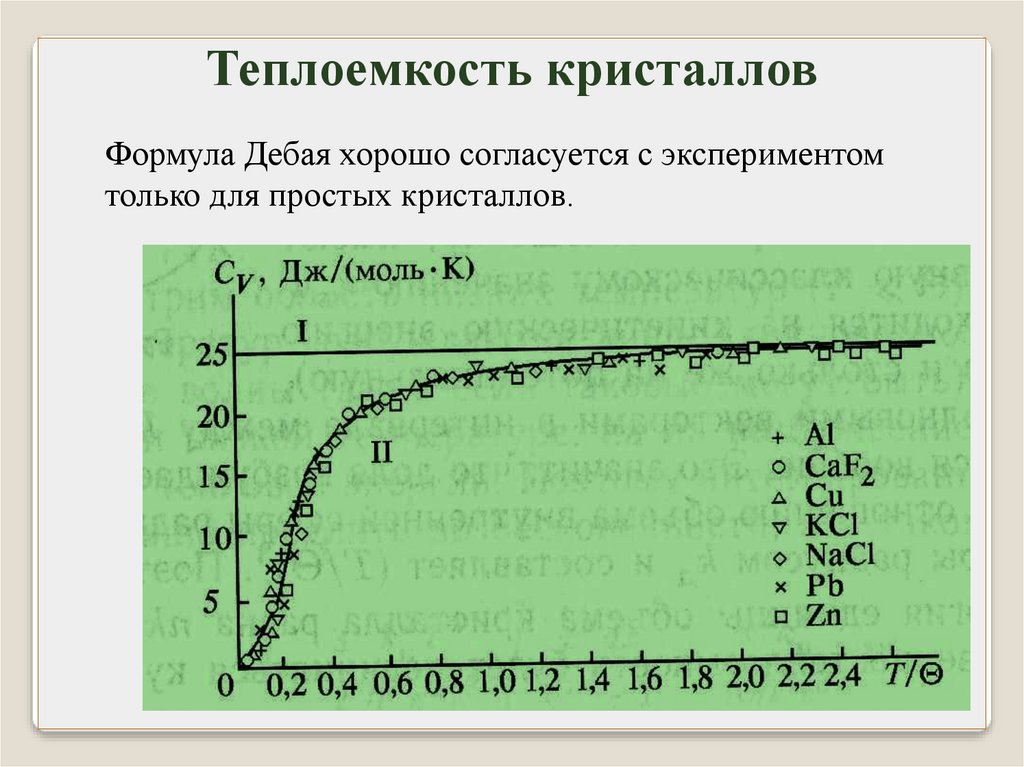
Теплоемкость кристалловФормула Дебая хорошо согласуется с экспериментом
только для простых кристаллов.
46.
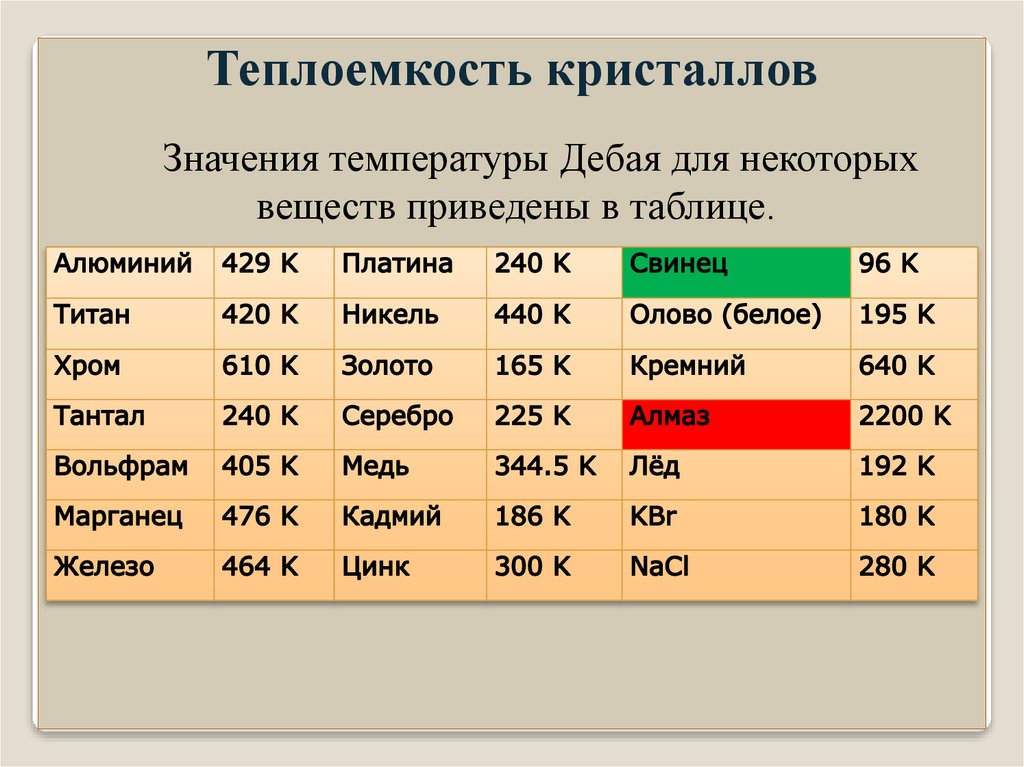
Теплоемкость кристалловЗначения температуры Дебая для некоторых
веществ приведены в таблице.
47.
Фотоны и фононыЗа вычетом энергии нулевых колебаний, энергия нормального
колебания частоты i слагается из порций: εi = ħ i . Эта
порция (квант) энергии называется фононом, по аналогии с
квантом электромагнитного излучения = фотоном.
Многие процессы в кристалле
протекают так, как если бы
фонон обладал импульсом
p k ;
p k
v
Фонон ведет себя так, как если бы он
был частицей с энергией и импульсом.
48.
Фотоны и фононыВ отличие от фотона, фонон не может существовать в
вакууме. Для его существования необходима среда. Поэтому
фонон называют квазичастицей.
При взаимодействии фононов их импульс может
передаваться кристаллу не сохраняется квазиимпульс.
Колебания кристаллической
решетки можно представить как
фононный газ в пределах кристалла
подобно электромагнитному
излучению в полости фотонный
газ.

























 Физика
Физика