Похожие презентации:
Способы решения квадратных уравнений
1. Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 1 им. З.Я. Лавровского станицы
Ленинградскоймуниципального образования Ленинградский район
Урок обобщающего разноуровневого повторения
9классе.
Учитель математики Филобок Т.В.
2. ЦЕЛЬ УРОКА:
Обобщение и систематизация знанийпо теме
«Способы решения квадратных
уравнений»
3. ЗАДАЧИ УРОКА:
отработка способов решения квадратных уравнений;выработка умения выбирать наиболее рациональный способ
решения;
развитие логического мышления, памяти, внимания, умения
сравнивать и обобщать;
проверка уровня усвоения темы путем дифференцированного
опроса уч-ся;
воспитание навыков контроля и самоконтроля;
подготовка содержательной базы для краевых
диагностических работ и успешной сдачи ГИА, ЕГЭ .
4.
5.
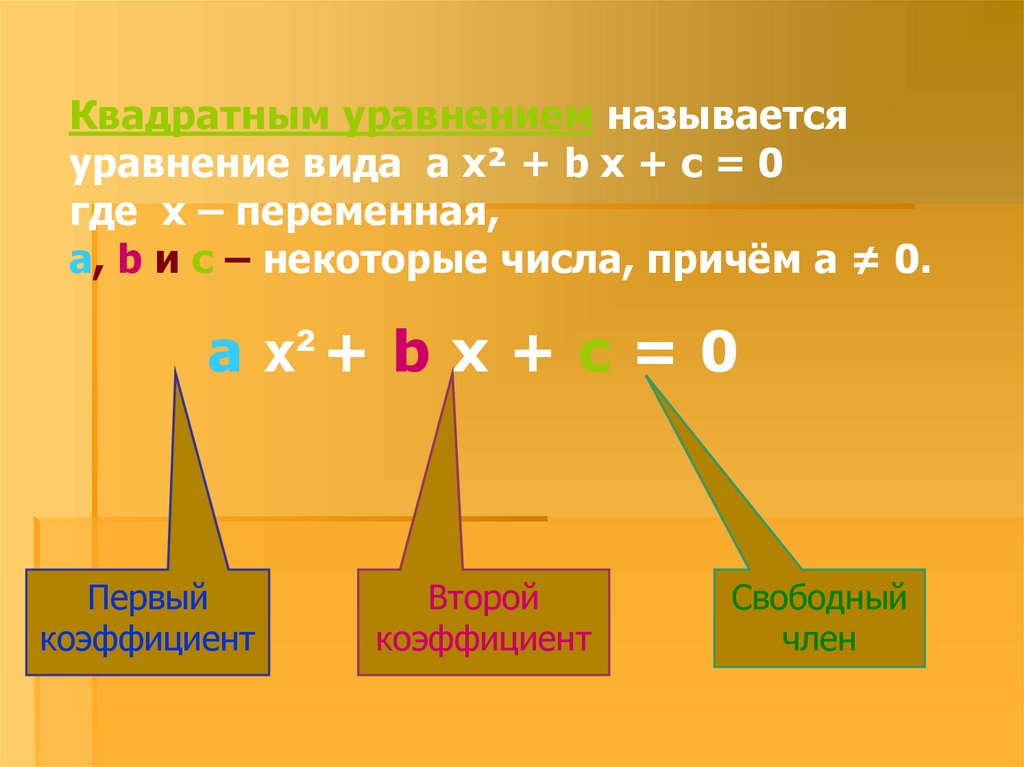
Квадратным уравнением называетсяуравнение вида a x² + b x + c = 0
где х – переменная,
a, b и c – некоторые числа, причём а ≠ 0.
a x² + b x + c = 0
Первый
коэффициент
Второй
коэффициент
Свободный
член
6.
Классификация .Квадратные уравнения.
b = 0;
a x² + c = 0
неполное
полное
а х² + в х + с = 0
приведённое
x² + p x + q = 0
c = 0;
a x² + b x = 0
b = 0; c = 0;
a x² = 0
7.
Здесь вы видите уравнения, определённые по какому-то признаку.Как вы думаете, какое из уравнений этой группы является
лишним?
1. x² – 9x = 0,
1. x² – 5x + 1 = 0,
2. 4x² – х – 3 = 0,
2. x² + 3x – 5 = 0,
3. 16 – x² = 0,
3. 2x² – 7x – 4 = 0,
4. 4x² = 0.
4. x² + 2x = 1 = 0.
1. 5x² – 2x – 3 = 0,
2. x² + 2x – 35 = 0,
3. 2x² + 9x – 11 = 0,
4. x² – 6x + 5 = 0.
8.
«ДИСКРИМИНАНТ» - РАЗЛИЧИТЕЛЬ.Д = в² - 4 а с
Д>0
Д=0
Д<0
Уравнение имеет
два действительных
корня.
х1 = (- в- √ Д )/ 2а
х2= (- в + √ Д )/2а
Уравнение имеет
два равных
действительных корня.
х1,2 = - в / 2а
Уравнение не имеет
корней.
9.
Самостоятельная работа.Вариант 1.
Вариант 2.
1. 3х² – 27 = 0;
4. 4х² – 20х = 0;
2. х² – 5х – 6 = 0;
5.
х² – 1 = 8х(х + 1).
3. 2х² = 4 – 7х.
Вариант 3.
6.
х² –х – 30 = 0;
7. 5х(х – 3) = 3х – 16.
6
2
5
7
4
1
3
Ш
Т
И
Ф
Е
Л
Ь
10.
Штифель (1486 – 1567)в 1544 году сформировал общее
правило решения квадратных уравнений, приведённых к единому
каноническому виду
x^2 + bx = c
при всевозможных комбинациях знаков и коэффициентов b и c.
Франсуа Виет (1540 – 1603) вывел формулы решения
квадратного уравнения в общем виде, однако он признавал только
положительные числа.
Итальянские учёные Тарталья, Кардано, Бомбелли
среди первых в XVI веке учитывают, помимо положительных, и
отрицательные корни.
В XVII веке благодаря трудам Жиррара,
Декарта, Ньютона
и других учёных, способ решения квадратных уравнений принимает
современный вид.
11.
Франсуа Виет(1540 – 1603)
Париж
12.
Теорема Виета.Если х1 и х2 корни приведённого квадратного
уравнения х² + px + q = 0,
то x1 + x2 = - p,
а
x1 x2 = q.
Обратное утверждение:
Если числа m и n таковы, что m + n = - p,
mn = q, то эти числа являются корнями
уравнения х² + px + q = 0.
Обобщённая теорема:
Числа х1 и х2 являются корнями приведённого
квадратного уравнения х² + px + q = 0
тогда
и только тогда, когда x1 + x2 = - p, x1 x2 = q.
Следствие: х²+ px + q = (х – х1)(х – х2)
13.
Ситуации, в которых можетиспользоваться теорема Виета.
Проверка правильности найденных корней.
Определение знаков корней квадратного уравнения.
Устное нахождение целых корней приведённого
квадратного уравнения.
Составление квадратных уравнений с заданными
корнями.
Разложение квадратного трёхчлена на множители.
14.
Решите следующие задания:1. Верно ли, что числа 15 и 7 являются корнями уравнения
x² – 22x + 105 = 0 ?
2. Определите знаки корней уравнения x² + 5x – 36 = 0.
3. Найдите устно корни уравнения x² – 9x + 20 = 0.
4. Составьте квадратное уравнение, корнями которого
являются числа 1/3 и 0,3.
5. Разложите квадратный трёхчлен
множители.
x² + 2x – 48
на
15.
Приёмы устного решенияквадратных уравнений.
a x² + b x + c = 0.
Обоснование:
f (x) = a x ² + b x + c ;
f (1) = a + b + c; f (- 1) = a - b + c.
1.Если a + b + c = 0, то один корень
уравнения x = 1, а второй x = c/a.
2.Если a - b + c = 0, то один корень
уравнения x = - 1, а второй x = - c/a.
16.
Решите уравнения, используя свойствакоэффициентов:
1.2x² + 3x + 1 = 0;
2.5x² – 4x – 9 = 0;
3.7x² + 2x – 5 = 0;
4.X² + 17x – 18 = 0;
5.100x² – 97x – 197 = 0.
17.
Домашнее задание:1. Решите 9 уравнений
своего варианта.
Отметьте в координатной
плоскости результаты .
2. Решите уравнение
18. Главный принцип нашей работы:
19. Домашнее задание.
Вариант 1.1.
2х² – 16x = 0,
Вариант 2.
(x2 ; x1 );
2х² + 16x = 0,
(x1 ;x2);
х² – 12x + 27 = 0,
(x2 ; x1 );
3.
2х² – 6x – 56 = 0,
(x2 ; x1 );
4.
х² + 9x + 20 = 0,
(x1 ;x2);
5.
х² + 8x = 0,
(x1 ;x2);
6.
х² – 14x + 40 = 0,
(x1 ;x2);
7.
3х² – 18x + 15 = 0, (x1 ;x2);
8.
4х² – 24x + 32 = 0, (x1 ;x2);
9.
х² – 3x + 2,25 = 0, (x1 ;x2);
1.
2.
5х² – 50x = 0,
(x2 ; x1 );
2.
3.
х²– 4x – 32 = 0,
(x2 ; x1 );
4.
х²+ 12x + 32 = 0, (x1 ;x2);
5.
х²+ 11x – 26 = 0, (x1 ;x2);
6.
5х² – 40x = 0,
7.
х²– 11x + 24 = 0, (x2 ; x1 );
8.
4х² – 12x – 40 = 0, (x1 ;x2);
9.
2х² + 13x – 24 = 0, (x1 ;x2).
(x2 ; x1 );
20. Проверьте своё настроение !!!
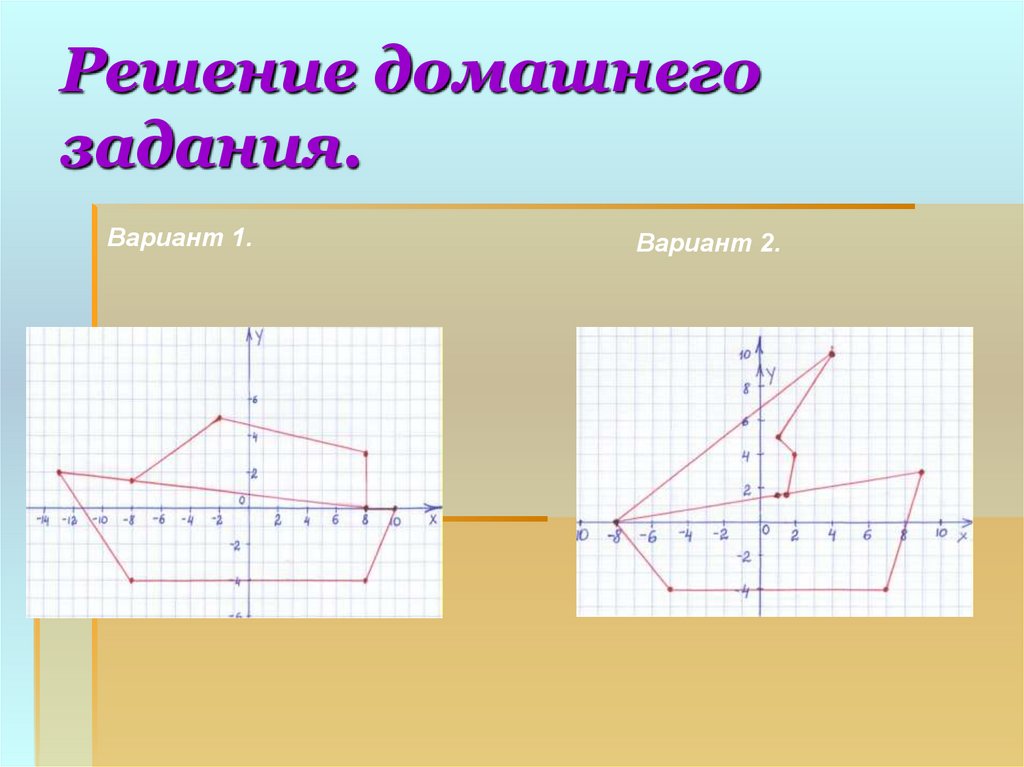
21. Решение домашнего задания.
Вариант 1.Вариант 2.



















 Математика
Математика








