Производная функции

1.

Мы продолжаем изучать тему
«Производная функции»
Мы познакомимся с применением
производной для исследования
свойств функции
Желаю успехов
в изучении темы!

2. Применение производной к исследованию функции.

у = f (х)
)
у
))
х
Возрастание и убывание
функции.

3.

Повторение:
~ определение возрастающей и убывающей функций
~ геометрический смысл производной
Изучение нового материала:
~ установление зависимости между характером
монотонности функции и знаком её производной
~ алгоритм нахождения промежутков
монотонности функции
~ решение заданий

4. 1. Монотонность функции.

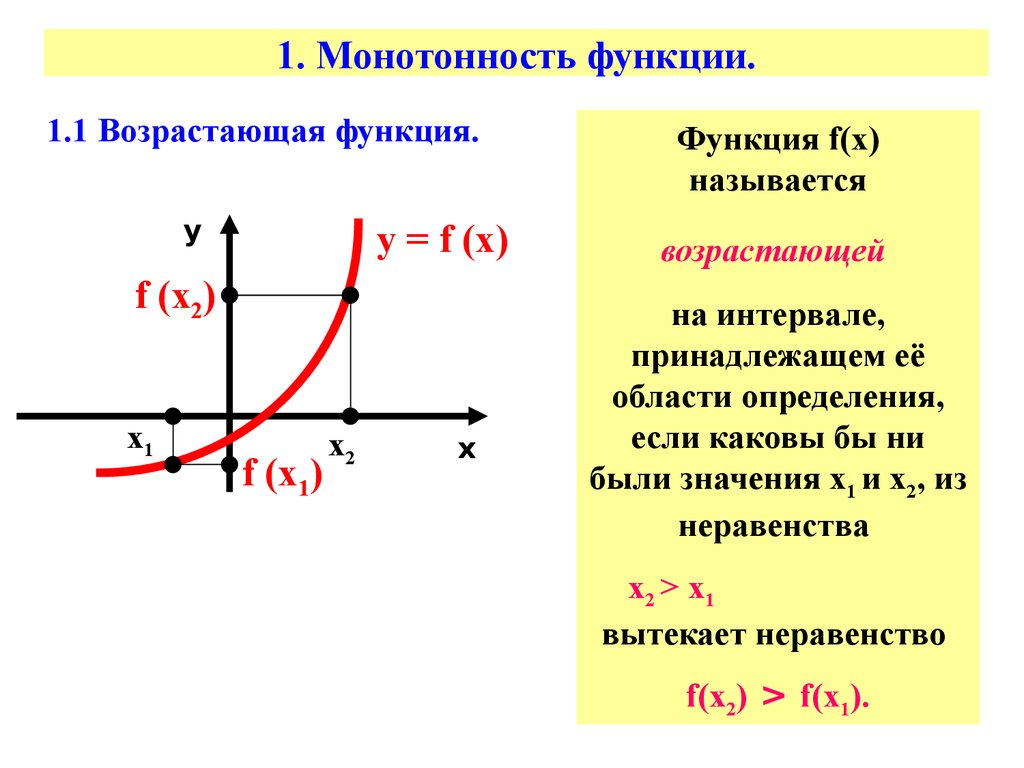
1.1 Возрастающая функция.
у
у = f (х)
f (х2)
х1
f (х1)
х2
х
Функция f(х)
называется
возрастающей
на интервале,
принадлежащем её
области определения,
если каковы бы ни
были значения х1 и х2, из
неравенства
х2 > х1
вытекает неравенство
f(х2) > f(х1).

5. 1. Монотонность функции.

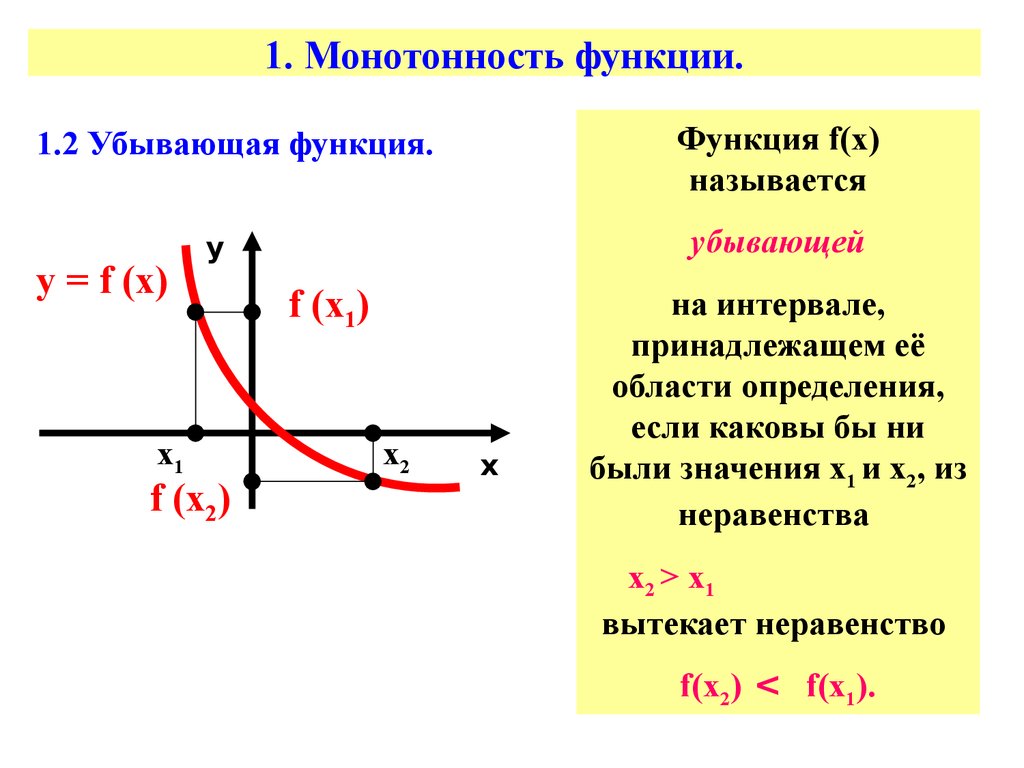
Функция f(х)
называется
1.2 Убывающая функция.
у = f (х)
х1
убывающей
у
f (х2)
f (х1)
х2
х
на интервале,
принадлежащем её
области определения,
если каковы бы ни
были значения х1 и х2, из
неравенства
х2 > х1
вытекает неравенство
f(х2) < f(х1).

6. 1. Монотонность функции.

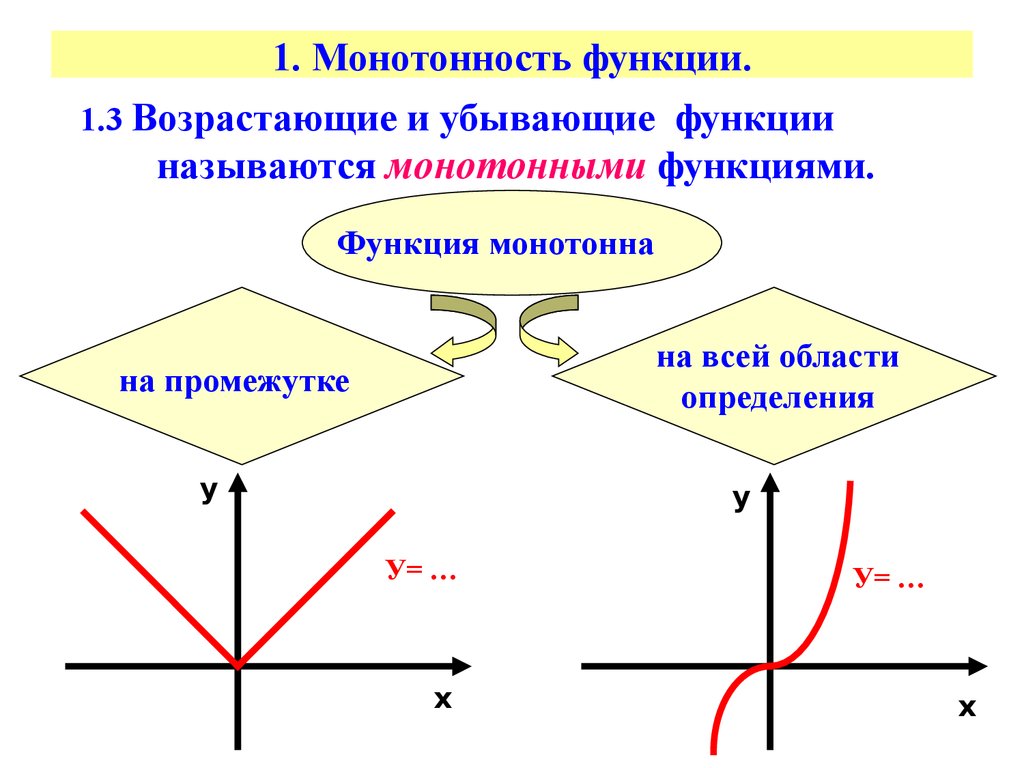
1.3 Возрастающие и убывающие функции
называются монотонными функциями.
Функция монотонна
на всей области
определения
на промежутке
у
у
У= …
х
У= …
х

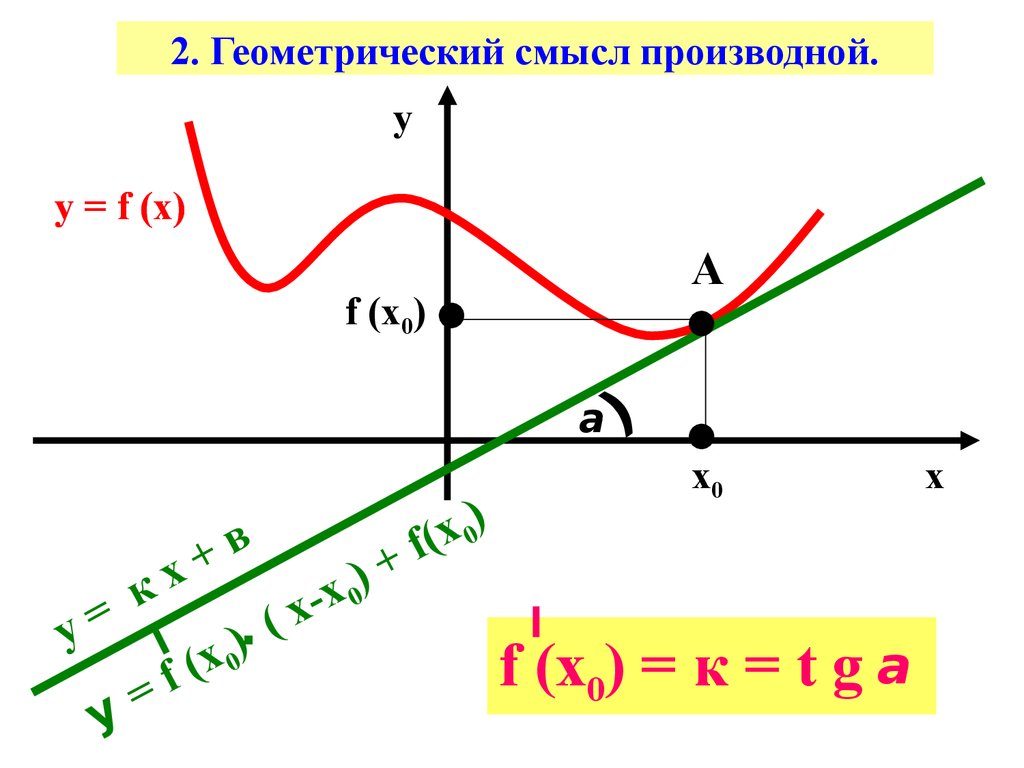
7. 2. Геометрический смысл производной.

у
у = f (х)
А
f (х0)
а
у=
к
=
у
в
+
х
.(
)
f (х 0
+
)
0
х
х
)
0
х
f(
)
х0
f (х0) = к = t g а
х

8.

Вы умеете
с помощью графика функции
определять промежутки монотонности функции
Можно ли без построения
графика функции
определять характер
монотонности функции?

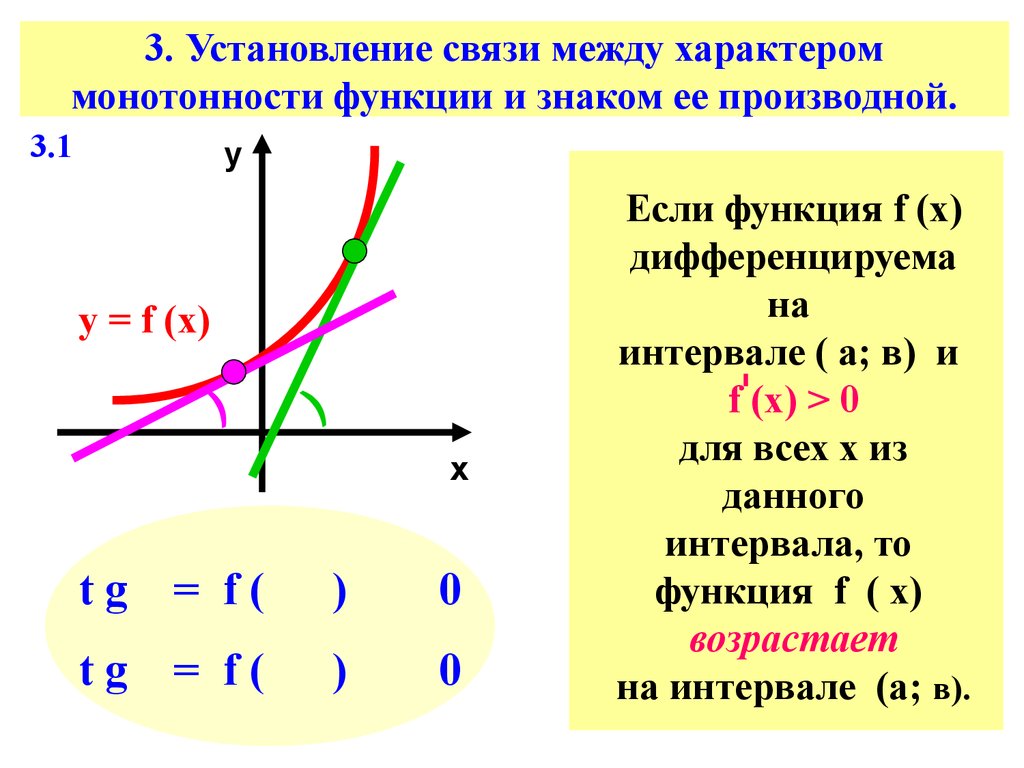
9. 3. Установление связи между характером монотонности функции и знаком ее производной.

3.1
у
у = f (х)
)
)
х
tg
= f(
)
0
tg
= f(
)
0
Если функция f (х)
дифференцируема
на
интервале ( а; в) и
f (х) > 0
для всех х из
данного
интервала, то
функция f ( х)
возрастает
на интервале (а; в).

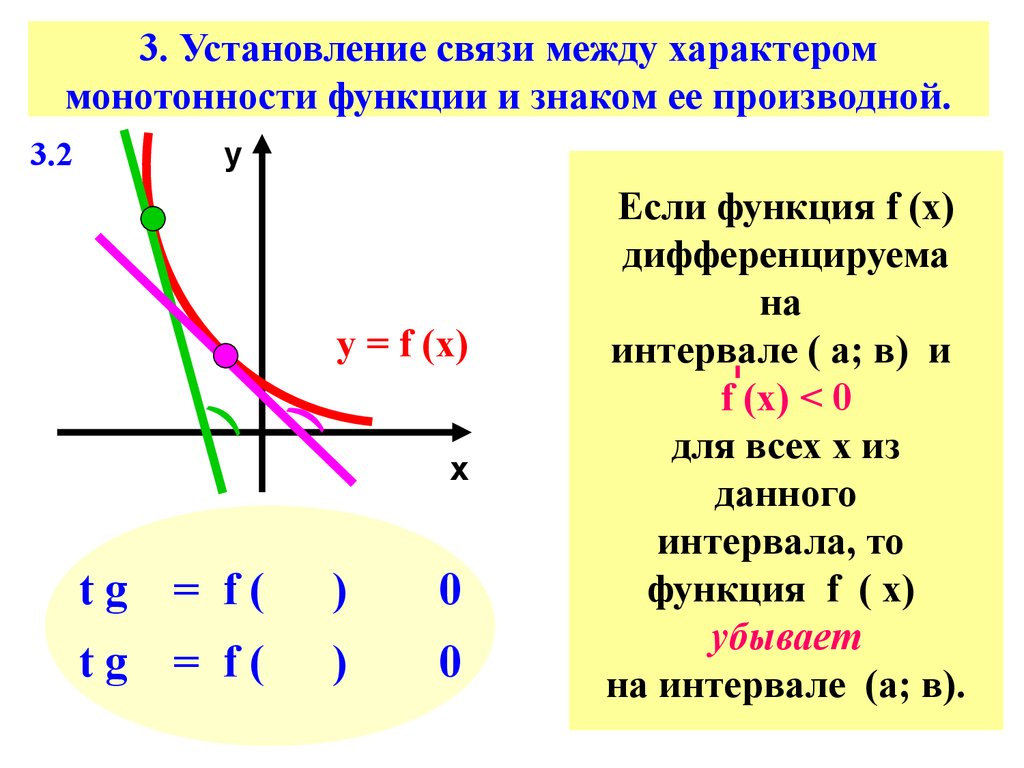
10. 3. Установление связи между характером монотонности функции и знаком ее производной.

у
3.2
)
)
у = f (х)
х
tg
= f(
)
0
tg
= f(
)
0
Если функция f (х)
дифференцируема
на
интервале ( а; в) и
f (х) < 0
для всех х из
данного
интервала, то
функция f ( х)
убывает
на интервале (а; в).

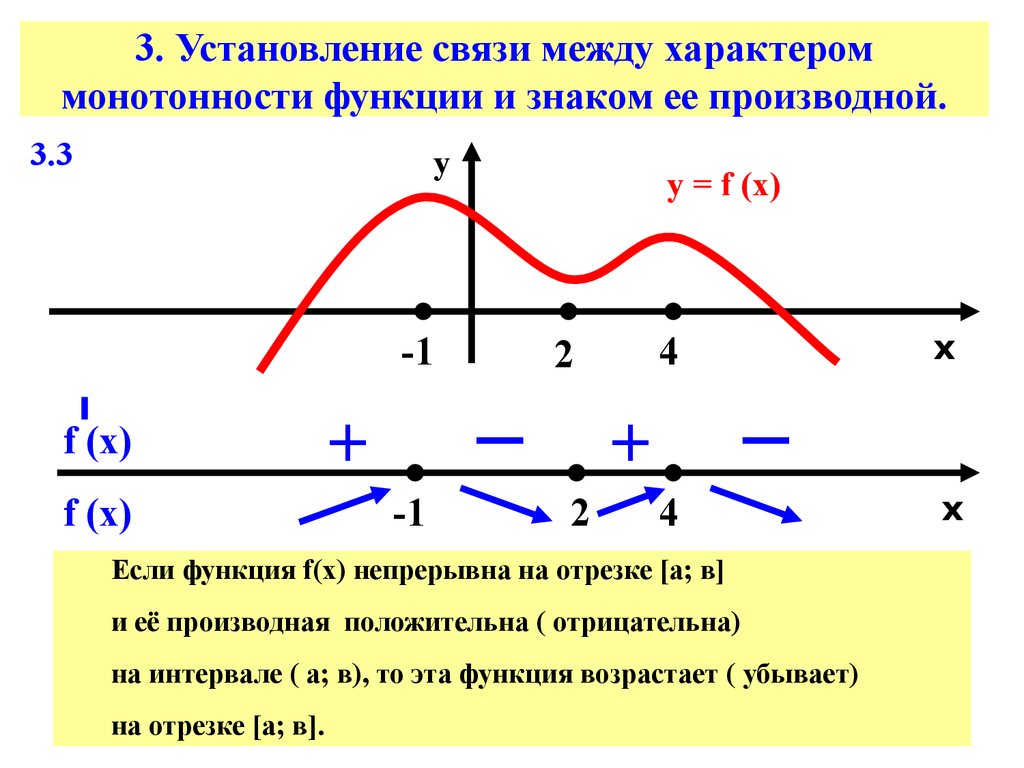
11. 3. Установление связи между характером монотонности функции и знаком ее производной.

3.3
у
-1
f (х)
f (х)
у = f (х)
2
+
4
х
4
х
+
-1
2
Если функция f(х) непрерывна на отрезке [а; в]
и её производная положительна ( отрицательна)
на интервале ( а; в), то эта функция возрастает ( убывает)
на отрезке [а; в].

12. 3. Установление связи между характером монотонности функции и знаком ее производной.

3.4
у
у = f (х)
-1
f (х)
2
+
f (х)
х
4
х
+
-1
2
Функция возрастает: х
Функция убывает:
4
(
х
]
[
]
[
]
[
)

13. 3. Установление связи между характером монотонности функции и знаком ее производной.

3.5
Алгоритм нахождения промежутков
монотонности функции.
1. Найти область определения функции.
2. Найти производную функции.
3. Найти значения аргумента,
при которых значение производной
больше нуля, меньше нуля.
4. Сделать вывод.

14. 4. Решение заданий.

4.1
f(х) = х 4 - 2 х 2
1. Д(f) :
2. f (х) =
3. f (х) > 0, f (х) < 0
f (х)
f (х)
4. Функция возрастает:
Функция убывает:
х

15. 4. Решение заданий.

4.2
f(х) =1/ (х+2)
1. Д(f) :
2. f (х) =
3. f (х) > 0, f (х) < 0
f (х)
f (х)
4. Функция возрастает:
Функция убывает:
х

16. 4. Решение заданий.

4.3
f(х) = х +4/х
1. Д(f) :
2. f (х) =
3. f (х) > 0, f (х) < 0
f (х)
f (х)
4. Функция возрастает:
Функция убывает:
х

17.

Итоги урока
возрастающая функция
убывающей функций
геометрический смысл производной
зависимость между характером
монотонности функции и знаком её производной
алгоритм нахождения промежутков
монотонности функции

18.

Желаю всем
успехов в изучении темы!