Решение задания В8. Основные типы заданий

1. Решение задания В8

Основные типы заданий

2.

Тип задачи
(дано. Найти)
План решения
Дан график
1.
производной,
найти
количество
точек, в
которых
2.
касательная
совпадает или
параллельна
прямой
у=kх+b
Найти точку
на графике
производной
с ординатой
равной k
Определить
количество
таких точек
пример
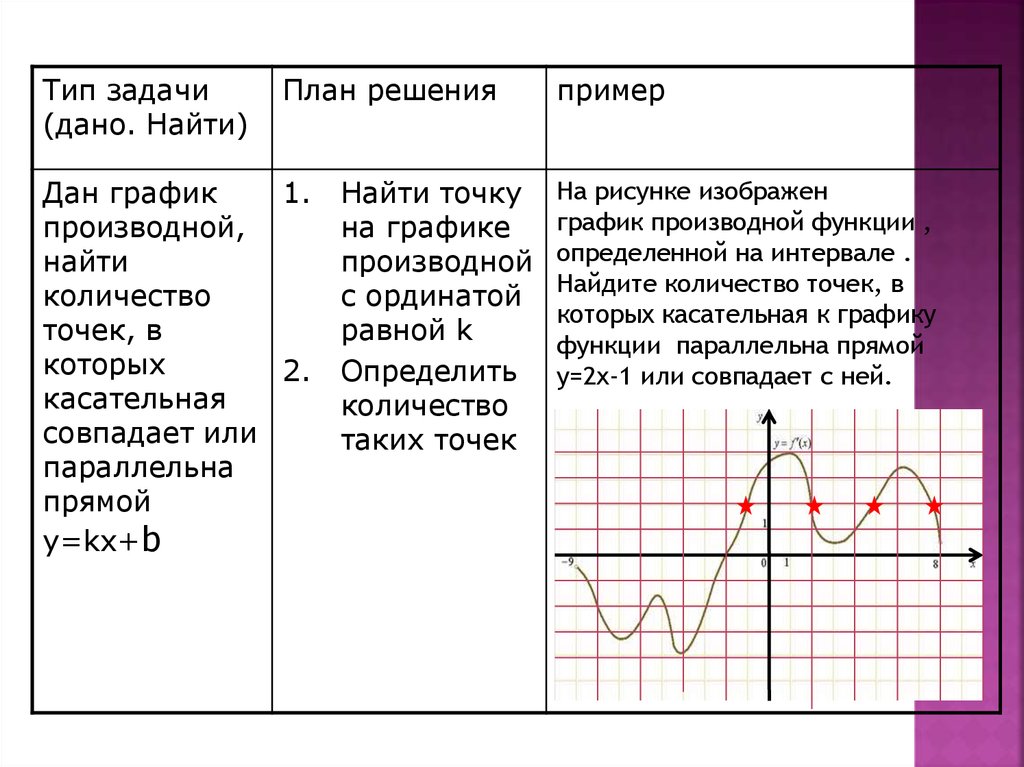
На рисунке изображен
график производной функции ,
определенной на интервале .
Найдите количество точек, в
которых касательная к графику
функции параллельна прямой
у=2х-1 или совпадает с ней.

3.

Тип задачи
(дано. Найти)
План решения
пример
Дан график
функции,
найти
количество
целых точек,
в которых
производная
функции отриц
ательна
(положительна)
определить
количество
целых
клеток в
промежутках
убывания
(возрастани
я)
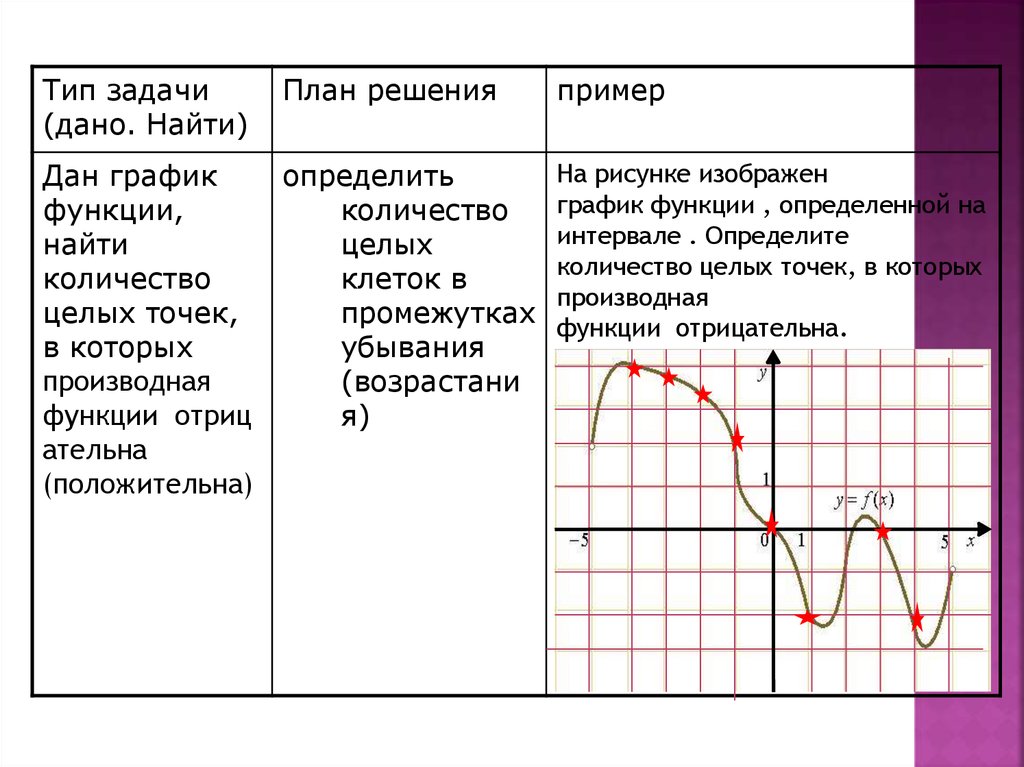
На рисунке изображен
график функции , определенной на
интервале . Определите
количество целых точек, в которых
производная
функции отрицательна.

4.

Тип задачи
(дано.
Найти)
План решения
Дан график определить
производной
количество
функции,
точек
найти
пересечения
количество
графика
точек
производной
экстремума
с осью ОХ
пример
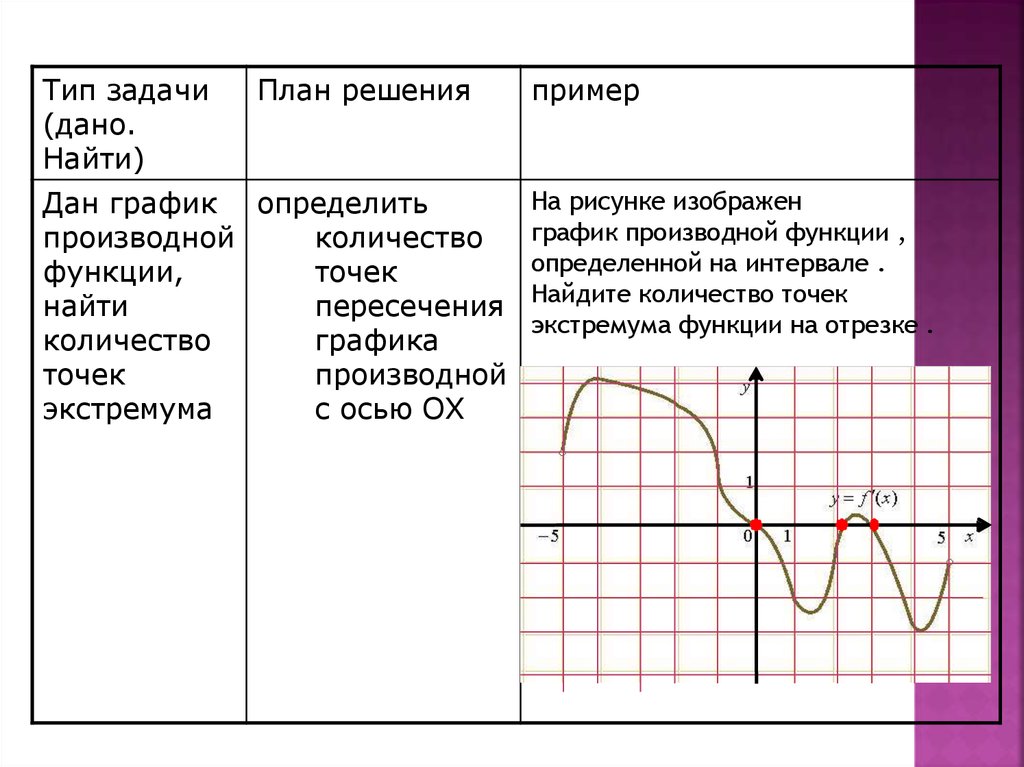
На рисунке изображен
график производной функции ,
определенной на интервале .
Найдите количество точек
экстремума функции на отрезке .

5.

Тип задачи
(дано.
Найти)
План решения
пример
Дан график
функции,
найти
значение
производной
функции в
точке .
1.Построить
треугольник,
в котором
касательная
является
гипотенузой
2.Найти тангенс
угла между
касательной
и осью ОХ
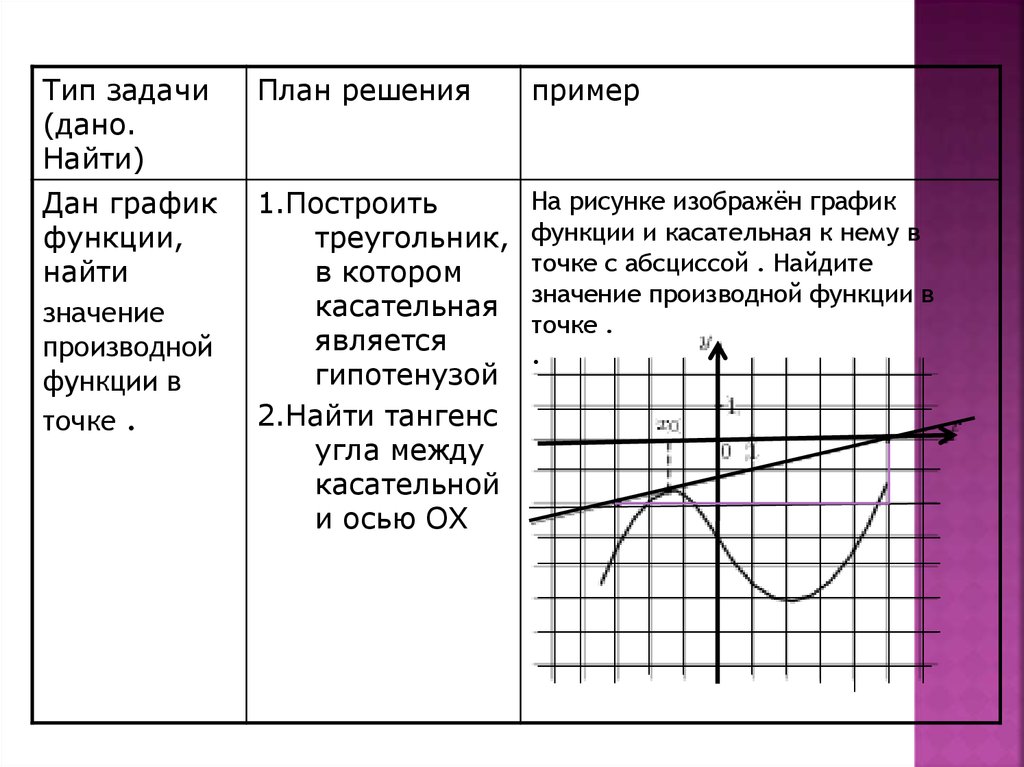
На рисунке изображён график
функции и касательная к нему в
точке с абсциссой . Найдите
значение производной функции в
точке .
.

6.

Тип задачи
(дано.
Найти)
План решения
пример
Прямая
параллельна
Дано
1.Найти
касательной к графику функции
уравнение
производную
касательной 2.Прировнять
. Найдите
к графику
производную к абсциссу точки касания.
функции и
коэффициенту
уравнение
k в уравнении
самой
касательной.
функции,
3.Решить
найти
уравнение
абсциссу
точки касания

7.

Тип задачи
(дано.
Найти)
План решения
На рисунке
Найти точку
изображен
пересечения
график
графика
производной
производной с
функции ,
осью абсцисс
определенной
на
интервале . В
какой точке
отрезка при
нимает
наибольшее
(наименьшее)
значение.
пример
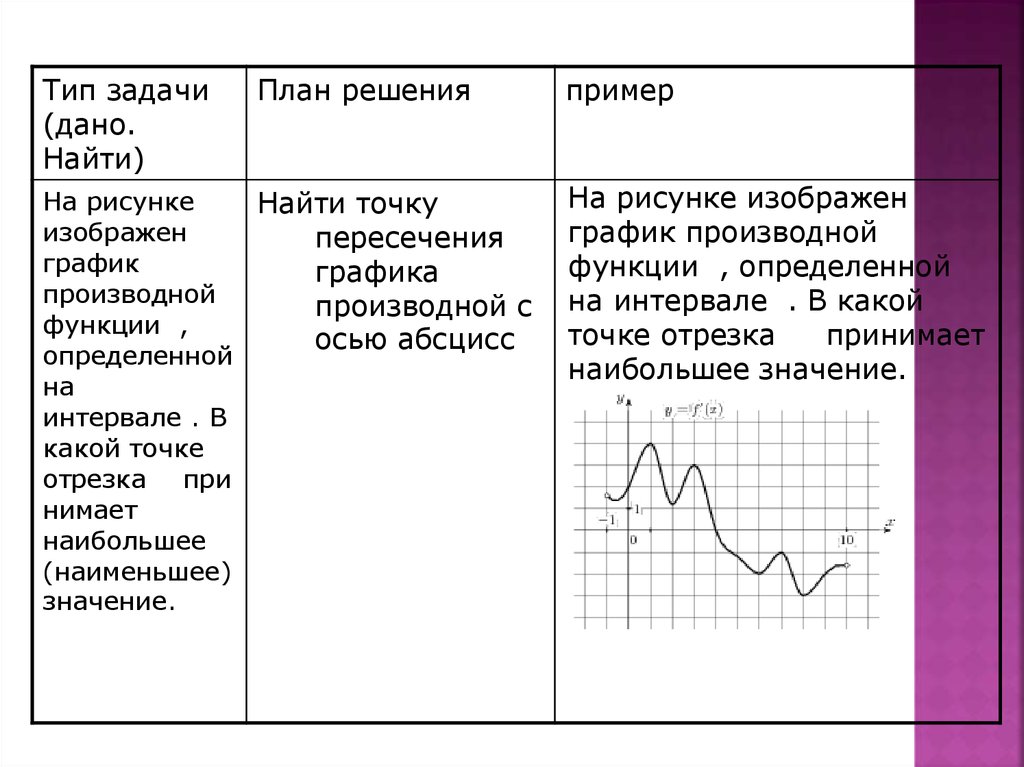
На рисунке изображен
график производной
функции , определенной
на интервале . В какой
точке отрезка
принимает
наибольшее значение.