Исследование функции на монотонность

1. Исследование функции на монотонность

ИССЛЕДОВАНИЕ ФУНКЦИИ НА
МОНОТОННОСТЬ

2.

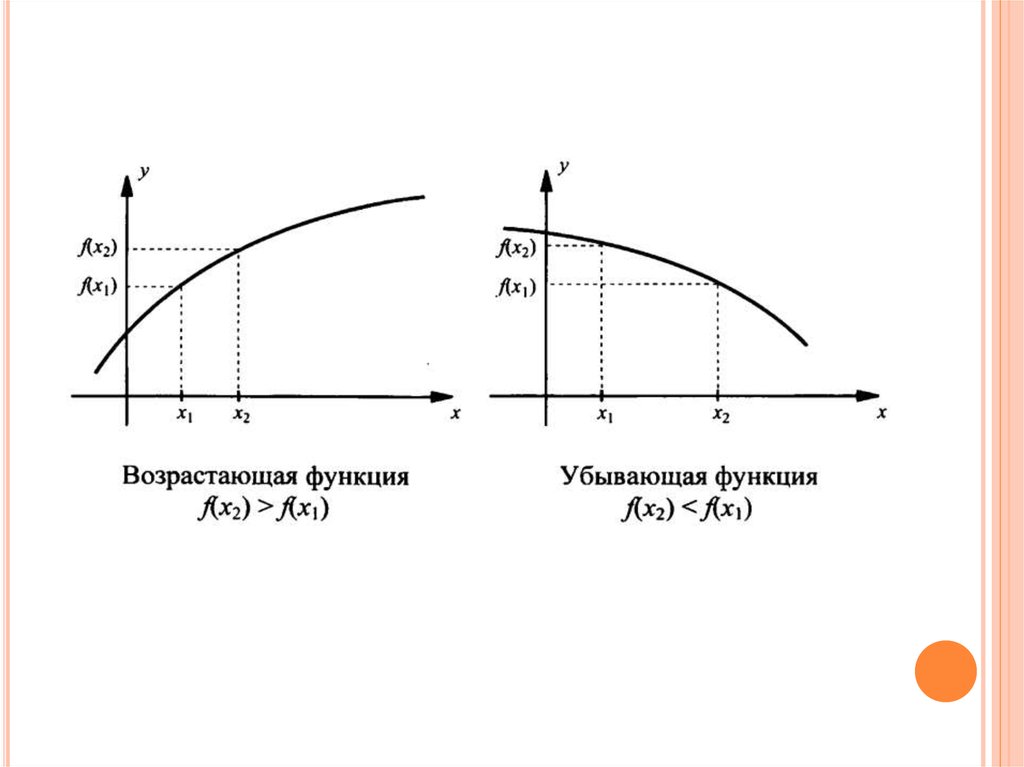
Определение 1.
Функцию у = f(x) называют возрастающей на промежутке X, если из
неравенства х1 < х2,где х1 и х2 — любые две точки промежутка X, следует
неравенство f(x1) < f(x2).
Функция возрастает, если большему значению аргумента соответствует
большее значение функции;
Определение 2.
Функцию у = f(x) называют убывающей на промежутке X, если из
неравенства х1 < х2, где х1 и х2 — любые две точки промежутка X,
следует неравенство f(x1) > f(x2).
функция убывает, если большему значению аргумента соответствует
меньшее значение функции.

3.

4.

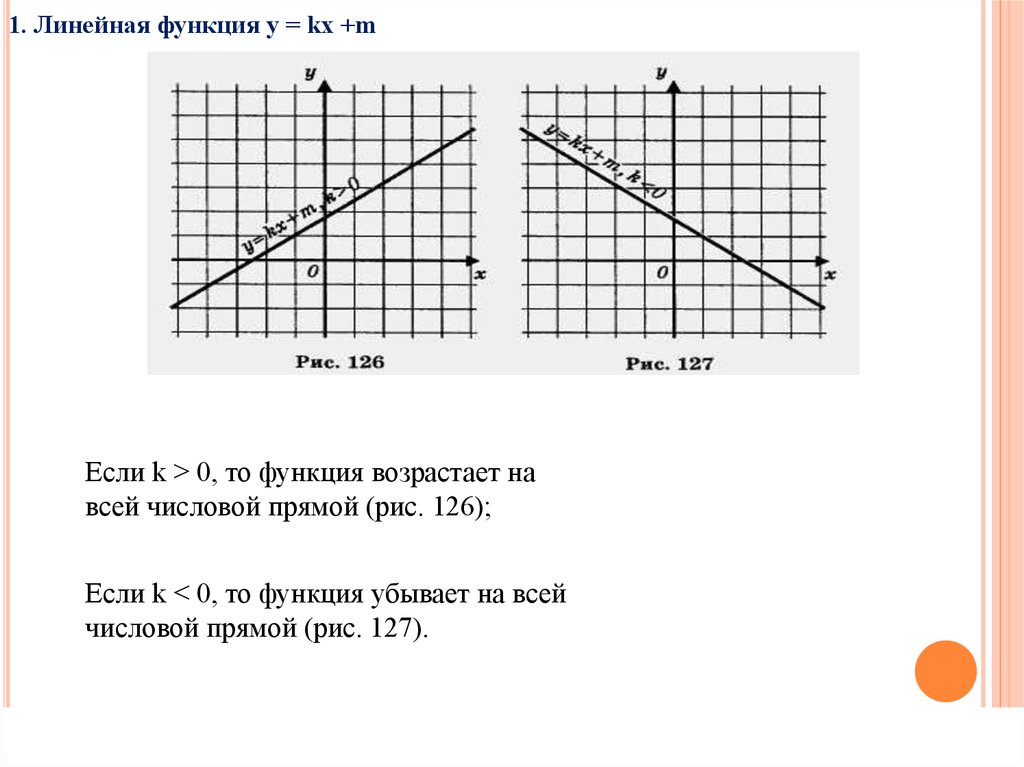
1. Линейная функция у = kx +m
Если k > 0, то функция возрастает на
всей числовой прямой (рис. 126);
Если k < 0, то функция убывает на всей
числовой прямой (рис. 127).

5.

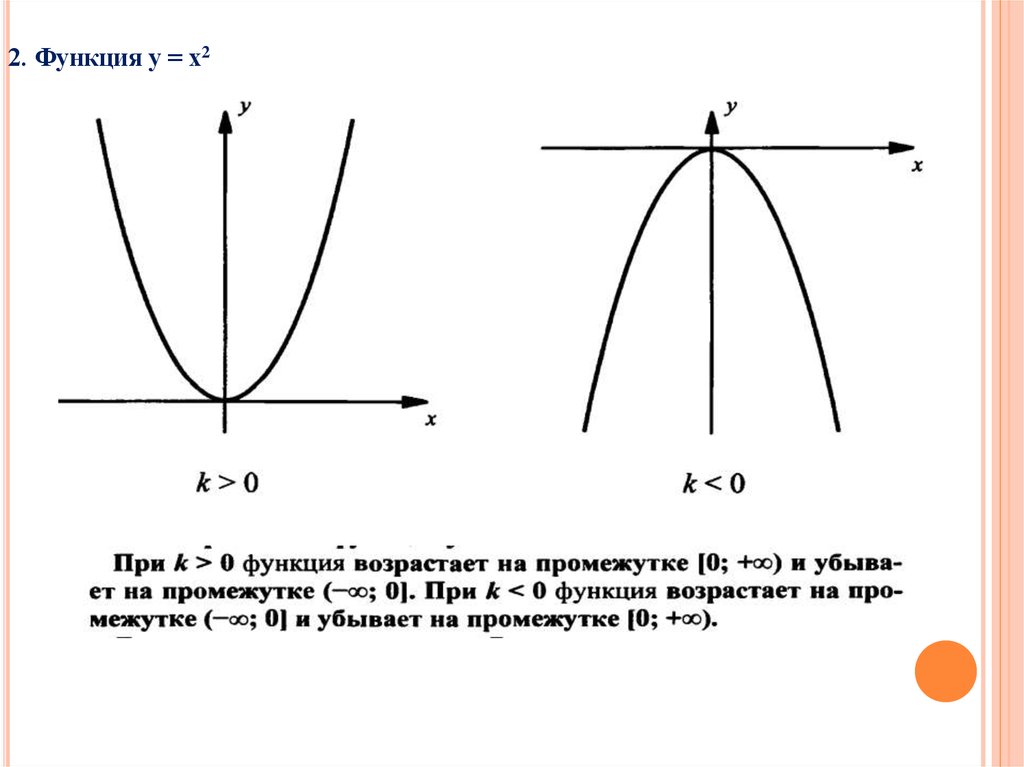
2. Функция у = х2

6.

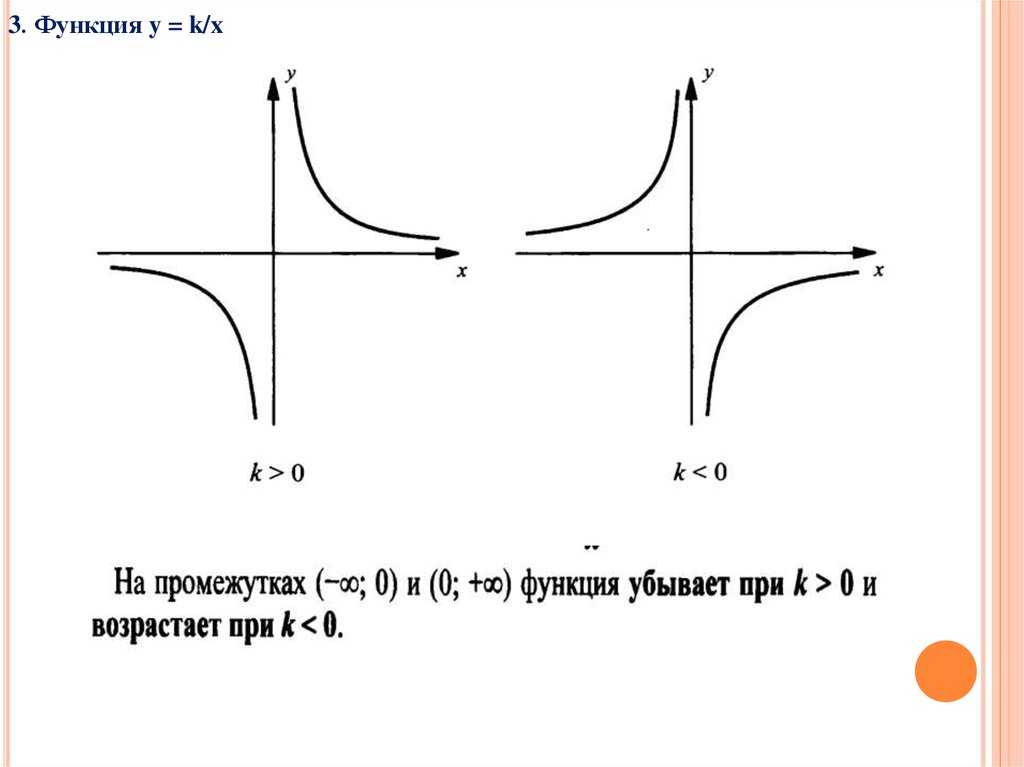
3. Функция y = k/x

7.

8. В классе:

В КЛАССЕ:
№ 1371-1375,
№ 1376(а,б)-1378(а,б)

9. Домашнее задание.

ДОМАШНЕЕ ЗАДАНИЕ.
Выучить конспект в тетради!!!!