Похожие презентации:
Размещения, сочетания, перестановки. 11 класс
1. Тема урока: «Размещения, сочетания, перестановки»
Урок алгебры в 11 классеУчитель: Хасаншина Р.Ш.
2.
•учебные заведения (составление расписаний);•сфера общественного питания (составление меню);
•лингвистика (рассмотрение вариантов комбинаций
букв).
3.
•география (раскраска карт);•спортивные соревнования (расчёт количества игр
между участниками);
•производство (распределение нескольких видов
работ между рабочими);
4.
•агротехника (размещение посевов на несколькихполях);
•азартные игры (подсчёт частоты выигрышей);
•химия (анализ возможных связей между
химическими элементами);
5.
•биология (расшифровка кода ДНК);•военное дело (расположение подразделений);
•астрология (анализ расположения планет и
созвездий);
6.
•экономика (анализ вариантов купли-продажиакций);
•криптография (разработка методов шифрования);
•доставка почты (рассмотрение вариантов пересылки).
7. Заполните пропуски:
1.
...!
A
(n k )!
2
.
n!
C
(... k )!...!
...
n
k
...
3
.
Pn ...!
8. Заполните пропуски:
4.
...!
A
(... 3)!
...
5
...!
5 С
(8 ...)!...!
.
2
...
6
.
Р... 3!
9. Проверь:
1.
n!
A
(n k )!
2
.
n!
C
(n k )! k!
k
n
k
n
3
.
Pn n!
10. Проверь:
4.
5!
A
(5 3)!
3
5
8!
5 С
(8 2)!2!
.
2
8
6
.
P3 3!
11. Прочитайте правильно:
1.
2
.
3
.
4
.
3
7
4
10
10
90
2
8
A , C , C , P12 , A
С , А , P90 , A , C
3
9
6
17
5
13
49
100
7
14
2
9
30
88
3
10
15
21
7
19
A , C , P14 , C , A
5
15
12
56
P20 , C , A , C , A
12. Типичные задачи, в которых обычно путаются учащиеся:
СочетанияРазмещения
1. Сколько рукопожатий
получится, если
здороваются 5 человек?
{Вася, Петя} = {Петя, Вася} –
одно и тоже.
Значит, порядок неважен,
значит это подмножество по
два элемента из 5, значит
это сочетание из пяти по
два.
2. Сколькими способами
пять человек
могут
т
обменяться фотографиями?
{Вася, Петя} ≠ {Петя, Вася} –
разные обмены.
Значит, порядок важен,
значит это
последовательность по два
элемента из 5, значит это
размещение из пяти по два.
13. Перестановки
1. Сколькими способами nчеловек могут сесть на
одной скамейке?
Pn = n!
2. Сколькими способами n
человек могут сесть за
круглым столом?
14.
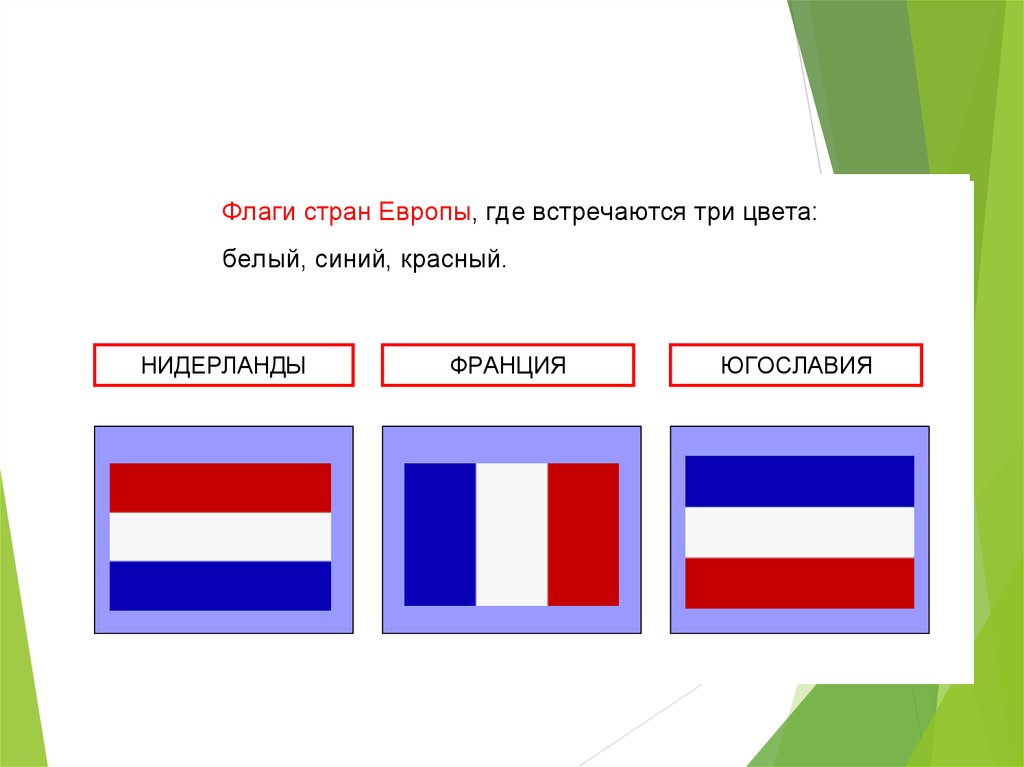
ФлагиФлаги стран
стран Европы,
Европы, где
где встречаются
встречаются три
три цвета:
цвета:
белый,
белый, синий,
синий, красный.
красный.
НИДЕРЛАНДЫ
НИДЕРЛАНДЫ
ФРАНЦИЯ
ФРАНЦИЯ
ЮГОСЛАВИЯ
ЮГОСЛАВИЯ
15.
Как подсчитать, сколько такихфлагов мы можем составить из
трех цветных полосок?
16.
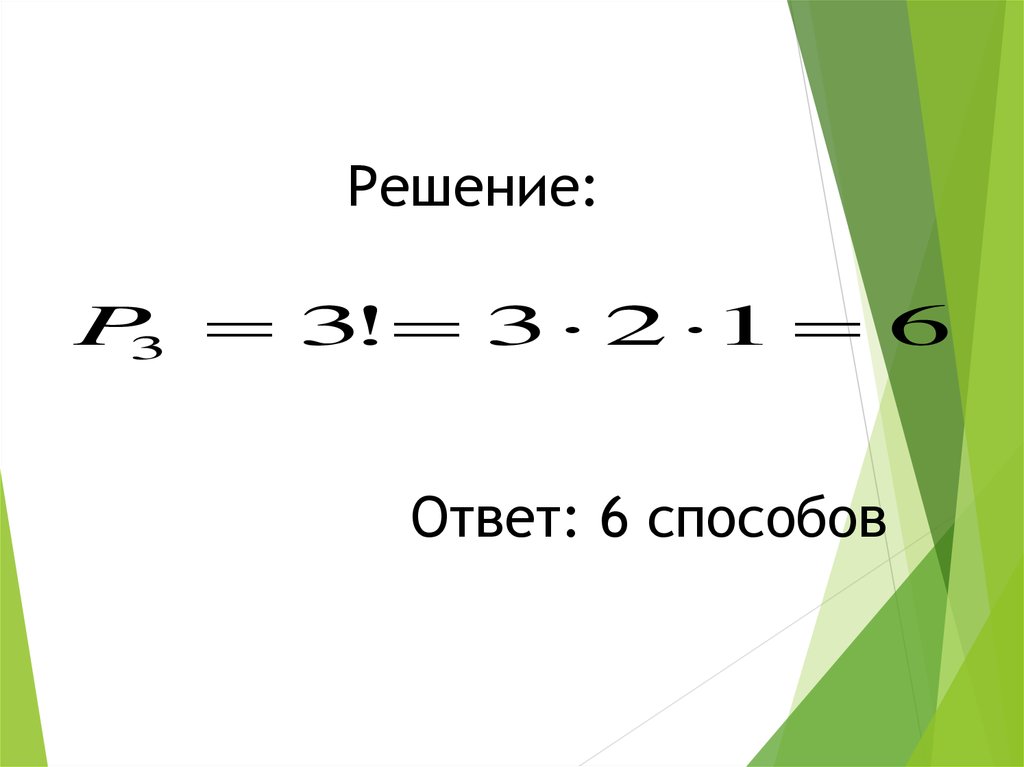
Решение:P3 3! 3 2 1 6
Ответ: 6 способов
17.
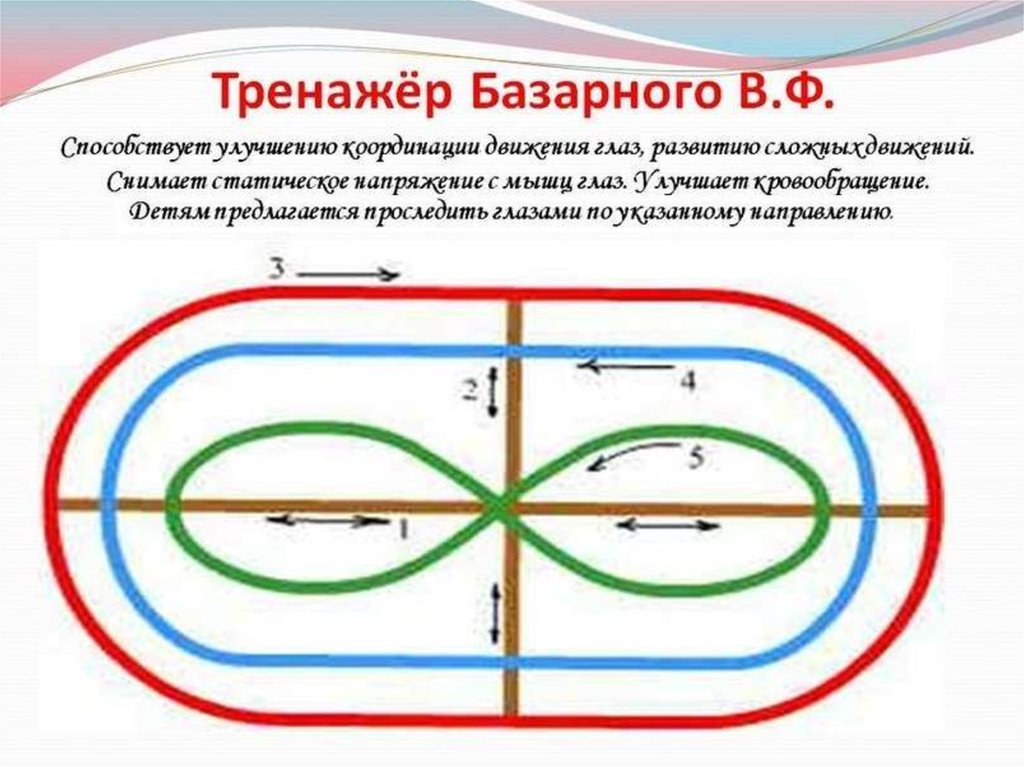
Всю неделю по - порядку,Глазки делают зарядку.
В понедельник, как проснутся,
Глазки солнцу улыбнутся,
Вниз посмотрят на траву
И обратно в высоту.
Во вторник часики глаза,
Водят взгляд туда – сюда,
Ходят влево, ходят вправо
Не устанут никогда.
В среду в жмурки мы играем,
Крепко глазки закрываем.
Раз, два, три, четыре, пять,
Будем глазки открывать.
Жмуримся и открываем
Так игру мы продолжаем.
По четвергам мы смотрим вдаль,
На это времени не жаль,
Что вблизи и что вдали
Глазки рассмотреть должны.
В пятницу мы не зевали
Глаза по кругу побежали.
Остановка, и опять
В другую сторону бежать.
Хоть в субботу выходной,
Мы не ленимся с тобой.
Ищем взглядом уголки,
Чтобы бегали зрачки.
В воскресенье будем спать,
А потом пойдём гулять,
Чтобы глазки закалялись
Нужно воздухом дышать.
Без гимнастики, друзья,
Нашим глазкам жить нельзя!
18. Задача 1.
7 февраля в расписании Олимпийских игр былизаявлены следующие виды спорта: биатлон,
конькобежный спорт, лыжные гонки и сноуборд.
Сколькими способами можно составить
расписание из данных видов спорта на 7 февраля?
Сколькими способами можно составить
расписание, если известно, что биатлон должен
идти первым?
19.
Решение:1)4! 4 3 2 1 24
2)3! 3 2 1 6
Ответ: 24 способа и 6 способов.
20. Задача 2.
Среди наиболее популярныхталисманов Олимпиады в составе
Белого Медведя, Деда Мороза,
Снежного Барса, Зайца, Лучика и
Снежинки выбирали 3-х
финалистов. Сколько
всевозможных троек финалистов
можно составить?
21.
Решение:6!
6 5 4 3 2 1
С
(6 3)!3! 3 2 1 3 2 1
3
6
4 5 20
Ответ: 20 троек.
22. Задача 3.
Для конькобежного спортаотведено 5 дорожек. Сколькими
способами можно расставить на
них 5 спортсменов? 3
спортсмена?
23.
Решение:1) А 5! 5 4 3 2 1 120
5
5
5!
5 4 3 2 1
2) A
60
(5 3)!
2 1
3
5
Ответ: 120 и 60 способов.
24. Задача 4.
9 команд по хоккею участвуют втурнире. Каждая команда
провела с каждой из остальных
по одной игре. Сколько всего
игр было сыграно?
25.
Решение:9!
7! 8 9
С
36
(9 2)!2! 7! 1 2
2
9
Ответ: 36 игр.
26. Тест по комбинаторике
Вариант 1.1. Сколькими способами можно составить расписание одного
учебного дня из 5 различных уроков?
1) 30 2) 100 3) 120 4) 5 взаимопроверка)
2. В 9«Б» классе 12 учащихся. Сколькими способами можно
сформировать команду из 4 человек для участия в математической
олимпиаде?
1) 128 2) 495 3) 36 4) 48
3. Сколько существует различных двузначных чисел, в записи
которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в
числе должны быть различными?
1) 10 2) 60 3) 20 4) 30
№ задания 1 2 3
№ ответа 3 2 4
27. Тест по комбинаторике
Вариант 2.1. Сколько различных пятизначных чисел можно составить из
цифр 1, 2, 3, 4, 5?
1) 100 2) 30 3) 5 4) 120
2. Имеются помидоры, огурцы, лук. Сколько различных салатов
можно приготовить, если в каждый салат должно входить 2
различных вида овощей?
1) 3 2) 6 3) 2 4) 1
3. Сколькими способами из 8 учебных предметов можно
составить расписание учебного дня из 4 различных уроков.
1) 10000 2) 1680 3) 32 4) 1600
№ задания 1 2 3
№ ответа 4 1 2







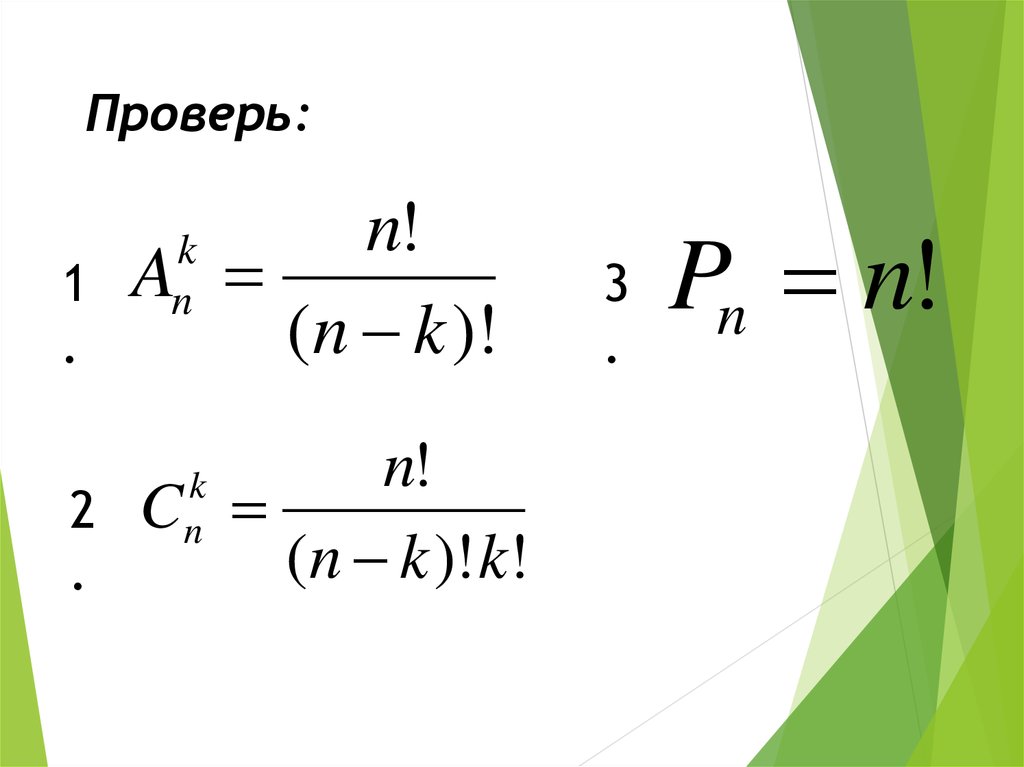
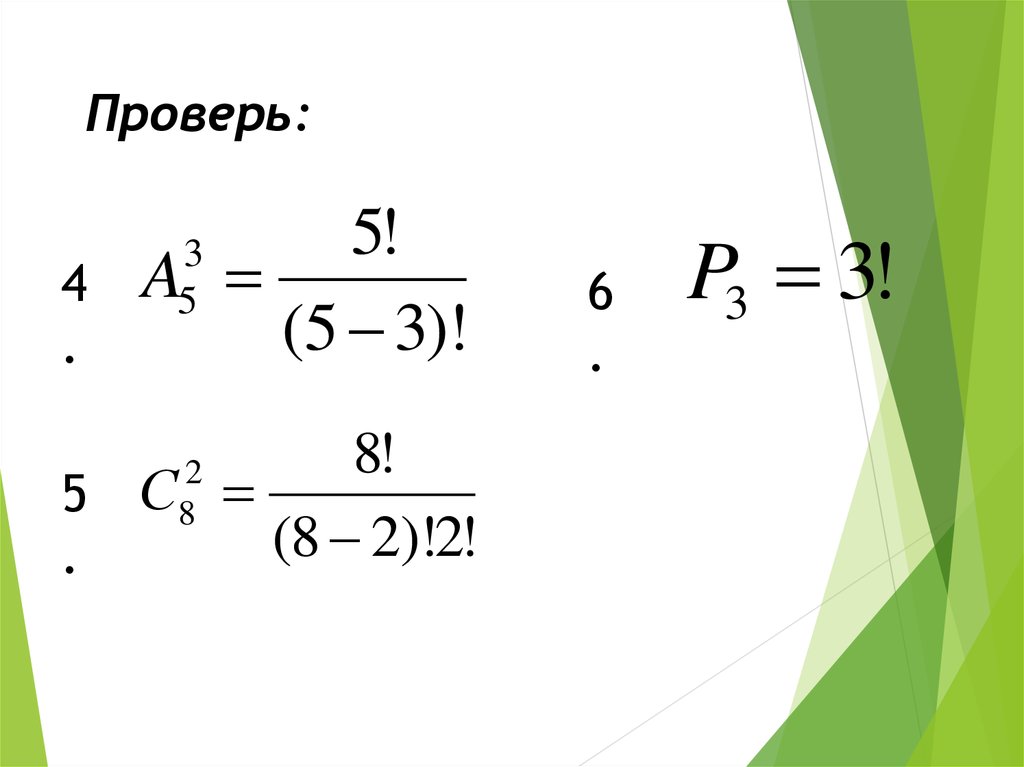















 Математика
Математика








