Методы решения тригонометрических уравнений

1. Обобщающий урок по теме: «Методы решения тригонометрических уравнений» 10 класс

Горбунова Вера
Александровна, учитель
физики и математики
МБОУ Черемуховская
СОШ Новошешминского
муниципального района РТ

2.

«Считай несчастным тот день
или тот час, в который ты не
усвоил ничего нового и ничего не
прибавил к своему образованию»
Я. А. Коменский

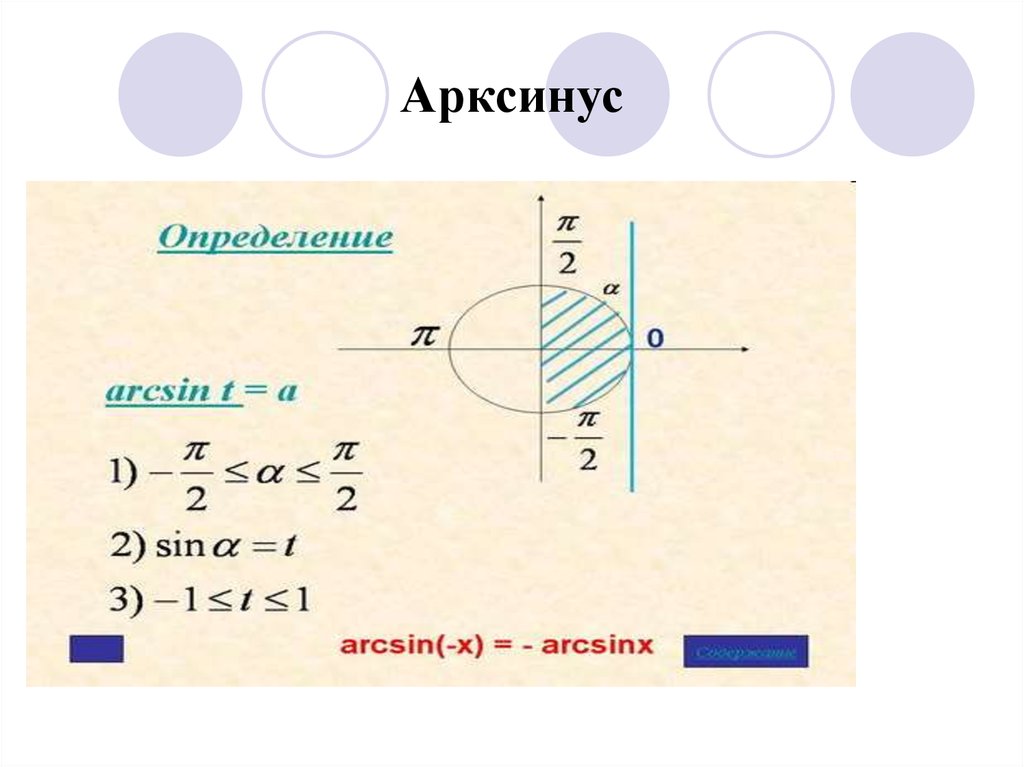
3. Арксинус

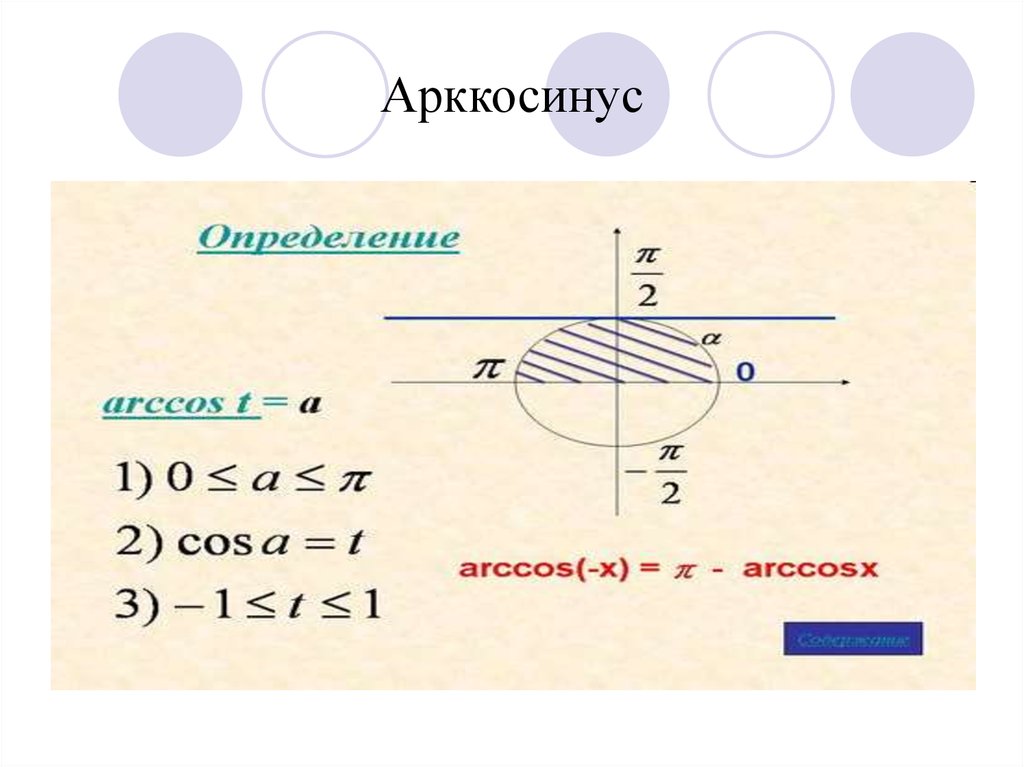
4. Арккосинус

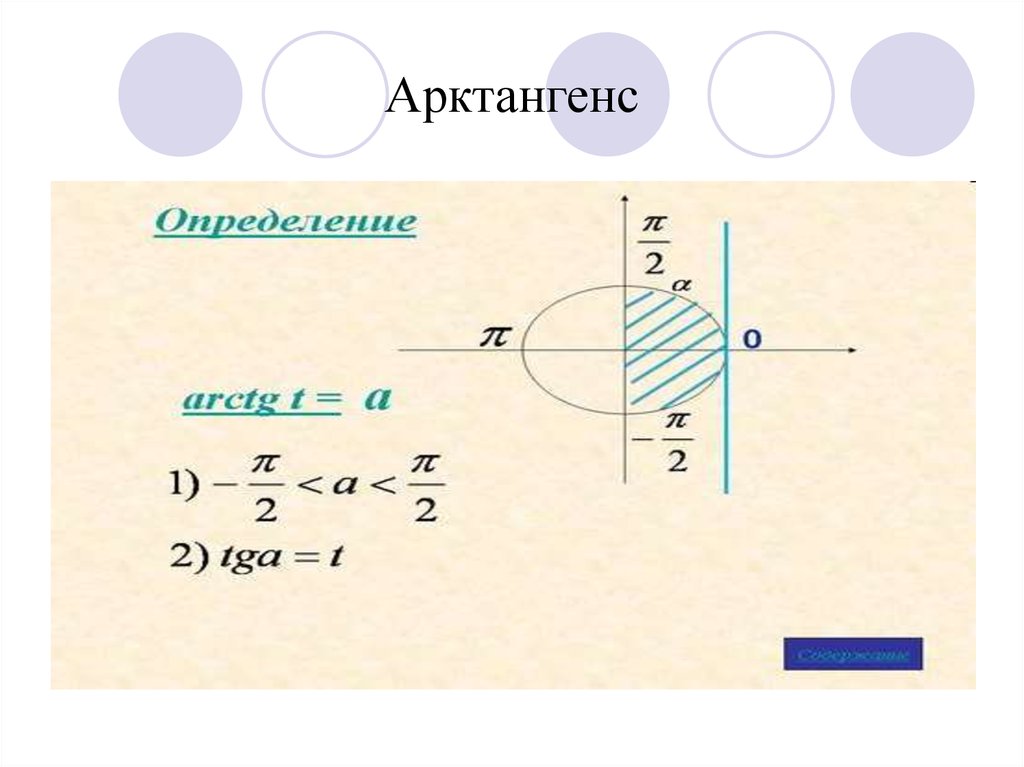
5. Арктангенс

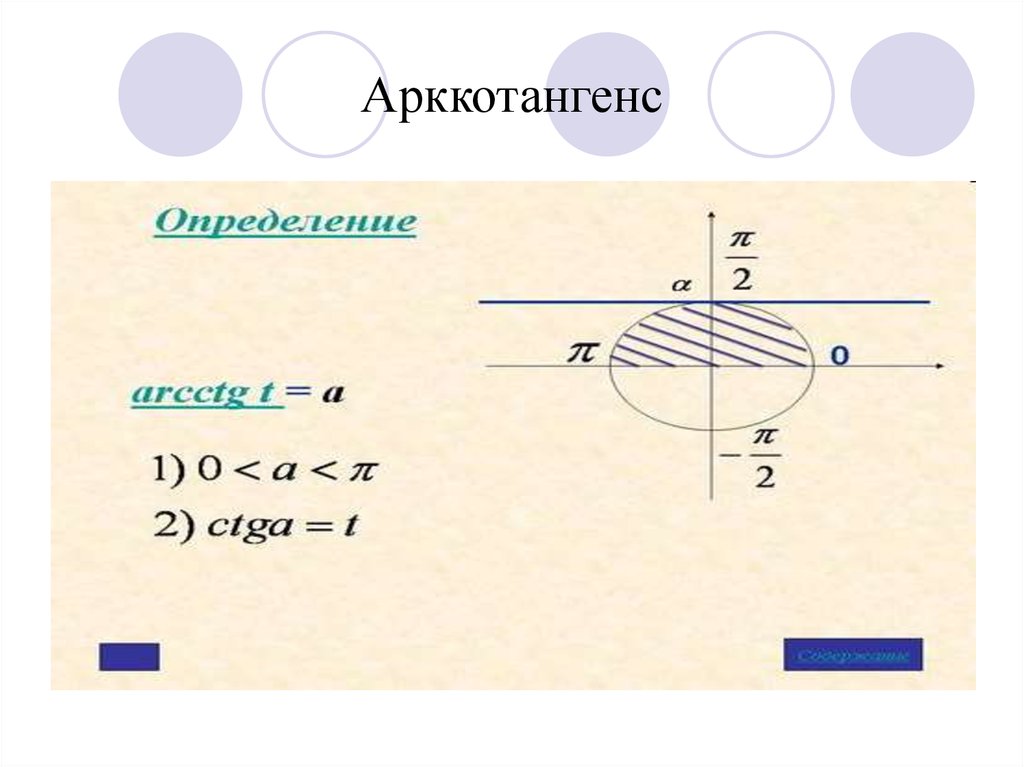
6. Арккотангенс

7. Финк- Райт – Раунд - Робин

arcsin √2/2
arccos 1
arcsin (- 1/2 )
arccos (- √3/2)
arctg √3

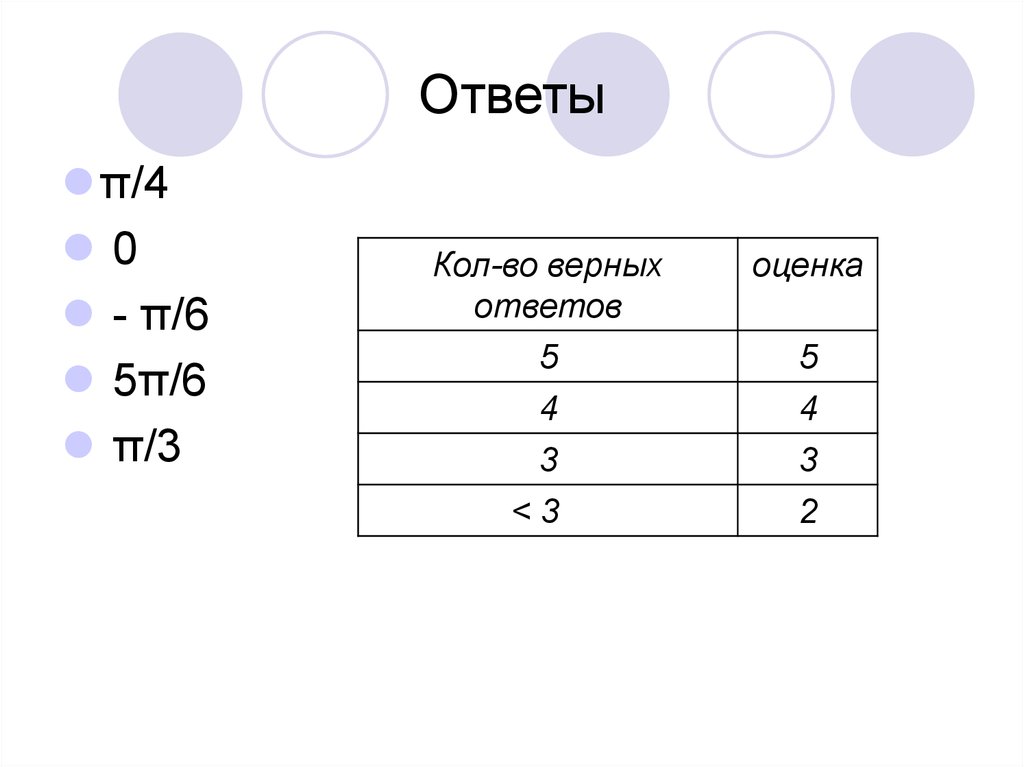
8. Ответы

π/4
0
- π/6
5π/6
π/3
Кол-во верных
ответов
5
4
3
<3
оценка
5
4
3
2

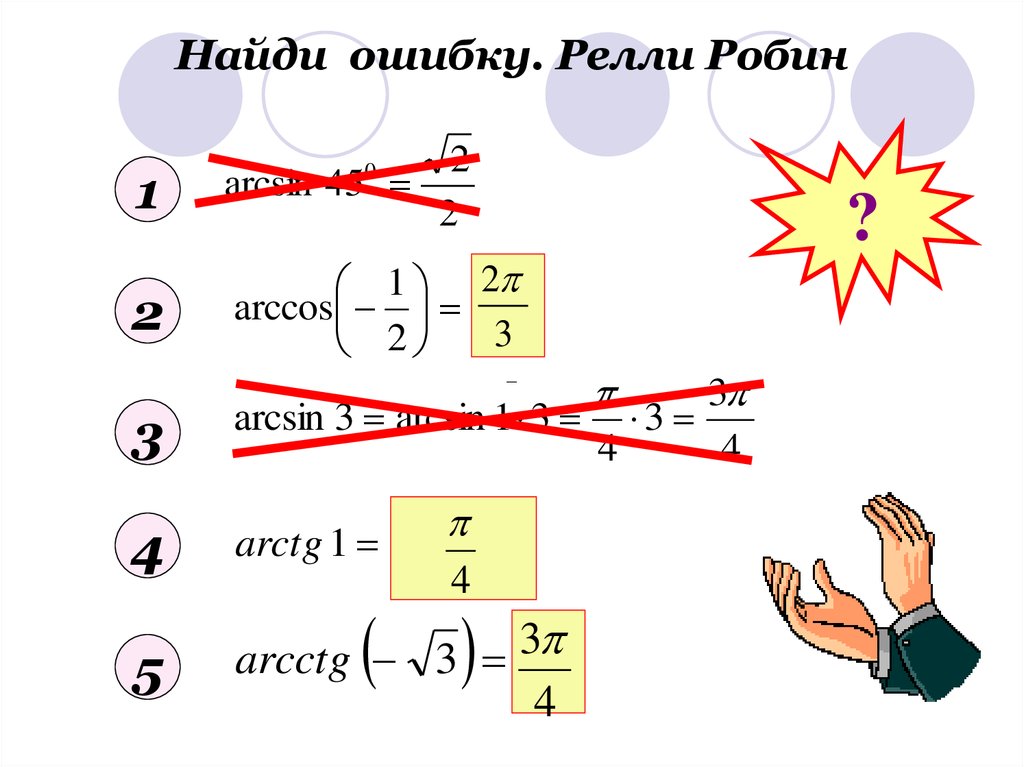
9. Найди ошибку. Релли Робин

1
2
arcsin 45
2
2
1 2
arccos
33
2
0
?
3
3
arcsin 3 arcsin 1 3 3
4
4
4
arctg 1 arctg
4 4
5
3
arcctg 3
46

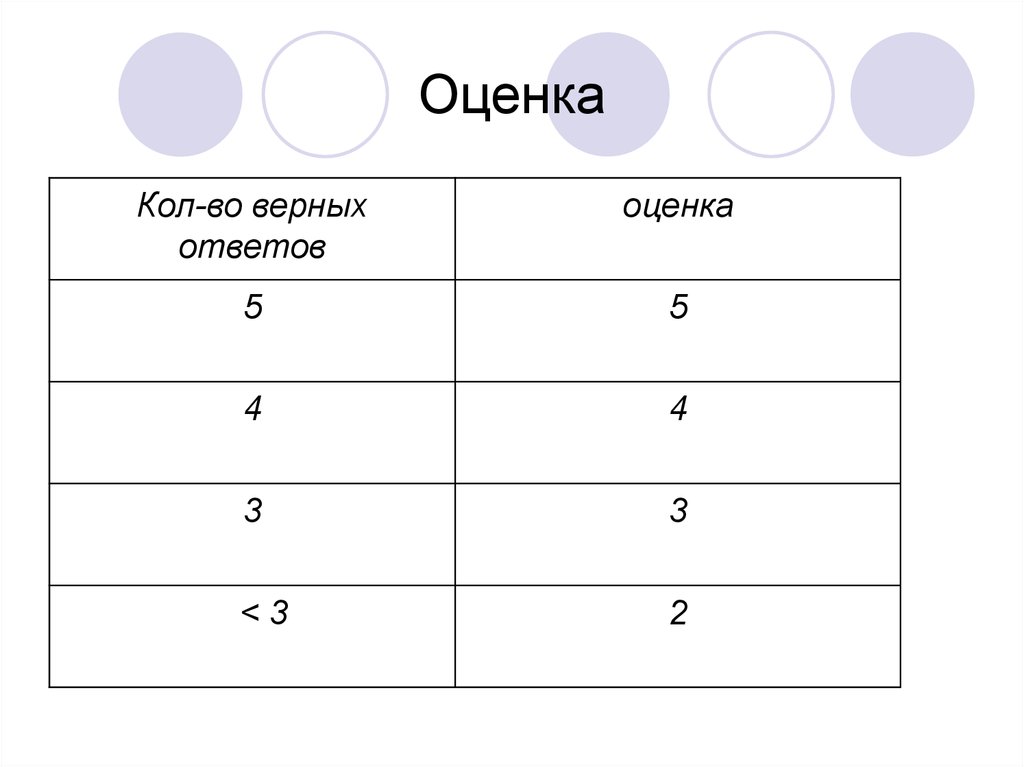
10. Оценка

Кол-во верных
ответов
оценка
5
5
4
4
3
3
<3
2

11.

Общая схема исследования функции
1. Область определения функции.
2. Исследование области значений функции
3. Исследование функции на четность.
4.. Исследование функции на периодичность
5. Формулы корней тригонометрических уравнений.

12. Функция у = sin x.

1. Областью определения функции является множество
всех действительных чисел ( R )
2. Областью значений) - [ - 1; 1 ].
3. Функция у = sin α нечетная, т.к. sin (- α) = - sin α
4. Функция периодическая, с главным периодом 2π
sint = а, где | а |≤ 1
1)sint=0
t = 0+πk‚ kЄZ
2)sint=1
t = π/2+2πk‚ kЄZ
3)sint = - 1
t = - π/2+2πk‚ kЄZ

13. Функция у = соs x.

1. Областью определения функции является множество
всех действительных чисел ( R )
2. Областью изменений (Областью значений) - [ - 1; 1 ]
3. Функция у = cos α четная, т.к. cos (- α) = cos α
4. Функция периодическая, с главным периодом 2π.
cost = а , где |а| ≤ 1
1)cost=0
t = π/2+πk‚ kЄZ
2)cost=1
t = 0+2πk‚ kЄZ
3)cost = -1
t = π+2πk‚ kЄZ

14. Функция у = tg x

1. Областью определения функции является
множество (- π/2; π/2)
2. Областью значений R.
3.Функция у = tg x нечетная, т.к. tg (- α) = - tg α
4. Функция периодическая, с главным
периодом π.
tgt = а, аЄR
t = arctg а + πk‚ kЄZ

15. Функция у = ctg x

1. Областью определения функции является
множество (πn; π + πn)
2. Областью значений R
3. Функция у = ctg x нечетная, т.к. ctg (- α) = - ctg α
4. Функция периодическая, с главным периодом π.
ctgt = а, аЄR
t = arcctg а + πk‚ kЄZ

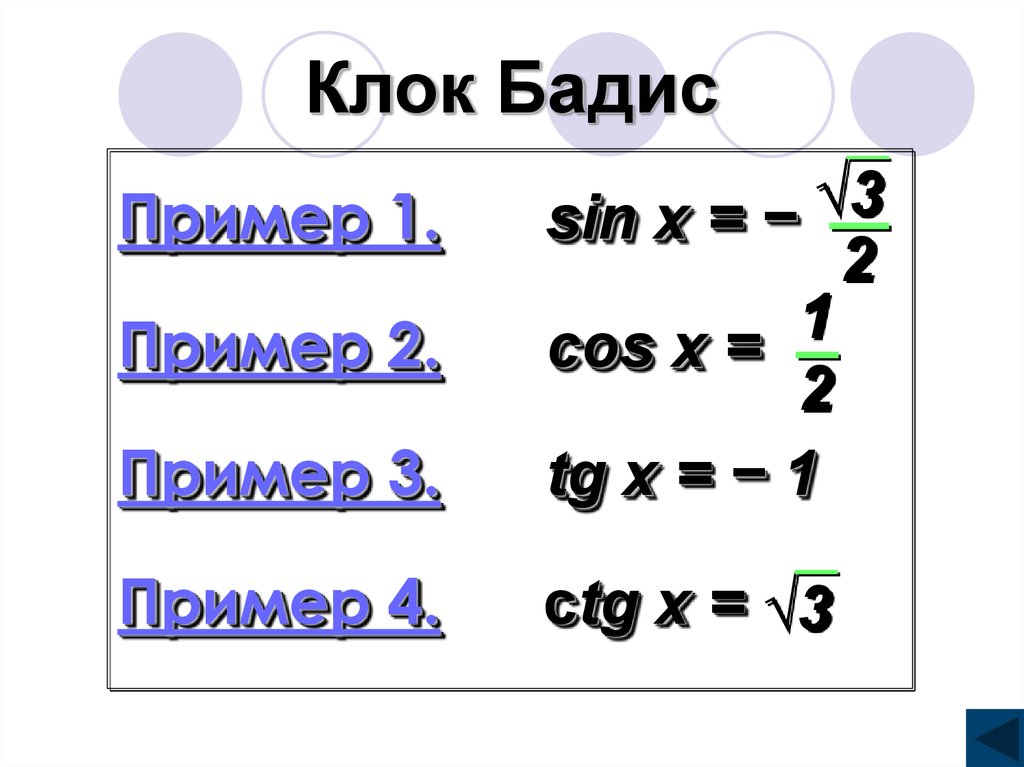
16. Клок Бадис

Пример 3.
√3
sin x = −
2
1
cos x =
2
tg x = − 1
Пример 4.
ctg x = √3
Пример 1.
Пример 2.

17.

√3
Пример 1 sin x = − 2
√3
x=
arcsin −
+ πn, n Z
2
√3
n+1
x = (−1) arcsin
+ πn, n Z
2
π
n+1
x = (−1)
+ πn, n Z
3
π
n+1
Ответ: (−1)
+ πn, n Z
3
(−1)n

18.

1
Пример 2 cos x =
2
1
x =+
arccos
+
2πn,
n Z
−
2
π
x=+
+
2πn,
n Z
−3
Ответ:
π
+ + 2πn, n Z
−3

19. Пример 3 tg x = − 1

x = arctg (− 1) + πn, n Z
x = − arctg 1 + πn, n Z
π
x = − + πn, n Z
4
π
Ответ: − 4 + πn, n Z

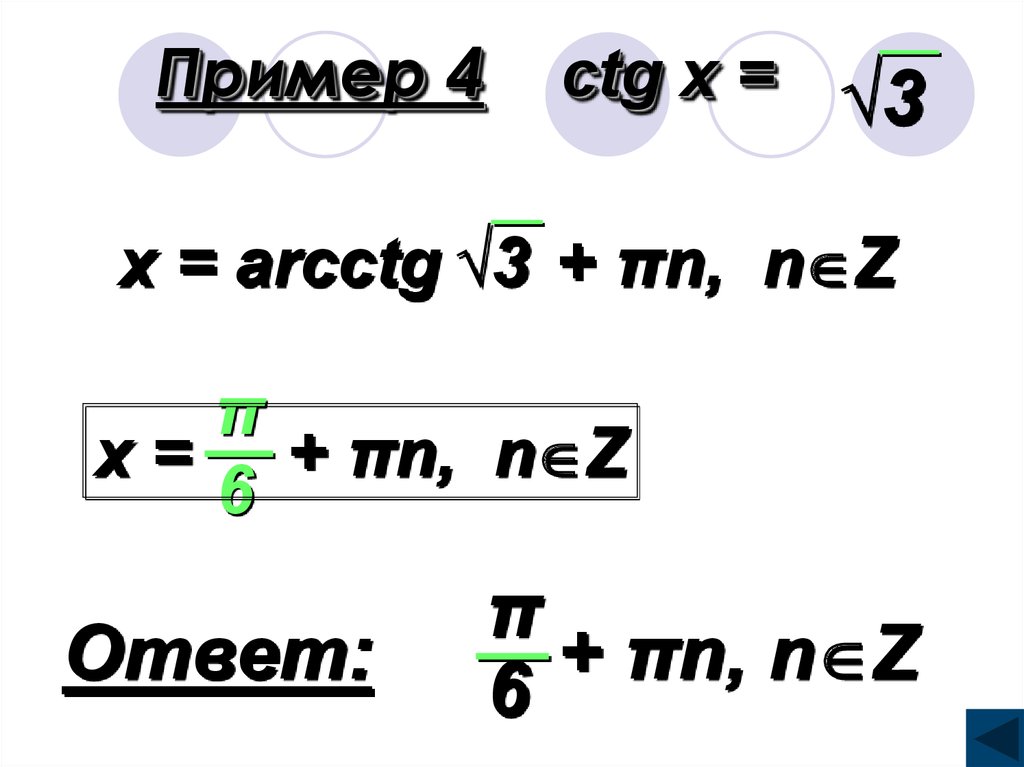
20. Пример 4 сtg x =

√3
x = arсctg √3 + πn, n Z
π
x = + πn, n Z
6
Ответ:
π
+
πn,
n Z
6

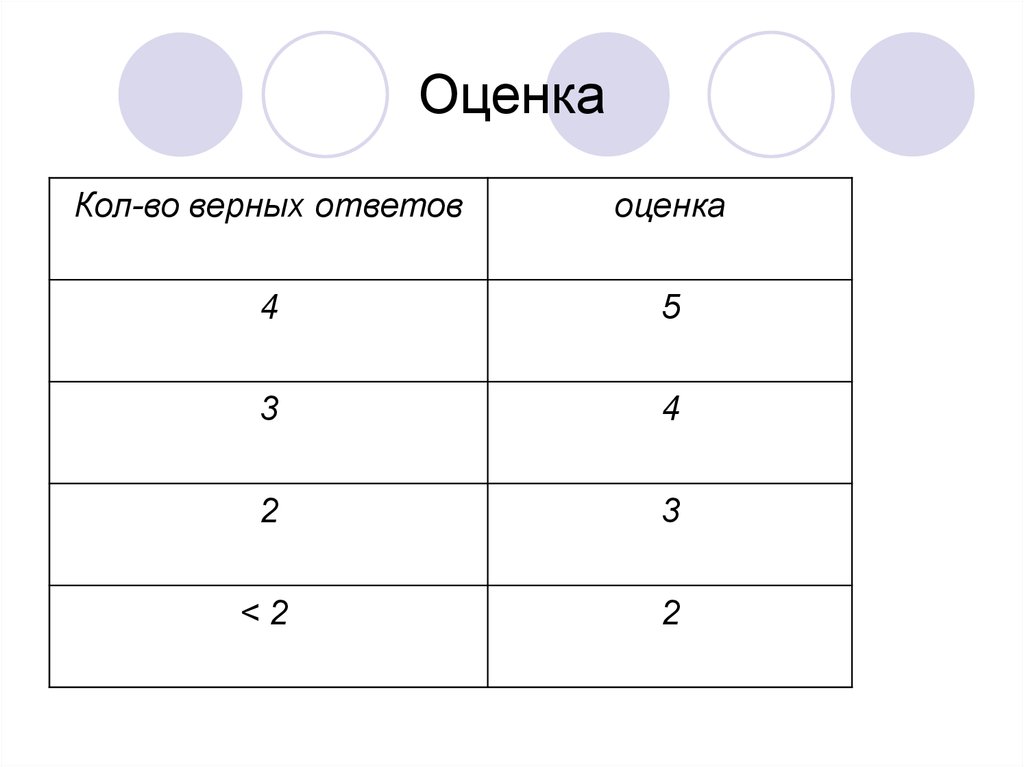
21. Оценка

Кол-во верных ответов
оценка
4
5
3
4
2
3
<2
2

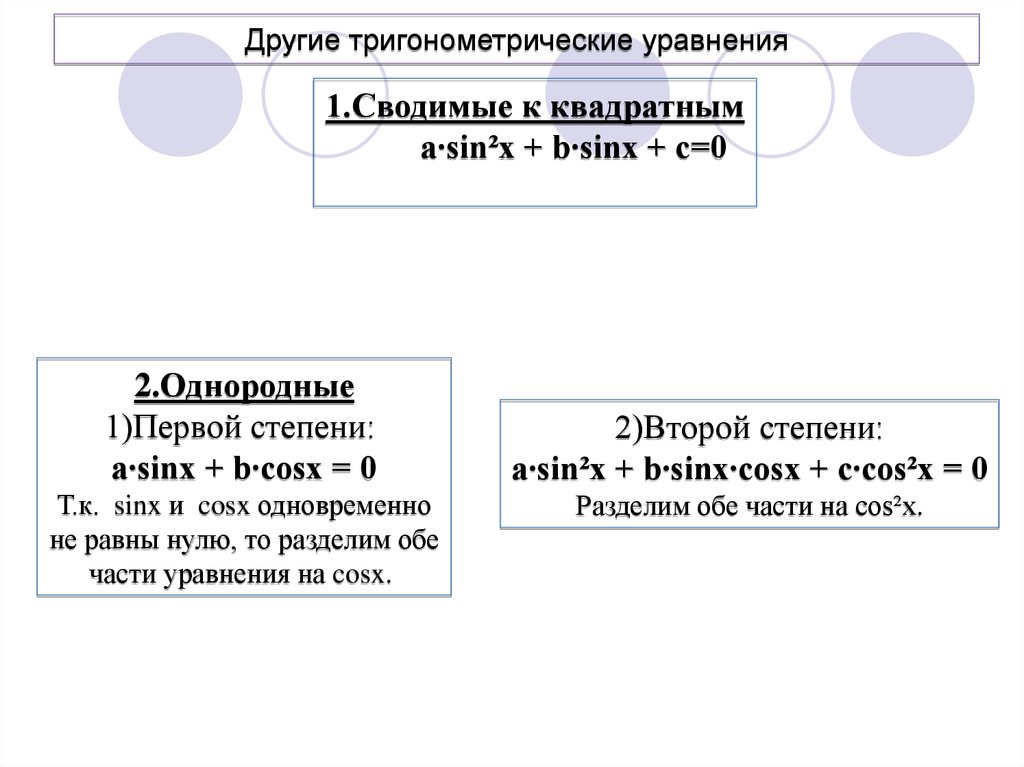
22. Другие тригонометрические уравнения

1.Сводимые к квадратным
a∙sin²x + b∙sinx + c=0
2.Однородные
1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно
не равны нулю, то разделим обе
части уравнения на cosx.
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x.

23. Содержание

Метод замены переменной
Метод разложения на множители
С помощью тригонометрических
формул:
− Формул сложения
− Формул приведения
− Формул двойного аргумента

24. Основные методы решения тригонометрических уравнений. Домашнее задание.

На «3»
1) 3 sin x+ 5 cos x = 0
2) 5 sin2 х - 3 sinх cos х 2 cos2х =0
На «4»
1) 3 cos2х + 2 sin х cos х
=0
2) 5 sin2 х + 2 sinх cos х cos2х =1
На «5»
1) 2 sin x - 5 cos x = 3
2) 1- 4 sin 2x + 6 cos2х =
На «3»
1) cos x+ 3 sin x = 0
2) 6 sin2 х - 5 sinх cos х +
cos2х =0
На «4»
1) 2 sin2 x – sin x cosx =0
2) 4 sin2 х - 2sinх cos х –
4 cos2х =1
На «5»
1) 2 sin x - 3 cos x = 4
2) 2 sin2 х - 2sin 2х +1 =0

25. « То, что мы знаем, - ограниченно, а то чего мы не знаем, - бесконечно». Пьер Лаплас:

« То, что мы знаем, ограниченно, а то чего мы
не знаем, - бесконечно».
Пьер Лаплас:

26.

27. Билетик на выход

а)2
2
cos х
+ 5 sin х - 4=0
б)3 sin x - 2 cos2x =0