Квадратные уравнения. Из истории

1. Квадратные уравнения

ГБОУ СОШ № 249
Теплякова Людмила Федоровна

2. Из истории

В Древней Индии
были распространены
публичные соревнования в
решении трудных задач. В одной
из старинных индийских книг
говорится по поводу таких
соревнований следующее: «Как
солнце блеском своим
затмевает звезды, так ученый
человек затмит славу другого в
народных собраниях, предлагая
и решая алгебраические
задачи».

3. Основные понятия

Квадратным уравнением называют уравнения
вида ax²+bx+c = 0, где коэффициенты a, b, c–
любые действительные числа, причём a ≠ 0.
Квадратное уравнение называют приведённым,
если его старший коэффициент равен 1.

4. Способы решения 1. Формулы

Подкоренное выражение b²-4ac называется
дискриминантом
D= b²-4ac
при D>0 два кореня ;
при D=0 один корень (в некоторых контекстах
говорят также о двух равных или совпадающих
корнях);
при D<0 корней на множестве действительных чисел
нет.

5. Корни квадратного уравнения при чётном коэффициенте b

Все необходимые свойства при этом
сохраняются:

6. Неполные квадратные уравнения

b = 0; c = 0
b = 0; c ≠ 0
b ≠ 0; c = 0
или

7. Свойства коэффициентов квадратного уравнения

ax²+bx+c = 0
Если a+c=b, то
c
х1 1; x2
a
c
х1 1; x2
a
Если a+c+b=0, то

8. 2. Разложение левой части уравнения на множители.

х² + 10х - 24 = 0
х² + 10х - 24 = х² + 12х - 2х - 24 = х(х + 12)
- 2(х + 12) = (х + 12)(х - 2).
(х + 12)(х - 2) = 0
х = 2, х = - 12.

9. 3. Метод выделения полного квадрата.

х² + 6х - 7 = 0
х² + 6х - 7 = х² + 6х + 9 - 9-7=(х² + 6х + 9)16 = (х+3)²-16
(х+3)²-16 =0
(х+3)²=16
х+3=4 или х+3=-4
х = 1, или х = -7.

10. Решение уравнений с использованием теоремы Виета

x²+ px + q = 0
x1 + x2 = - p
x1.x2 = q

11. Решение уравнений способом переброски

Рассмотрим квадратное уравнение
ах² + bх + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем
уравнение
а²х² + ах + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к
уравнению
у² + by + ас = 0,
равносильно данному. Его корни у1и у2
найдем с помощью теоремы Виета.
Окончательно получаем
х1 = у1/а и х1 = у2/а.

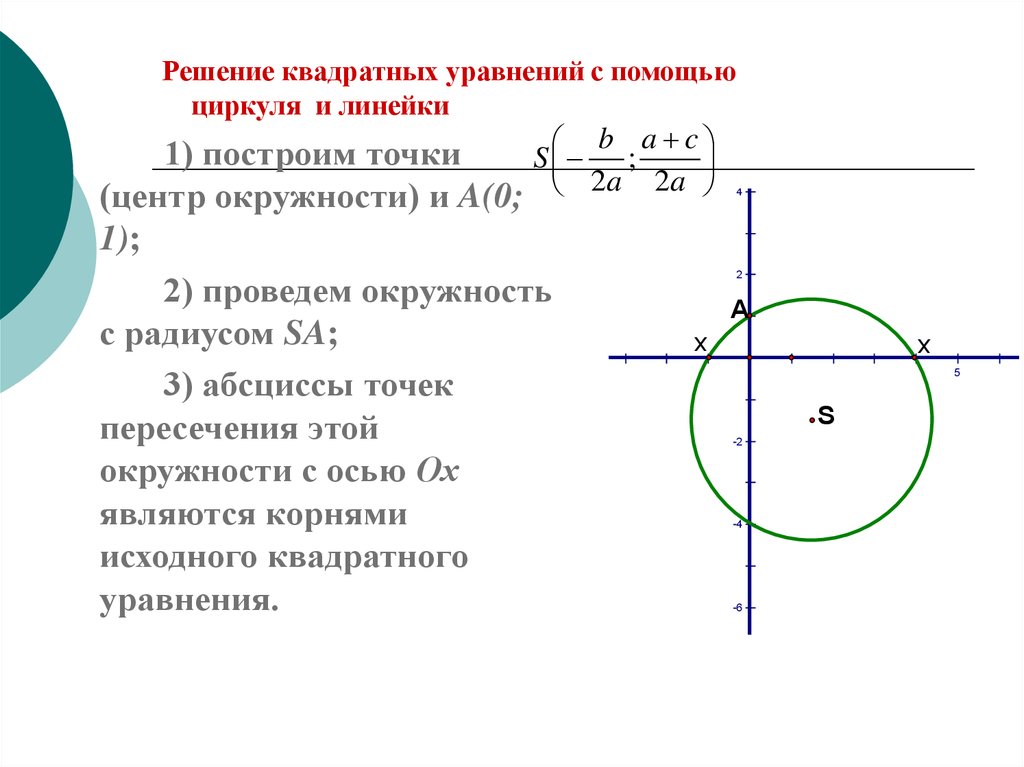
12. Решение квадратных уравнений с помощью циркуля и линейки

b a c
1) построим точки
S ;
2
a
2
a
(центр окружности) и A(0;
1);
2) проведем окружность
с радиусом SA;
х
3) абсциссы точек
пересечения этой
окружности с осью Ох
являются корнями
исходного квадратного
уравнения.
6
4
2
А
х
-5
5
S
-2
-4
-6
-8

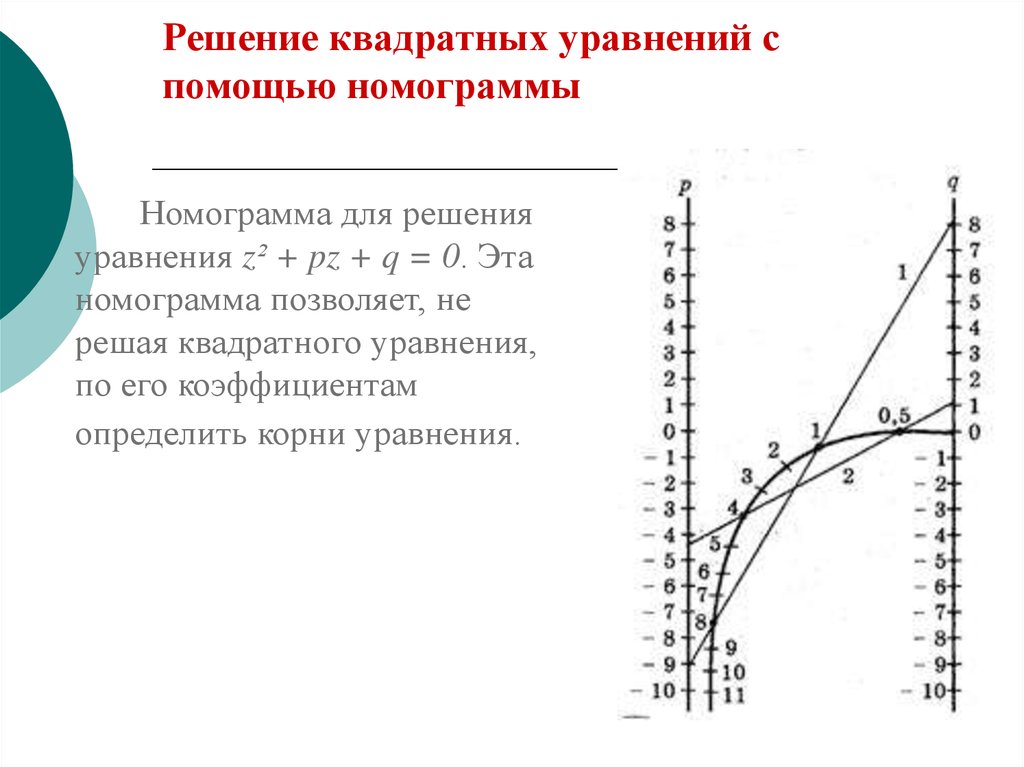
13. Решение квадратных уравнений с помощью номограммы

Номограмма для решения
уравнения z² + pz + q = 0. Эта
номограмма позволяет, не
решая квадратного уравнения,
по его коэффициентам
определить корни уравнения.

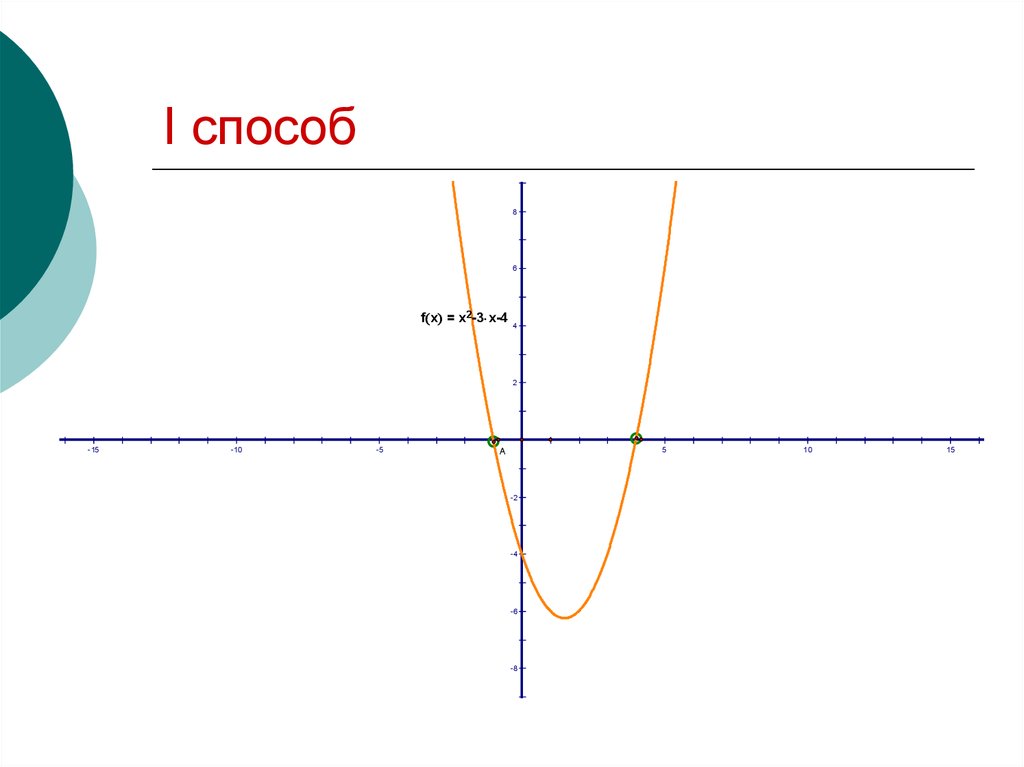
14. Геометрический способ решения квадратных уравнений

В древности геометрия была более
развита, чем алгебра.
Есть всего пять основных способов
графического решения квадратных
уравнений.

15. I способ

8
6
f x = x2-3 x-4
4
2
-15
-10
-5
5
A
-2
-4
-6
-8
10
15

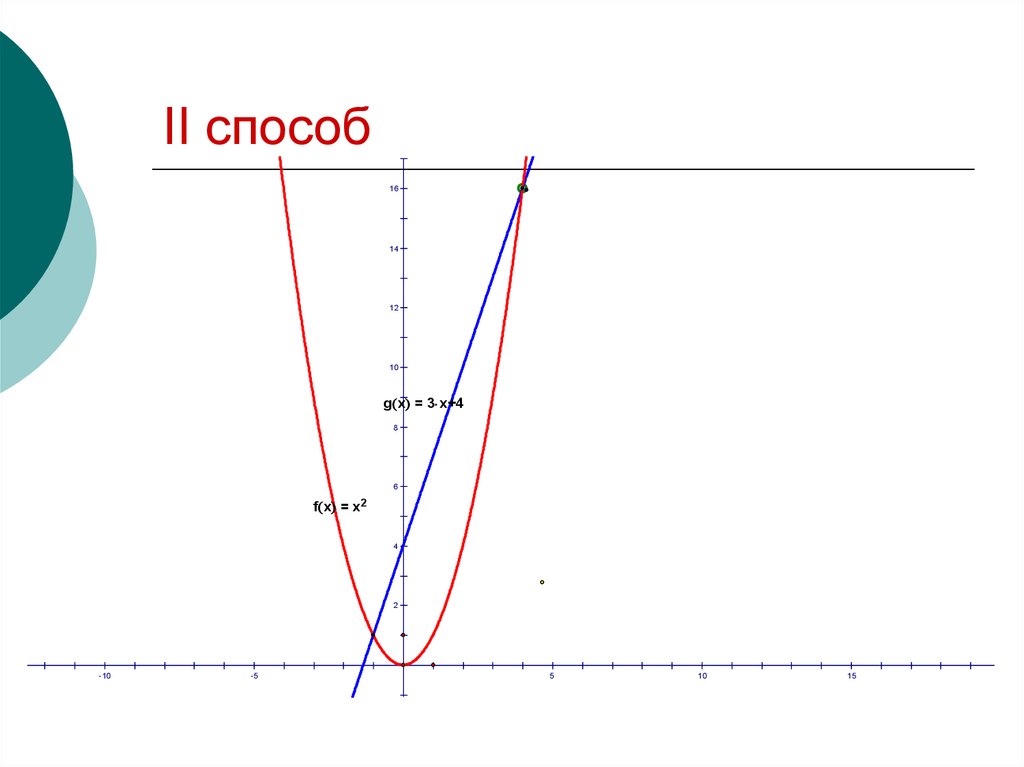
16. II способ

16
14
12
10
g x = 3 x+4
8
6
f x = x2
4
2
-10
-5
5
10
15

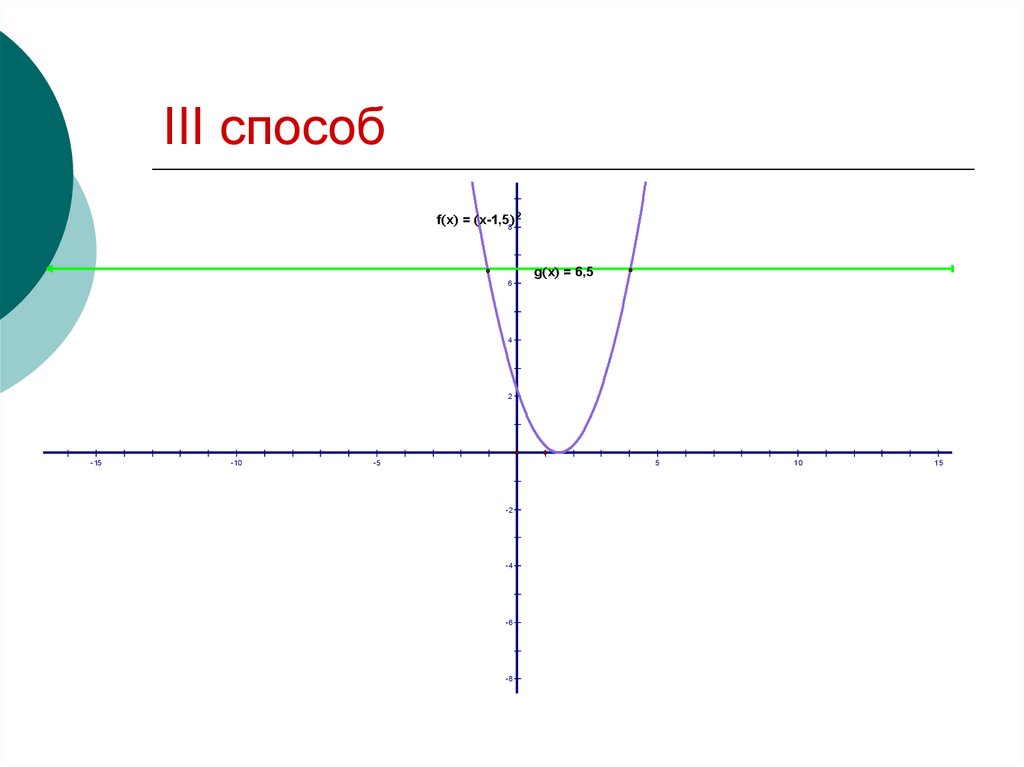
17. III способ

f x = x-1,58 2
g x = 6,5
6
4
2
-15
-10
-5
5
-2
-4
-6
-8
10
15

18. IV способ

12
10
8
6
f x = x2-4
4
g x = 3 x
2
-15
-10
-5
5
-2
-4
10
15

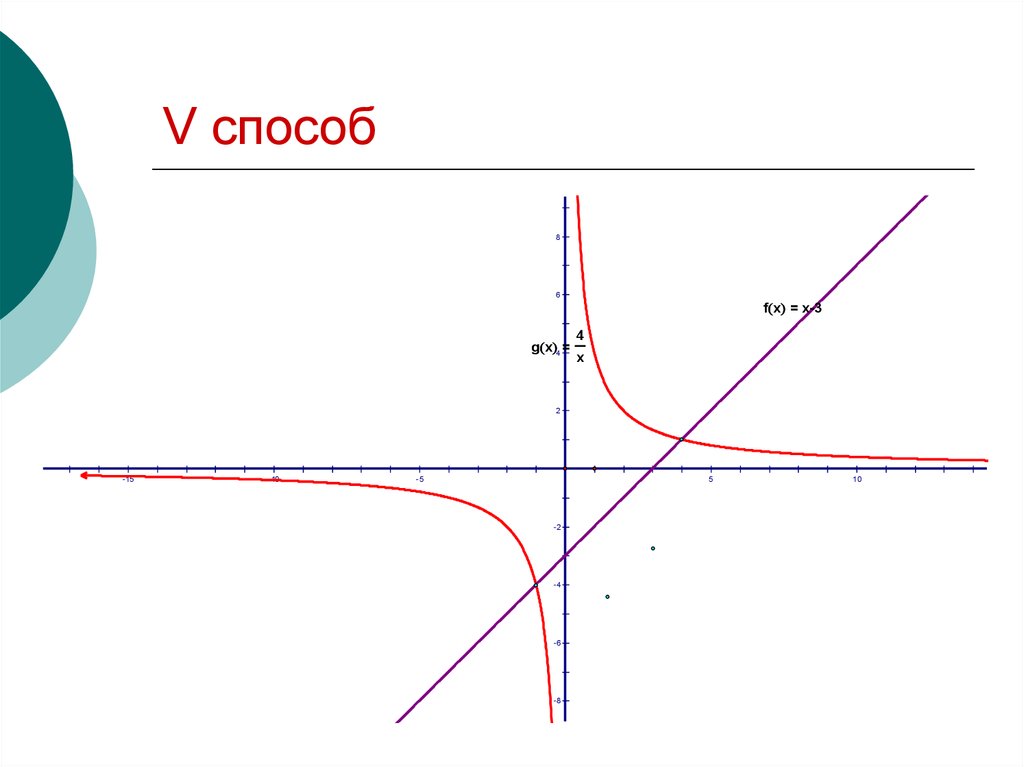
19. V способ

8
6
g x 4 =
f x = x-3
4
x
2
-15
-10
-5
5
-2
-4
-6
-8
10