Космические задачи. Подготовка к ЕГЭ и ГИА

Невозможно постичь тайны природы и
оценить ее красоту, не понимая языка, на
котором она говорит, а говорит она на языке
математики .
Данный урок показывает необходимость
применения математических знаний в
космонавтике, а также будет полезен при
подготовке к ГИА по математике. Поехали.

3.

7,9 <
v (эллипс)
< 11,2 км/сек.
v = 7,9 км/сек.
(круговая орбита)
v < 7,9 км/сек.
(траектория тела,
падающего на Землю)

4.

Высота над землей подброшенного вверх мяча
меняется по закону h(t ) 1,6 8t 5t 2 , где h –
высота в метрах, t – время в секундах,
прошедшее с момента броска. Сколько секунд
мяч будет находиться на высоте не менее трех
метров?
Решим неравенство :
1,6 8t 5t 2 3
5t 8t 1,4 0
2
+
-
0,2
+
1,4
t
1,4-0,2=1,2
Ответ: 1,2

5.

Система навигации, встроенная в спинку
самолетного кресла, информирует пассажира о
том, что полет проходит на высоте 37 170
футов. Выразите высоту полета в метрах.
Считайте, что 1 фут равен 30,5 см.
Решение:
1) 37 000 • 30,5 = 1 128 500 см
(37 • 30 + 18,5) •1000= 1128,5 •1000
2) 1 128 500 : 100 = 11 285 м
Ответ: 11285

6.

Расстояние (в км) от наблюдателя, находящегося на
небольшой высоте h м над землeй, выраженное в
километрах, до наблюдаемой им
Rh
l
линии горизонта вычисляется по формуле
500
,
где R=6400 км — радиус Земли. На какой наименьшей
высоте следует располагаться наблюдателю, чтобы он видел
горизонт на расстоянии не менее 4 километров? Ответ
выразите в метрах.
Решим уравнение:
h
6400h
4 ,
500
R
h=1,25 м
Ответ: 1,25

7.

12 апреля 1961 года в 09 часов 07 минут с
космодрома Байконур стартовала ракетаноситель «Восток». Полёт продолжался 108
минут. Когда приземлился «Восток» на землю?
(недалеко от деревни Смеловка, которая
расположена в Саратовской области).Ответ
дайте в минутах.
Ответ: 655

8.

12 апреля 1961года Ю. А. Гагарин на
космическом корабле «Восток» был поднят над
землей на максимальную высоту 327 км. На
каком расстоянии от корабля находились в это
время наиболее удаленные от него и видимые
космонавтом участки поверхности Земли?
В
Решение:
Из ▲ ОКВ- прям:
?
ВК ОВ ОК
2
2
ВК 6727 6400
2
2
327 13127 2072км
2
327
А
К
6400 км
О

9.

При движении ракеты еe видимая для
неподвижного наблюдателя длина, измеряемая в
метрах, сокращается по
2
v
закону l l0 1- c 2, где l0 = 5 м — длина
5
покоящейся ракеты, c = 3·10 км/с — скорость
света, а v — скорость ракеты (в км/с). Какова
должна быть минимальная скорость ракеты,
чтобы еe наблюдаемая длина стала не более 4 м?
Ответ выразите в км/с.

10.

Найдем, при какой скорости длина ракеты
станет равна 4 м.
Решим уравнение.
2
2
v
l0 1 2 4
c
81 10
v 10
25
2
,
,
v
5 1
4
10
9 10
v 180000км / c
Ответ: 180000

11.

Вычислите
длину круговой
орбиты
искусственного
спутника Земли,
если спутник
вращается на
расстоянии
320 км от Земли,
а радиус Земли
равен 6370 км.
?
C = 2 π r, C = π d
C≈2•3,14•6690≈42013км

12.

1) Длина экватора Луны приближенно равна
10,9 тыс. км.
Чему равна площадь поверхности Луны?
2
C =10,9=3,14d ;D≈3,47; R ≈1,74 тыс.км
R
S=4
π
С= 2πR

13.

d≈3,47 тыс. км , r≈1,74 тыс.км,
S≈38млн.кв.км
2) Площадь поверхности Луны приближенно
составляет 7,45% площади поверхности Земли.
Найдите площадь поверхности Земли. (Результат
округлите до млн. кв. км)
S≈506млн.кв.км

14.

Диаметр Луны составляет приблизительно ¼
диаметра Земли. Сравните объемы Луны и
Земли, считая их шарами.
4 3
V R
3
V3
3
4 64
Vл

15.

Для определения эффективной температуры звёзд используют
закон Стефана–Больцмана, согласно которому мощность
излучения нагретого тела P, измеряемая в ваттах,
прямо пропорциональна площади его поверхности и четвертой
степени температуры:
8
P = σSТ , где σ = 5,7 ∙ 10 — постоянная, площадь S
измеряется в квадратных метрах, а температура T — в градусах
Кельвина. Известно, что некоторая звезда имеет площадь
4
1
20
S 10 м2, а излучаемая ею
16
мощность P не менее 9,12 · 1025 Вт.
Определите наименьшую возможную температуру этой звезды.
Приведите ответ в градусах Кельвина.

16.

Подставим данные и решим уравнение: P = 9,12 · 1025
1
20
4
10 T = 9,12 · 1025
5,7 ∙ 10
16
8
9,12 10 16
8
20
5,7 10 10
25
Т
4
Т
T
=
=
256 10
=
4000 К
4
12
Ответ: 4000

17.

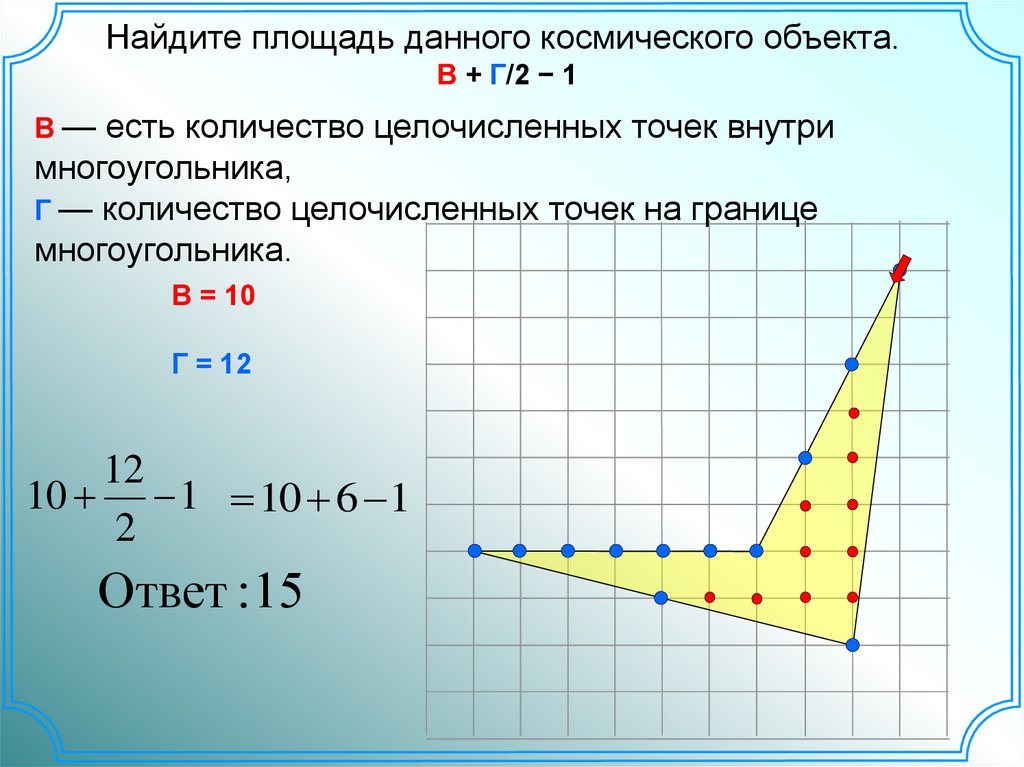
Найдите площадь данного космического объекта.
В + Г/2 − 1
В — есть количество целочисленных точек внутри
многоугольника,
Г — количество целочисленных точек на границе
многоугольника.
В = 10
Г = 12
12
10 1 10 6 1
2
Ответ :15

18.

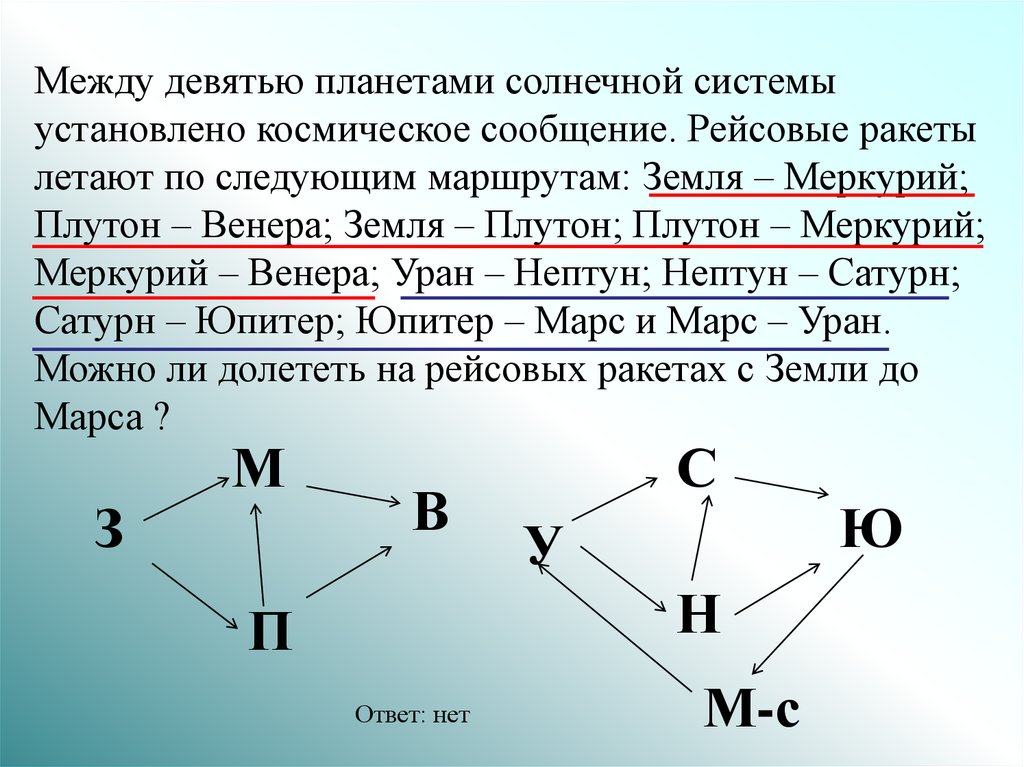
Между девятью планетами солнечной системы
установлено космическое сообщение. Рейсовые ракеты
летают по следующим маршрутам: Земля – Меркурий;
Плутон – Венера; Земля – Плутон; Плутон – Меркурий;
Меркурий – Венера; Уран – Нептун; Нептун – Сатурн;
Сатурн – Юпитер; Юпитер – Марс и Марс – Уран.
Можно ли долететь на рейсовых ракетах с Земли до
Марса ?
З
М
В
С
У
Н
П
Ответ: нет
М-с
Ю

English Русский Правила