Похожие презентации:
Из истории числа
1. Из истории числа
Презентация для урока математикив старших классах.
Выполнила учитель математики
ГБОУ школа 94 Выборгского района
Михайлова М. А.
2.
“Нужно стремиться узнатьпуть, часто непрямой и
трудный, которым шли
первые изобретатели,
чтобы понять, сколь
многим мы обязаны этим
истинным благодетелям
человека”.
Жан Луи Лагранж (1736 - 1813).
3. Число π возникло как результат несложных наблюдений. Соотношение между длиной окружности L и ее диаметром d постоянно:
длина окружностиконстанта
диаметр окружности
L
const
d
L d
e i e ei ( греч.) окружность (" Пи" )
4. Древний Египет
Египетский папирус Ахмеса(1650 г.
до н. э.): “Круглое поле имеет в
диаметре 9 хет (~450 метров).
Какова площадь поля?”
Решение
9 2
2 64
( ) d ;
2
81
81
2 64
d ;
4
81
256
3,16...
81
S кв адрата(a 8) S круга (d 9)
Площадь квадрата со стороной 8 равна S круга с диаметром 9
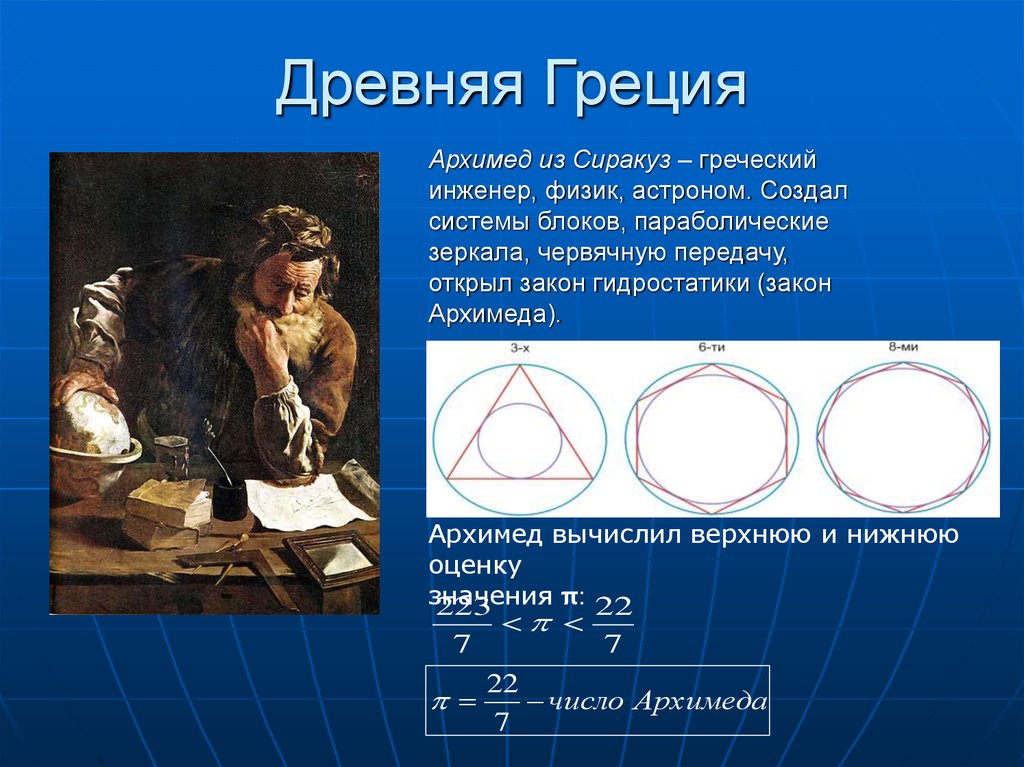
5. Древняя Греция
Архимед из Сиракуз – греческийинженер, физик, астроном. Создал
системы блоков, параболические
зеркала, червячную передачу,
открыл закон гидростатики (закон
Архимеда).
Архимед вычислил верхнюю и нижнюю
оценку
значения
π: 22
223
7
7
22
число Архимеда
7
6. Китай
736Чань Цан (220 г. до н.э.)
3,1724...
232
Чжан Хэн (78-189 гг. до н.э.)
Шар вписан в куб.
Лю Хуэй (220-280 гг.)
Цзу Чунчжи (429-500 гг.)
π = 3,141592104…
3,1415926<π<3,1415927
7. Индия
1)”Шатапатха брахманы”(9 век до н.э.)
339
3,13888...
108
2)Брахмагупта (598-665 гг.)
10 3,162277...
3917
3)Бхаскара II (1114-1185 гг.)
3.1416...
1250
4)Мадхава (1350-1425 гг.)
1 1 1 1
1 ...
4
3 5 7 9
Вычислил π до 13-го знака.
8. Средняя Азия
аль-Хорезми (787-850 гг.) –математик и астроном.
“Книги о восполнении и
противопоставлении”
Использовал в простых
расчетах π=3,14, а в сложных
–
3,1416.
Джамшид ал-Каши (1380-1429) персидский ученый.
2 6
16 59 28 1 34 51
2 3 4 5 6 ...
60 60 60 60 60 60
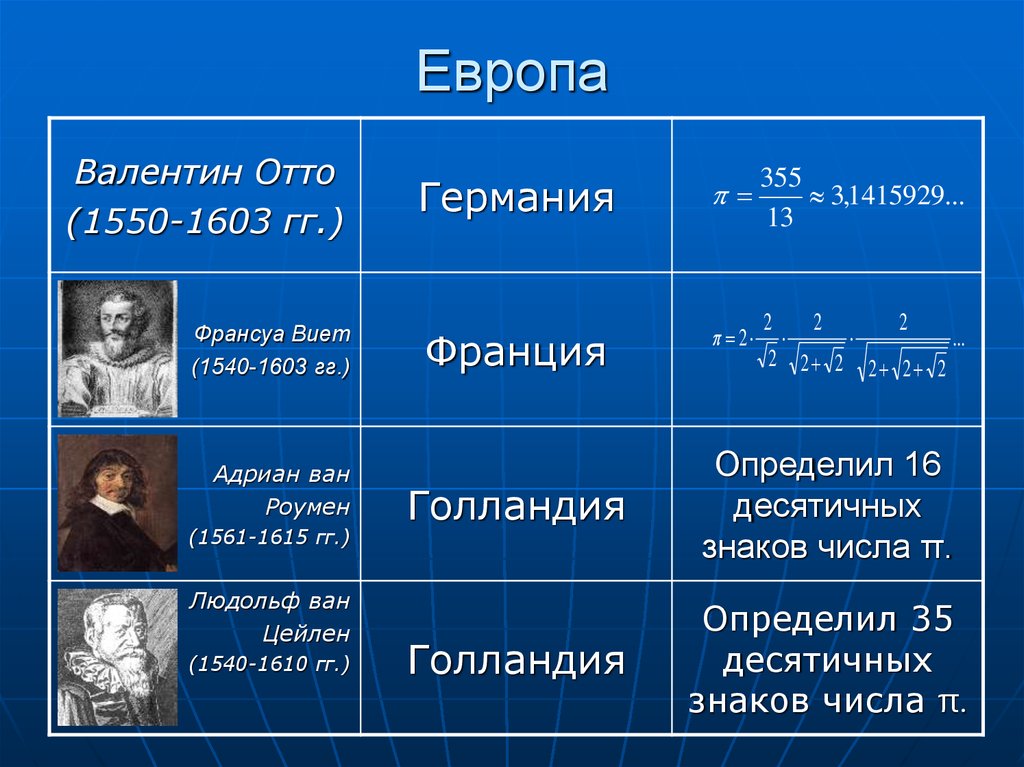
9. Европа
Валентин Отто(1550-1603 гг.)
Франсуа Виет
(1540-1603 гг.)
Адриан ван
Роумен
(1561-1615 гг.)
Людольф ван
Цейлен
(1540-1610 гг.)
Германия
355
3,1415929...
13
Франция
2
2
2
2
...
2 2 2 2 2 2
Голландия
Определил 16
десятичных
знаков числа π.
Голландия
Определил 35
десятичных
знаков числа π.
10.
Адриан Антониш(1543-1620 гг.)
Христоф
Гринбергер
(1561-1636 гг.)
Венгрия
377
333
120
106
Австрия
Рассчитал 39
десятичных
знаков.
Адриан Метиус
(1571-1635 гг.)
Голландия
Исаак Ньютон
(1643-1727 гг.)
Англия
Джон Мэчин
(1686-1751 гг.)
355
3,14159292...
113
3 3
1
1
1
1
24 ( 5
...
7
12 5 2 28 2 72 29
Англия
1
1
4arctg arctg
4
5
239
Рассчитал π до 100-го
знака.
11.
Георг Вега(1754-1802 гг.)
Иоганн Генрих
Ламберт
(1728-1777 гг.)
Иоганн Захария
Дазе
(1824-1861 гг.)
Леонард Эйлер
(1707-1783 гг.)
Уильям Резерфорд
(1798-1871 гг.)
4
Словения
Германия
5arctg
1
3
2arctg
7
79
Рассчитал π до 137
знаков.
Доказал, что число
π- иррационально.
Германия
1
1
1
arctg arctg
4
2
5
8
Рассчитал 200 десятичных
знаков.
Россия
Предположил, что
число πтрансцендентно.
Шотландия
Получил 440
десятичных знаков
arctg
12. Что такое трансцендентное число?
Число называется алгебраическим,если
оно является
a x n a корнем
x n 1 ...многочлена
a x a ,
n
n 1
1
0
an ; an 1; ...a1; a0
все коэффициенты которого
рациональные числа.
Неалгебраическое число называется
Трансцендентным
13.
11
4arctg arctg
4
5
239
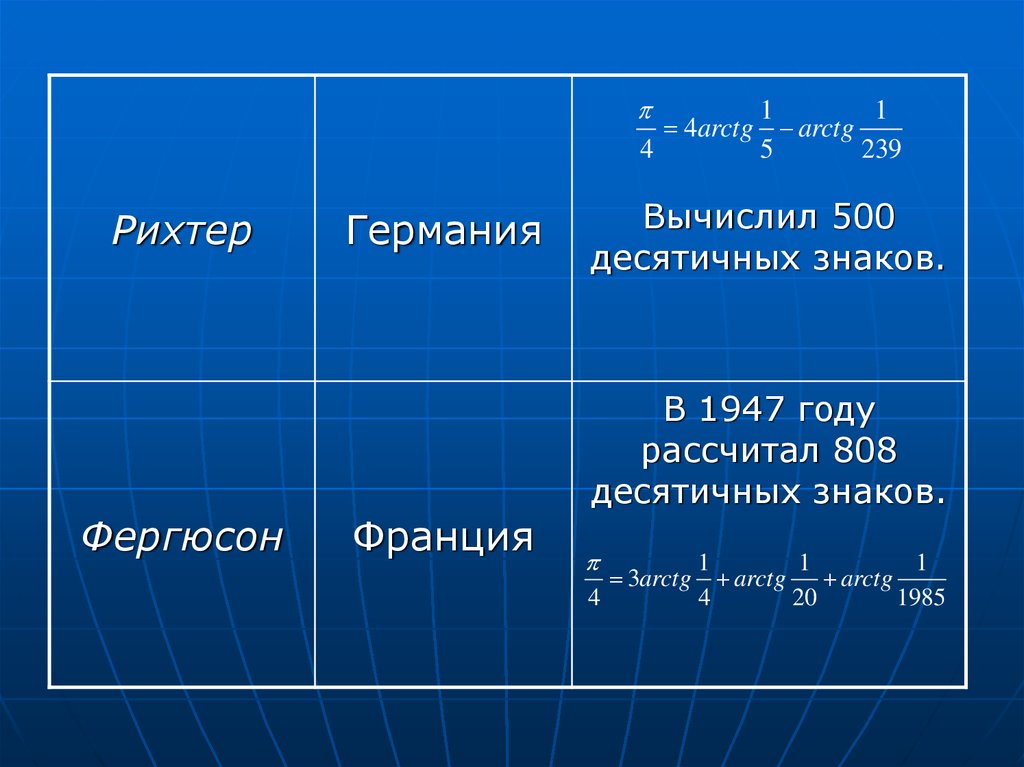
Рихтер
Германия
Вычислил 500
десятичных знаков.
В 1947 году
рассчитал 808
десятичных знаков.
Фергюсон
Франция
1
1
1
3arctg arctg arctg
4
4
20
1985
14.
1882 год – немецкий математик КарлЛуи фон Линдеман (1852-1939 гг.)
доказал трансцендентность числа .
Число покинуло мир
геометрии.
15. Компьютерная эра XX - XXI века
1946 год – ENIAC – Electronic NumericalIntegrator and Computer.
Вычисление первых 2037 знаков заняло
70
часов!
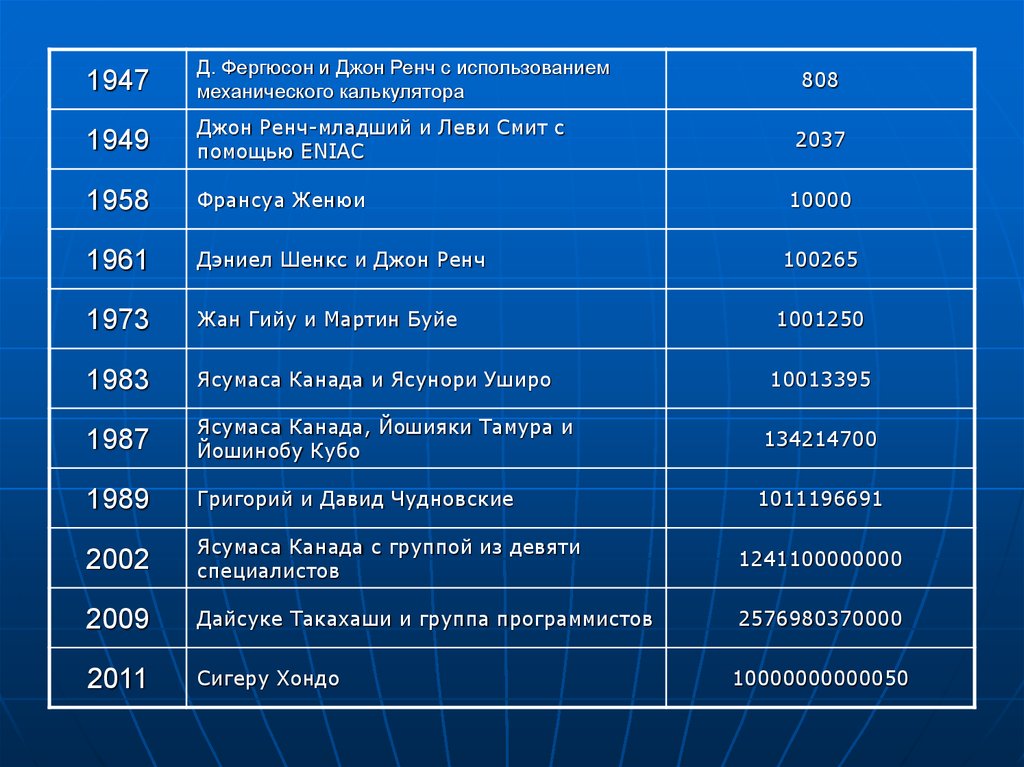
16.
1947Д. Фергюсон и Джон Ренч с использованием
механического калькулятора
1949
Джон Ренч-младший и Леви Смит с
помощью ENIAC
1958
Франсуа Женюи
1961
Дэниел Шенкс и Джон Ренч
1973
Жан Гийу и Мартин Буйе
1983
Ясумаса Канада и Ясунори Уширо
1987
Ясумаса Канада, Йошияки Тамура и
Йошинобу Кубо
1989
Григорий и Давид Чудновские
2002
Ясумаса Канада с группой из девяти
специалистов
1241100000000
2009
Дайсуке Такахаши и группа программистов
2576980370000
2011
Сигеру Хондо
808
2037
10000
100265
1001250
10013395
134214700
1011196691
10000000000050
17.
Для вычисления десятичных знаков применялисьформулы:
1973 год:
1983 год:
(n!) 2 4n
(n!) 2 4n
1
864
1824
20
arctg
n 1
n 1
329
n 0 (2n 1)! 325
n 0 ( 2n 1)! 3250
1
1
1
1
12arctg 32arctg 5arctg
12arctg
4
49
57
239
110443
1
1
1
1
44arctg 7arctg
12arctg
24arctg
4
57
239
682
120943
Формула Фабриса Беллара (род. в 1972 году):
1 ( 1) n 25
1
28
26
22
22
1
6 10n (
)
2 n 0 2
4n 1 4n 3 10n 1 10n 3 10n 5 10n 7 10n 9
18.
Уже вычислен квадриллион (10^15)десятичных знаков числа .
Π=3,1415926535 8979323846 2643383279
5028841971 6939937510 5820974944
5923078164 0628620899 8628034825
3421170679 8214808651 3282306647
0938446095 5058223172 5359408128
4811174502 8410270193 8521105559 ...
19.
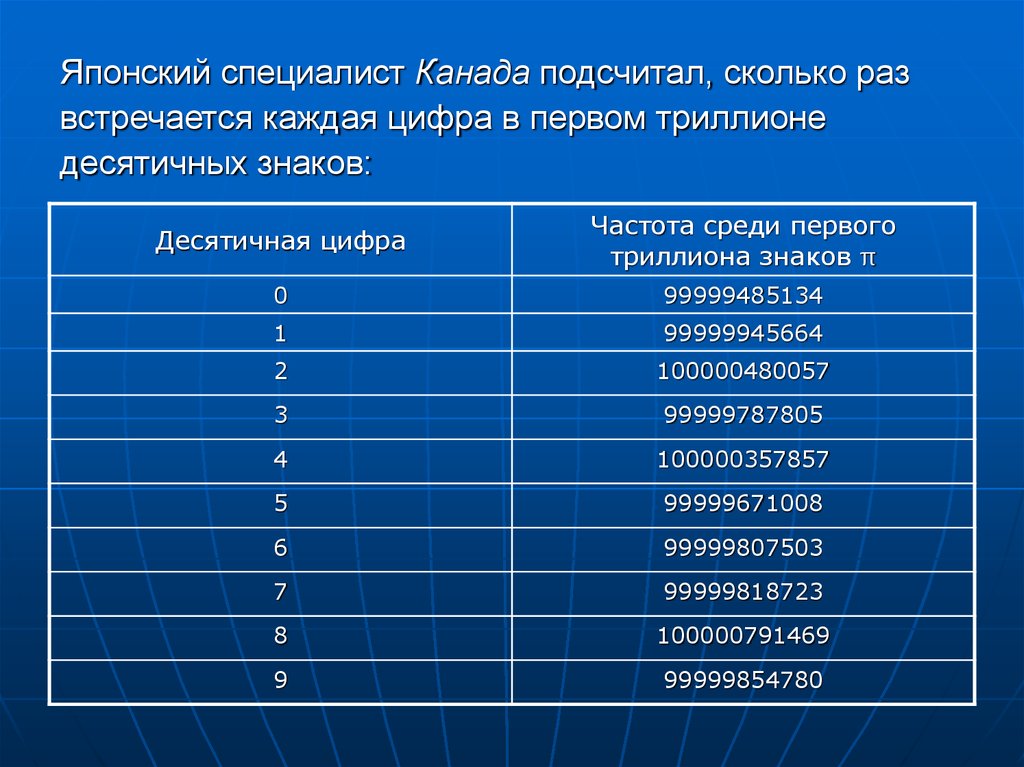
Японский специалист Канада подсчитал, сколько развстречается каждая цифра в первом триллионе
десятичных знаков:
Десятичная цифра
Частота среди первого
триллиона знаков π
0
99999485134
1
99999945664
2
100000480057
3
99999787805
4
100000357857
5
99999671008
6
99999807503
7
99999818723
8
100000791469
9
99999854780
20. Блез Паскаль (1623 - 1662 гг.)
“Предмет математикинастолько серьезен,
что полезно, не
упуская случая,
сделать его немного
занимательным”.
21. 14 Марта (3/14) – международный день числа .
14 Марта (3/14) –международный день числа .
22. Используемая литература
Школьная энциклопедияМатематика Москва, “Большая
Российская Энциклопедия”, 2006;
За страницами математики. А.
Шибасов, З. Шибасов, Москва,
“Просвещение”, 2007;
Мир математики, De Agostini,
Москва, 2014.

















 Математика
Математика








