Исследование функций с помощью производной

1. Исследование функций с помощью производной

Поречная Ирина Викторовна
учитель математики
МКОУ «Суджанская средняя
общеобразовательная школа №2»
Суджанского района
Курской области

2.

«Даже самая прекрасная и
мощная идея бесполезна до тех
пор, пока мы не решим ею
воспользоваться. Самое
интересное в идеях – это
попробовать их на деле».
Р. Бах

3.

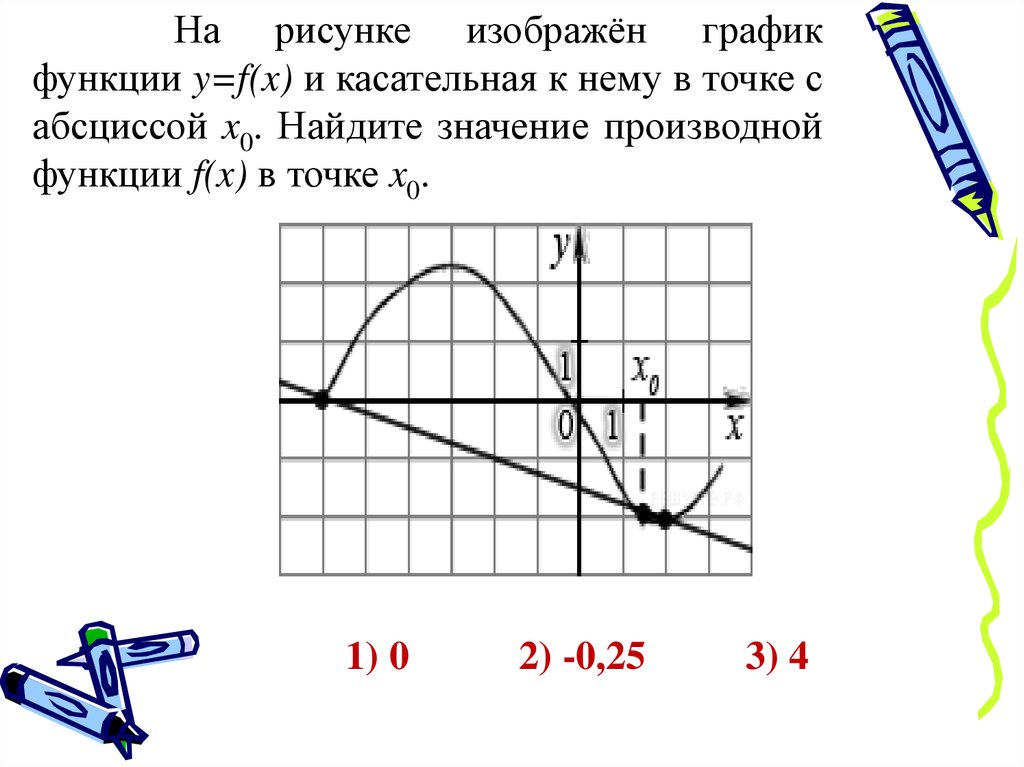
На рисунке изображён график
функции y=f(x) и касательная к нему в точке с
абсциссой x0. Найдите значение производной
функции f(x) в точке x0.
1) 0
2) -0,25
3) 4

4.

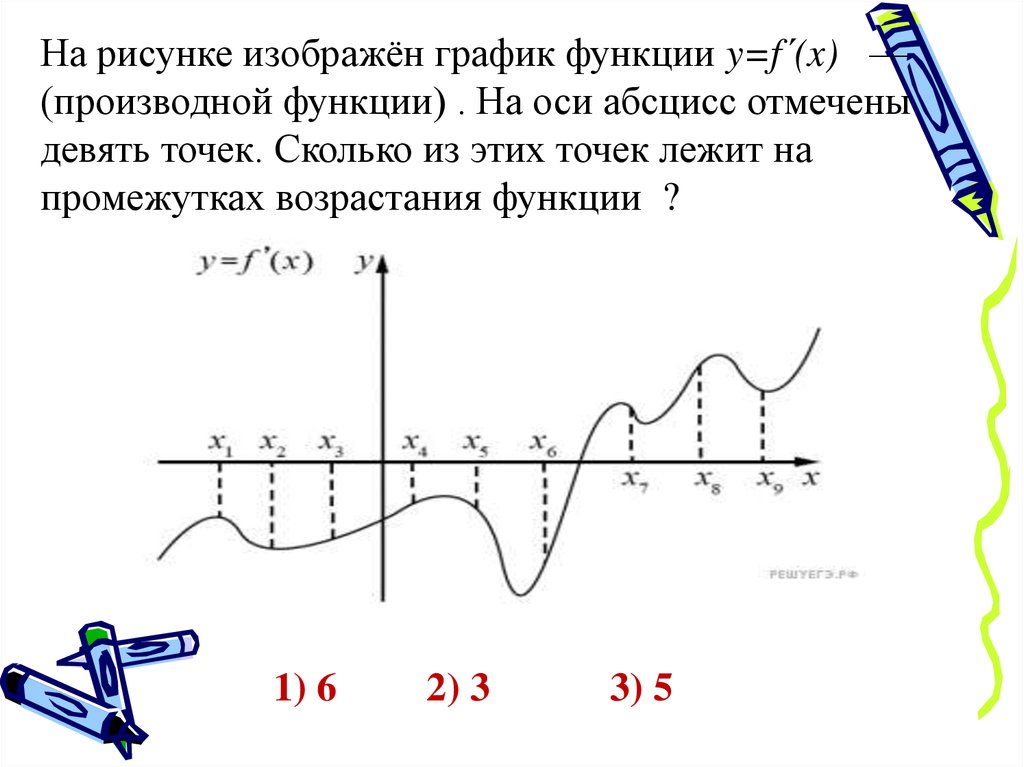
На рисунке изображён график функции y=fʹ(x) —
(производной функции . На оси абсцисс отмечены
девять точек. Сколько из этих точек лежит на
промежутках возрастания функции ?
1) 6
2) 3
3) 5

5.

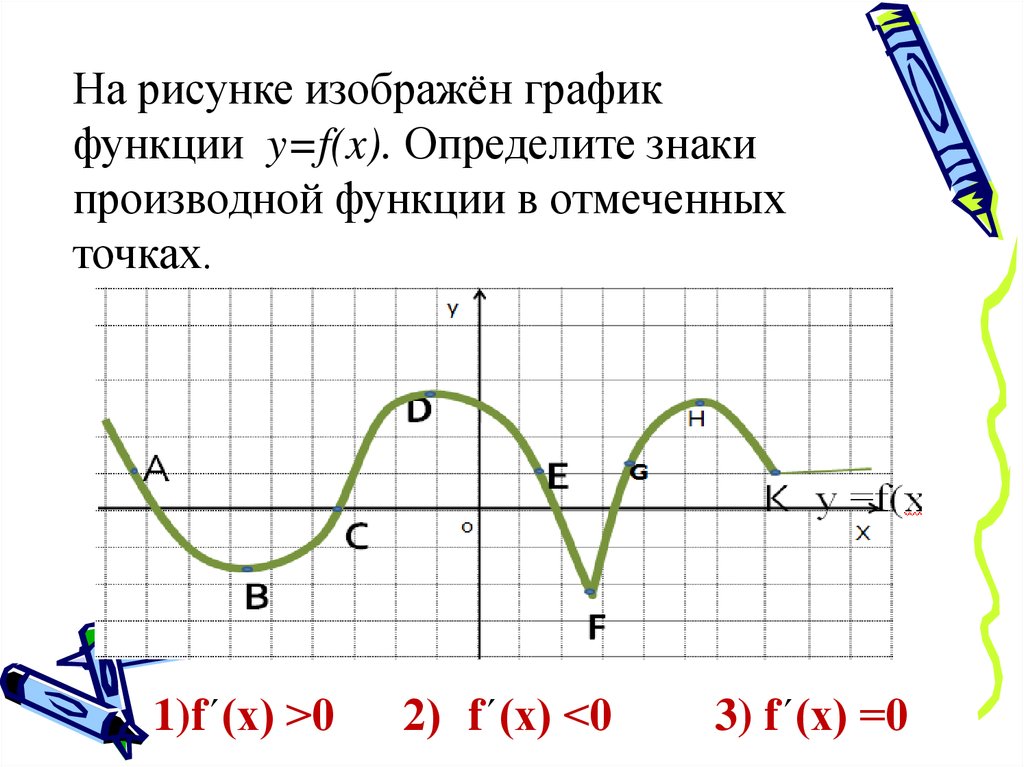
На рисунке изображён график
функции y=f(x). Определите знаки
производной функции в отмеченных
точках.
1)fʹ(х) >0
2) fʹ(х) <0
3) fʹ(х) =0

6.

На рисунке изображён график
функции y=f(x). Назовите точки
минимума этой функции?
1) х1, х3
2) х1, х4
3) х2, х4

7.

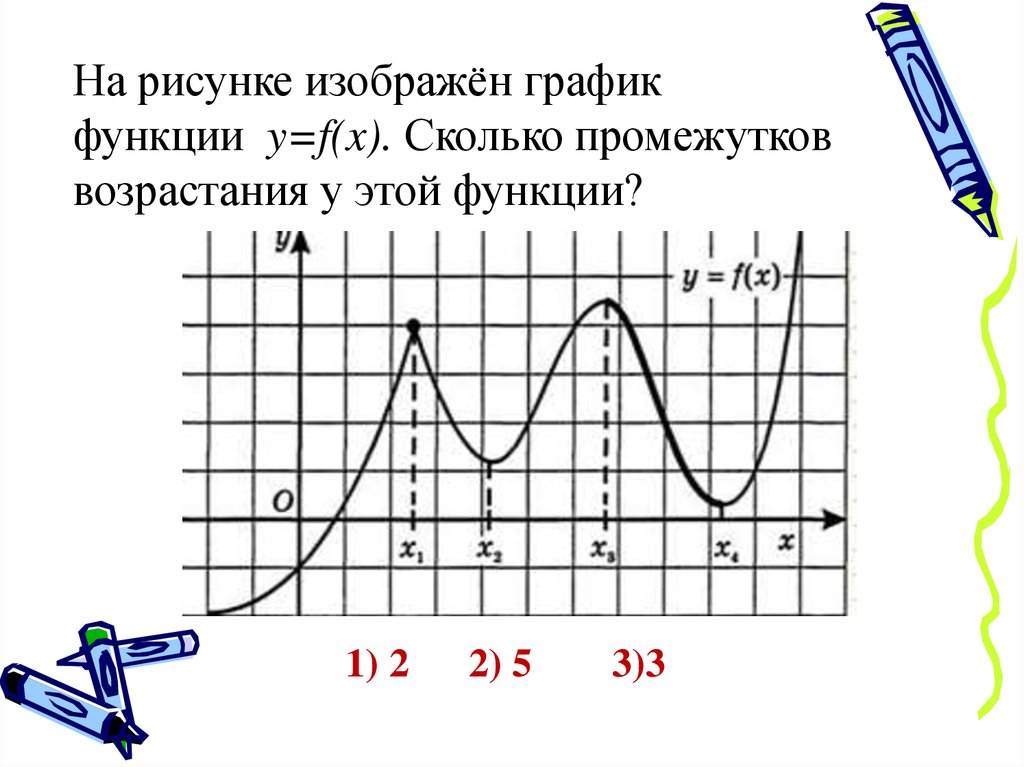
На рисунке изображён график
функции y=f(x). Сколько промежутков
возрастания у этой функции?
1) 2
2) 5
3)3

8.

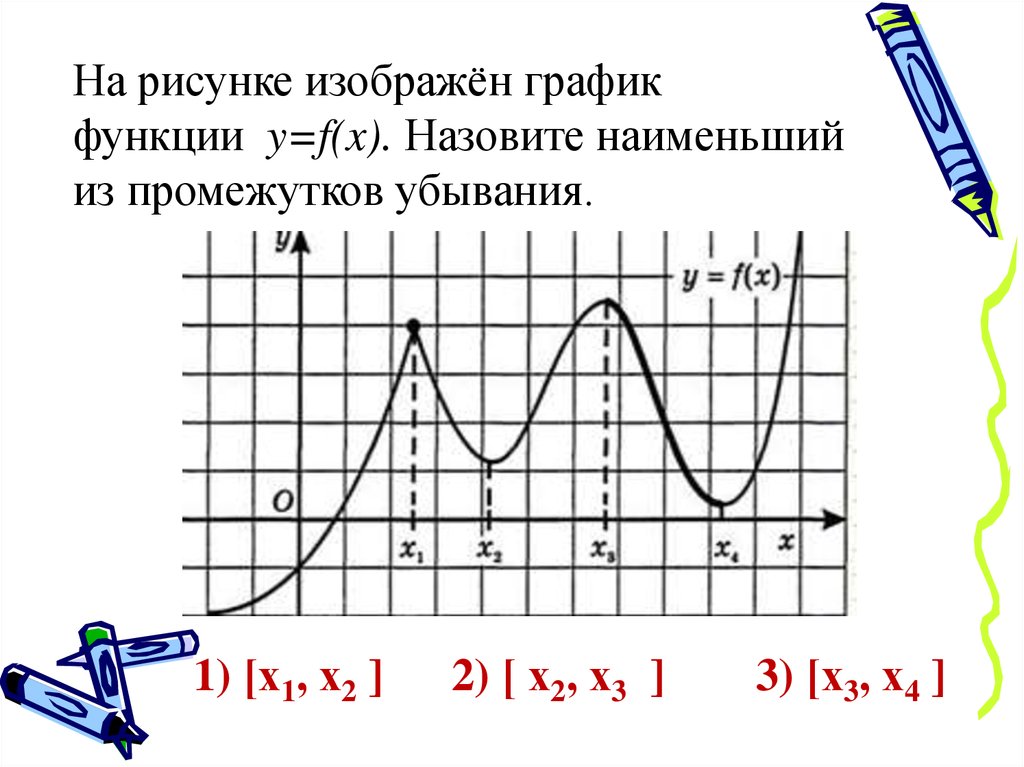
На рисунке изображён график
функции y=f(x). Назовите наименьший
из промежутков убывания.
1) [х1, х2 ]
2) [ х2, х3 ]
3) [х3, х4 ]

9.

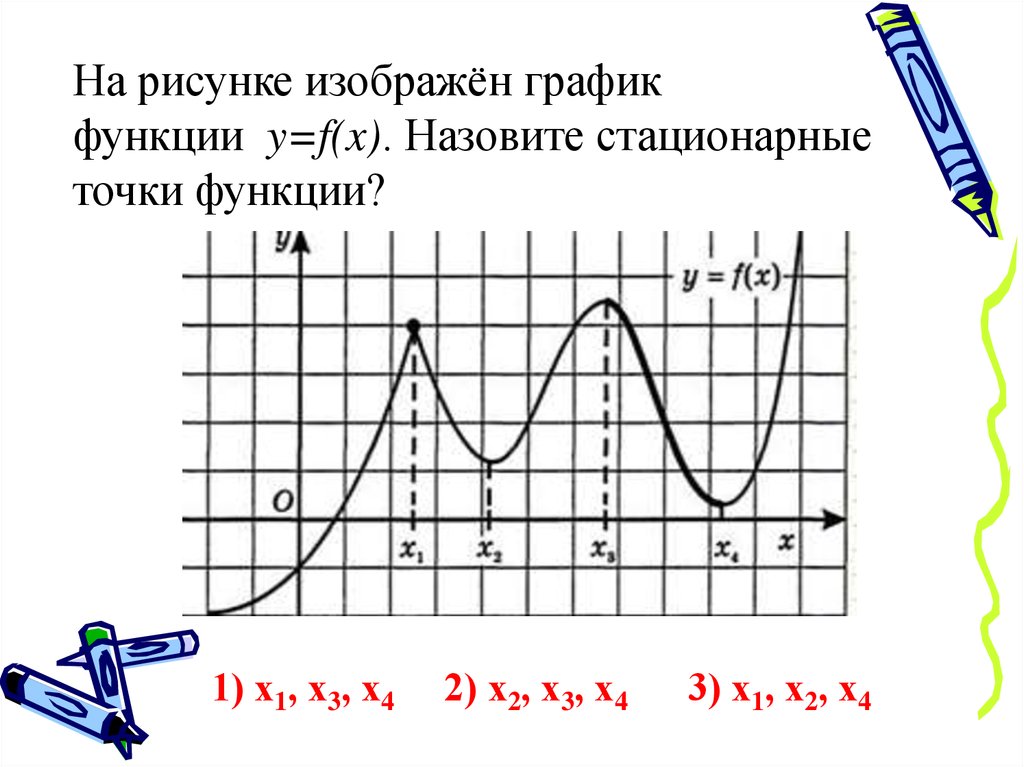
На рисунке изображён график
функции y=f(x). Назовите стационарные
точки функции?
1) х1, х3, х4
2) х2, х3, х4
3) х1, х2, х4

10.

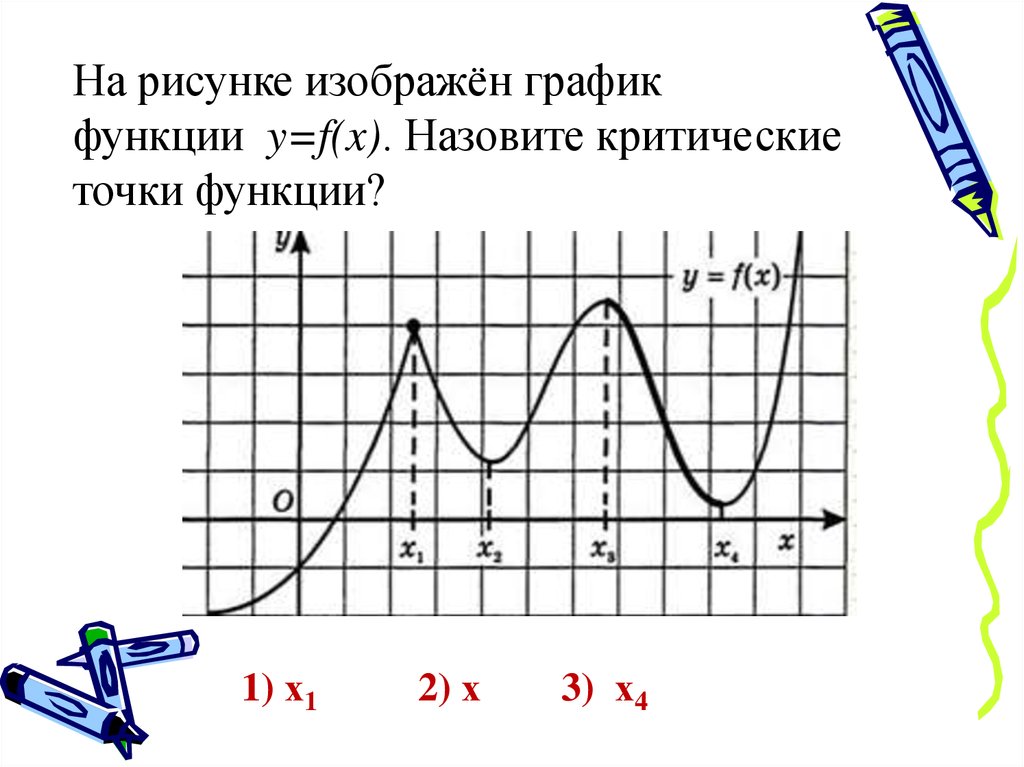
На рисунке изображён график
функции y=f(x). Назовите критические
точки функции?
1) х1
2) х
3) х4

11.

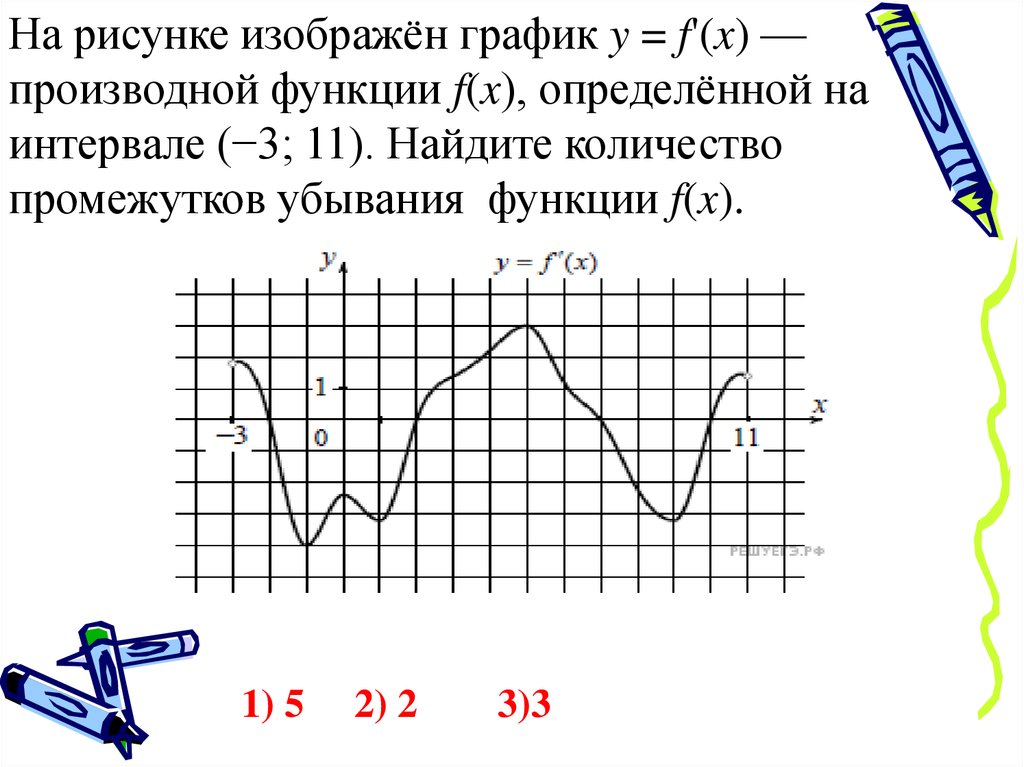
На рисунке изображён график y = f'(x) —
производной функции f(x), определённой на
интервале (−3; 11). Найдите количество
промежутков убывания функции f(x).
1) 5
2) 2
3)3

12.

Тема урока
«Исследование
функций
с помощью производной»

13.

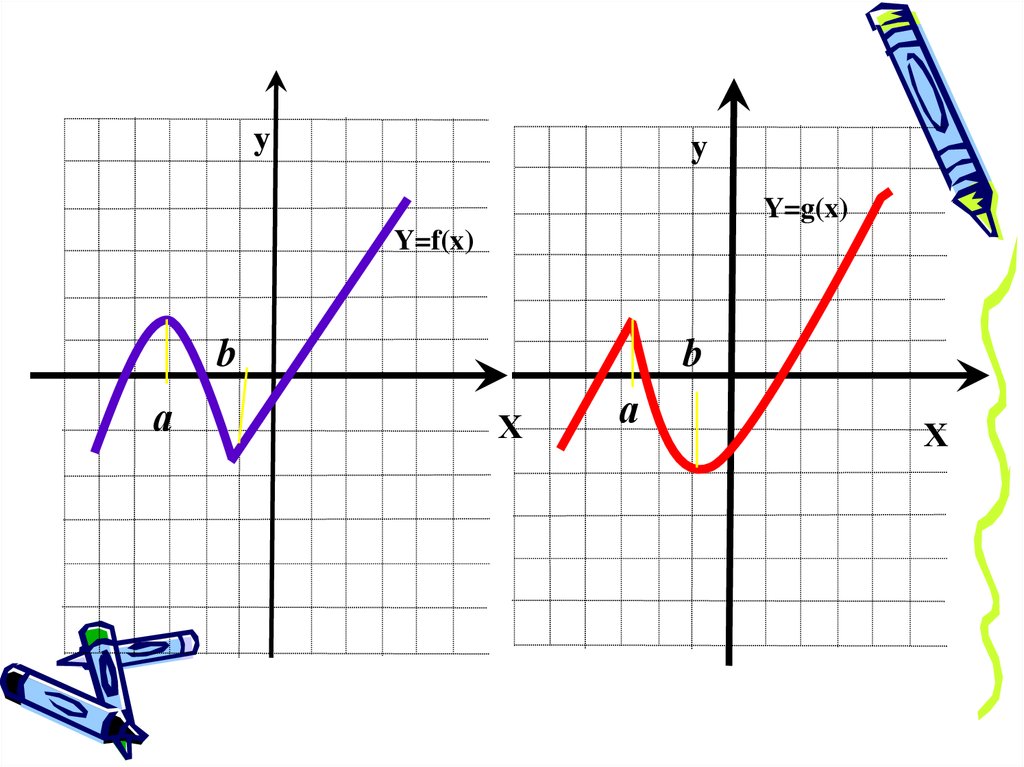
у
у
Y=g(x)
Y=f(x)
b
а
b
Х
а
Х

14.

у
у
Y=g(x)
Y=f(x)
b
а
b
Х
а
Х

15.

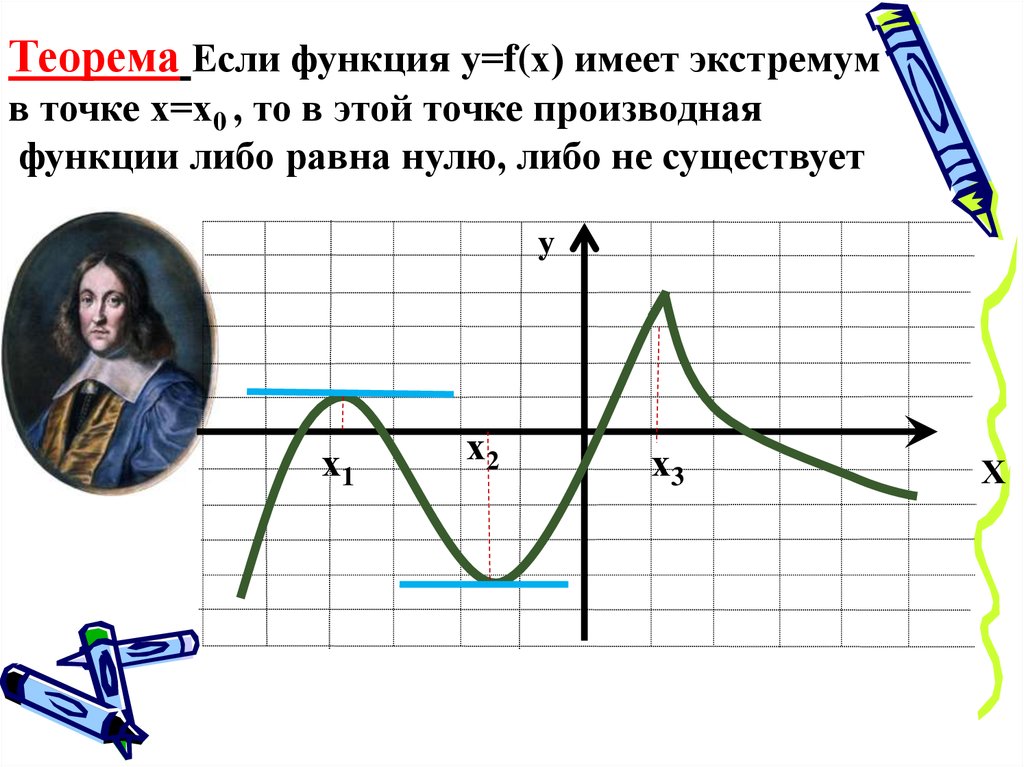
Теорема Если функция у=f(х) имеет экстремум
в точке х=х0 , то в этой точке производная
функции либо равна нулю, либо не существует
у
х1
х2
х3
Х

16.

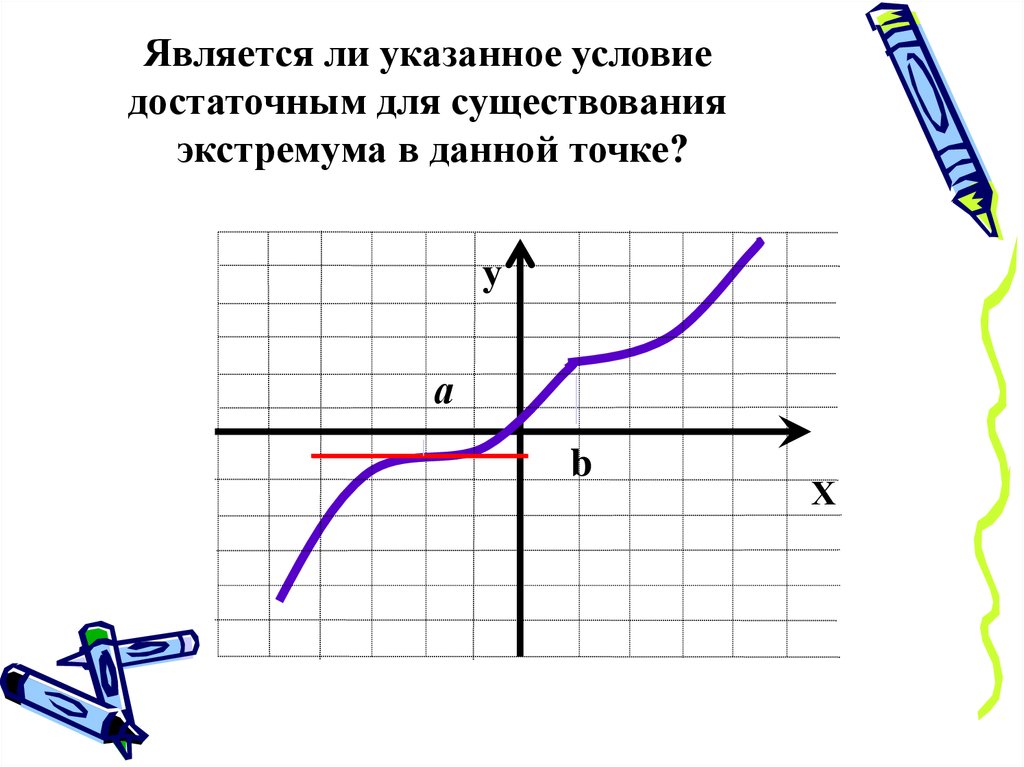
Является ли указанное условие
достаточным для существования
экстремума в данной точке?
у
а
b
Х

17.

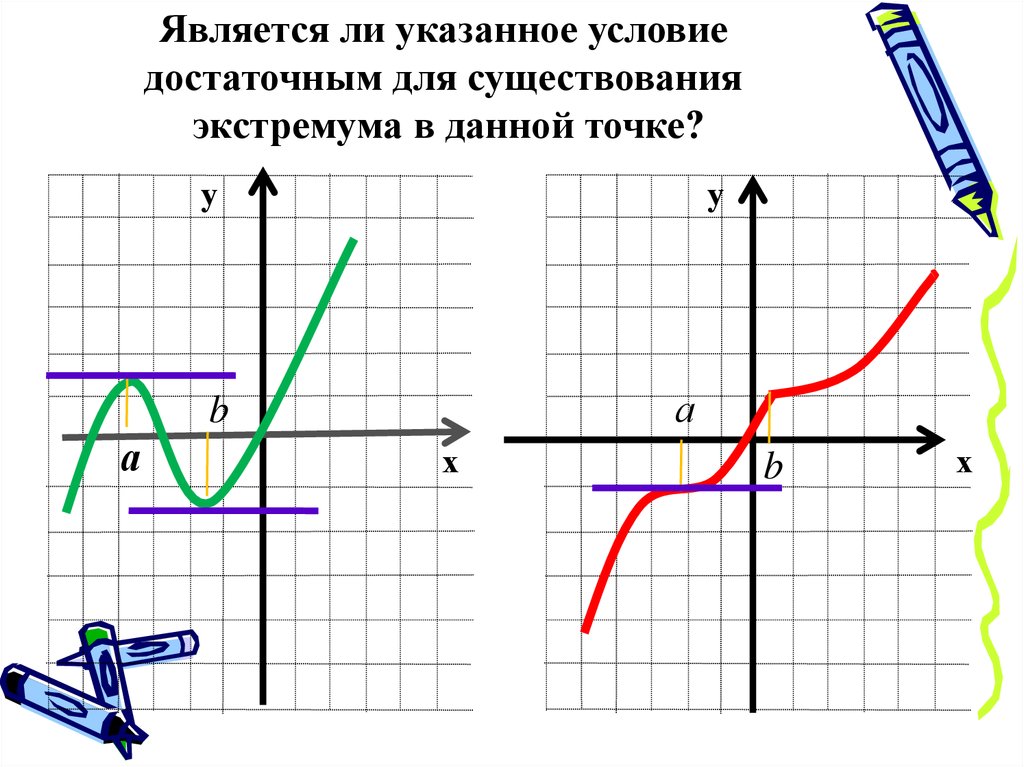
Является ли указанное условие
достаточным для существования
экстремума в данной точке?
у
у
а
b
а
х
b
х

18.

Вывод:
при переходе через точку
экстремума характер
монотонности функции
меняется

19.

Чтобы точка х была точкой
экстремума функции,
достаточно, чтобы………

20.

Теорема (достаточные условия экстремума)
Пусть функция у =f(x) непрерывна на промежутке Х и
имеет внутри промежутка стационарную или
критическую точку х =х0. Тогда:
а) если у этой точки существует такая окрестность, в
которой при x<x0 выполняется неравенство f ʹ(x)<0, а
при x>x0 - неравенство fʹ(x)>0, то х=х0 – точка
минимума функции у =f(x)
у
х0
х
fʹ(x)
f (x)
х0
точка минимума

21.

Теорема (достаточные условия экстремума)
Пусть функция у =f(x) непрерывна на промежутке Х и
имеет внутри промежутка стационарную или
критическую точку х =х0. Тогда:
б) если у этой точки существует такая окрестность, в
которой при x<x0 выполняется неравенство f ʹ(x) >0, а
при x>x0 - неравенство fʹ(x) <0, то х=х0 – точка
максимума функции у =f(x)
у
х0
х
fʹ(x)
х0
f (x)
точка максимума

22.

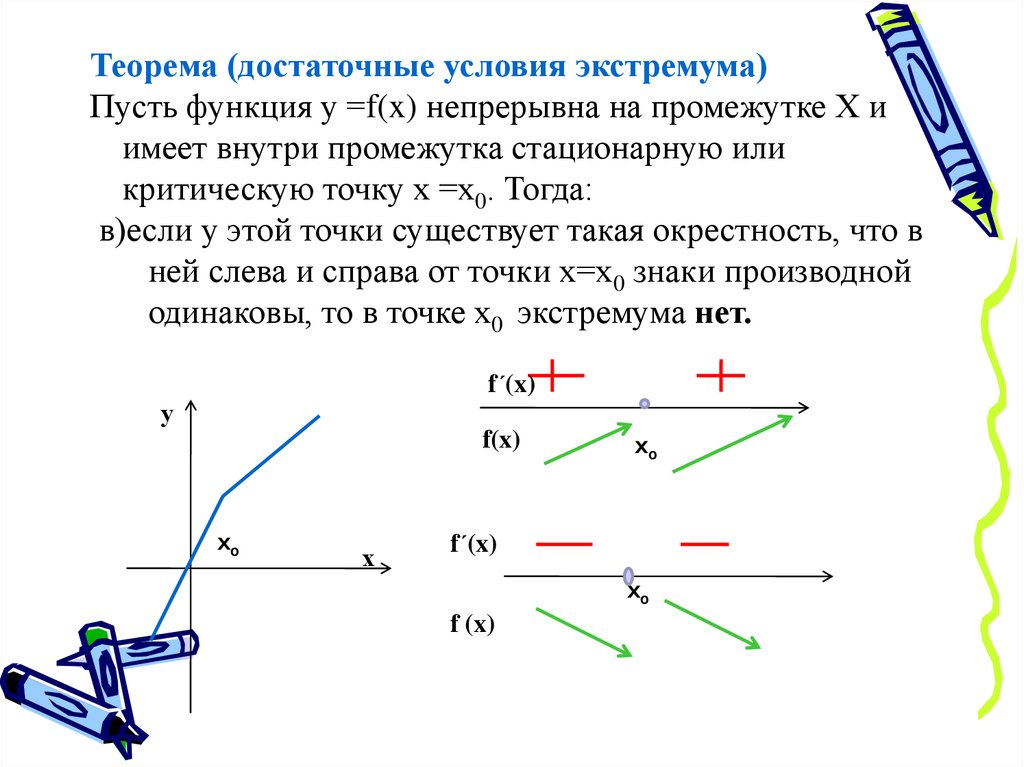
Теорема (достаточные условия экстремума)
Пусть функция у =f(x) непрерывна на промежутке Х и
имеет внутри промежутка стационарную или
критическую точку х =х0. Тогда:
в)если у этой точки существует такая окрестность, что в
ней слева и справа от точки х=х0 знаки производной
одинаковы, то в точке х0 экстремума нет.
fʹ(x)
у
f(x)
х0
х
х0
fʹ(x)
х0
f (x)

23.

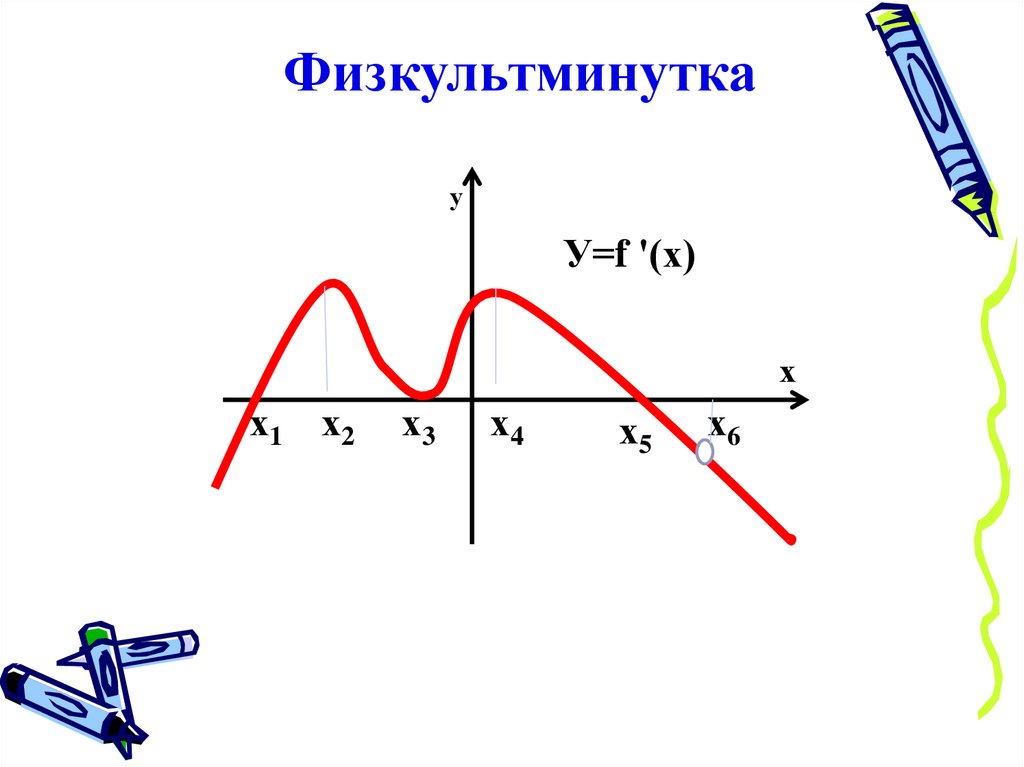
Физкультминутка
у
У=f '(х)
х
х 1 х2
х3
х4
х5
х6

24.

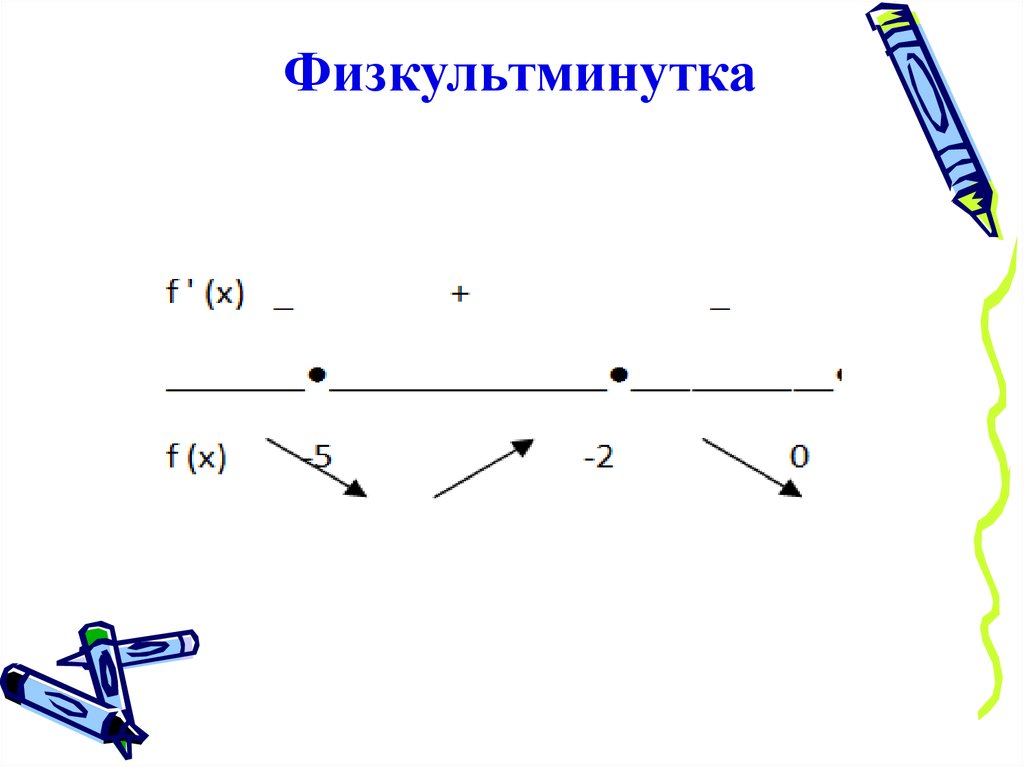
Физкультминутка

25.

На рисунке изображён график
производной.
Определяя точки
минимума, ученик указал точку х = 2.
Прав ли он?

26.

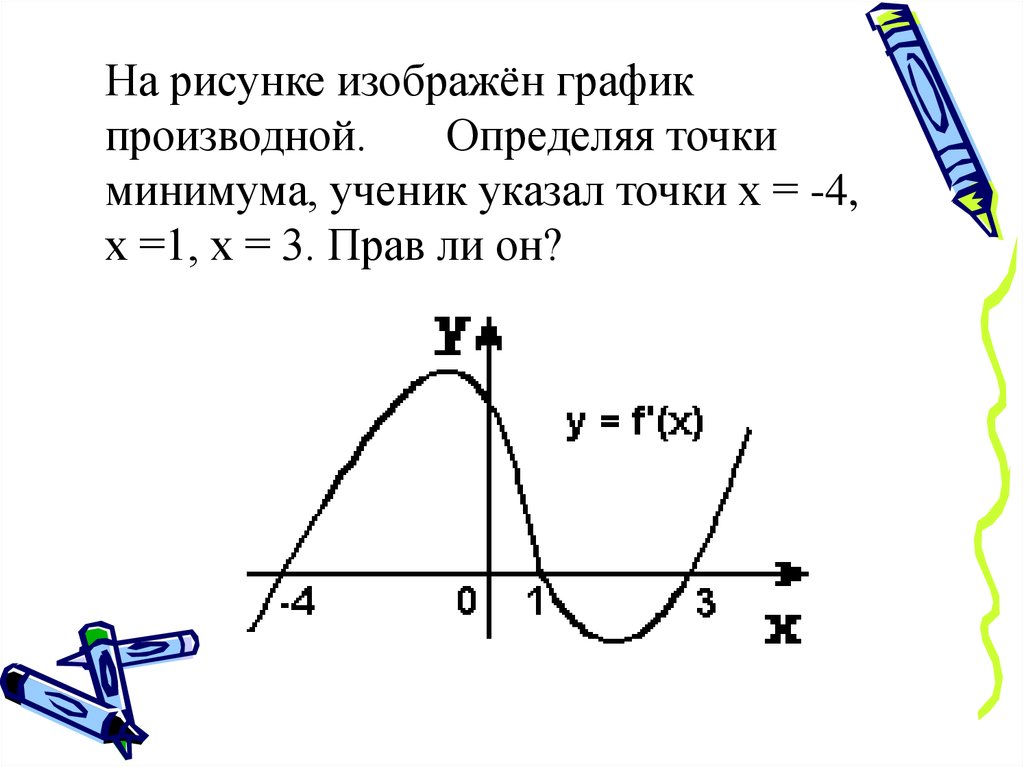
На рисунке изображён график
производной.
Определяя точки
минимума, ученик указал точки х = -4,
х =1, х = 3. Прав ли он?

27.

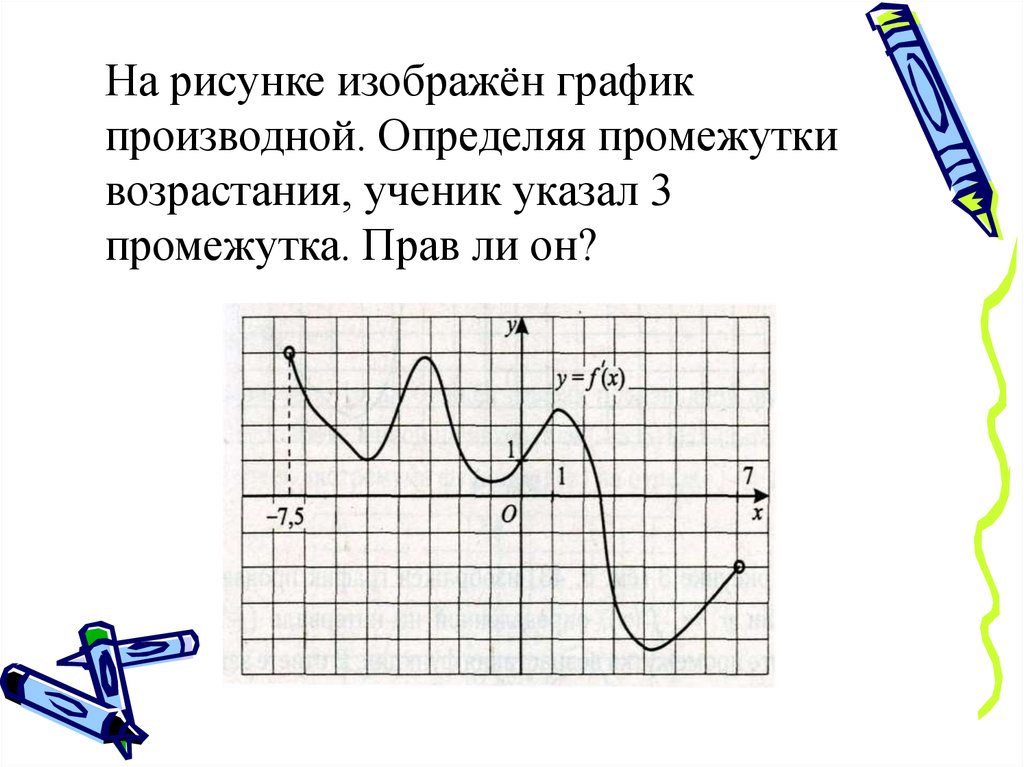
На рисунке изображён график
производной. Определяя промежутки
возрастания, ученик указал 3
промежутка. Прав ли он?

28.

На
уроке
Сегодня на уроке я узнал……..
Было интересно……….
Теперь я могу……………
Полученные знания мне пригодятся ……

29.

Домашнее задание
П.44, № 44.47, 44.48

30.

На
уроке
Зеленый –все понятно, удовлетворен
уроком, он был полезен для меня.
Желтый –есть затруднения, урок был
интересен, принимал в нем участие.
Красный –много непонятного, пользы
от урока я получил мало.