Тренажёр по теме «Производная»

1.

ТРЕНАЖЁР по теме
«ПРОИЗВОДНАЯ»
Задание № 14 базовый уровень,
№7, 12 профильный уровень

2.

3.

На рисунке изображен график производной функции у =f (x),
заданной на промежутке (- 8; 8). Исследуем свойства графика и
мы сможем ответить на множество вопросов о свойствах функции,
хотя графика самой функции не представлено!
Найдем точки, в
которых f /(x)=0 (это
нули функции).
y
+
-7 -6 -5 -4 -3 -2 -1
–
f/(x)
f(x)
-5
4
3
2
1
-1
-2
-3
-4
-5
0
y = f /(x)
+
+
–
1 2 3 4 5 6 7
3
6
x
x

4. ЗАДАНИЕ № 14

Математика
базовый уровень
ЗАДАНИЕ № 14

5.

На рисунке изображён
график функции y=f(x) и
отмечены
точки A, B, C и D на оси Ox.
Пользуясь графиком,
поставьте в соответствие
каждой точке
характеристики функции и
её производной.
1)
A
B
C
2)
3)
D
4)
значение функции в точке отрицательно, а
значение производной функции в точке
положительно
значение функции в точке положительно, а
значение производной функции в точке
отрицательно
значение функции в точке отрицательно, и
значение производной функции в точке
отрицательно
значение функции в точке положительно, и
значение производной функции в точке
положительно

6.

№ 1 На рисунке изображён график
функции y=f(x) и отмечены
точки A, B, C и D на оси Ox.
Пользуясь графиком, поставьте
в соответствие каждой точке
характеристики функции и её
производной.
A
1)
B
2)
C
3)
D
4)
значение функции в точке положительно, а
значение производной функции в точке
отрицательно
значение функции в точке отрицательно, и
значение производной функции в точке
отрицательно
значение функции в точке положительно, и
значение производной функции в точке
положительно
значение функции в точке отрицательно, а
значение производной функции в точке
положительно

7.

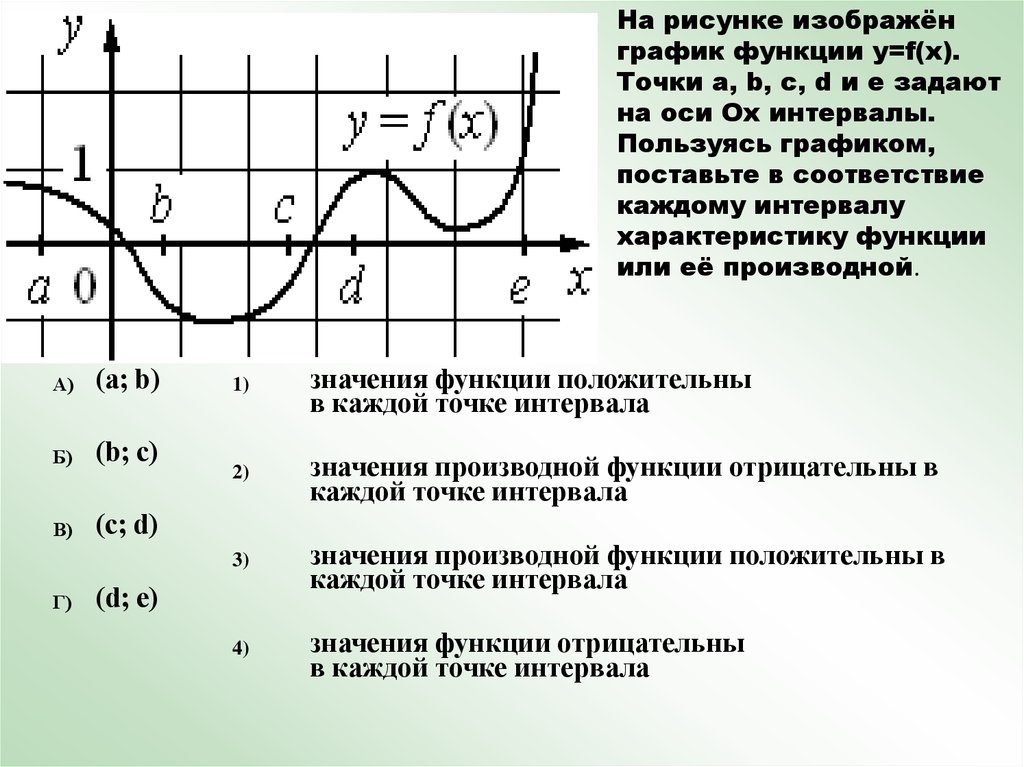
На рисунке изображён
график функции y=f(x).
Точки a, b, c, d и e задают
на оси Ox интервалы.
Пользуясь графиком,
поставьте в соответствие
каждому интервалу
характеристику функции
или её производной.
А)
(a; b)
Б)
(b; c)
В)
(c; d)
Г)
1)
значения функции положительны
в каждой точке интервала
2)
значения производной функции отрицательны в
каждой точке интервала
3)
значения производной функции положительны в
каждой точке интервала
4)
значения функции отрицательны
в каждой точке интервала
(d; e)

8.

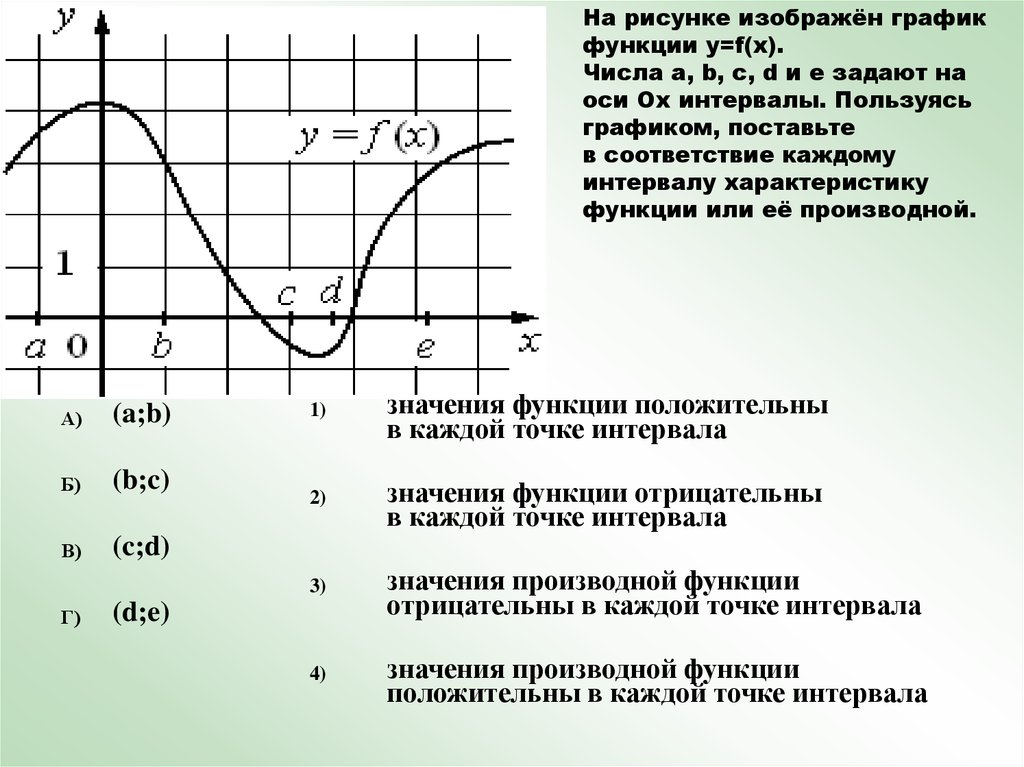
На рисунке изображён график
функции y=f(x).
Числа a, b, c, d и e задают на
оси Ox интервалы. Пользуясь
графиком, поставьте
в соответствие каждому
интервалу характеристику
функции или её производной.
А)
(a;b)
Б)
(b;c)
В)
(c;d)
Г)
1)
значения функции положительны
в каждой точке интервала
2)
значения функции отрицательны
в каждой точке интервала
3)
значения производной функции
отрицательны в каждой точке интервала
4)
значения производной функции
положительны в каждой точке интервала
(d;e)

9.

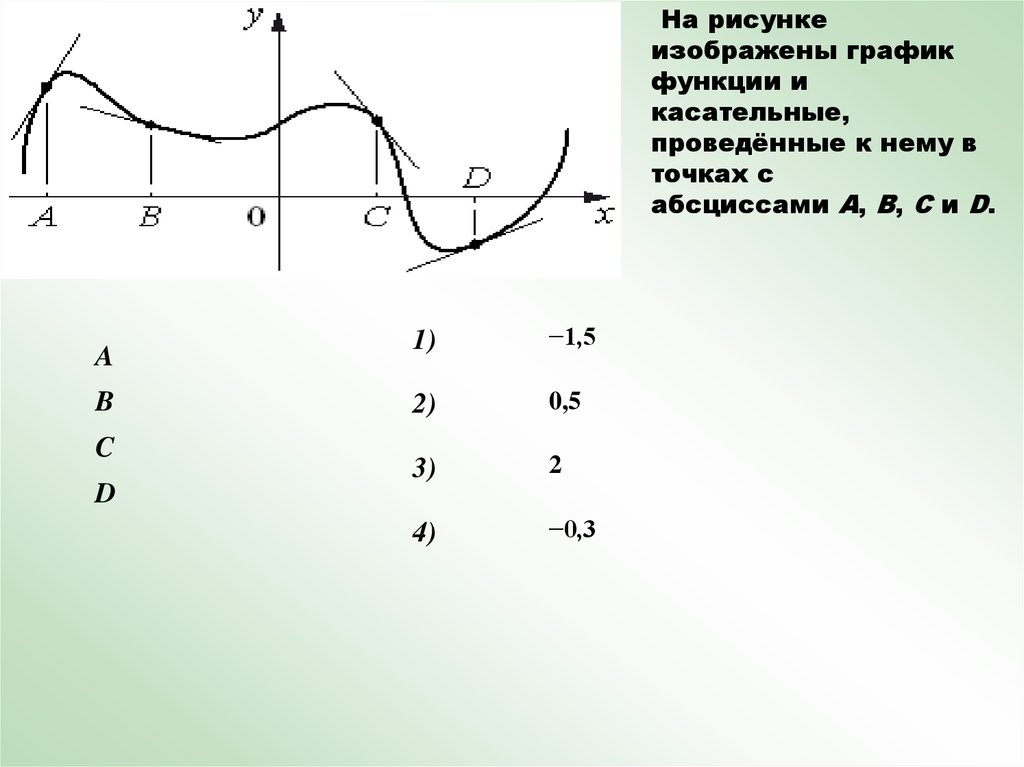
На рисунке
изображены график
функции и
касательные,
проведённые к нему в
точках с
абсциссами A, B, C и D.
A
B
C
D
1)
−1,5
2)
0,5
3)
2
4)
−0,3

10.

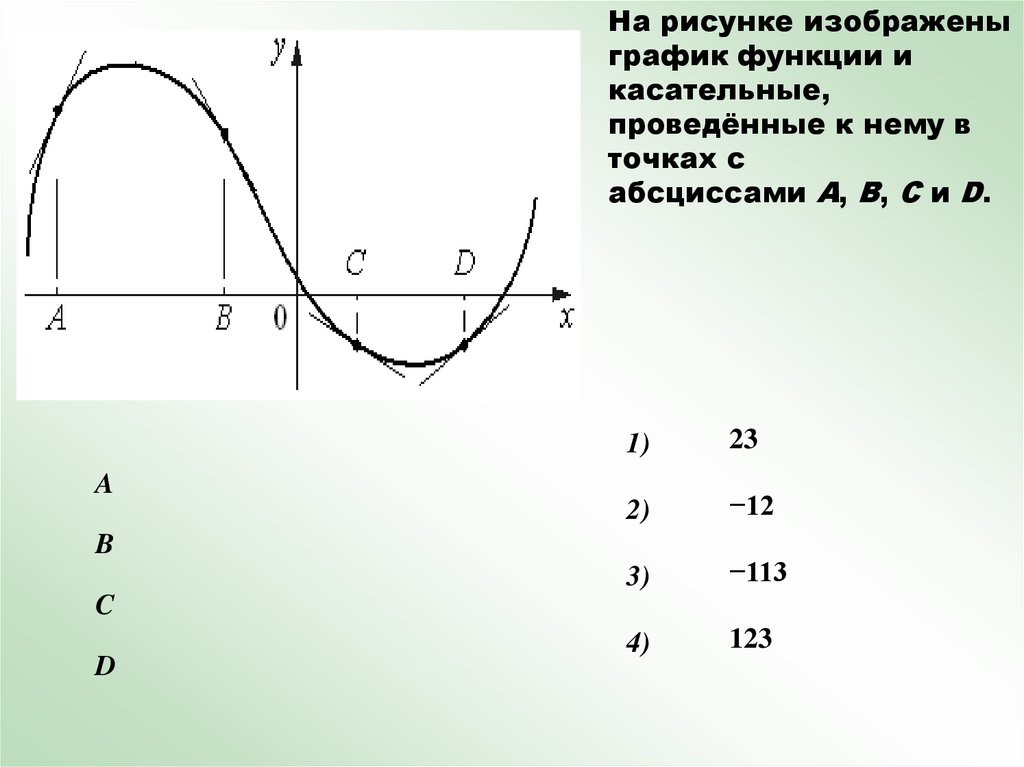
На рисунке изображены
график функции и
касательные,
проведённые к нему в
точках с
абсциссами A, B, C и D.
1)
23
2)
−12
3)
−113
4)
123
A
B
C
D

11. ЗАДАНИЕ № 7

Математика
профильный уровень
ЗАДАНИЕ № 7

12.

Задачи
на геометрический
смысл производной

13.

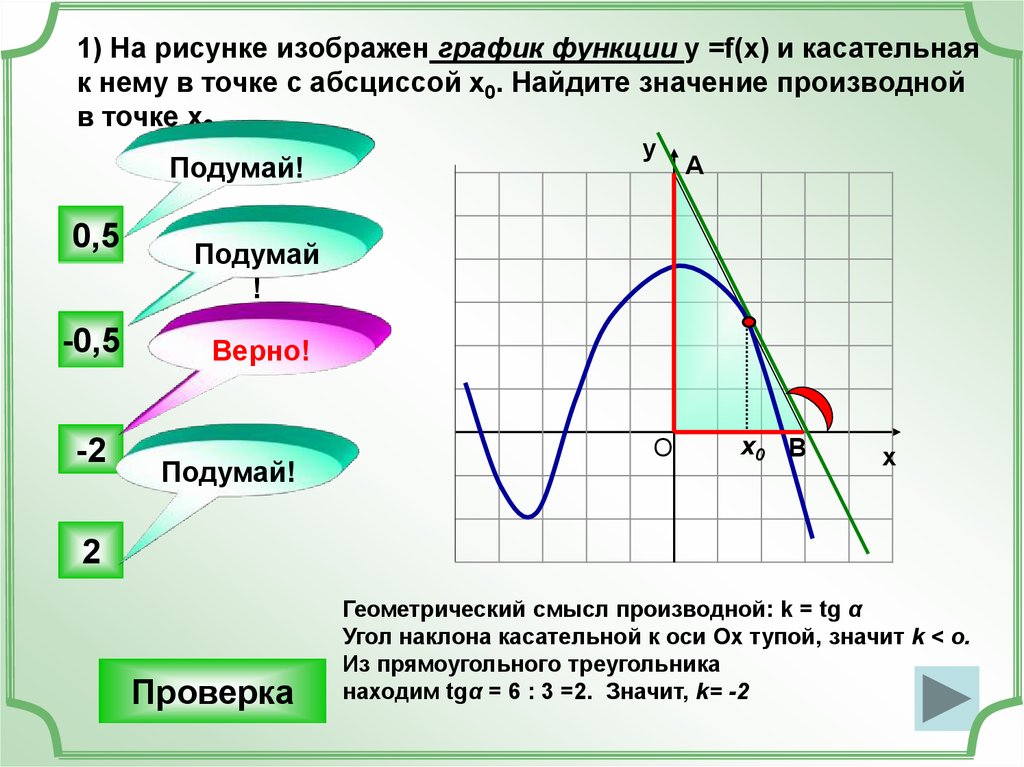
1) На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х0. Найдите значение производной
в точке х0.
Подумай!
-0,5
-2
А
Подумай
!
Верно!
Подумай!
О
0,5
y
х0 В
x
2
Проверка
Геометрический смысл производной: k = tg α
Угол наклона касательной к оси Ох тупой, значит k < o.
Из прямоугольного треугольника
находим tgα = 6 : 3 =2. Значит, k= -2

14.

2) Непрерывная функция у = f(x) задана на интервале (-6; 7).
На рисунке изображен ее график. Найдите количество точек, в
которых касательная к графику функции параллельна прямой
y = 6.
y
Верно!
3
.
y=6
Подумай!
5
Подумай!
-6
11
-4
Подумай!
Проверка
Точка излома. В этой
точке производная НЕ
существует!
О
8
y = f(x)
1,5
3
5
7
x

15.

Задачи на
определение
характеристик
функции по графику
её производной

16.

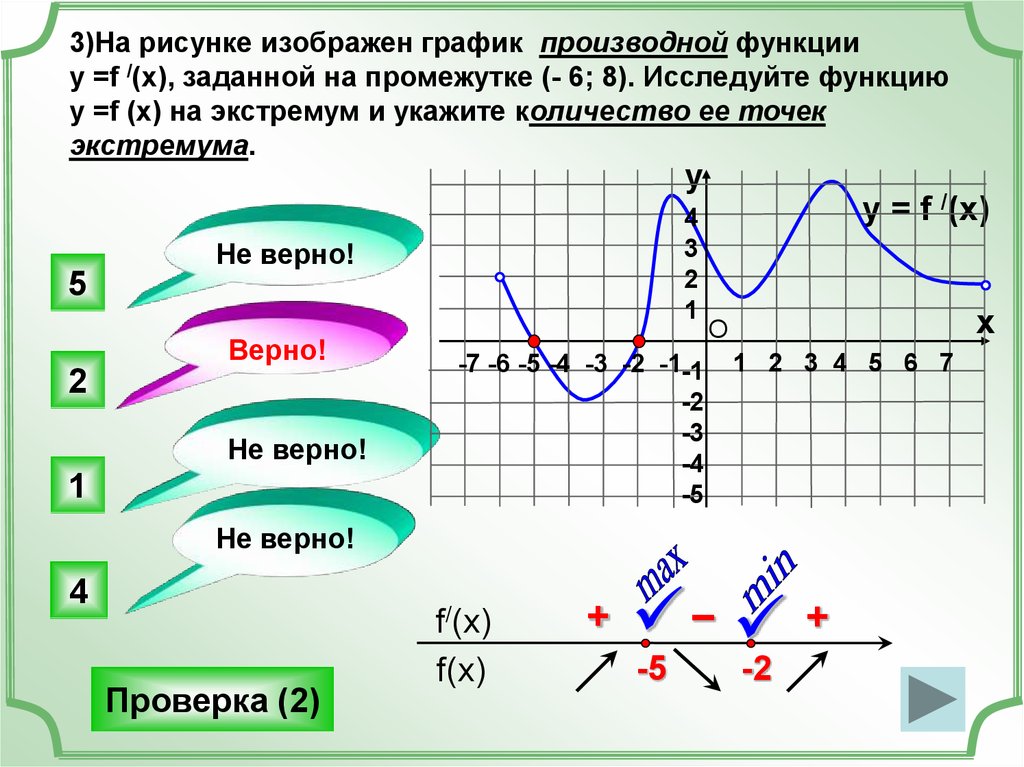
3)На рисунке изображен график производной функции
у =f /(x), заданной на промежутке (- 6; 8). Исследуйте функцию
у =f (x) на экстремум и укажите количество ее точек
экстремума.
y
4
3
2
1
Не верно!
5
Верно!
2
Не верно!
1
-7 -6 -5 -4 -3 -2 -1-1
-2
-3
-4
-5
y = f /(x)
x
О
1 2 3 4 5 6 7
Не верно!
4
Проверка (2)
f/(x)
f(x)
+
– +
-5
-2

17.

5) На рисунке изображен график производной функции,
заданной на промежутке [-5;5]. Исследуйте функцию на
монотонность и укажите наибольшую точку максимума .
y
Из двух точек максимума
наибольшая хmax = 3
Подумай!
y = f /(x)
5
+
Верно!
3
-
-4 -3 -2 -1-
-
+
О
+2
1
3
4
-
Подумай!
2
Подумай ! f/(x)
4
f(x)
-4
-2
-
+
0
-
3
+
4
+
5
х

18.

7) На рисунке изображен график производной функции.
Найдите длину промежутка возрастания этой функции.
y
ПОДУМАЙ!
2
ВЕРНО!
4
7
6
5
4
3
2
1
y = f /(x)
+
ПОДУМАЙ
-7 -6 -5 -4 -3 -2 -1 -1 О
!
3
ПОДУМАЙ!
5
Проверка
-2
-3
-4
-5
-6
-7
х
3

19.

6) На рисунке изображен график производной функции,
заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на
монотонность и укажите число промежутков убывания .
y
Подумай!
1
3
2
4
y = f /(x)
Верно!
+
О
-4 -3 -2 -1
Подумай!
-
1
2
+3
4
5 х
-
-
Подумай!
f/(x)
f(x)
-
+
-4
-2
+
0
4

20.

Задачи на
определение
характеристик
производной по
графику функции
.

21.

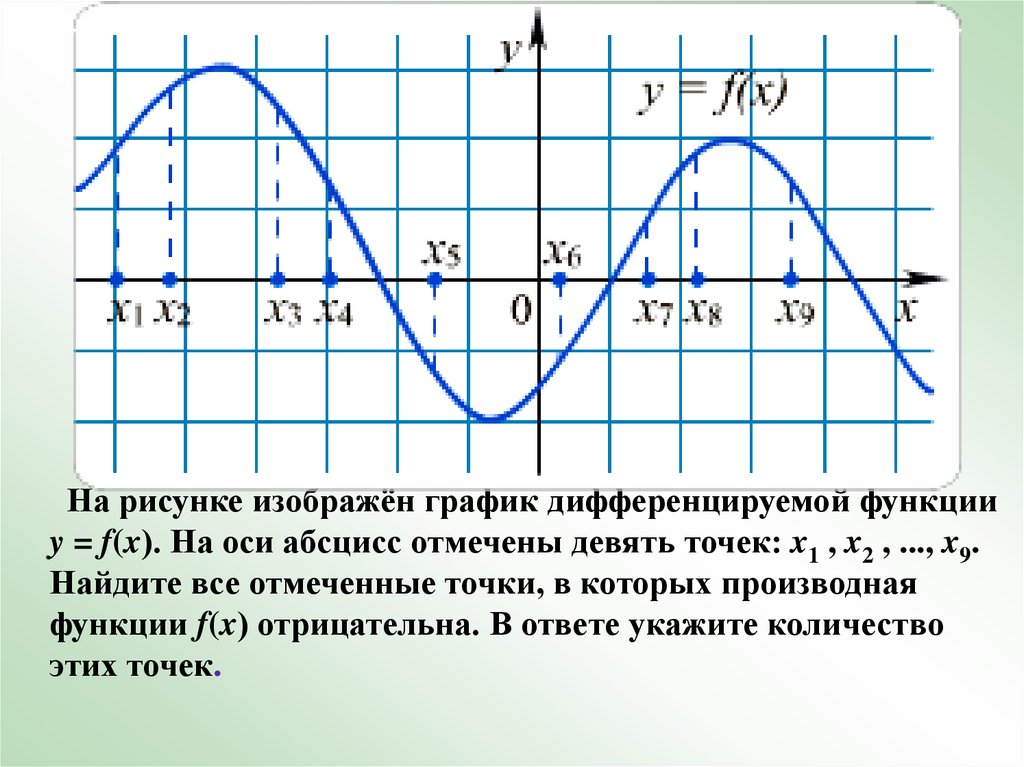
На рисунке изображён график дифференцируемой функции
y = f(x). На оси абсцисс отмечены девять точек: x1 , x2 , ..., x9.
Найдите все отмеченные точки, в которых производная
функции f(x) отрицательна. В ответе укажите количество
этих точек.

22.

На рисунке изображен график функции y = f (x),
определенной на интервале (a;b). Определите количество целых
точек, в которых производная функции положительна.
Решите самостоятельно!
a)
б)
Решение.
f ( x) 0, если f (x) возрастает.
Целые решения при :
Целые решения при :
х=-2; х=-1; х=5; х=6.
х=2; х=3; х=4; х=10; х=11.
Их количество равно 4.
Их количество равно 5.
Ответ: 4.
Ответ: 5.

23.

Задачи
на физический
смысл производной

24.

Ответ: 3
Ответ: 14

25. ЗАДАНИЕ № 12

Математика
профильный уровень
ЗАДАНИЕ № 12

26.

27.

28. Самостоятельная работа в парах

Задание № 12
Профильный уровень