Подготовка к ОГЭ: задача 13 (системы счисления)

1. Подготовка к ОГЭ: задача 13 (системы счисления)

Мочалова Марина Владимировна
Учитель информатики
ГБОУ лицей №144 Калининского района
г. Санкт-Петербург

2.

Содержание
1.Теория
2.Разбор решений задач
3.Задачи для самостоятельного решения
4.Источники

3.

Теория
Позиционные системы счисления
– что понимают под позиционными СС?
СС, в которых «вес» (значение) цифры зависит от ее места
(позиции) в изображении числа
– что понимают под p - основанием позиционной СС?
p – количество знаков, используемых для представления чисел,
а также «вес» разряда
– развернутая форма представления чисел в позиционных СС?
Ap=anpn + an-1pn-1 + . . . + a2p2 + a1p1 + a0p0
Ap – само число в СС с основанием p
ai – значащие цифры числа
n – число разрядов числа

4.

Теория
Позиционные системы счисления
– свернутая форма представления целых чисел в позиционных
СС?
A=anan-1 . . . a2a1a0
где an, an-1, . . . a2, a1, a0 - значащие цифры числа
– какой
формой записи чисел мы пользуемся в
повседневной жизни?
свернутой формой представления чисел (1945)

5.

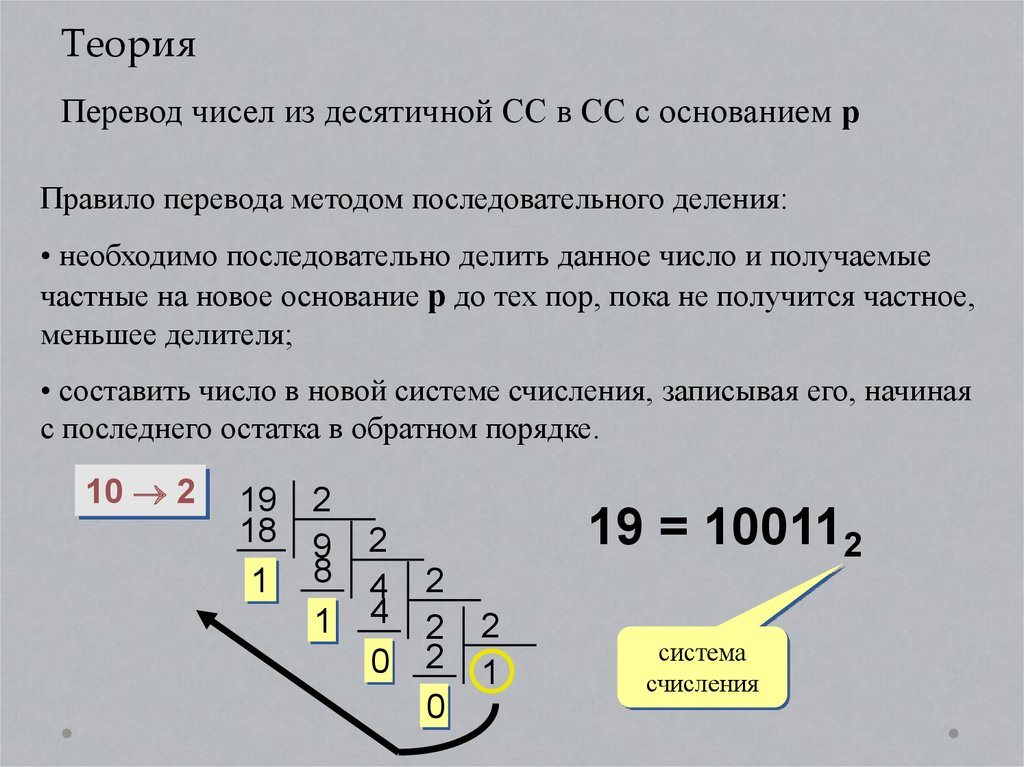
Теория
Перевод чисел из десятичной СС в СС с основанием р
Правило перевода методом последовательного деления:
• необходимо последовательно делить данное число и получаемые
частные на новое основание р до тех пор, пока не получится частное,
меньшее делителя;
• составить число в новой системе счисления, записывая его, начиная
с последнего остатка в обратном порядке.
10 2
19
18
1
2
9
8
1
2
4
4
0
19 = 100112
2
2
2
0
2
1
система
счисления

6.

Теория
Перевод чисел из позиционной СС с основанием р
в десятичную систему счисления
Правило перевода:
• представить число в развернутой форме;
• вычислить сумму ряда.
Полученный результат является значением числа в 10-ой СС.
Пример: число 32015 перевести в 10-ую СС
3 210
32015 =
3 · 53 + 2 · 52 + 0 · 51 + 1 · 50 =
= 3 · 125 + 2 · 25 + 1
= 426
32015 = 426

7.

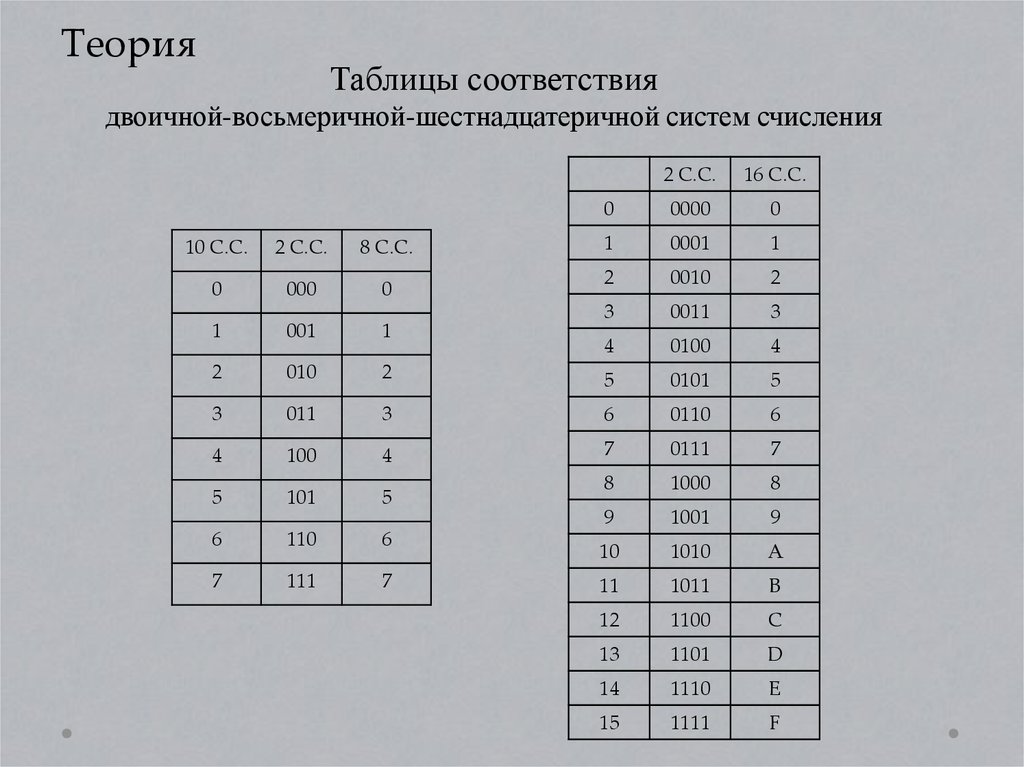
Теория
Таблицы соответствия
двоичной-восьмеричной-шестнадцатеричной систем счисления
10 С.С.
2 С.С.
8 С.С.
0
000
0
2 С.С.
16 С.С.
0
0000
0
1
0001
1
2
0010
2
3
0011
3
4
0100
4
1
001
1
2
010
2
5
0101
5
3
011
3
6
0110
6
4
100
4
7
0111
7
5
101
5
8
1000
8
9
1001
9
6
110
6
10
1010
A
7
111
7
11
1011
B
12
1100
C
13
1101
D
14
1110
E
15
1111
F

8.

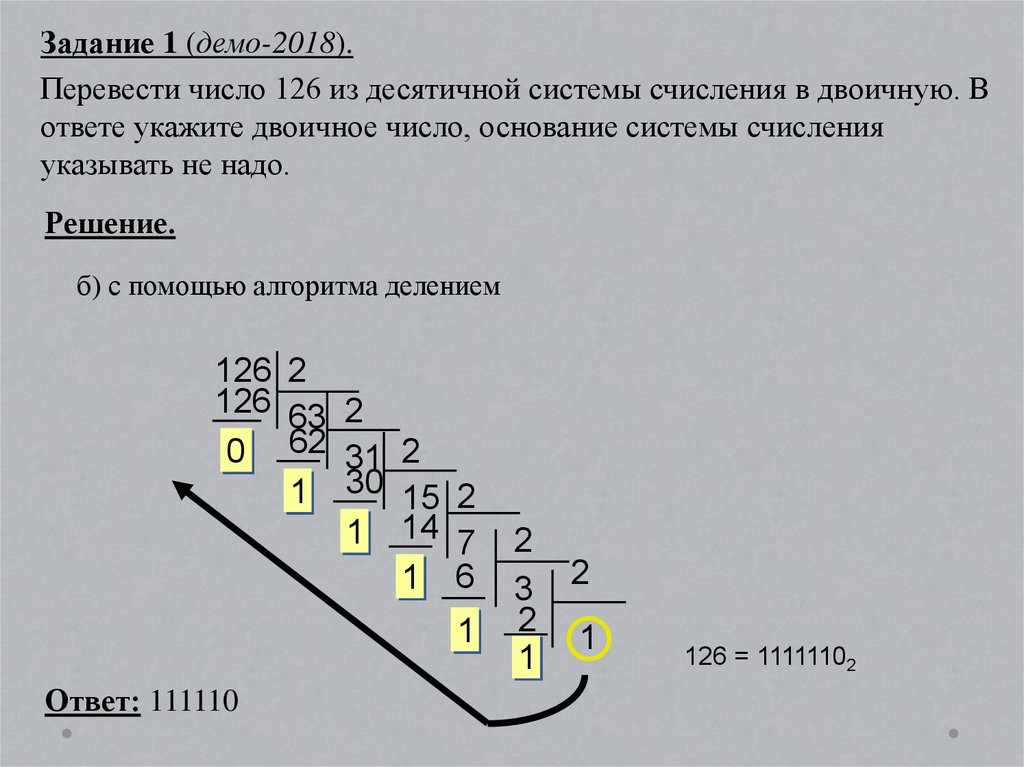
Задание 1 (демо-2018).
Перевести число 126 из десятичной системы счисления в двоичную. В
ответе укажите двоичное число, основание системы счисления
указывать не надо.
Решение.
а) методом разложения числа на степени основания 2.
Метод заключается в следующем: если число нечетное, раскладываем
его на сумму 1 и четной части, из которой выделяем степень двойки,
максимально к ней приближенную. Далее алгоритм повторяем.
Если исходное число четное, сразу выделяем степени двойки по
убыванию. Ответ записываем поразрядно, начиная со старшего. Если
очередная степень двойки отсутствует, в этом разряде пишем 0.
Метод удобен при небольших числах.
126 = 64 + 62 = 64 + 32 + 30 = 64 + 32 +16 + 14 = 64 + 32 +16 + 8 + 6 = = 64 +
32 +16 + 8 + 4 +2 = 26 + 25 + 24 + 23 + 22 +21
Ответ: 111110
126 = 11111102

9.

Задание 1 (демо-2018).
Перевести число 126 из десятичной системы счисления в двоичную. В
ответе укажите двоичное число, основание системы счисления
указывать не надо.
Решение.
б) с помощью алгоритма делением
126 2
126 63 2
0 62 31 2
1 30 15 2
1 14 7
1 6
1
Ответ: 111110
2
3 2
2
1
1
126 = 11111102

10.

Задание 2.
Представить в свернутой форме записи число
А9 = 7 · 95 + 3 · 94 + 6 · 92 + 9 1 + 2
Решение.
Задача не требует решения. Нужно записать значащие цифры
исходного числа, начиная со старшего разряда, при этом, если
очередной разряд отсутствует, то на этом месте пишем 0.
Ответ: А9 = 7306129
А = 3 · 102 + 1 · 101 + 7 · 100
Задание 3.
Представить число А = 317 в развернутой форме записи
Решение.
Так как в условии задания не указано основание системы счисления, то
считаем его равным 10. Представить число в развернутой форме означает
разложить его по базису (полезно надписать над значащими цифрами
числа степени, в которые возводится основание 10, начиная с младшего
210
разряда).
А = 317 = 3 · 102 + 1 · 101 + 7 · 100
Ответ: А = 3 · 102 + 1 · 101 + 7 · 100

11.

Задание 4.
Выстроить числа в порядке возрастания
А = 10213
В = 1115
С = 101012
D = 1219
Решение.
Как видно из условия, все числа даны в разных системах счисления.
Для решения задачи переведем их в десятичную систему счисления
(методом разложения по базису).
3 210
А = 10213 = 1 · 33 + 2 · 31 + 1 · 30 = 34
10
B = 1115 = 1 · 151 + 1 · 150 = 16
4 32 1 0
C = 101012 = 1 · 24 + 1 · 22 + 1 · 20 = 21
210
D = 1219 = 1 · 92 + 2 · 91 + 1 · 90 = 100
Ответ: B < C < A < D

12.

Задание 5.
Вычислить сумму чисел 10213 + 2105. Ответ представить в семеричной
системе счисления.
Решение.
Как видно из условия, все числа даны в разных системах счисления. Для
решения задачи переведем их в десятичную (методом разложения по
базису). Затем выполним сложение и результат переведем в семеричную
систему счисления (методом деления).
3 210
10213 = 1 · 33 + 2 · 31 + 1 · 30 = 34
21 0
2105 = 2 · 52 + 1 · 51 = 51
34 + 51 = 85
85 = 1517
Ответ: 1517

13.

Задание 6.
Было 53р груши. После того, как каждую разрезали пополам, стало 136
половинок. В системе счисления с каким основанием вели счет?
Решение.
Т.к. ответ дан в десятичной СС, определяем, сколько было целых груш?
Итого: 136 : 2 = 68 груш было.
а) решение методом анализа:
т.к. количество груш в СС с основанием р меньше, чем их число в
десятичной СС (68 = 53р), значит р > 10.
Проверяем числа ≥11. Находим: р = 13
б) с помощью вычислений:
Переводим 53р в десятичную СС и находим р:
53р = 5·р + 3
Ответ: 13
5р + 3 = 68
р = 13

14.

Задание 7.
Космонавты встретили инопланетянина, который свободно разговаривал на
земном языке. Выяснилось, что у гостя 13 сыновей и 23 дочери, а всего
детей – 102. Найдите, какой системой счисления пользовался гость?
Решение.
Для решения задачи переводим данные нам числа в десятичную систему
счисления и из полученного уравнения находим искомое р.
13р + 23р = 102р
(р + 3) + (2·р + 3) = р2 + 2
3р + 6 = р2 + 2
р2 – 3р – 4 = 0
(р – 4)·(р + 1) = 0
корень р1 = -1 – не имеет смысла (основание системы счисления
не может быть отрицательным числом)
р2 = 4
Ответ: гость пользовался четверичной системой счисления

15.

Задание 8.
В каких системах счисления перевод числа 37 оканчивается на 7?
Решение.
Анализируем исходное число. Оно должно оканчиваться на цифру 7.
Отсюда следует вывод: основанием системы счисления может быть
число 8 и более.
Окончание числа – это самый младший его разряд. Выделяем его:
37 = 30 + 7.
Число 30 кратно числам 3, 5, 6, 10, 15, 30 . Но системы счисления с
основаниями 3, 5, 6 не содержат цифру 7, поэтому не подходят.
Число 10 также не походит, так как по условию задачи число дано в
десятичной системе счисления.
Остаются значения р=15 и р=30.
Ответ: в 15-ричной и 30-ричной системах счисления

16.

Задание 9.
Вычислите значение суммы в троичной СС: 104 + 106 + 108 + 1012= ?
Ответ: 10103
Задание 10.
Троичным эквивалентом числа 600 является:
Ответ: 2110203
Задание 11.
Сколько единиц содержит двоичная запись числа 101?
Ответ: 5
Задание 12.
В системе с некоторым основанием число 17 записывается как 101.
Укажите это основание.
Ответ: 4

17.

Задание 13.
В коробке 31 шар. Из них 12 красных и 17 желтых. В какой системе счисления
такое возможно?
Ответ: в восьмеричной
Задание 14.
Даны 4 числа. Поставьте их в порядке убывания.
А = 3034 В = 1101012 С = 1356 D = 678
Ответ: CDBA
Задание 15.
Даны 4 числа, они записаны с использованием различных систем счисления.
Укажите среди этих чисел то, в двоичной записи которого содержится ровно
5 единиц. Если таких чисел несколько, укажите наибольшее из них.
1) 1510
Ответ: 3)
2) 778
3) 3458
4) FA16

18.

Задание 16.
Десятичное число 65 в некоторой системе счисления записывается как 230.
Определите основание системы счисления.
Ответ: 5
Задание 17 (ФИПИ, открытый банк заданий).
Сколько единиц в двоичной записи числа 519?
Ответ: 4
Задание 18.
Без перевода чисел в десятичную систему счисления определите, сколько
«1» содержится в двоичной сумме F816 + 738 ?
Ответ: 10

19.

Задание 19 (ФИПИ открытый банк заданий)
В системе счисления с некоторым основанием десятичное число 20
записывается как 110. Укажите это основание.
Ответ: 4
Задание 20.
Вычислите значение суммы в семеричной СС: 111102 + 11104 + 1106 + 108 = ?
Ответ: 3237
Задание 21.
Постройте числа в порядке убывания:
A=12304 B=1456 C= 4711 D=5313
Ответ: ADBC
Задание 22.
В каких системах счисления перевод числа 75 оканчивается на 9?
Ответ: в 11-ричной, 22-ричной, 33-ричной и 66-ричной системах
счисления

20.

Источники
• сайт К. Полякова
http://kpolyakov.spb.ru
• Е.М Зорина, М.В. Зорин. ОГЭ-2018. Информатика.
Тематические тренировочные задания. Москва. АСТ. 2017
• С.С. Крылов, Т.Е. Гурина ЕГЭ-2016 – типовые
экзаменационные варианты. Информатика и ИКТ. Москва.
Национальное образование. 2016
• В.Р. Лещинер. Информатика. ЕГЭ-2015. Типовые тестовые
задания. Москва. Издательство «Экзамен». 2015