Похожие презентации:
Средние статистические показатели
1.
Средние статистическиепоказатели
2. Статистический показатель -
Статистический показатель это объективная, обобщающая количественнаяхарактеристика явления или процесса в его
качественном определении, т.е. с социальноэкономическим содержанием, в конкретных
условиях места и времени.
3. Статистические показатели по форме выражения:
выраженияАбсолютные
Относительные
Средние
4. Средним показателем
называется величина, котораявыражает типичные черты и дает
обобщающую количественную
характеристику социальноэкономического явления по одному
варьирующему признаку
5. Виды средних показателей:
1.Средняя арифметическая
2.
Средняя гармоническая
3.
Средняя хронологическая
4.
Средняя геометрическая
5.
Средняя квадратическая (степенная средняя)
6. Исходное соотношение средней (ИСС)
ИСС=Суммарные значение или
объем осредняемого признака
Количество элементов по
осредняемому признаку
7. Средняя арифметическая
простаявзвешенная
8. Средняя Арифметическая простая
9. По результатам сдачи экзаменов по Теории статистики рассчитайте средний балл:
ИвановСмирнов
Сотникова
Петров
Рыбаков
Курочкин
Селезнев
5
4
3
4
3
5
5
10.
су
м
а
в
с
е
х
п
о
л
ч
е
н
ы
о
ц
н
к
И
С
итдв
11.
54
3
4
3
5
X
7 4,1
12. Средняя арифметическая взвешенная
fXx
i
Средняя арифметическая взвешенная
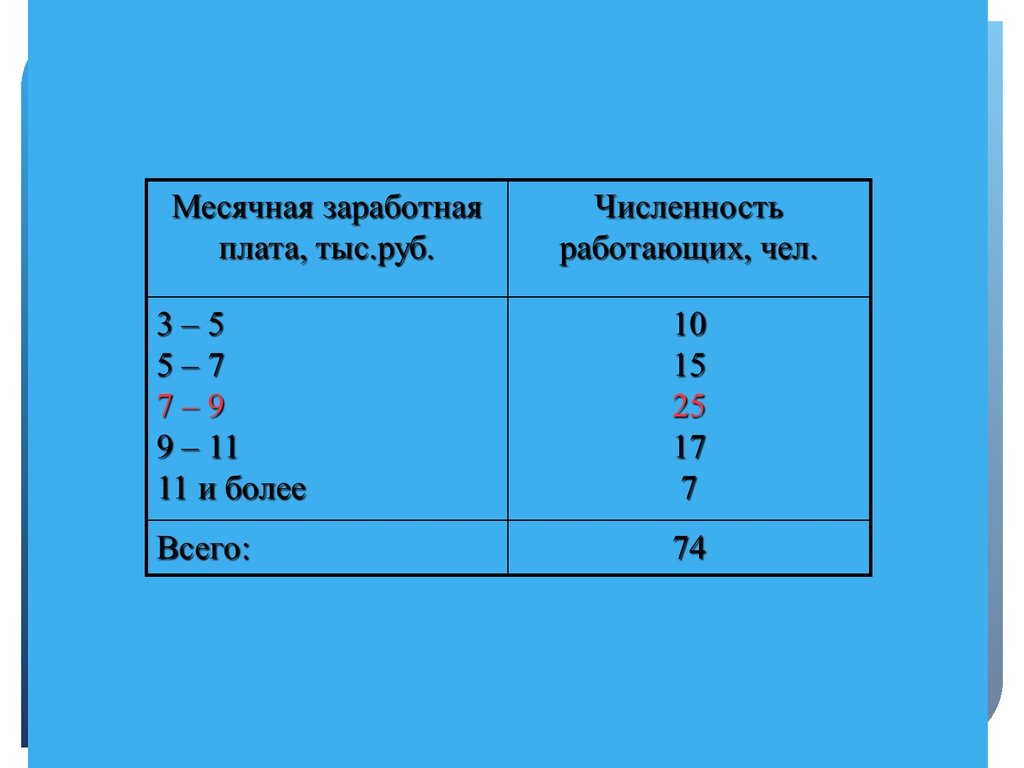
13. По данным о заработной плате рабочих промышленного предприятия рассчитайте среднюю заработную плату:
Месячнаязаработная плата,
тыс.руб.
Численность
работающих,
чел.
3–5
5–7
7–9
9 – 11
11 и более
10
15
25
17
7
Всего:
74
14.
фо
н
д
з
а
р
б
о
т
н
й
п
л
ы
И
С
чи
счи
х
15.
X175 8 275 7.9т
4
1
0
6
ы
сруб.
16. Средняя гармоническая:
простаявзвешенная
17. Средняя гармоническая простая:
nX
1
x
Средняя гармоническая простая:
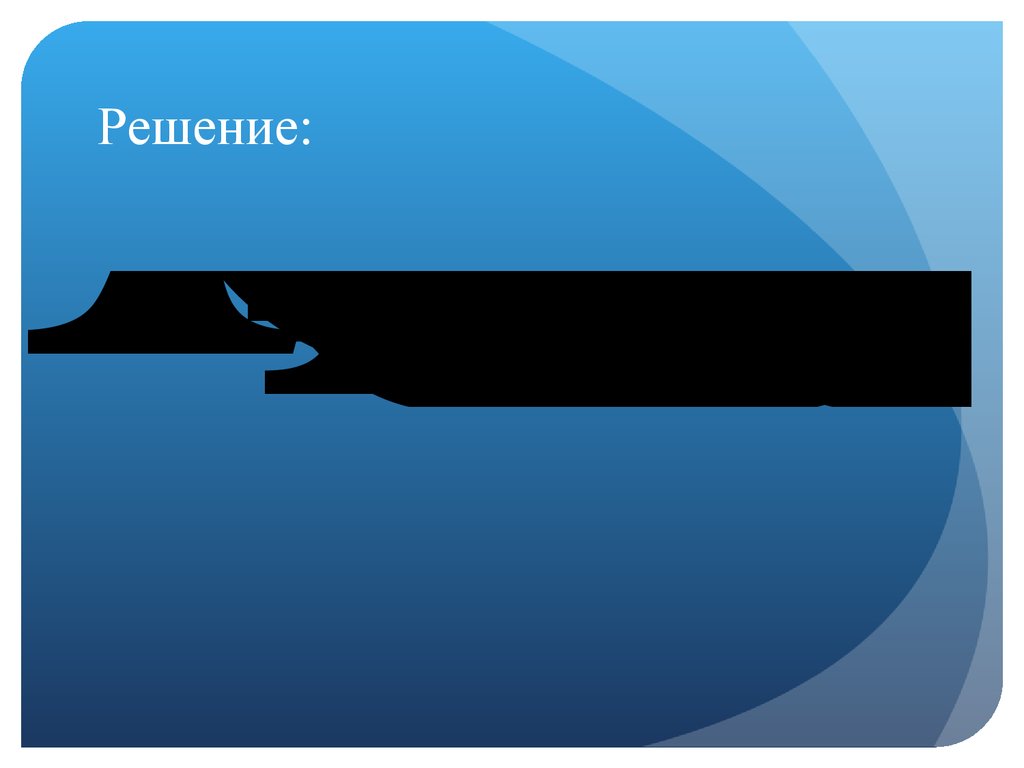
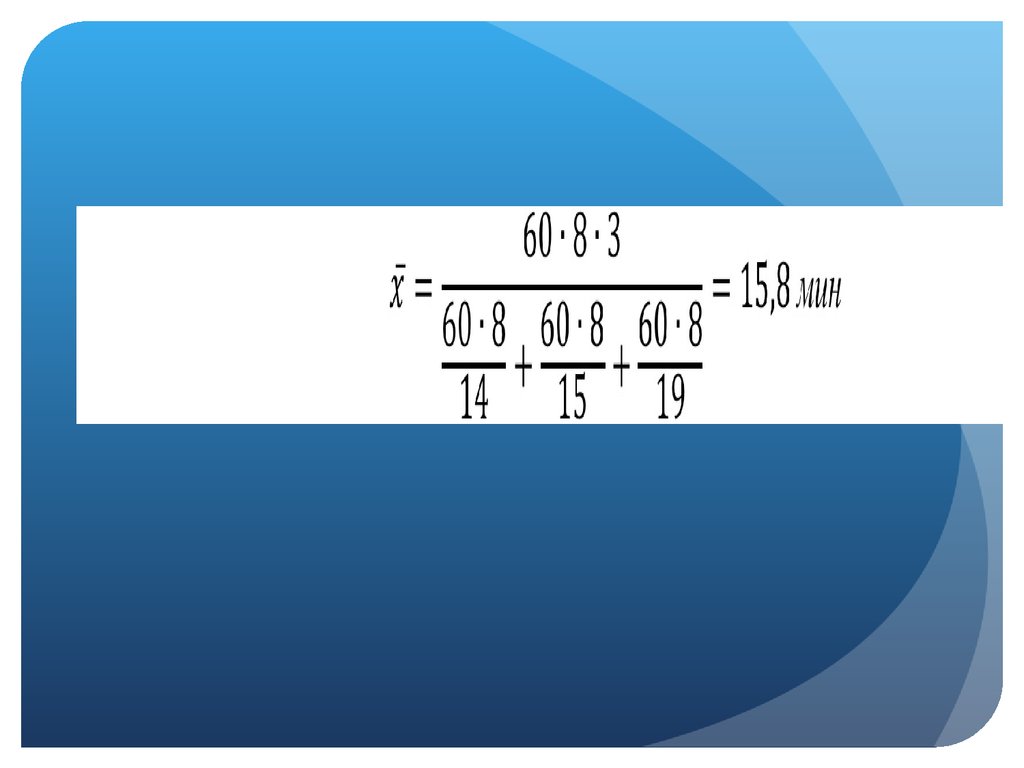
18. Например:
В отделе заказов торговой фирмы занято трое работников,имеющих 8-часовой рабочий день. Первый работник на
оформление одного заказа в среднем затрачивает 14 мин.,
второй - 15 мин., третий - 19 мин. Определите средние
затраты времени на 1 заказ в целом по отделу.
19. Решение:
об
щ
е
к
о
л
и
ч
е
с
т
в
о
р
а
б
о
т
н
г
о
в
р
е
м
н
и
И
С ы
плеы
хзак
Решение:
20.
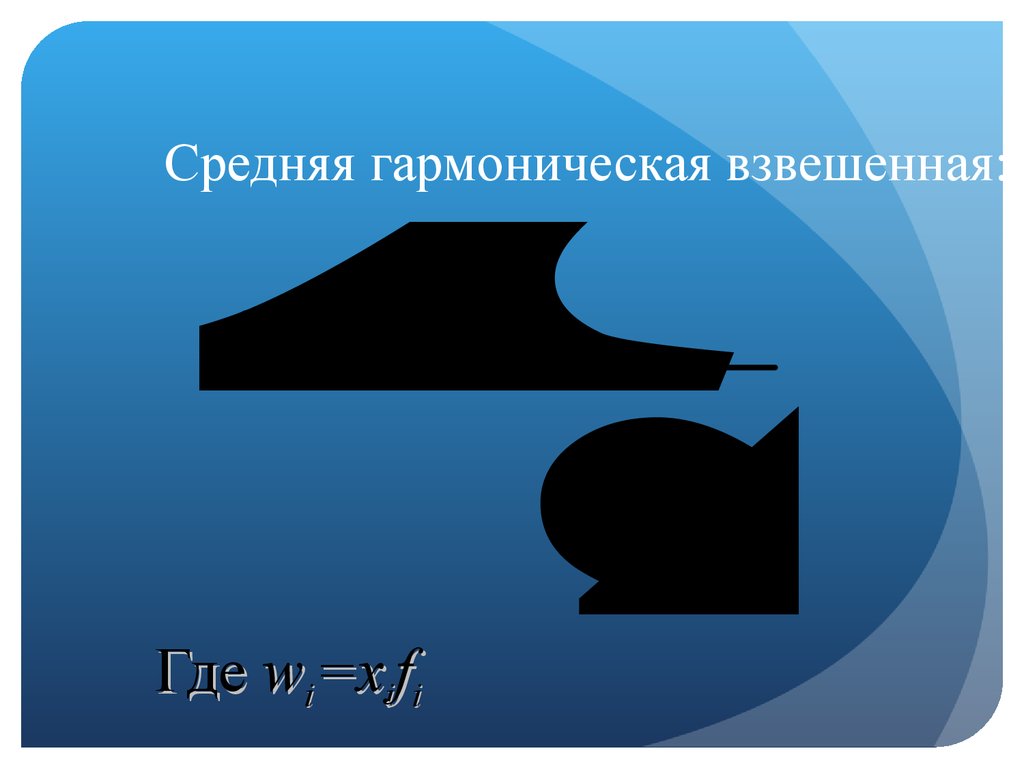
21. Средняя гармоническая взвешенная:
wi
X
x
Средняя гармоническая взвешенная:
Где
Где wi=xifi
22. Имеются следующие данные об урожайности зерновых культур в фермерских хозяйствах:
№ участкаВаловой
сбор, тыс.т
Урожайность,
ц/га
1
2
3
15 000
16 000
13 000
13
12
10
Рассчитайте среднюю урожайность
зерновых по фермерскому хозяйству
23.
Ва
л
о
в
й
с
б
о
р
И
С
П
сены
плщ
ади
24.
15
0
1
6
0
1
3
0
X/
32 1,6цга
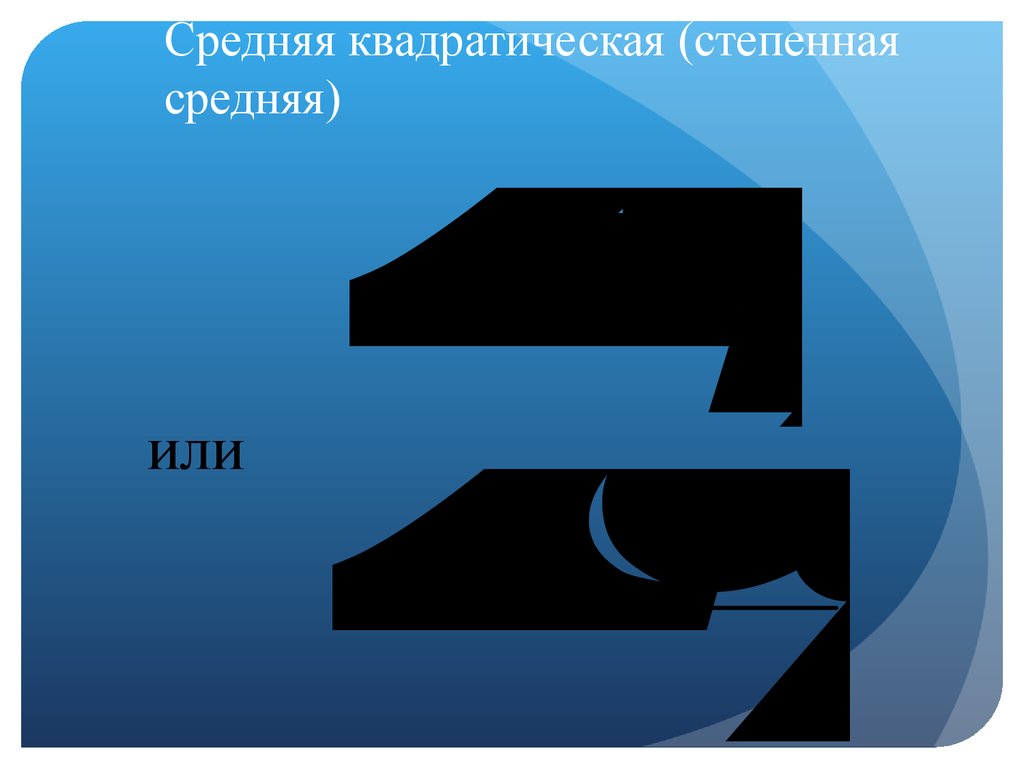
25. Средняя квадратическая (степенная средняя)
xX
nf
2
i
2
n
ni
Средняя квадратическая (степенная
средняя)
или
26. Средняя хронологическая
Простаявзвешенная
27. Средняя хронологическая простая
11
y
y
.
y
y
1
2
n
1
n
2
2
y
n
-1
Средняя хронологическая
простая
28.
( y1 2) t1(2
y2t 3) t2
.
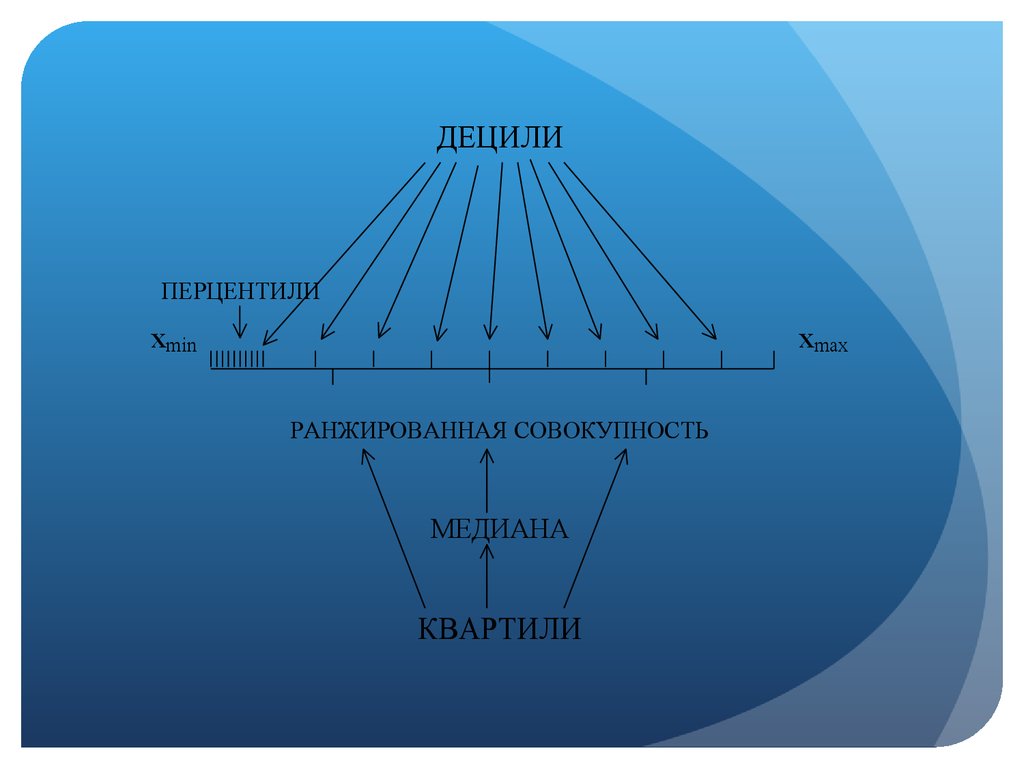
29. Структурные средние
МодаМедиана
Квартили
Децили
перцили
30.
Мода – это значение признака,которое наиболее часто
встречается в совокупности
31.
1. Если исходные данные не сгруппированы, томодальным будет называться значение признака,
наиболее часто встречающееся в совокупности
32. Например:
Результаты сдачи экзамена по статистики одной изстуденческих групп:
5,2,4,2,3,2,2,2
Мо=2
33.
2. Если исходные данные представлены ввиде дискретного вариационного ряда
распределения, то модальным будет
называться значение признака с
максимальной частотой.
34.
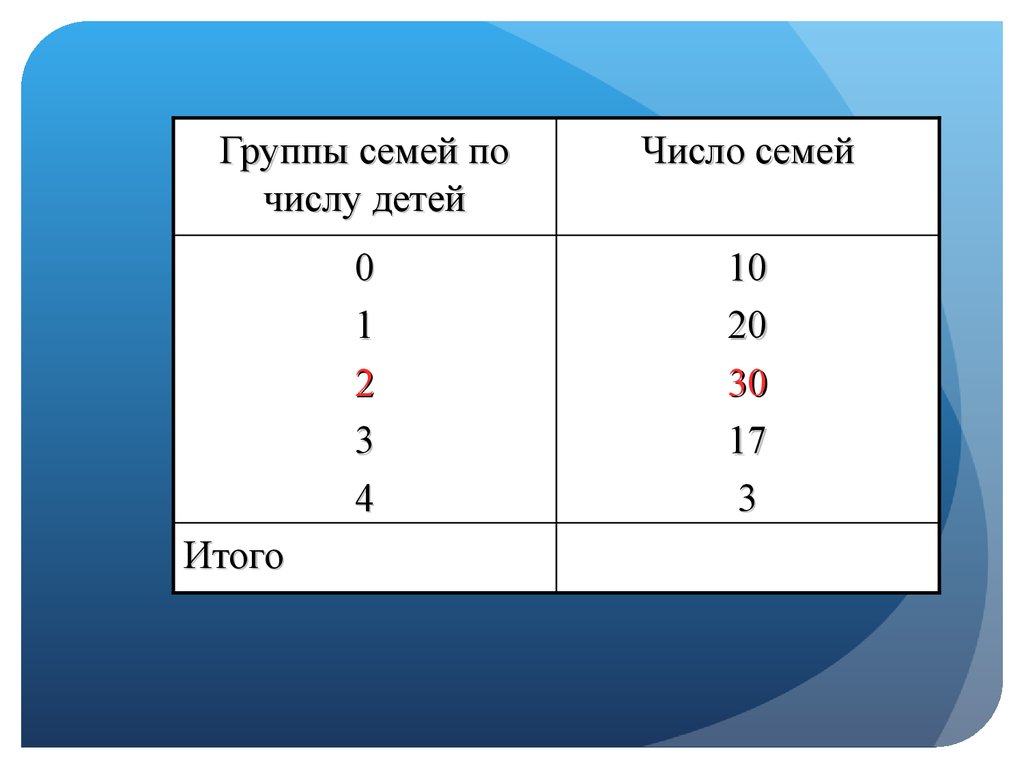
Группы семей почислу детей
Число семей
0
1
2
3
4
10
20
30
17
3
Итого
35. Мода
fM
o
M
o
1
M
o X
h2fMo 1
0
3. Если исходные данные представлены в
виде интервального вариационного ряда
распределения
36.
37.
38.
Медиана – это значениепризнака, которое стоит в
середине упорядоченной
совокупности
39.
1. Если исходные данные не сгруппированы ипредставлены в виде числовой последовательности,
то:
- Если нечетное количество единиц совокупности, то
медианой будет называться значение стоящее в
середине упорядоченной совокупности
- Если четное количество единиц совокупности, то
медиана определяется как среднее значение из двух в
середине стоящих значений упорядоченной
совокупности
40. Например:
Результаты сдачи экзамена по статистики одной изстуденческих групп:
5,2,4,2,3,2,2,2,5
1.Необходимо упорядочить совокупность
222223455
Ме=2
41. Например:
Результаты сдачи экзамена по статистики одной изстуденческих групп:
5,2,4,2,3,2,2,2,5,5
1.Необходимо упорядочить совокупность
22222 34555
Ме=2,5
42.
2. Если исходные данные представлены в виде дискретноговариационного ряда распределения, то
медианным называется значение, у которого накопленная
частота первой превысит половину суммы частот
43.
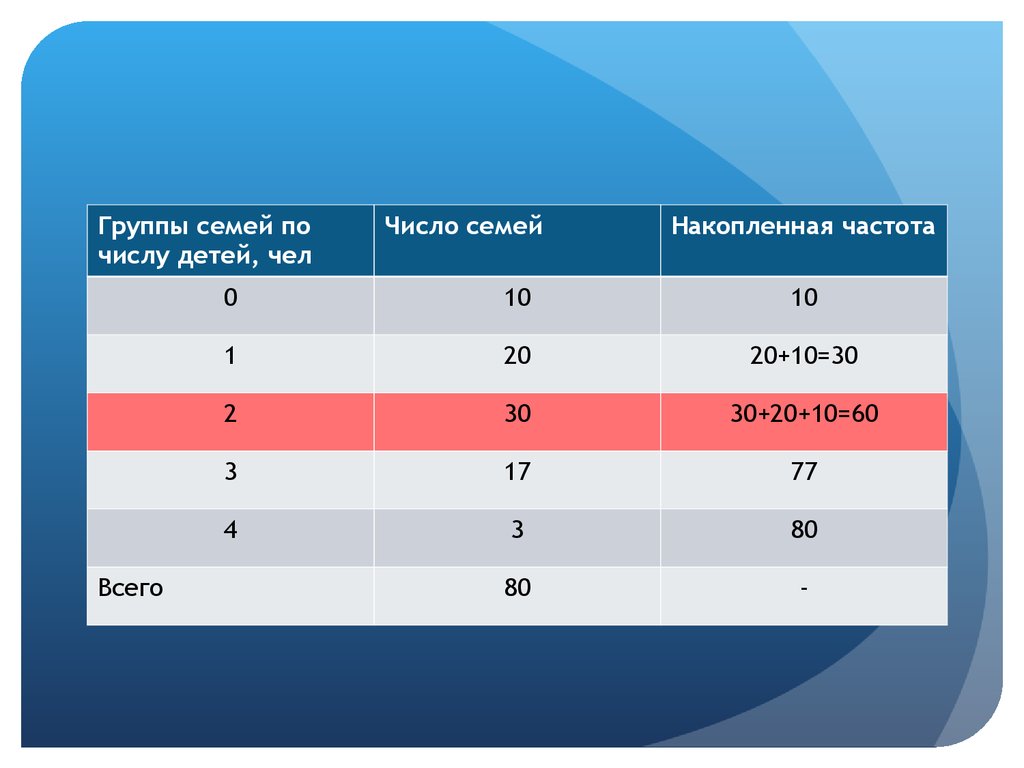
Группы семей почислу детей, чел
Всего
Число семей
Накопленная частота
0
10
10
1
20
20+10=30
2
30
30+20+10=60
3
17
77
4
3
80
80
-
44.
1H
f
M
e
1
2
M
e
X
h
0M
e
3. Если исходные данные представлены в виде интервального
вариационного ряда распределения
45.
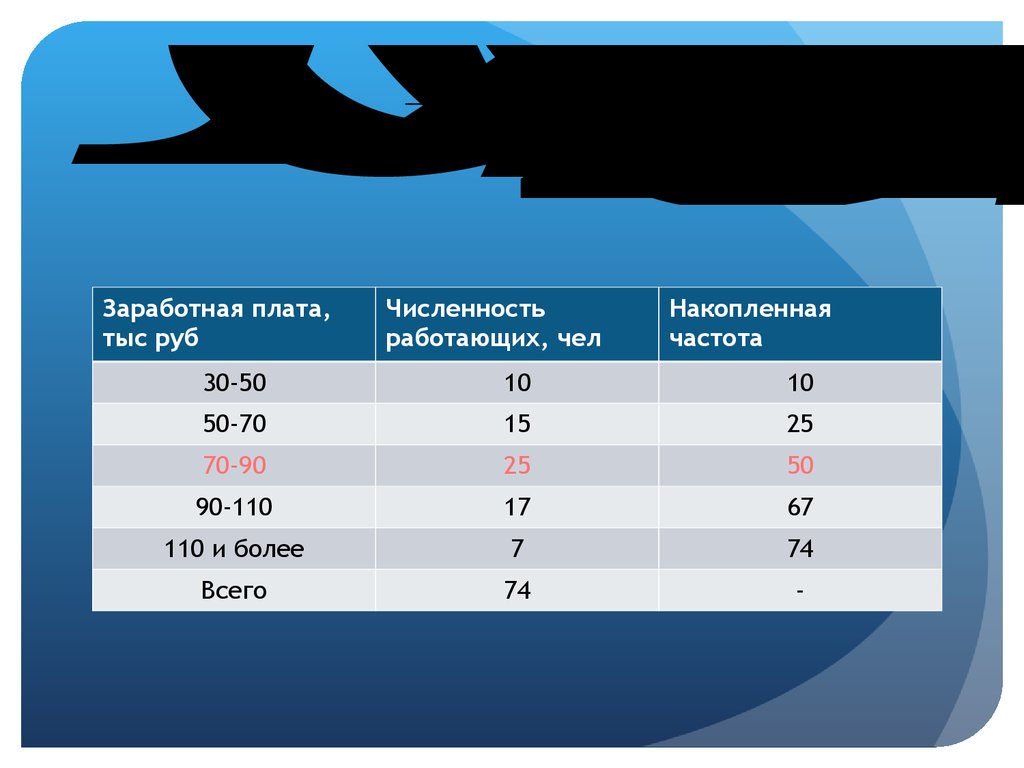
Месячнаязаработная
плата,
тыс.руб.
30 – 50
50 – 70
70 – 90
90 – 110
110 и более
Всего:
Численность
работающих,
чел.
10
15
25
17
7
74
46.
17
4
2
5
2
M
e
7
0
0
7
9
,6
т
ы
с
.ч
е
л
Заработная плата,
тыс руб
Численность
работающих, чел
Накопленная
частота
30-50
10
10
50-70
15
25
70-90
25
50
90-110
17
67
110 и более
7
74
Всего
74
-
47.
ДЕЦИЛИПЕРЦЕНТИЛИ
xmin
xmax
РАНЖИРОВАННАЯ СОВОКУПНОСТЬ
МЕДИАНА
КВАРТИЛИ
48.
Квартили – это значениепризнака, которое делят
совокупность на четыре
равные части
49.
1. Если исходные данные не сгруппированы ипредставлены в виде числовой последовательности,
то первой квартилей будет называться значение
отделяющие ¼ упорядоченной совокупности. Третей
квартилей будет называться значение признака
отделяющее ¾ упорядоченной совокупности.
50.
2. Если исходные данные представлены в виде дискретноговариационного ряда распределения, то
Первым квартильным называется значение, у которого
накопленная частота первой превысит ¼ суммы частот.
Третим квартильным называется значение, у которого
накопленная частота первой превысит ¾ суммы частот.
51.
1H
f
Q
1
1
4
Q
X
h
1
0
Q
1
3
H
f
Q
1
3
4
Q
X
h
3
0Q
3
. Если исходные данные представлены в виде
интервального вариационного ряда распределения
52.
Децили – это значениепризнака, которое делят
совокупность на десять
равных частей
53.
1H
f
d
1
1
0
d
X
h
1
0
d
1
2
H
f
d
1
2
1
2
0
f
d
2
3
H
d
1
3
0
d
X
h
3
0d
3






























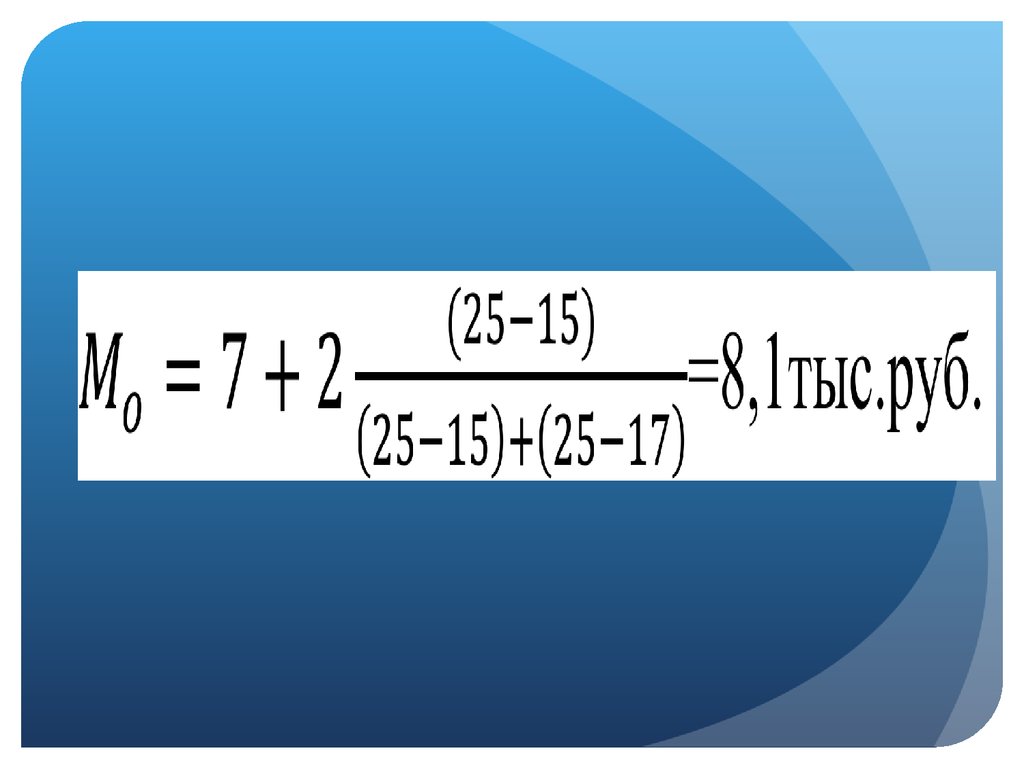













 Образование
Образование Социология
Социология








