Похожие презентации:
Модификации ВР. Изменение способа определения шага. Изменение способа вычисления
1. Модификации ВР
Корлякова М.О.2019
2. Методы
Изменение способа определения шагаИзменение способа вычисления
3. Изменение способа определения шага
Определять скорость обучения отдельно длякаждого элемента W.
Изменять скорость обучения для каждой
итерации.
Если производная функции стоимости имеет
постоянный знак для нескольких итераций, то скорость
обучения растет
Если производная функции стоимости показывает
изменение знак для нескольких итераций, то скорость
обучения растет
Вносить импульсные вариации в скорость
обучения.
4. Изменение способа вычисления
Изменение способавычисления
Градиентный спуск
Методы сопряженных градиентов.
Квази-Ньютоновские методы.
Метод стохастиеского градиента
5. Градиентный спуск
ff T
, ,
) частных
Вектор f (
x1
xn
производных функции f ( X ) f ( x1 , x2 ,..., xn )
Задает направление наискорейшего
возрастания этой функции
E (t )
wij (t 1) wij (t )
wij (t )
6. Метод сопряженных градиентов
Задача минимизации квадратичной функции.Функцию стоимости аппроксимируем
квадратичной функцией
f(w)=1/2 WT H W - Eav(W)/ W W + c
В качестве направления наискорейшего спуска
выбираем резидуальную ошибку r(n) – ошибка
нахождения минимума
Не использует Гессиан, но его приближение
7. Нелинейный алгоритм сопряжен градиентов
1.2.
3.
Инициализация
Вычисления
W(0) по ВР находим градиент g(0)
S(0)=r(0)=-g(0) (r(0) – резидуальная ошибка)
Для шага n - линейный поиск параметра (n)
Находится группа (которая является нетривиальным
интервалом), гарантированно содержащая минимум.
Разделение на подгруппы меньшего размера
8. Нелинейный алгоритм сопряжен градиентов
Ошибка r(n)<e_max(n), если да, тозакончить обучение. e_max(n)=r(0)/10000
5. W(n+1)=W(n)+ (n) s(n)
6. По ВР находим g(n+1)
7. r(n+1)=- g(n+1)
8. Вычисляем b по Полаку-Рибьеру
b(n+1)=max{0, (rT(n+1)(r(n+1)- r(n)))/(rT(n) r(n))}
9. Изменяем значение направления
10. s(n+1)=r(n+1)+b(n+1) s(n)
11. n=n+1 и к 3.
4.
9. Метод Ньютона
Формула ньютонаГессиан функции ошибки
10. LM
W= -(JT J +I*M)-1 JT EH JT J
J- Якобиан
g= JT E
11. BFGS
W= - H-1g(n)s(n)P(n)=-g(n)
s(n)=s(n-1)+u(n)
V(n)=W(n+1)-W(n)
Y(n)=g(n+1)-g(n)
S(n+1)V(n)=Y(n)
Broyden-Fletcher-Goldfarb-Shano
P(n+1)=-g(n) +[(V(n)* g(n+1))*s(n)/(Y(n)*s(n))]
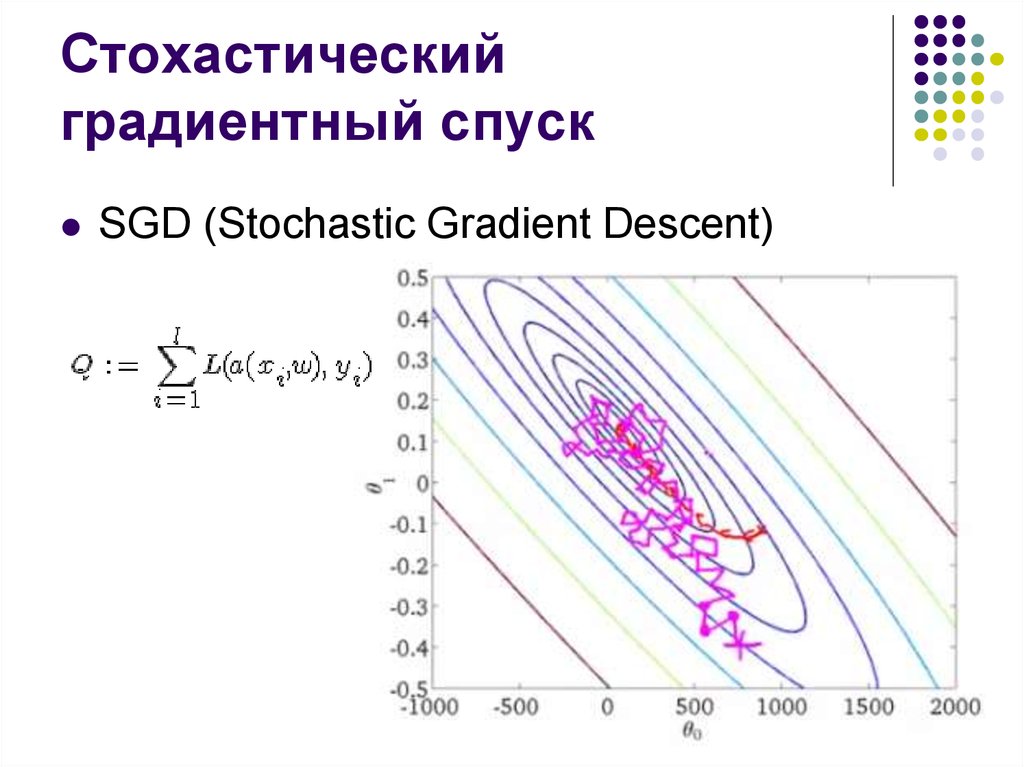
12. Стохастический градиентный спуск
SGD (Stochastic Gradient Descent)13. Стохастический градиентный спуск
1.Текущий шаг
Выбрать объект xi из (например, случайным
образом);
Вычислить выходное значение алгоритма и
ошибку;
Сделать шаг градиентного спуска;
Оценить значение функционала;
2.
Пока значение не стабилизируется и/или
веса не перестанут изменяться.
14. Изменение весов
2 класса14
12
10
8
6
4
2
0
-2
-2
0
2
4
6
8
10
12
14
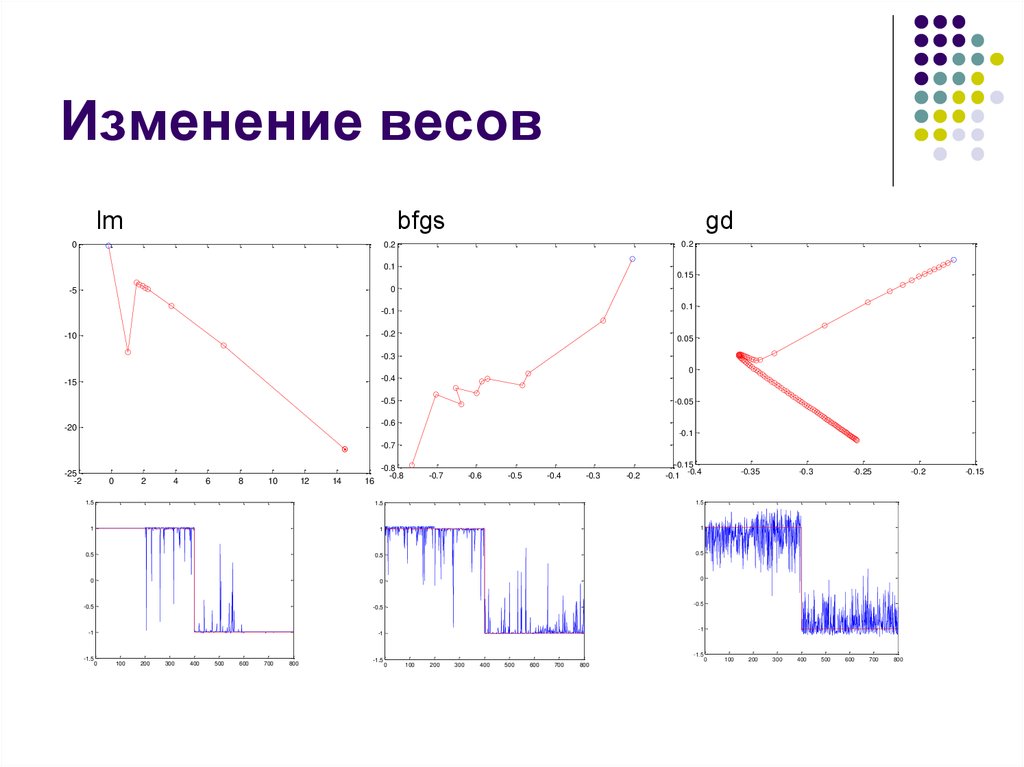
15. Изменение весов
lmbfgs
gd
0.2
0.2
0
0.1
0.15
0
-5
0.1
-0.1
-0.2
-10
0.05
-0.3
0
-0.4
-15
-0.5
-0.05
-0.6
-20
-0.1
-0.7
-25
-2
0
2
4
6
8
10
12
14
16
-0.8
-0.8
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.15
-0.1 -0.4
1.5
1.5
1.5
1
1
1
0.5
0.5
0.5
0
0
0
-0.5
-0.5
-1
-1
-1.5
0
100
200
300
400
500
600
700
800
-1.5
-0.35
-0.3
-0.25
-0.2
-0.5
-1
-1.5
0
100
200
300
400
500
600
700
800
0
100
200
300
400
500
600
700
800
-0.15














 Программирование
Программирование








