Силы, действующие на шейки коленчатого вала. Лекция №4

1. ТЕМА №3 «СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШЕЙКИ КОЛЕННЧАТОГО ВАЛА»

РАССМАТРИВАЕМЫЕ ВОПРОСЫ:
1. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ
2. СИЛЫ, НАГРУЖАЮЩИЕ КОРЕННЫЕ ШЕЙКИ
3. ПРИМЕР ПОСТРОЕНИЯ ДИАГРАММЫ НАГРУЗКИ НА
КОРЕННУЮ ШЕЙКУ
4. ТЕОРЕТИЧЕСКАЯ ДИАГРАММА ИЗНОСА ШЕЕК ВАЛА

2. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ

S
ω
Кrш
На шатунную шейку кривошипа
действует сила S’, направленная вдоль
оси шатуна, которая представляет
собой составляющую силы РΣ , а также
центробежная сила Кrш, действующая
по радиусу кривошипа и возникающая
от вращения части массы шатуна,
отнесенной к оси кривошипной
головки.

3. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ

β lш
K
T
φ+β К
rш
ω
φ
K
Rшш
T
S’
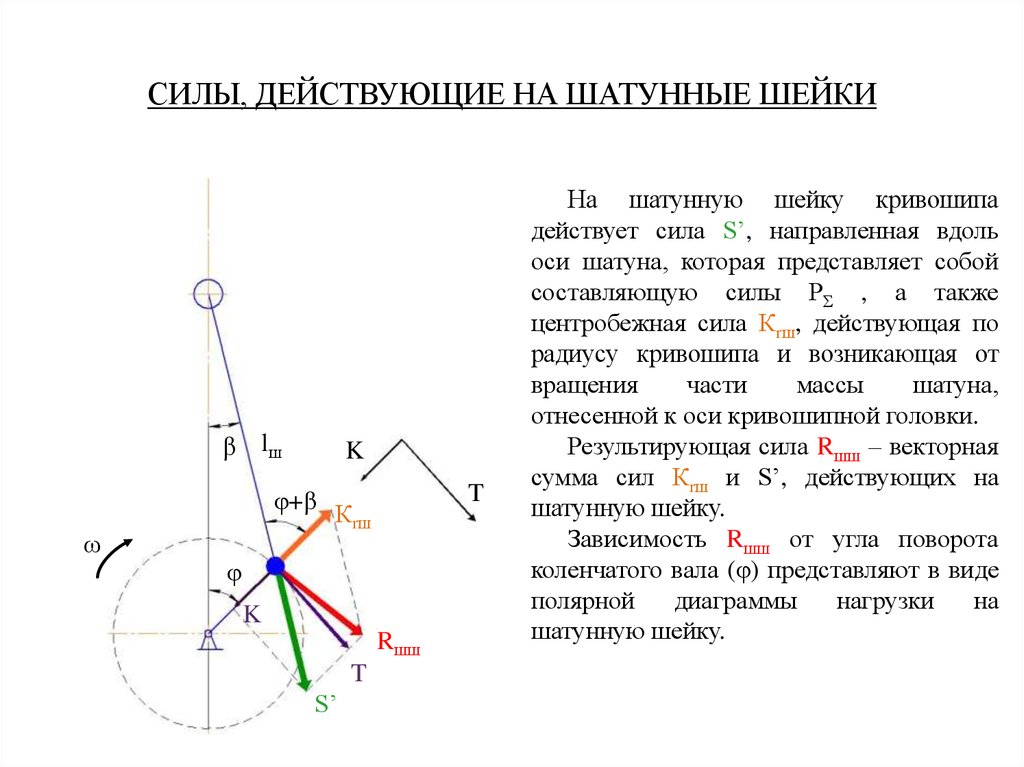
На шатунную шейку кривошипа
действует сила S’, направленная вдоль
оси шатуна, которая представляет собой
составляющую силы РΣ , а также
центробежная сила Кrш, действующая по
радиусу кривошипа и возникающая от
вращения
части
массы
шатуна,
отнесенной к оси кривошипной головки.
Результирующая сила Rшш – векторная
сумма сил Кrш и S’, действующих на
шатунную шейку.
Зависимость Rшш от угла поворота
коленчатого вала (φ) представляют в виде
полярной
диаграммы
нагрузки
на
шатунную шейку.

4. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ

-ω
-К
φ+β
Кrш
Rшш
φ
0
+К
S’
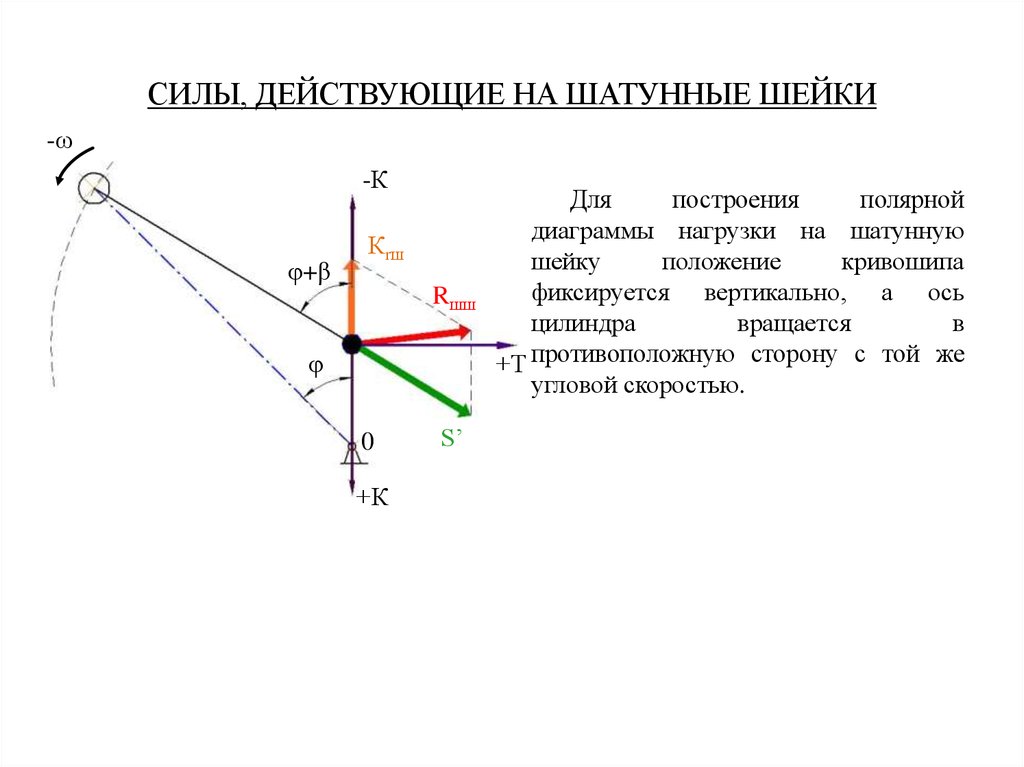
Для
построения
полярной
диаграммы нагрузки на шатунную
шейку
положение
кривошипа
фиксируется вертикально, а ось
цилиндра
вращается
в
+Т противоположную сторону с той же
угловой скоростью.

5. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ

-ω
-К
φ+β
Кrш
Rшш
S’
φ
+К
Для
построения
полярной
диаграммы нагрузки на шатунную
шейку
положение
кривошипа
фиксируется вертикально, а ось
цилиндра
вращается
в
+Т противоположную сторону с той же
угловой скоростью.
Так
как
при
неподвижном
кривошипе ориентация сил К, Т и Кrш
однозначно и просто определяется, то
процесс построения диаграммы сил
Rшш значительно упрощается.

6. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ

φ+β
Sφ’
-Т
-К
Кφ
Rшш(φ)
Кrш
0ш
+К
+Т
Принцип
построения
полярной
диаграммы нагрузки на шатунную шейку
1. В прямоугольных координатах из
полюса О для каждого угла по значениям
сил К и Т строится сила S’.
2. К точке О вдоль оси К прикладывают
вектор центробежной силы Кrш , величина
которого постоянна и направлена по
радиусу кривошипа.
3. Сила проведенная из точки Ош ,
представляющей начало вектора Кrш , в
точку соответствующую концу вектора S’
даст результирующую силу Rшш .

7.

СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ
-К
К
Т
φ
+Т
-Т
0°
180°
360°
540°
720°
+К
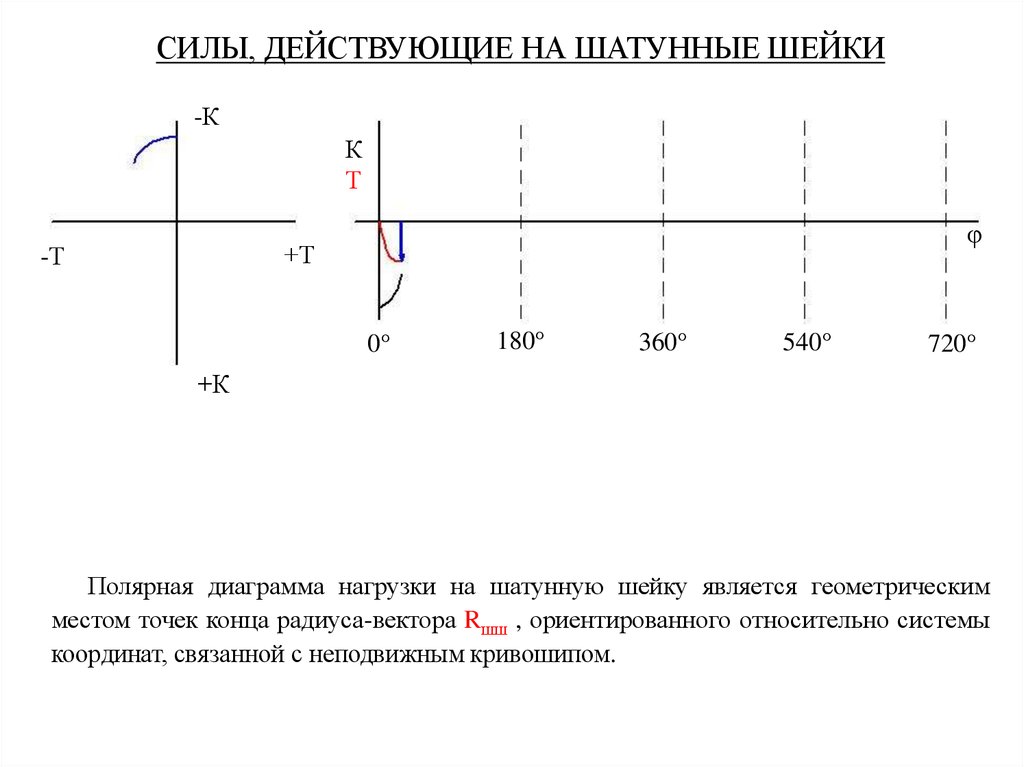
Полярная диаграмма нагрузки на шатунную шейку является геометрическим
местом точек конца радиуса-вектора Rшш , ориентированного относительно системы
координат, связанной с неподвижным кривошипом.

8.

СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ
-К
К
Т
φ
+Т
-Т
0°
180°
360°
540°
720°
+К
Полярная диаграмма нагрузки на шатунную шейку является геометрическим
местом точек конца радиуса-вектора Rшш , ориентированного относительно системы
координат, связанной с неподвижным кривошипом.

9.

СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ
-К
К
Т
φ
+Т
-Т
0
0°
180°
360°
540°
720°
+К
Полярная диаграмма нагрузки на шатунную шейку является геометрическим
местом точек конца радиуса-вектора Rшш , ориентированного относительно системы
координат, связанной с неподвижным кривошипом.

10.

СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ
-К
К
Т
φ
+Т
-Т
0
0°
180°
360°
540°
720°
+К
Полярная диаграмма нагрузки на шатунную шейку является геометрическим
местом точек конца радиуса-вектора Rшш , ориентированного относительно системы
координат, связанной с неподвижным кривошипом.

11.

СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ
-К
К
Т
φ
+Т
-Т
0
0°
180°
360°
540°
720°
+К
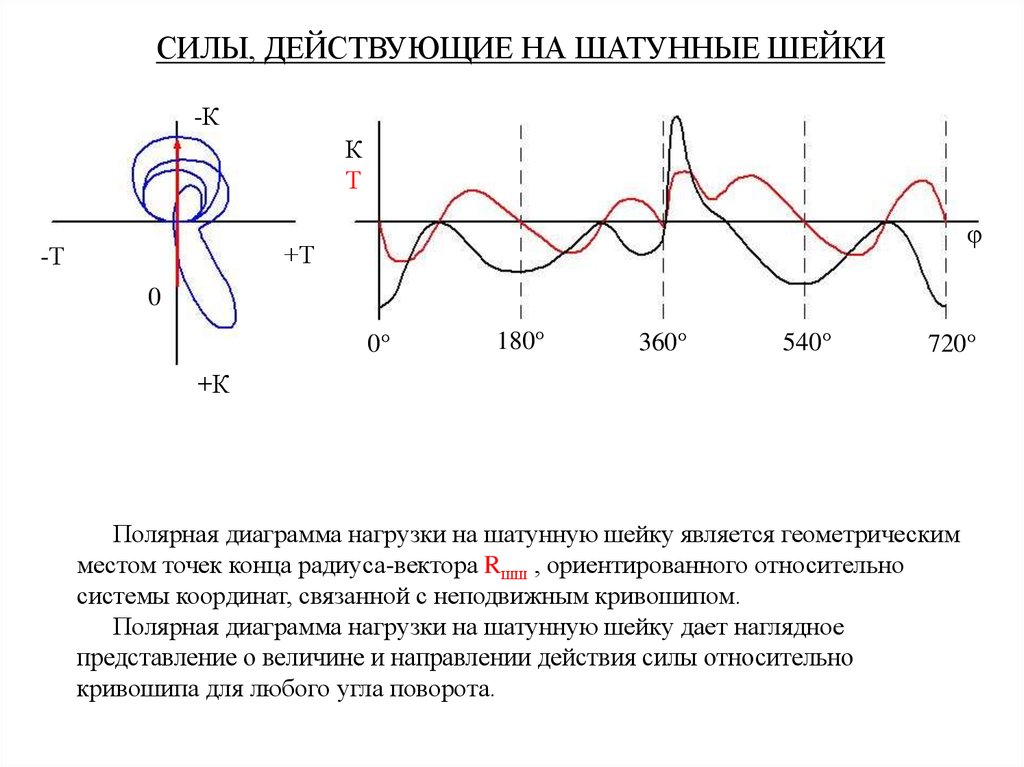
Полярная диаграмма нагрузки на шатунную шейку является геометрическим
местом точек конца радиуса-вектора Rшш , ориентированного относительно
системы координат, связанной с неподвижным кривошипом.
Полярная диаграмма нагрузки на шатунную шейку дает наглядное
представление о величине и направлении действия силы относительно
кривошипа для любого угла поворота.

12.

СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ
-К
К
Т
φ
+Т
-Т
0
0°
180°
360°
540°
720°
+К
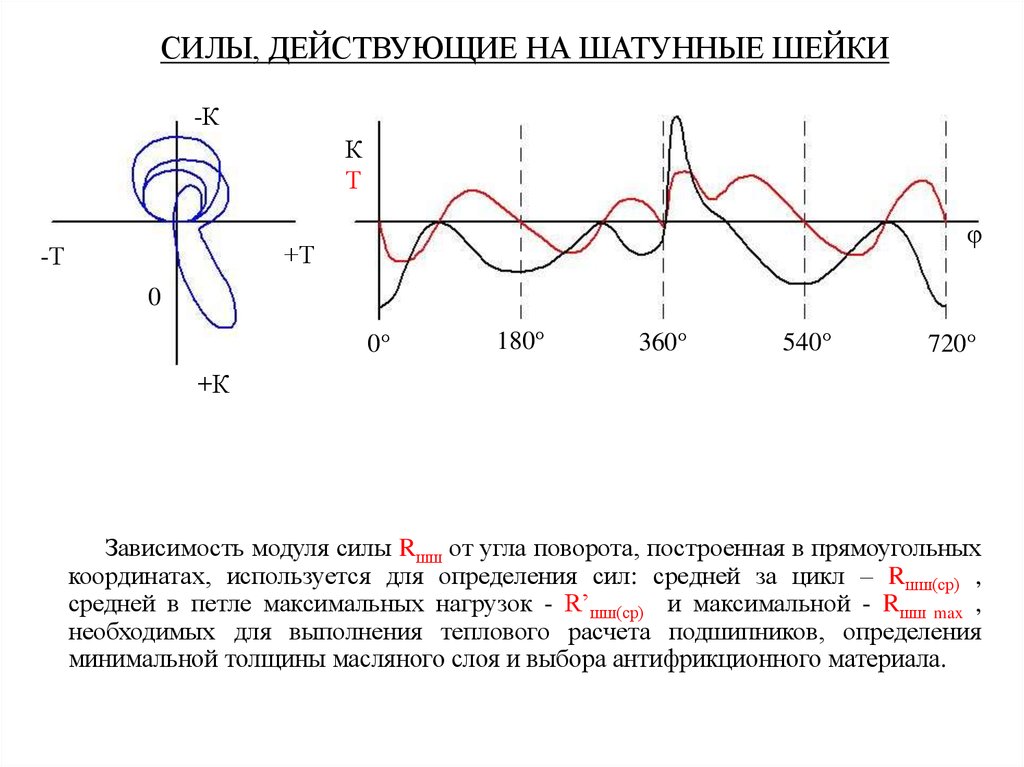
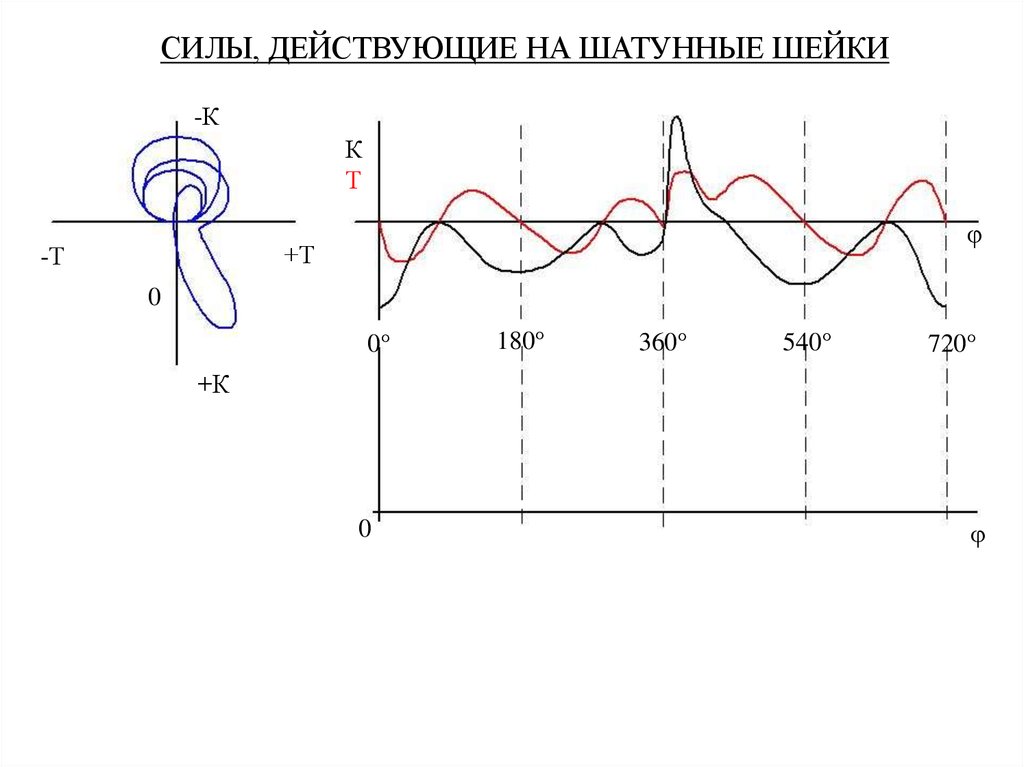
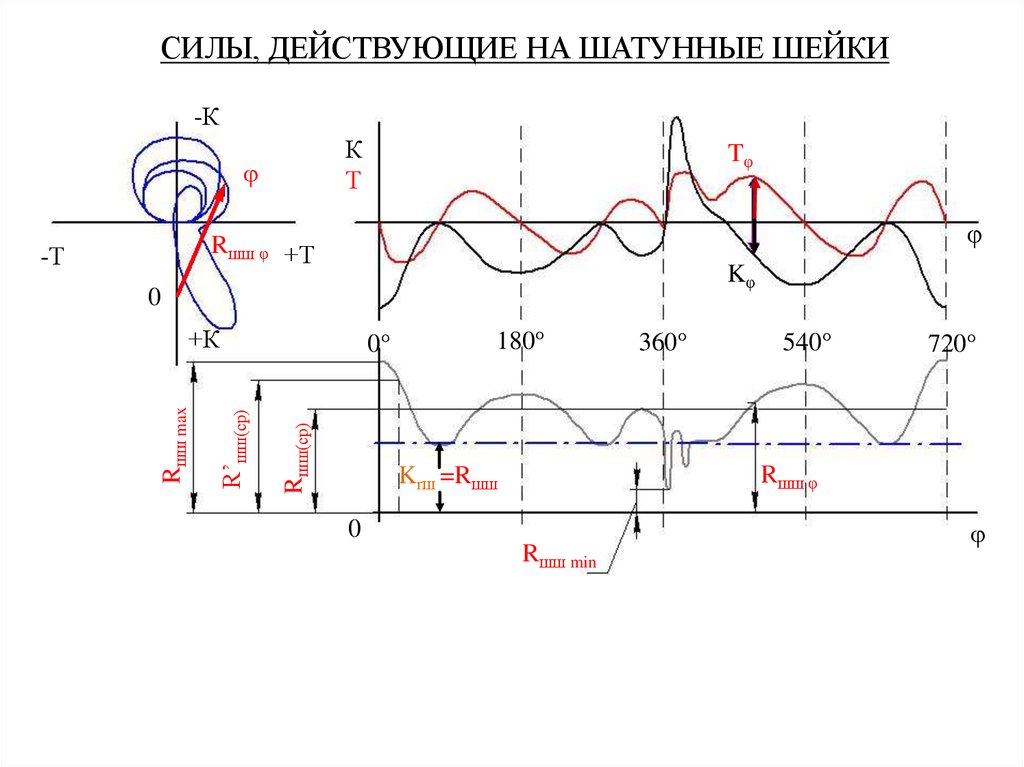
Зависимость модуля силы Rшш от угла поворота, построенная в прямоугольных
координатах, используется для определения сил: средней за цикл – Rшш(ср) ,
средней в петле максимальных нагрузок - R’шш(ср) и максимальной - Rшш max ,
необходимых для выполнения теплового расчета подшипников, определения
минимальной толщины масляного слоя и выбора антифрикционного материала.

13.

СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ
-К
К
Т
φ
+Т
-Т
0
0°
180°
360°
540°
720°
+К
0
φ

14.

СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ
-К
К
Т
φ
+Т
-Т
0
0°
180°
360°
540°
720°
+К
0
φ

15.

СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШАТУННЫЕ ШЕЙКИ
-К
К
Т
φ
Tφ
φ
Rшш φ +Т
-Т
Kφ
0
0°
Rшш(ср)
R’шш(ср)
Rшш max
+К
180°
360°
540°
720°
Rшш φ
Krш =Rшш
0
Rшш min
φ

16.

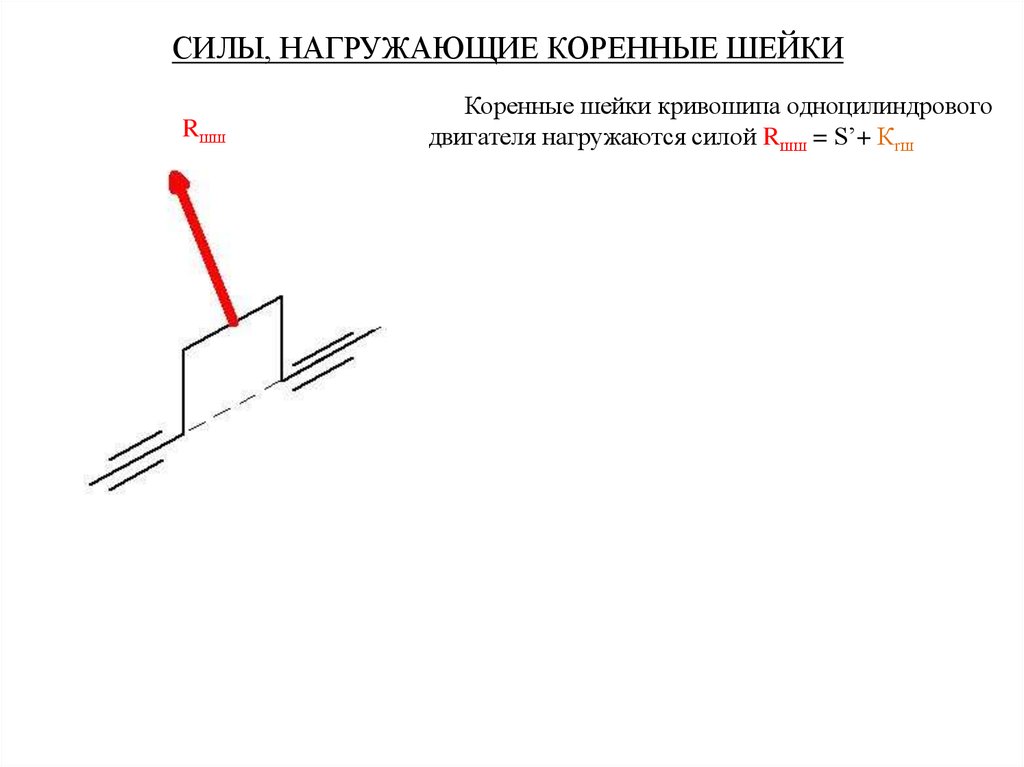
СИЛЫ, НАГРУЖАЮЩИЕ КОРЕННЫЕ ШЕЙКИ
Rшш
Коренные шейки кривошипа одноцилиндрового
двигателя нагружаются силой Rшш = S’+ Кrш

17.

СИЛЫ, НАГРУЖАЮЩИЕ КОРЕННЫЕ ШЕЙКИ
Rшш
Krk
Коренные шейки кривошипа одноцилиндрового
двигателя нагружаются силой Rшш = S’+ Кrш и
центробежной силой инерции неуравновешенных
масс кривошипа Кrк .

18.

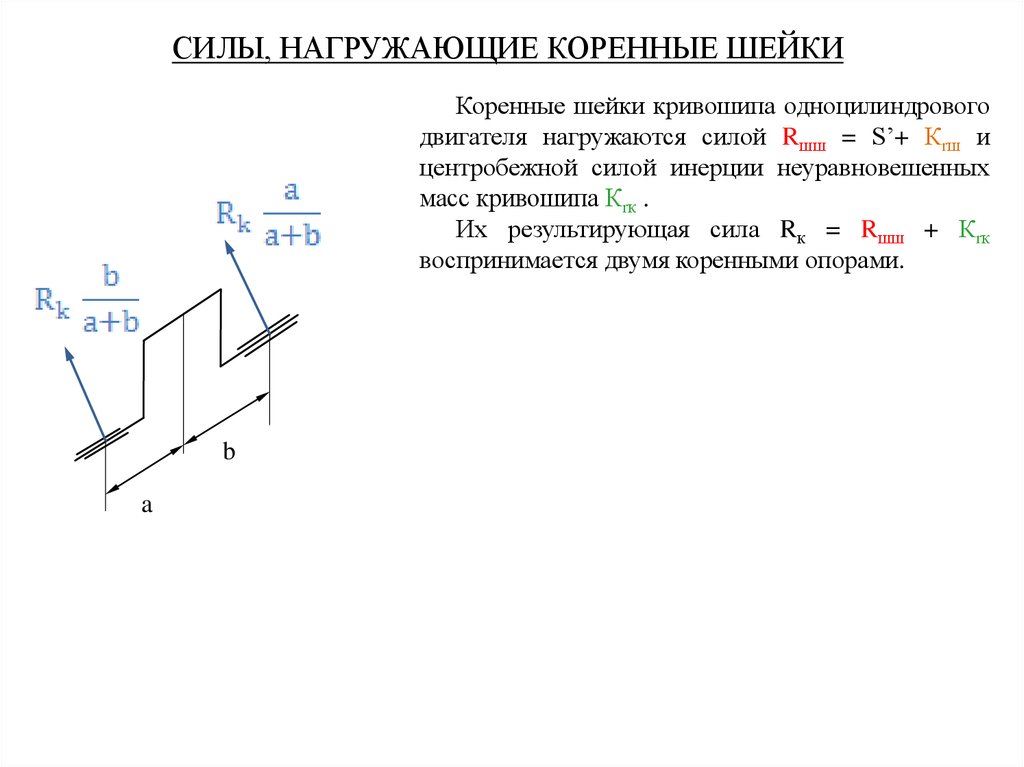
СИЛЫ, НАГРУЖАЮЩИЕ КОРЕННЫЕ ШЕЙКИ
Коренные шейки кривошипа одноцилиндрового
двигателя нагружаются силой Rшш = S’+ Кrш и
центробежной силой инерции неуравновешенных
масс кривошипа Кrк .
Их результирующая сила Rк = Rшш + Кrк
воспринимается двумя коренными опорами.
b
a

19.

СИЛЫ, НАГРУЖАЮЩИЕ КОРЕННЫЕ ШЕЙКИ
Коренные шейки кривошипа одноцилиндрового
двигателя нагружаются силой Rшш = S’+ Кrш и
центробежной силой инерции неуравновешенных
масс кривошипа Кrк .
Их результирующая сила Rк = Rшш + Кrк
воспринимается двумя коренными опорами.
b
a
Допущение: a=b

20.

СИЛЫ, НАГРУЖАЮЩИЕ КОРЕННЫЕ ШЕЙКИ
Коренные шейки кривошипа одноцилиндрового
двигателя нагружаются силой Rшш = S’+ Кrш и
центробежной силой инерции неуравновешенных
масс кривошипа Кrк .
Их результирующая сила Rк = Rшш + Кrк
воспринимается двумя коренными опорами.
Сила действующая на каждую коренную шейку
определяется выражением:
Допущение: a=b

21.

СИЛЫ, НАГРУЖАЮЩИЕ КОРЕННЫЕ ШЕЙКИ
Коренные шейки кривошипа одноцилиндрового
двигателя нагружаются силой Rшш = S’+ Кrш и
центробежной силой инерции неуравновешенных
масс кривошипа Кrк .
Их результирующая сила Rк = Rшш + Кrк
воспринимается двумя коренными опорами.
Сила действующая на каждую коренную шейку
определяется выражением:
Практически нагрузку на коренную шейку для
любого угла поворота кривошипа можно
определить, используя полярную диаграмму на
шатунную шейку.
Допущение: a=b

22.

Если полюс полярной диаграммы
перенести
в
точку
Ок
,
соответствующую началу вектора Кrк ,
направленного по оси кривошипа и
приложенного в точке Ош , получим
полярную диаграмму нагрузок на
коренные шейки.
0ш

23.

0ш
Если полюс полярной диаграммы
перенести
в
точку
Ок
,
соответствующую началу вектора Кrк ,
направленного по оси кривошипа и
приложенного в точке Ош , получим
полярную диаграмму нагрузок на
коренные шейки.
Уменьшение масштаба сил в два
раза даст действительные значения
нагрузок на коренную шейку.

24.

0ш
0к
Если полюс полярной диаграммы
перенести
в
точку
Ок
,
соответствующую началу вектора Кrк ,
направленного по оси кривошипа и
приложенного в точке Ош , получим
полярную диаграмму нагрузок на
коренные шейки.
Уменьшение масштаба сил в два
раза даст действительные значения
нагрузок на коренную шейку.

25.

0ш
0’к
0к
Kпр
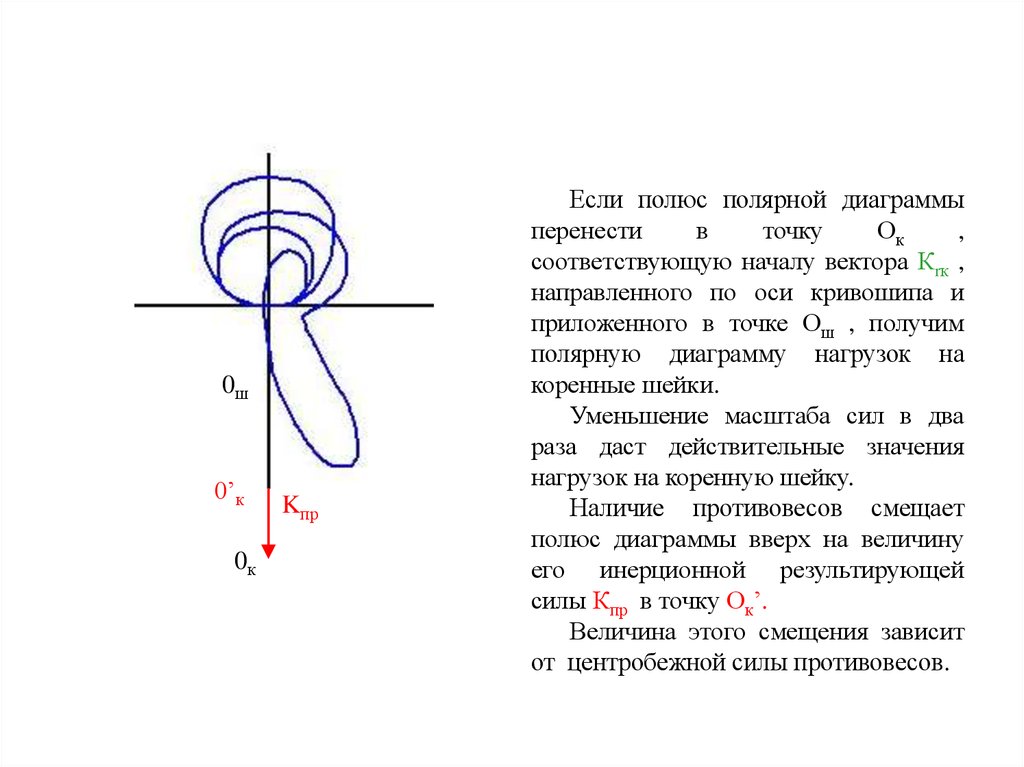
Если полюс полярной диаграммы
перенести
в
точку
Ок
,
соответствующую началу вектора Кrк ,
направленного по оси кривошипа и
приложенного в точке Ош , получим
полярную диаграмму нагрузок на
коренные шейки.
Уменьшение масштаба сил в два
раза даст действительные значения
нагрузок на коренную шейку.
Наличие противовесов смещает
полюс диаграммы вверх на величину
его инерционной результирующей
силы Кпр в точку Ок’.
Величина этого смещения зависит
от центробежной силы противовесов.

26.

0ш
0’к
0к
Если полюс полярной диаграммы
перенести
в
точку
Ок
,
соответствующую началу вектора Кrк ,
направленного по оси кривошипа и
приложенного в точке Ош , получим
полярную диаграмму нагрузок на
коренные шейки.
Уменьшение масштаба сил в два
раза даст действительные значения
нагрузок на коренную шейку.
Наличие противовесов смещает
полюс диаграммы вверх на величину
его инерционной результирующей
силы Кпр в точку Ок’.
Величина этого смещения зависит
от центробежной силы противовесов.

27.

Теоретическая диаграмма
износа шеек вала
Полярная диаграмма позволяет
построить
теоретическую
диаграмму износа шейки вала и
определить в первом приближении
положение
маслоподводящего
отверстия.
0

28.

Теоретическая диаграмма
износа шеек вала
Полярная диаграмма позволяет
построить
теоретическую
диаграмму износа шейки вала и
определить в первом приближении
положение
маслоподводящего
отверстия.
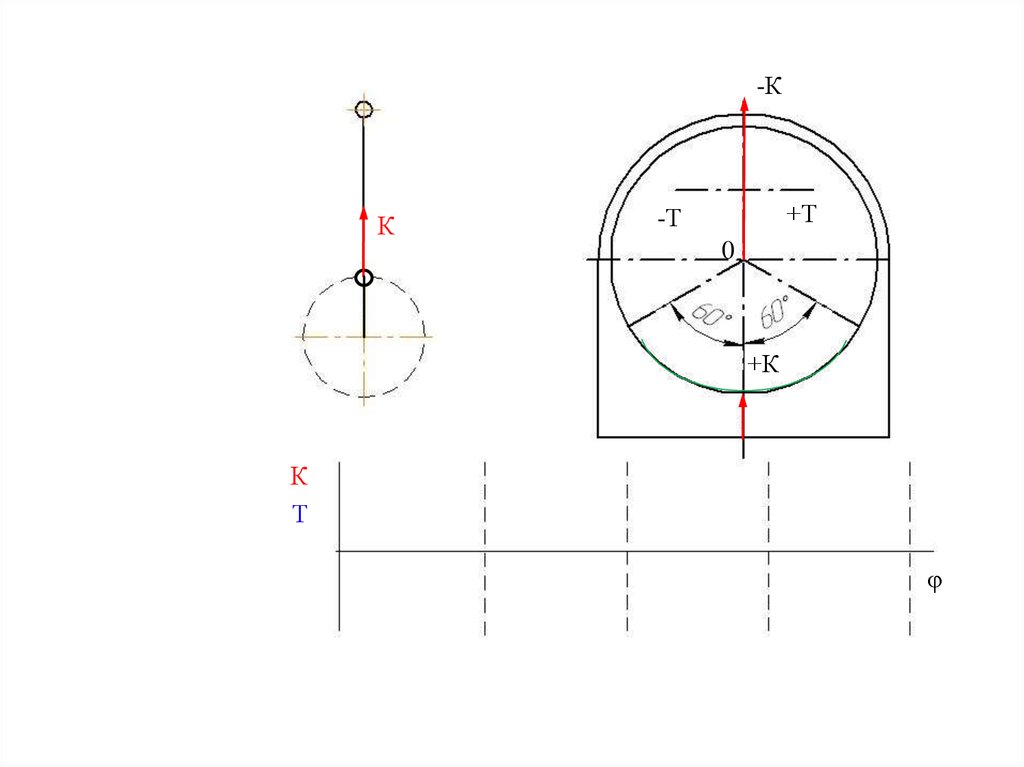
Необходимые допущения.
1. Величина
износа
шейки
пропорциональна силе и времени
действия.
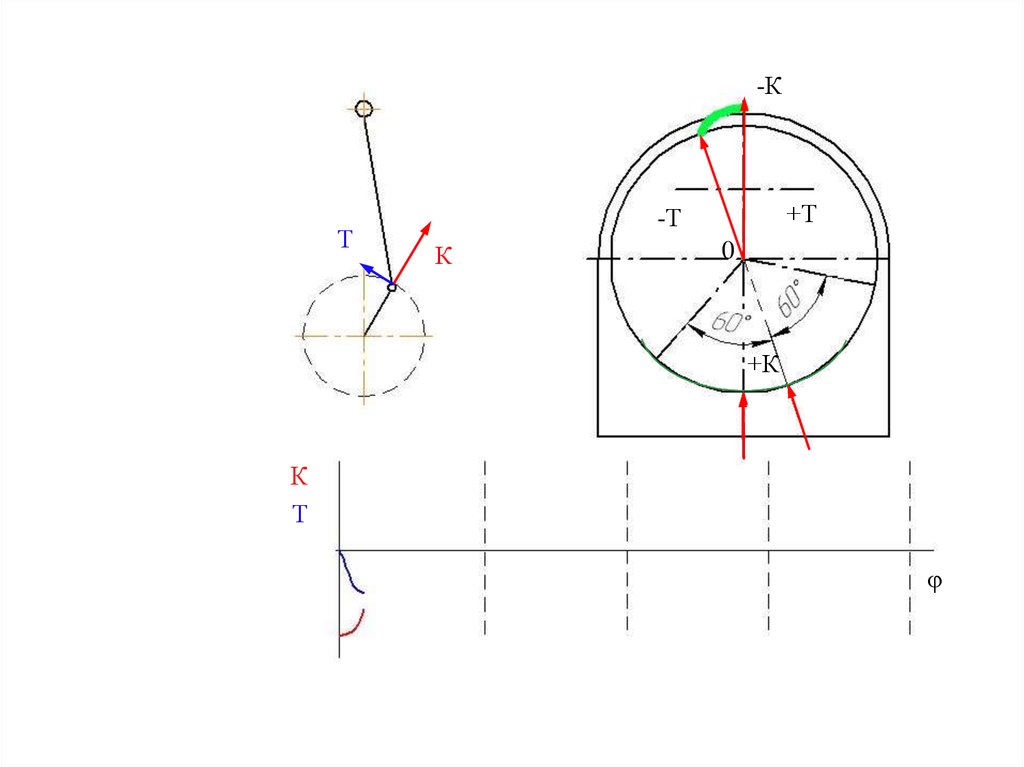
2. Износ равномерно распределен
в обе стороны от условной точки
положения силы на дугах в 60°,
что соответствует зоне контакта
вала и подшипника на дуге в 120°.
3. Коррозионный износ шеек при
этом отсутствует.

29.

-К
+Т
-Т
0
Кrш
+К
К
Т
φ

30.

-К
К
+Т
-Т
0
+К
К
Т
φ

31.

-К
Т
+Т
-Т
К
0
+К
К
Т
φ

32.

-К
+Т
-Т
0
+К
К
Т
К
Т
φ

33.

-К
К
+Т
-Т
0
+К
К
Т
φ

34.

-К
+Т
-Т
0
+К
К
К
Т
φ

35.

-К
К
+Т
-Т
0
+К
К
Т
φ

36.

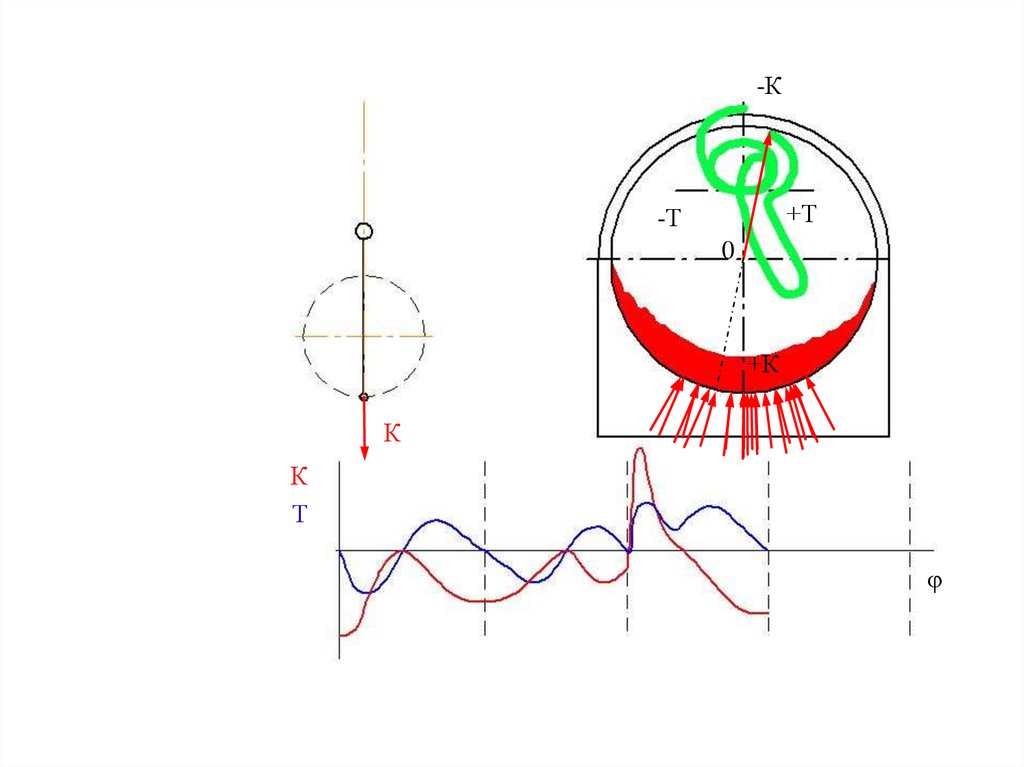
На
основании
полученной
теоретической
диаграммы
износа
шейки
вала
выбирается
ось
маслоподводящего отверстия, таким
образом, чтобы она проходила в зоне с
минимальным износом. Это связано с
тем, что в этой зоне наибольшая
величина зазора.

37.

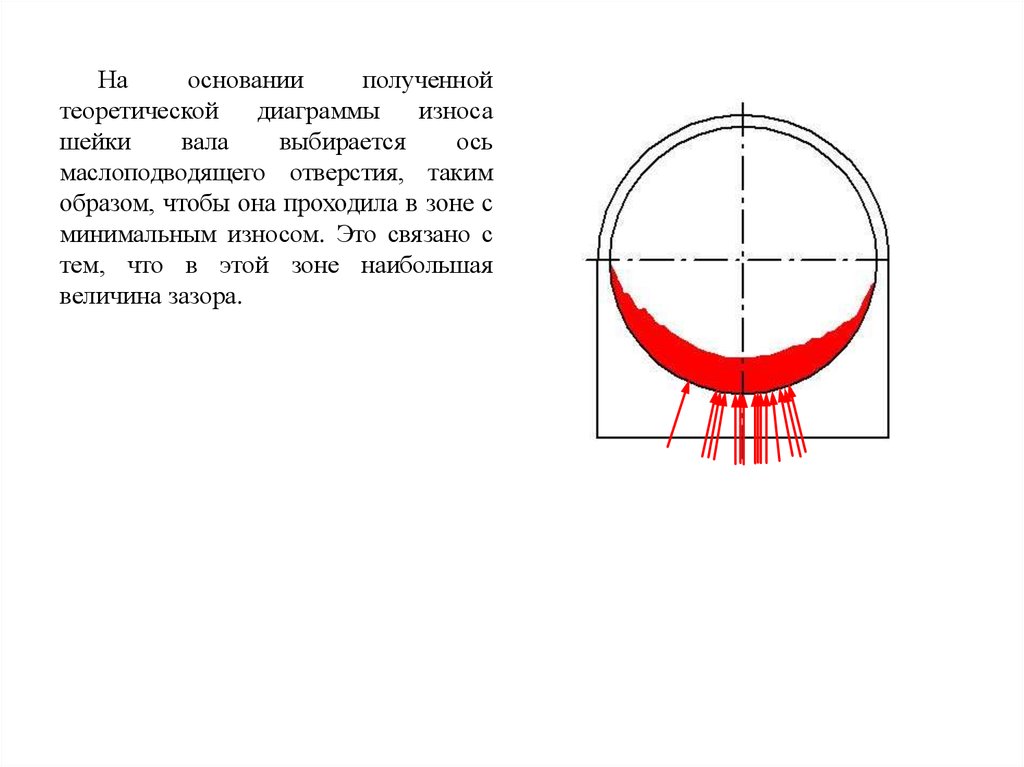
На
основании
полученной
теоретической
диаграммы
износа
шейки
вала
выбирается
ось
маслоподводящего отверстия, таким
образом, чтобы она проходила в зоне с
минимальным износом. Это связано с
тем, что в этой зоне наибольшая
величина зазора.
Ось маслоподводящего
отверстия