Похожие презентации:
Thiết kế các bộ lọc số
1. CHƯƠNG 7 Thiết kế các bộ lọc số
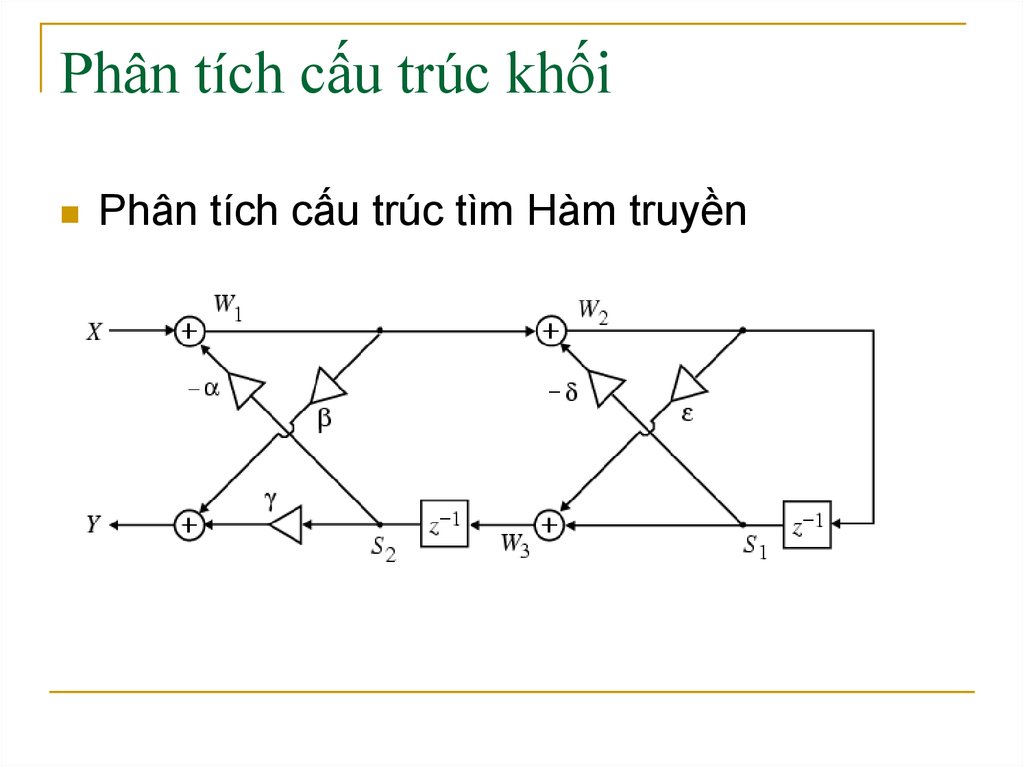
2. Phân tích cấu trúc khối
Phân tích cấu trúc tìm Hàm truyền3. Phân tích cấu trúc khối (tiếp)
Các tín hiệu ra tại các điểm trung gian làW1 X S2
W2 W1 S1
W3 S1 W2
Y W1 S2
Từ hình vẽ chúng ta có
S2 z 1W3
S1 z 1W2
4. Phân tích cấu trúc khối (tiếp)
Thay thế 2 biểu thức dưới vào 4 biểu thứctrên ta có
W1 X z 1W3
W2 W1 z 1W2
W3 z 1W2 W2
Y W1 z 1W3
Từ biểu thức thứ 2 ta có W2 W1 /(1 z 1 )
Và từ biểu thức thứ 3
W3 ( z 1)W2
5. Phân tích cấu trúc khối (tiếp)
Kết hợp 2 biểu thứcz 1
W3
W1
1
1 z
Thay thế biểu thức trên vào
W1 X z 1W3 , Y W1 z 1W3
Thu được
Y ( ) z 1 z 2
H ( z)
X 1 ( ) z 1 z 2
6. Thiết kế bộ lọc FIR
Một bộ lọc đáp ứng xung hữu hạn với hàmhệ thống có dạng:
Như vậy đáp ứng xung h(n) là
7. Thiết kế bộ lọc FIR (tiếp)
Phương trình sai phân làBậc của bộ lọc là M-1, trong khi chiều dài của
bộ lọc là M
Thi hành bằng Matlab
Hàm: y = filter(b,1,x)
8. Hàm fir1
Bộ lọc FIR bằng phương pháp cửa sổb = fir1(n,Wn)
b = fir1(n,Wn,'ftype')
b = fir1(n,Wn,window)
b = fir1(n,Wn,'ftype',window)
b = fir1(...,'normalization')
9. b = fir1(n,Wn)
Lọc thông thấp, b = fir1 (n,Wn,'low')n: bậc của bộ lọc
Wn: tần số cắt có giá trị 0<Wn<1.0 với 1.0
tương ứng với ½ tần số lấy mẫu
b có giá trị thực và pha tuyến tính, lọc tại tần
số Wn đạt -6 dB
b = fir1(N,Wn,'high')
10. b = fir1(n,Wn) với Wn = [W1 W2]
thiết kế bộ lọc giải thôngWn = [W1 W2], W1 < W < W2
tương tự như b = fir1(n,Wn,'bandpass')
Lọc giải chắn: b = fir1(n,Wn,'stop')
11. b = fir1(n,Wn,WIN)
Thiết kế bộ lọc với các hàm cửa sổb = fir1(n,Wn,kaiser(N+1,4)) dùng cửa sổ
Kaiser với beta=4.
b = fir1(n,Wn,'high',chebwin(N+1,R))
12. Thiết kế bộ lọc IIR
Tổng hợp bộ lọc số IIR trên cơ sở bộ lọctương tự,
Tổng hợp bộ lọc tương tự
Dùng các phương pháp chuyển đổi tương
đương một cách gần đúng từ bộ lọc tương tự
sang bộ số.
13. Bộ lọc số đáp ứng xung vô hạn (IIR)
y(n) p0 x(n) p1x(n 1) ... pM1 x(n M1 )d1 y(n 1) d 2 y(n 2) ... d M 2 y(n M 2 )
M1
Y ( z)
H ( z)
X ( z)
p
m
z
m 0
M2
d
m 0
m
z
m
m
14. Bộ lọc số đáp ứng xung vô hạn
Các kỹ thuật cơ bản được gọi là các phépbiến đổi lọc A/D.
Các bảng AFD chỉ dùng cho các bộ lọc thông
thấp. Trong khi ta cần thiết kế các bộ lọc
chọn tần khác (thông cao, thông dải, chắn
dải, v.v…)
Cần áp dụng các phép biến đổi băng tần đối
với các bộ lọc thông thấp. Các phép biến đổi
này cũng được gọi là ánh xạ giá trị-phức, và
chúng cũng có sẵn trong thư viện.
15. Cách tiếp cận Matlab
Thiết kế bộ lọc tuần tựChuyển đổi hệ số bộ lọc
từ analog sang bộ lọc kỹ thuật số
s z
16. Thiết kế bộ lọc tương tự
Các kỹ thuật thiết kế lọc IIR dựa trên bộ lọcanalog đã có để thu được các bộ lọc số.
Chúng ta thiết kế các bộ lọc analog nay theo
các bộ lọc điển hình.
Ba kiểu được sử dụng rộng rãi trong thực tế
Thông thấp Butterworth
Thông thấp Chebyshev (Kiểu I và II)
Thông thấp Elliptic
17. Hàm afd_chb1
Để thiết kế một bộ lọc analog chuẩn hoá:Chebyshev-1
[b,a] = afd_chb1(Wp,Ws,Rp,As)
b = các hệ số đa thức tử số của Ha(s)
a = các hệ số đa thức mẫu số cảa Ha(s)
Wp: tần số cắt dải thông theo đơn vị rad/sec; Wp >0
Ws: tần số cắt dải chắn theo đơn vị rad/sec;
Ws>Wp >0
Rp: độ gợn dải thông theo đơn vị dB; (Rp > 0)
As: độ suy giảm dải chắn theo đơn vị +dB; (Ap > 0)
18. Chuyển đổi hệ số bộ lọc từ analog sang bộ lọc kỹ thuật số sz
Chuyển đổi hệ số bộ lọc từ analog sangbộ lọc kỹ thuật số s z
Biến đổi song tuyến tính
Ánh xạ này là phương pháp biến đổi tốt nhất.
Linear fractional transformation
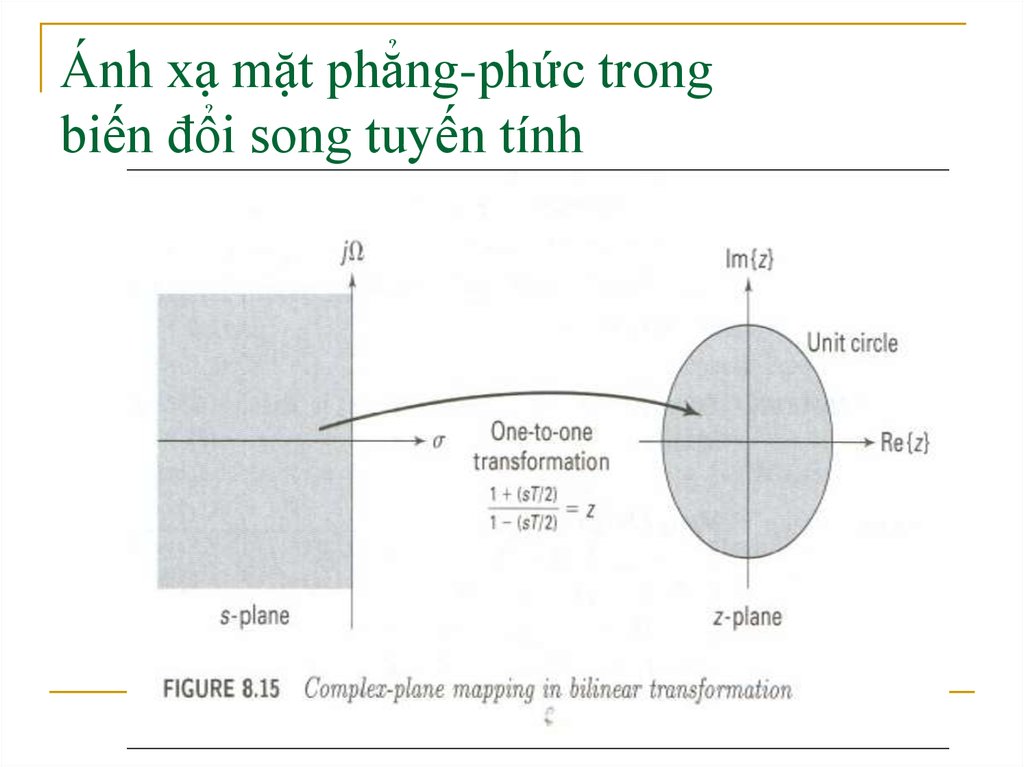
19. Ánh xạ mặt phẳng-phức trong biến đổi song tuyến tính
20. Các nhận xét
Sigma < 0 |z| < 1, Sigma = 0 |z| = 1, Sigma > 0|z| > 1
Toàn bộ mặt phẳng-nửa trái ánh xạ vào bên trong
vòng tròn đơn vị. Đây là phép biến đổi ổn định.
Trục ảo ánh xạ lên đường tròn đơn vị là ánh xạ 1-1.
Do đó không có aliasing trong miền tần số.
Quanhệ của ω theo Ω là phi tuyến
ω= 2tan-1(ΩT/2)↔ Ω=2tan(ω/2)/T;
Function [b,a] = bilinear(c,d,Fs)
21. Hàm bilinear
Hàm bilinear dùng để chuyển đổi các hệ sốbộ lọc từ analog sang bộ lọc kỹ thuật số
[b,a] = bilinear (Z,P,K,Fs)
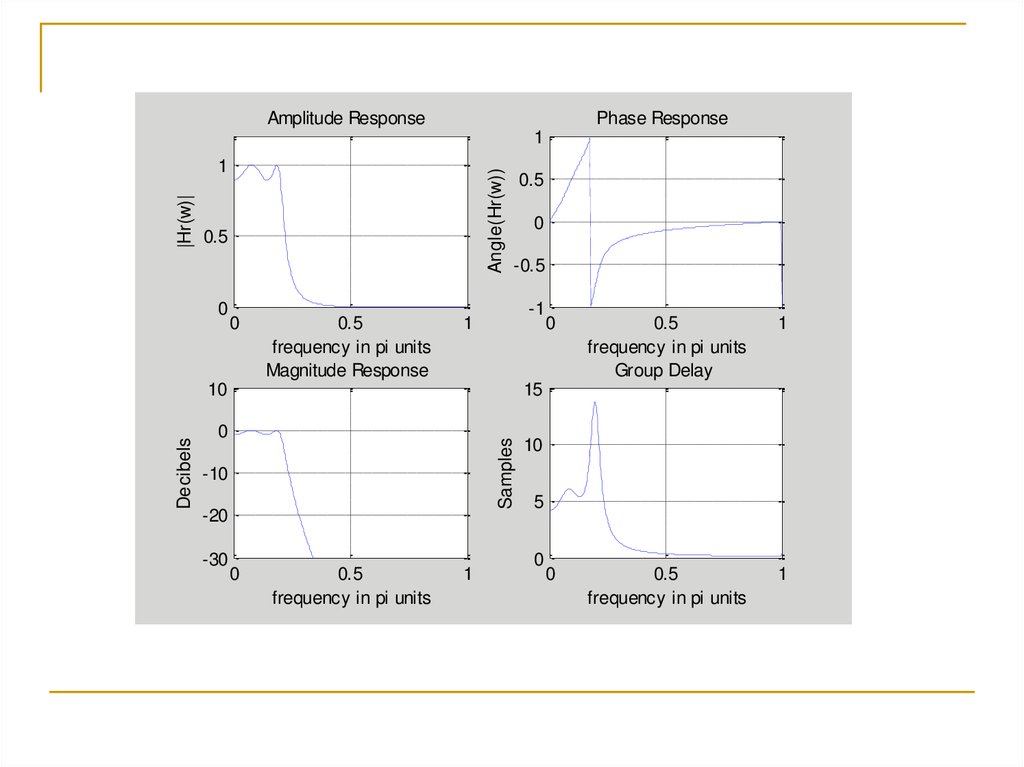
22. Ví dụ chương trình Matlab
% Chi tieu ky thuat cua bo loc so:wp =0.2*pi; % digital Passband freq in Hz
ws =0.3*pi; % digital Stopband freq in Hz
Rp = 1; % Passband ripple in dB
As = 15; % Stopband attenuation in dB
% Chi tieu ky thuat cua bo loc tuong tu: Anh xa nguoc
T = 1; Fs =1/T; % Dat T=1
OmegaP = (2/T)*tan(wp/2);
OmegaS = (2/T)*tan(ws/2);
% Tinh toan bo loc tuong tu:
[cs, ds] = afd_chb1(OmegaP,OmegaS,Rp,As);
% Bien doi song tuyen:
[b,a] = bilinear(cs,ds,Fs);
23.
Amplitude ResponsePhase Response
1
Angle(Hr(w))
|Hr(w)|
1
0.5
0
0
0.5
frequency in pi units
Magnitude Response
0.5
0
-0.5
-1
1
0
-10
-20
-30
0.5
frequency in pi units
Group Delay
1
0
0.5
frequency in pi units
1
15
Samples
Decibels
10
0
0
0.5
frequency in pi units
1
10
5
0








![b = fir1(n,Wn) với Wn = [W1 W2] b = fir1(n,Wn) với Wn = [W1 W2]](https://cf2.ppt-online.org/files2/slide/v/vMrPetw0n7igCD1ZIc5JL6pAUGWdfVjEKFk3aHozm/slide-9.jpg)












 Программирование
Программирование
