Похожие презентации:
Частицы и взаимодействия. Ускорители частиц. Элементарные частицы. Экспериментальное исследование структуры частиц. (Лекция 9)
1.
2.
Лекция 91.Частицы и взаимодействия.
2. Ускорители частиц.
3. Элементарные частицы.
4. Экспериментальное исследование
структуры частиц.
5. Типы, радиусы и константы взаимодействий частиц.
6. Диаграммы Фейнмана для электромагнитных взаимодействий.
7. Кванты других полей.
2
3.
1.ВведениеЭлементарные частицы – это мир объектов
~ 1 Фм.
В настоящее время установлено существование
кварков и лептонов, размеры которых ~ 10-3 Фм. и
считается, что все сильно взаимодействующие
частицы состоят из кварков. Исследование малых
областей пространства требует концентрации
энергии, поскольку лишь при λ < RЯ возможно
проникновение во внутрь ядра:
h 2 c 1200МэВ Фм
p
pc
Е МэВ
3
4.
2. Ускорители.Изменение энергии частиц осуществляется в
ускорителях на встречных пучках (коллайдерах). Это позволяет исключить потери энергии
на движение центра масс, что происходит в
линейных ускорителях. Оба типа ускорителей
эквивалентны, если mа =mb =m и одинакова
энергия, вкладываемая в полезную часть
реакции.
4
5.
56.
Заадача 1. Получим формулу , связывающуюТа и Та‘ в эквивалентных ускорителях, исходя
из понятия минимального порога реакции:
'
а
'
b
'
; а T ; для а b M
(СЦИ ) Мс 2Т
Епор
2
2
m Mc
Епор ( ЛСК ) Мс 1
T
2
m 2mc
(СЦИ )
Епор ( ЛСК ) Епор
2
6
7.
m T2mc T
T 2T 1 2 2T (
)
2
mc
m mc
в ультрареля тивистском случае
2
2(T )
T
; при va va
2
mc
2
Задача 2. Далее, найдем максимальную
массу частицы (М), которую можно получить
на ускорителе на встречных пучках, если:
Та ≠ Тb. Запишем закон сохранения энергии и
7
импульса:
8.
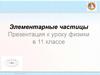
Т а Т b Мс Т M1
pM Ta Tb
c
pa pb pM
2
Мс Т M ( pM c) М с
2
2
2 4
(Т а Т b ) ( pM c) М с
2
2
2 4
(Ta Tb ) М с Mc 2 TaTb
2
2 4
2
8
9.
В ускорителях, заряженные частицыдвижутся по кольцу, проходя промежутки с
ускоряющим переменным полем. Частицы
увеличивают свою энергию и удерживаются
на орбите нарастающим магнитным полем.
По достижению Hmax , частицы направляются на неподвижную мишень или во встречный поток частиц.
9
10.
3. Элементарные частицы.Всего имется около 500 элементарных
,
частиц : p, n, e , , , ,W , , ....
0
Стабильные частицы : p, p, e , , , ,
распад этих частиц не наблюдался и
время их жизни равно : e 4.2 10 лет;
24
р 10 лет;
39
св
n
900c; вселен. 10 лет
10
10
11.
Элементарной частицей называетсяобъект размером 1 Фм, который не
распадаетс я на составные части,
например : продукты распада нейтрона
не являются его составными частями, а
рождаются в момент его распада
n p e e
11
12.
Время жизни частиц меняется впределах : 10
Ж 10
20
24
6
с Ж 10 с. Частицы с
с называются резонансам и.
Их можно рассматривать как возбужденные
состояния стабильных или квазистабильных
частиц. Резонансы распадаются за счет
сильных взаимодействий и время
Трасп = 10 -22 -10 -24 с.
12
13.
Квазистабильные частицы распадаютсямедленно,.Трасп>10 -20c , вследствие электромагнитных или слабых взаимодействий. Большинство (~450) известных
частиц (адроны) состоят из двух кварков
(мезоны) или трех кварков (барионы):
адроны↔ мезоны и барионы.
13
14.
На современном уровне знаний шестьлептонов : e, , , e , , и шесть
кварков : d , u , s, c, b, t являются
бесструкту рными с размерами 1Фм
14
15.
4. Экспериментальное исследованиеструктуры частиц.
Для изучения формы, размеров, распределения электрического заряда и магнитного
момента частиц используют метод упругого
рассеяния электронов. Сечение упругого
рассеяния электрона на протоне:
р
2
d d
Fp (q )
d p d МОТТА
15
16.
В 1951г. Ферми обнаружил возбужденноесостояние протона в реакции:
(ud ) p (uud ) (uuu ) p
p p ; T 200 МэВ; T 300 МэВ
*
1
p (uud ) p ( ) ; s p ; m p 938,27
2
3
*
(uuu ) p ( ) ; s p* ; m p* 1232
2
3
*
(uud ) p ( ) ; s p* ; m p* 1232
2
16
17.
+ p p*17
18.
Таким образом, в первом возбужденномсостоянии происходит переворот спина
кварка относительно исходного
состояния. Энергия этого переворота
около 300МэВ.
Из рисунка видно, что :
120 МэВ; тогда :
Ж
23
3 10 с
18
19.
5. Типы, радиусы и константывзаимодействий частиц.
В физике фундаментальных взаимодействий наиболее существенны сильные,
электромагнитные и слабые взаимодействия. При экстремально больших массах
(>1019 ГэВ) необходимо учитывать гравитационные силы. Для описания процессов
в мире частиц служит релятивистская квантовая теория или квантовая теория поля.19
20.
Нобелевские премии:В 1965 г. Фейман, Швингер, Томонага разработали вариант этой теории для описания электромагнитных взаимодействий – квантовую
электродинамику (КЭД). В 1979 г. Глэшоу,
Салам, Вайнберг создали теорию взаимодействия кварков и лептонов, объединяющую
электромагнитное и слабое взаимодействие –
электрослабая модель (ЭСМ), которая включает КЭД. Для описания сильных взаимодействий
разработана квантовая хромодинамика (КХД).
20
21.
1965 г. – Фейман, Швингер, Томонага – КЭД.1979г. Глэшоу, Салам, Вайнберг -ЭСМ ( КЭД)
ЭСМ и КХД совместно описывают сильное, слабое и
электромагнитное взаимодействие кварков и лептонов
и образуют схему, называемую
стандартной моделью.
21
22.
ЭСМ и КХД совместно описывают сильное,слабое и электромагнитное взаимодействие
кварков и лептонов и образуют схему, называемую стандартной моделью.
22
23.
Удобной иллюстрацией процессов в миречастиц являются диаграммы Фейнмана,
которые позволяют оценить вероятности этих
процессов взаимодействия. С помощью этих
диаграмм можно записать амплитуду
вероятности взаимодействия частиц (А) и,
просуммировав амплитуды для всех возможных
диаграмм процесса, получить эффективное
сечение d /dΩ.
23
24.
6. Диаграммы Фейнмана для Е-Hвзаимодействий.
Рис. 3 Рассеяние электронов
24
25.
На рис. 3 представлена типичная диаграмма восях (x,t). Внешним незамкнутым линиям
отвечают волновые функции реальных частиц
до и после взаимодействия.
Внутренним линиям отвечают виртуальные
частицы, распространяющиеся от точки
испускания до точки поглощения. Функция
распространения в этом случае называется
пропагатором.
В каждом узле выполняются все законы сохранения, присущие данному взаимодействию.
25
26.
Согласно квантовой теории поля взаимодействие между частицами осуществляетсяпутем обмена некоторой третьей частицей,
которая является квантом поля или переносчиком взаимодействия. Например, для
электрона взаимодействие осуществляется
путем обмена фотоном.
В т.А –узел, вершина диаграммы, испускается -квант и электрон испытывает отдачу.
При этом нарушается закон сохранения
полной энергии, поэтому испускаемый фотон
является виртуальным и существует в
26
течение времени
27.
t; расстояние ухода кванта
E
с
с t
увеличивае тся со временем ,
E
поэтому энергия взаимодействия
уменьшается, как в законе Кулона .
В т. B виртуальный -квант поглощается и
баланс по энергии восстанавливается.
27
28.
С помощью таких диаграмм можно рассчитать амплитуду вероятности, А~α½, выделенного процесса и, просуммировав эти амплитуды для всех возможных диаграмм,рассчитать эффективное сечение процесса А2.
Вероятность процесса взаимодействия зависит
от трех факторов:
1. Значения константы для процесса.
28
29.
2. Степенью нарушения соотношения прирождении виртуальной частицы:
2
2
2 4
E ( pc) m c ; чем сильнее нарушение
тем ниже вероятность процесса.
3. Полной энергией процесса; чем выше
энергия, тем выше вероятность.
Если узел диаграммы состоит из трех линий,
то амплитуда вероятности А процесса:
29
30.
A ~ ; если узлов N , то АN ~ ( ) ,N
например : е е рассеяние :
Аее ( ) ; а вероятность
2
d
2
2
I
Aee
d
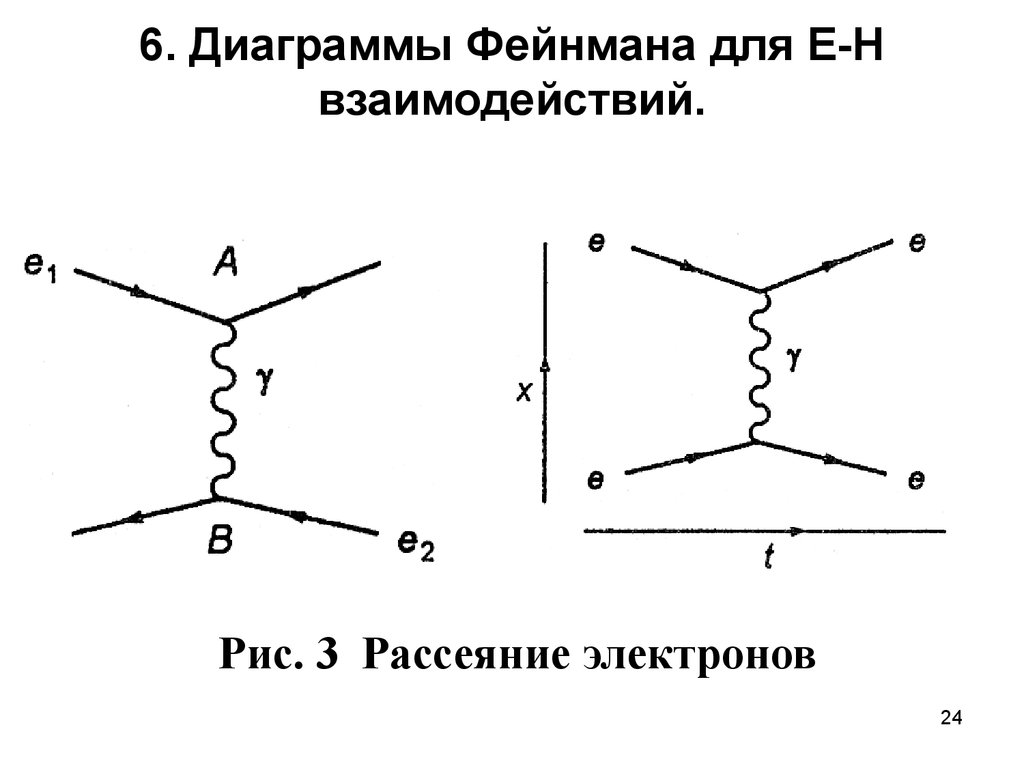
Пример: Рассеяние фотона на электроне эффект Комптона.
30
31.
Рис.8.4 Рассеяние фотона на электроне эффект Комптона.31
32.
Здесь возможны две двухузловые диаграммы. В обоих случаях виртуальной частицейявляется электрон, однако в первом случае
происходит поглощение фотона, а во втором
–сначала испускание и затем поглощение.
Поэтому амплитуда вероятности Комптонэффекта есть сумма амплитуд соответствующих диаграмм:
32
33.
2d
А1 А2
d комп
~ ~ e ; где е е
е е
2
22
2
1
с
137
Если вместо электрона будет объект с
2
e
4
зарядом Ze, то А ~ Z e e Z e
d
2 2
2 4
~ Z e ~ Z e , как и в формуле
d
Резерфорда
33
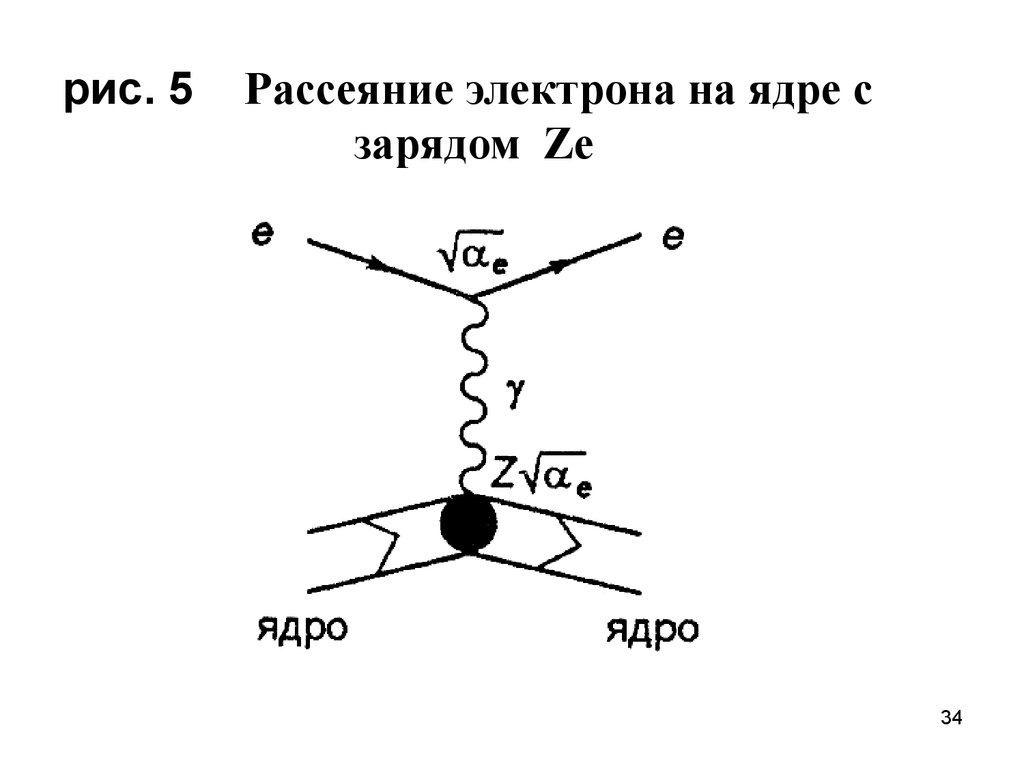
34.
рис. 5Рассеяние электрона на ядре с
зарядом Ze
34
35.
Увеличение числа узлов на диаграмме надва, уменьшает вероятность процесса в 10 4
раз. Следовательно, в электромагнитных
процессах можно обойтись двухузловыми
диаграммами.
Пример: Диаграммы для е-е рассеяния.
35
36.
Рис.8.6Диаграммы для е-е рассеяния.
36
37.
Для слабых взаимодействий подход аналогичен. В сильных взаимодействиях необходимоучитывать множество диаграмм, что осложняет
расчеты.
В заключение отметим, что каждому взаимодействию присущ свой заряд: сильный, электрический, слабый, гравитационный, соответственно:
S ; e ; ;
G
37
38.
7. Кванты других полей.38







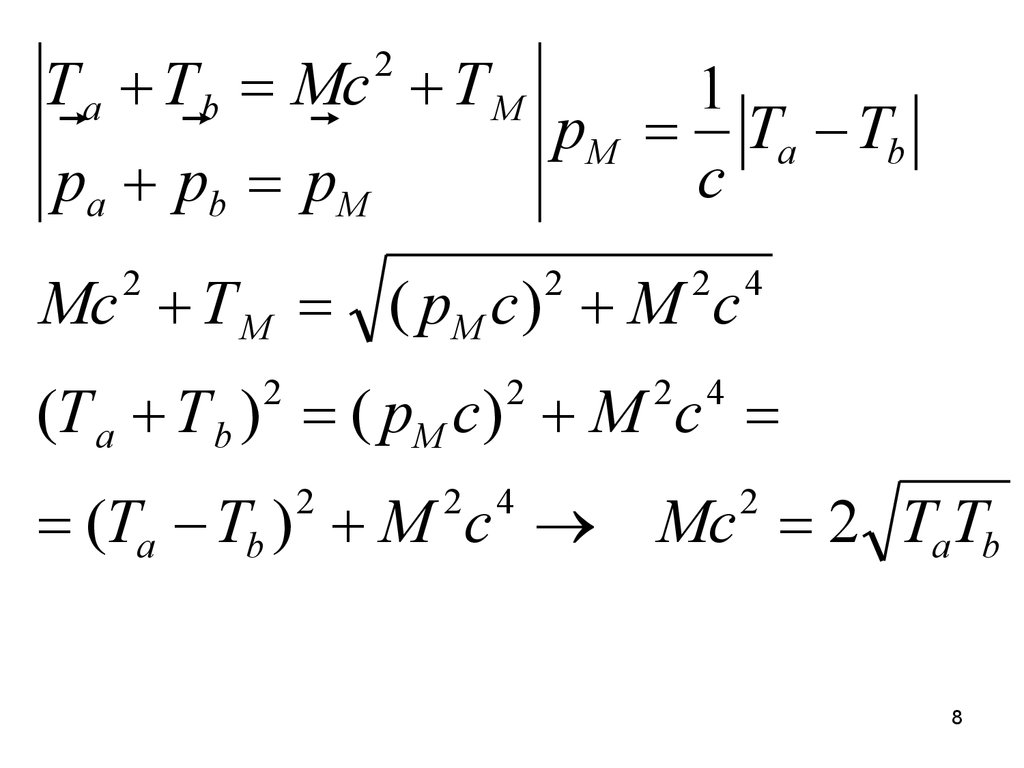




























 Физика
Физика