Представление чисел. 10 класс

1. Представление чисел

29.09.2019
Представление чисел
10 класс

2. Машинное слово

Элементарная ячейка памяти ЭВМ имеет длину
8 бит (байт)
Каждый байт имеет свой номер (его называют адресом)
Наибольшую последовательность бит, которую ЭВМ
может обрабатывать как единое целое, называют
машинным словом
Длина машинного слова зависит от разрядности
процессора и может быть равной 16, 32, 64 битам и т.д.

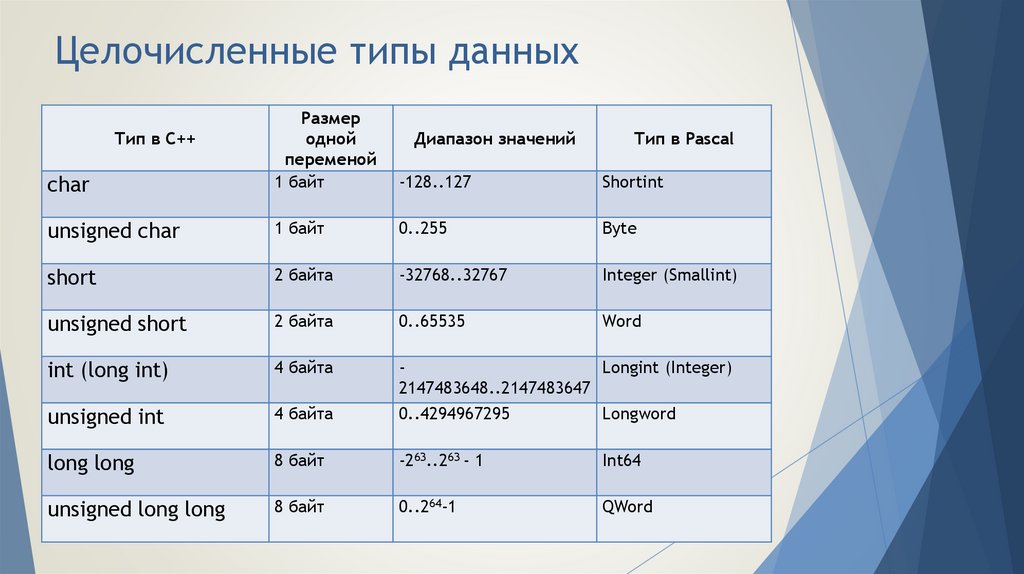
3. Целочисленные типы данных

char
Размер
одной
переменой
1 байт
-128..127
Shortint
unsigned char
1 байт
0..255
Byte
short
2 байта
-32768..32767
Integer (Smallint)
unsigned short
2 байта
0..65535
Word
int (long int)
4 байта
Longint (Integer)
2147483648..2147483647
unsigned int
4 байта
0..4294967295
Longword
long long
8 байт
-263..263 - 1
Int64
unsigned long long
8 байт
0..264-1
QWord
Тип в C++
Диапазон значений
Тип в Pascal

4. Прямой код

Прямой код — способ представления двоичных чисел с
фиксированной запятой в компьютерной арифметике
Главным образом используется для записи
неотрицательных чисел
В случае использования прямого кода для чисел как
положительных, так и отрицательных, то есть чисел,
запись которых подразумевает возможность
использования знака минус (знаковых чисел),
хранимые цифровые разряды числа дополняются
знаковым разрядом

5. Прямой код

При записи числа в прямом коде старший разряд
(старший бит) объявляется знаковым разрядом
(знаковым битом)
Если знаковый бит равен 0, число положительное,
иначе — отрицательное
В остальных разрядах (которые называются цифровыми
разрядами) записывается двоичное представление
модуля числа

6. Прямой код

Его легко получить из представления целого числа в
любой другой системе счисления
Для этого достаточно перевести число в двоичную
систему счисления, а затем заполнить нулями
свободные слева разряды разрядной сетки машины

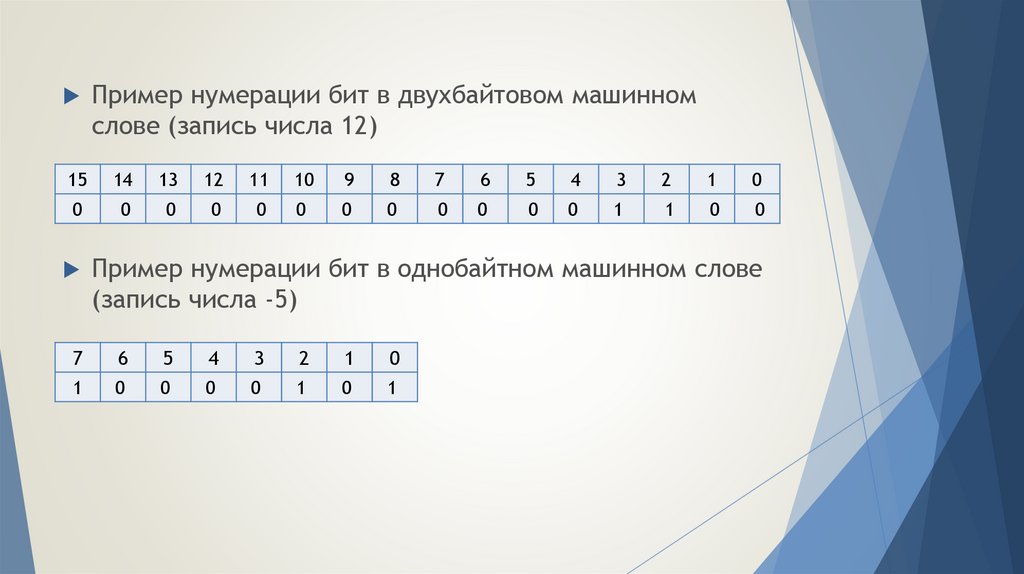
7.

Пример нумерации бит в двухбайтовом машинном
слове (запись числа 12)
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
Пример нумерации бит в однобайтном машинном слове
(запись числа -5)
7
6
5
4
3
2
1
0
1
0
0
0
0
1
0
1

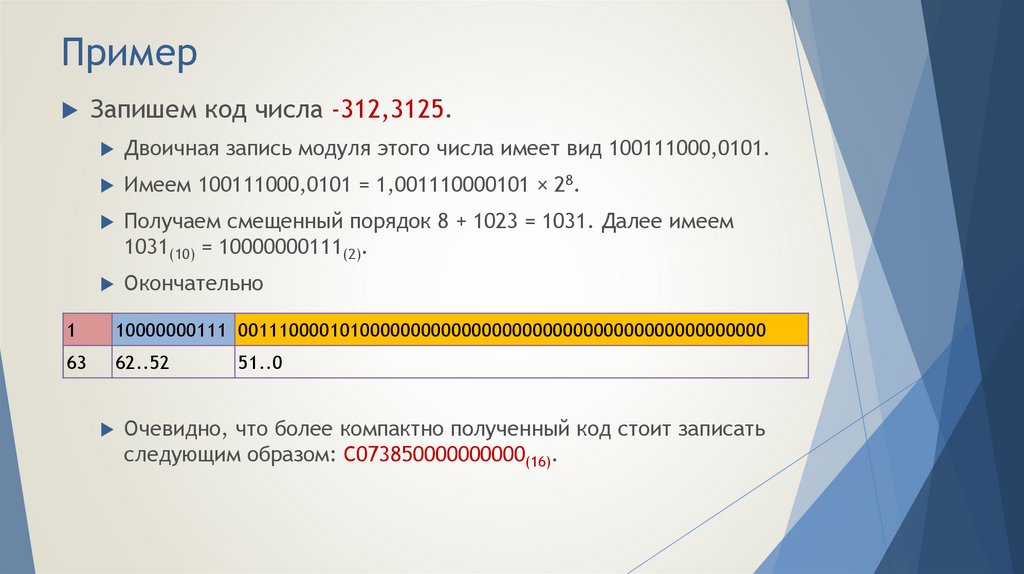
8. Пример

Если число 37(10) = 100101(2) объявлено величиной типа
short (шестнадцатибитовое со знаком), то его прямым
кодом будет
0000000000100101
Если величиной типа int (тридцатидвухбитовое со
знаком), то его прямой код будет
00000000000000000000000000100101
Для более компактной записи чаще используют
шестнадцатеричное представление кода
Полученные коды можно переписать соответственно как
0025(16) и 00000025(16)

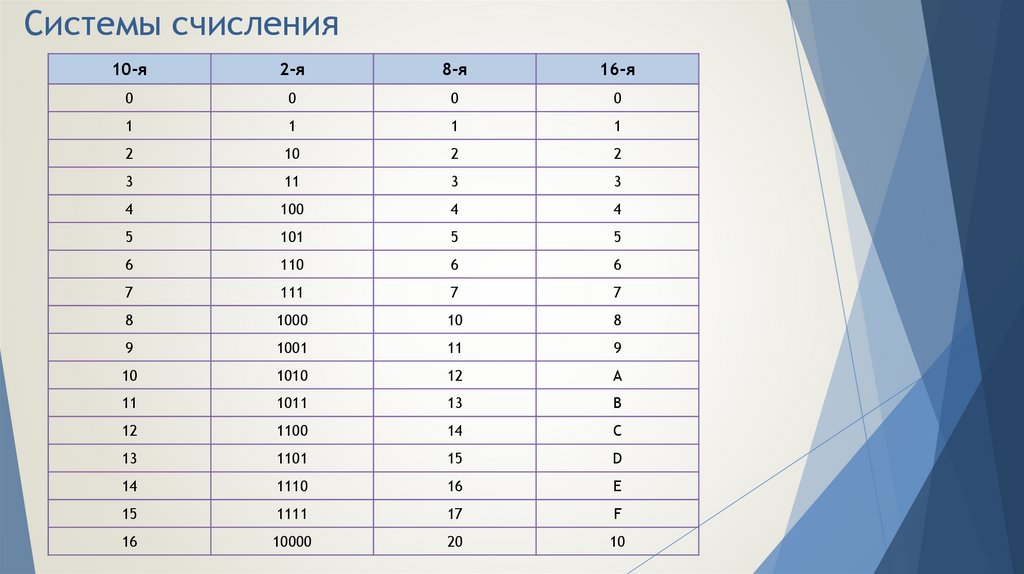
9. Системы счисления

10-я
2-я
8-я
16-я
0
0
0
0
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10

10. Примеры

Десятичное
число
Двоичное число
Код прямой
двоичный 8-и
разрядный
Примечание
0
0
0000 0000
Положительный
ноль
-0
-0
1000 0000
Отрицательный
ноль
5
101
0000 0101
10
1010
0000 1010
-5
-101
1000 0101
-16
-10000
1001 0000
9/16
0.1001
0.100 1000
-9/16
-0.1001
1.100 1000
105/128
0.1101001
0.110 1001
-5/128
-0.0000101
1.000 0101

11. Дополнительный код

Дополнительный код - наиболее распространённый
способ представления отрицательных целых чисел в
компьютерах
Он позволяет заменить операцию вычитания на
операцию сложения и сделать операции сложения и
вычитания одинаковыми для знаковых и беззнаковых
чисел, чем упрощает архитектуру ЭВМ

12. Дополнительный код

Дополнительный код положительного числа
совпадает с его прямым кодом.
Дополнительный код целого отрицательного числа
может быть получен по следующему алгоритму:
записать
прямой код модуля числа;
инвертировать его (заменить единицы нулями,
нули — единицами);
прибавить к инверсному коду
единицу.

13. Примеры

Например, запишем дополнительный код числа
37, интерпретируя его как величину типа int
(тридцатидвухбитовое со знаком):
прямой
код числа 37 есть
00000000000000000000000000100101
инверсный
код
11111111111111111111111111011010
дополнительный
код
11111111111111111111111111011011 или FFFFFFDB(16)

14. Примеры

Запишем числа, соответствующие
дополнительным кодам:
0000000000010111
Поскольку в старшем разряде записан нуль, то
результат будет положительным. Это код числа 23
1111111111000000
Здесь записан код отрицательного числа.
Исполняем алгоритм:
1) 1111111111000000(2) - 1(2) = 1111111110111111(2)
2) 0000000001000000
3) 1000000(2) = 64(10)
Ответ: -64

15. Практикум

Запишите прямой код десятичного числа 110, интерпретируя
как восьмибитовое целое без знака.
0110 1110
Запишите дополнительный код десятичного числа -104,
интерпретируя как восьмибитовое целое со знаком.
1001 1000
Запишите прямой код десятичного числа 4934,
интерпретируя как шестнадцатибитовое целое без знака.
000 10011 0100 0110
Запишите дополнительный код десятичного числа -29695,
интерпретируя как шестнадцатибитовое целое со знаком.
1000 1100 0000 0001

16. Практикум

Запишите в десятичной системе счисления целое число,
если дан его дополнительный код: 0010 0001 0010 1110
8494
Запишите в десятичной системе счисления целое число,
если дан его дополнительный код: 1110 0111 1011 0100
-6220
Даны два числа 45 и -76. Интерпретируя их как
восьмибитовые целые со знаком найти сумму.
45 = 00101101
-76 = 10110100
00101101 + 10110100 = 11100001
11100001 -> 11100000 -> 00011111 -> 3110 -> -31

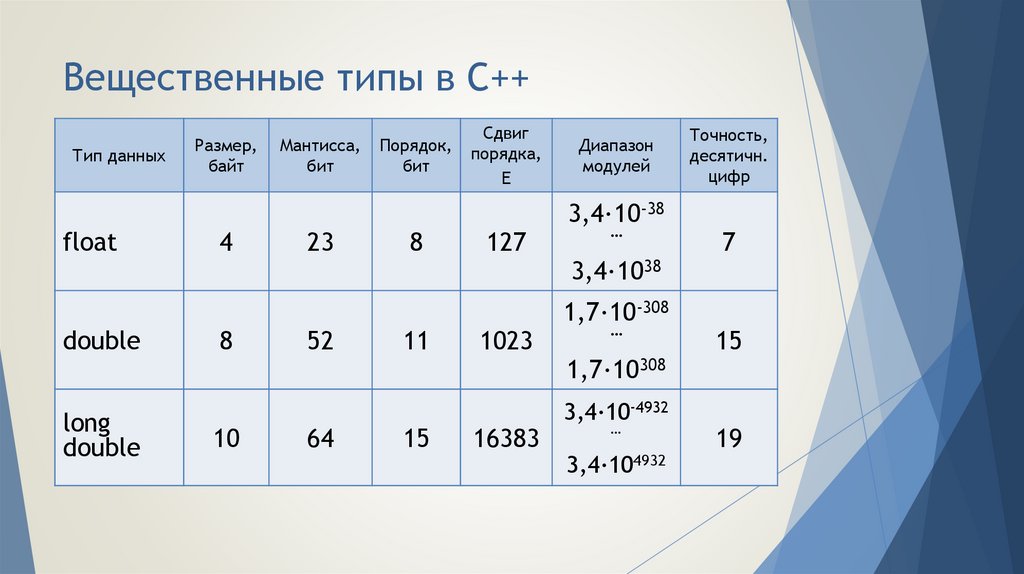
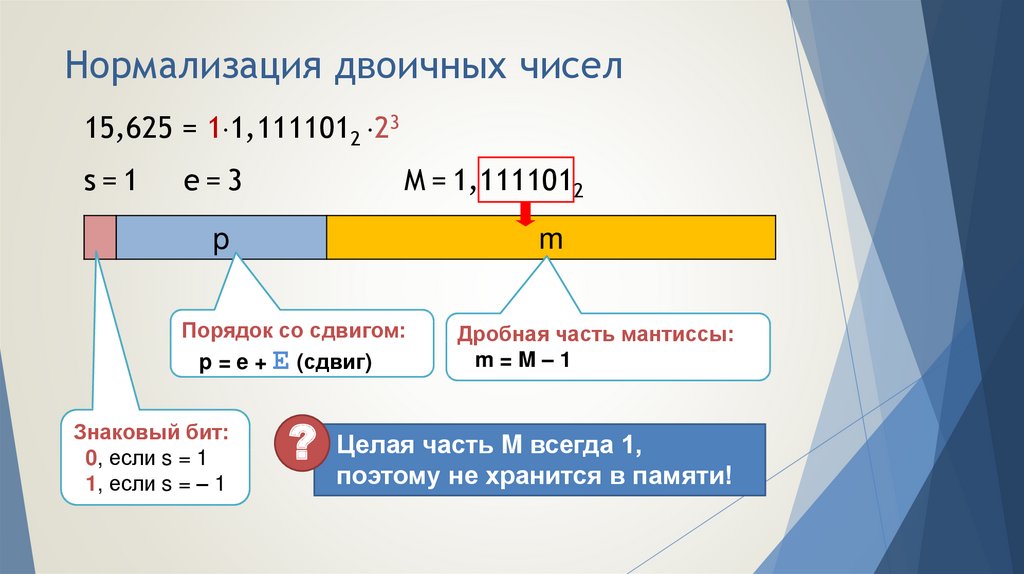
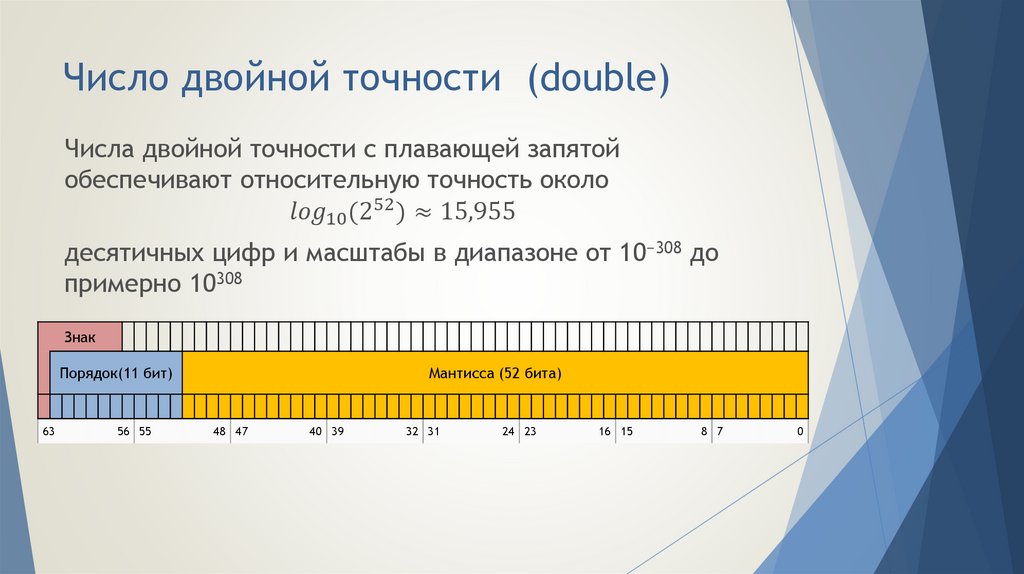
17. Вещественные типы в С++

Тип данных
float
double
long
double
Размер,
байт
4
8
10
Мантисса,
бит
23
52
64
Порядок,
бит
8
11
15
Сдвиг
порядка,
E
127
1023
16383
Диапазон
модулей
3,4·10-38
…
3,4·1038
1,7·10-308
…
1,7·10308
3,4·10-4932
…
3,4·104932
Точность,
десятичн.
цифр
7
15
19

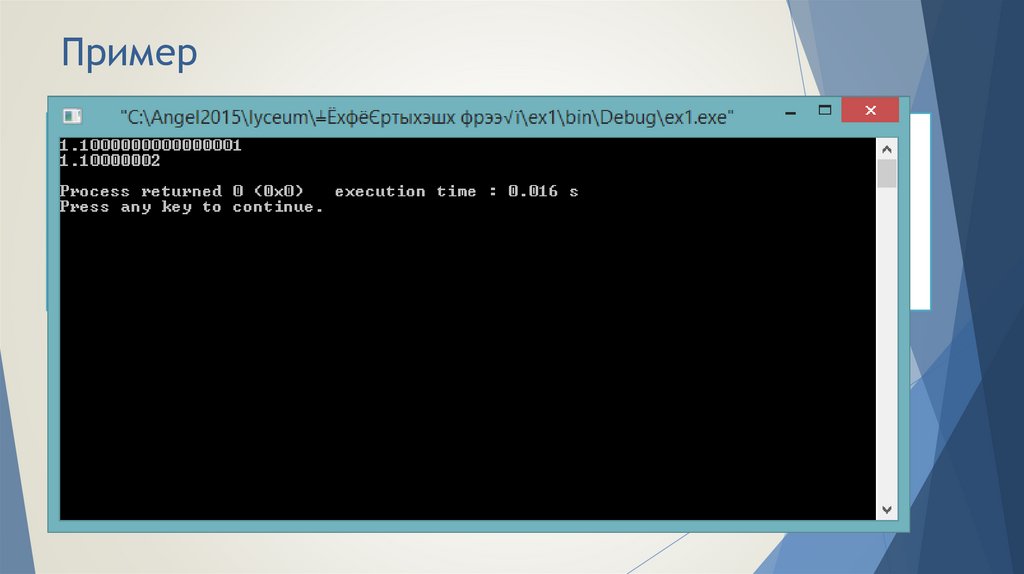
18. Пример

double f = 0.0;
float ff = 0.0;
for (int i=1; i <= 10; i++)
for (int i=1; i <= 10; i++)
f += 0.11;
ff += 0.11;
cout<<fixed;
cout<<fixed;
cout<<setprecision(16)<<f<<endl;
cout<<setprecision(8)<<ff<<endl;

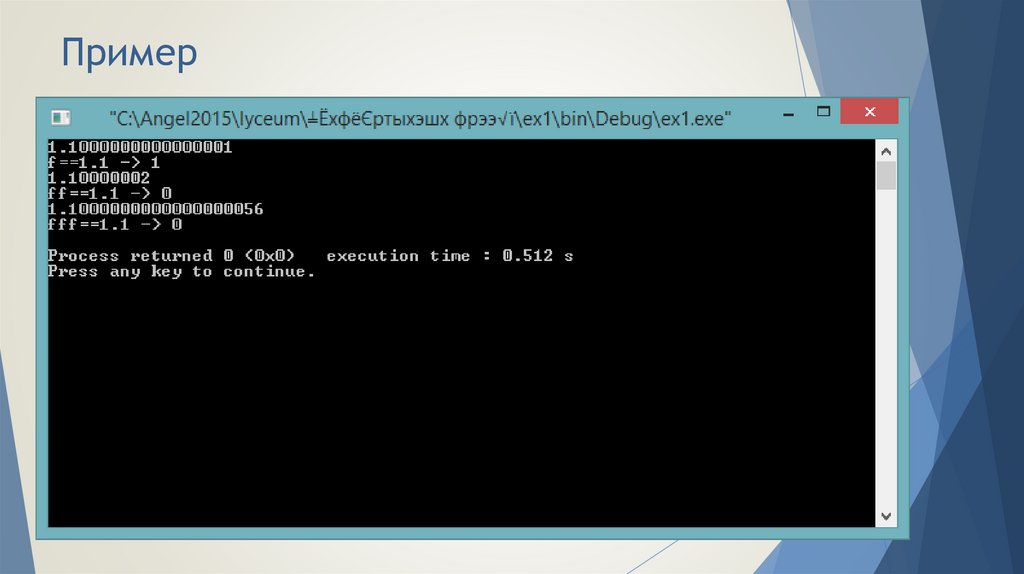
19. Пример

long double fff = 0.0;
for (int i=1; i <= 10; i++)
fff += 0.11;
cout <<fixed;
cout << setprecision(19) << fff << endl;
cout << "fff==1.1 -> " << (fff==1.1) << endl;

20. Число одинарной точности (float)

Числа одинарной точности с плавающей запятой
обеспечивают относительную точность около