Линейное уравнение с двумя переменными и его график

1.

2.

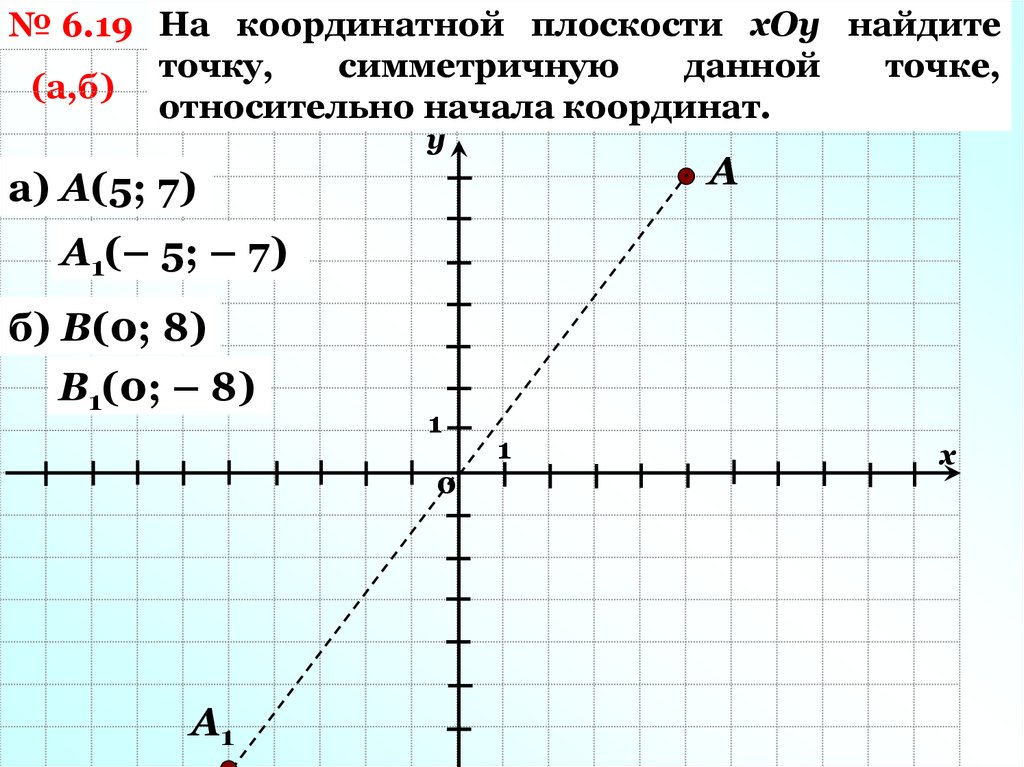
№ 6.19 На координатной плоскости хОу найдите
точку,
симметричную
данной
точке,
(а,б)
относительно начала координат.
у
А
а) А(5; 7)
А1(– 5; – 7)
б) В(0; 8)
В1(0; – 8)
1
0
А1
1
х

3.

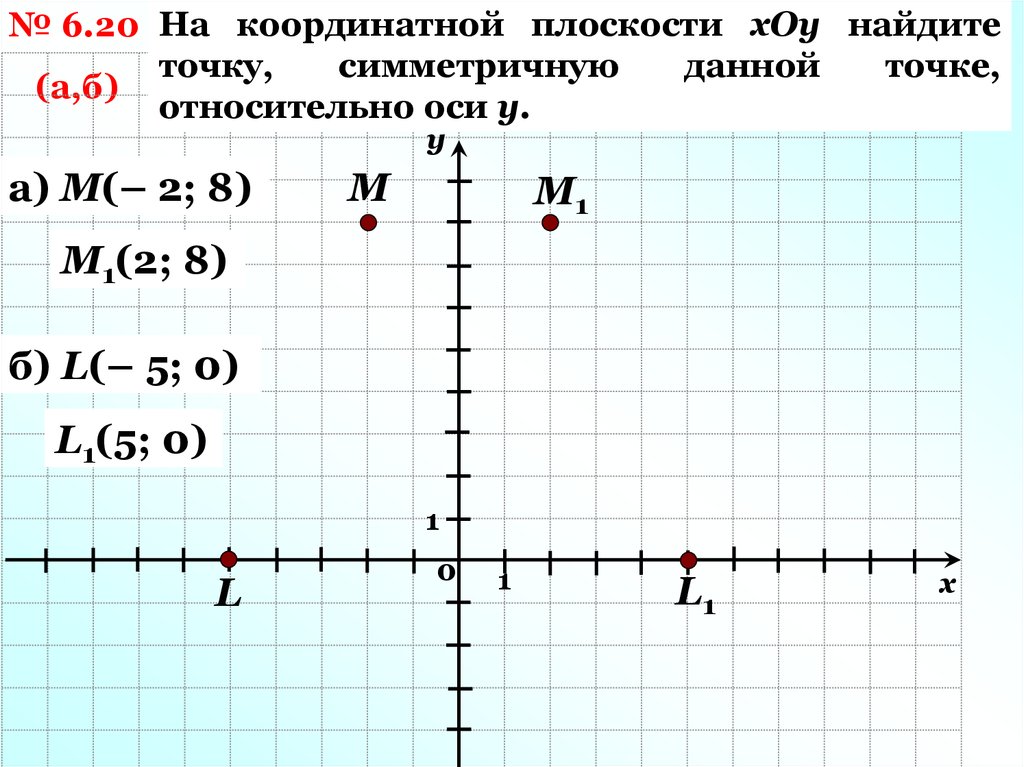
№ 6.20 На координатной плоскости хОу найдите
точку,
симметричную
данной
точке,
(а,б)
относительно оси у.
у
а) М(– 2; 8)
М
М1
М1(2; 8)
б) L(– 5; 0)
L1(5; 0)
1
L
0
1
L1
х

4.

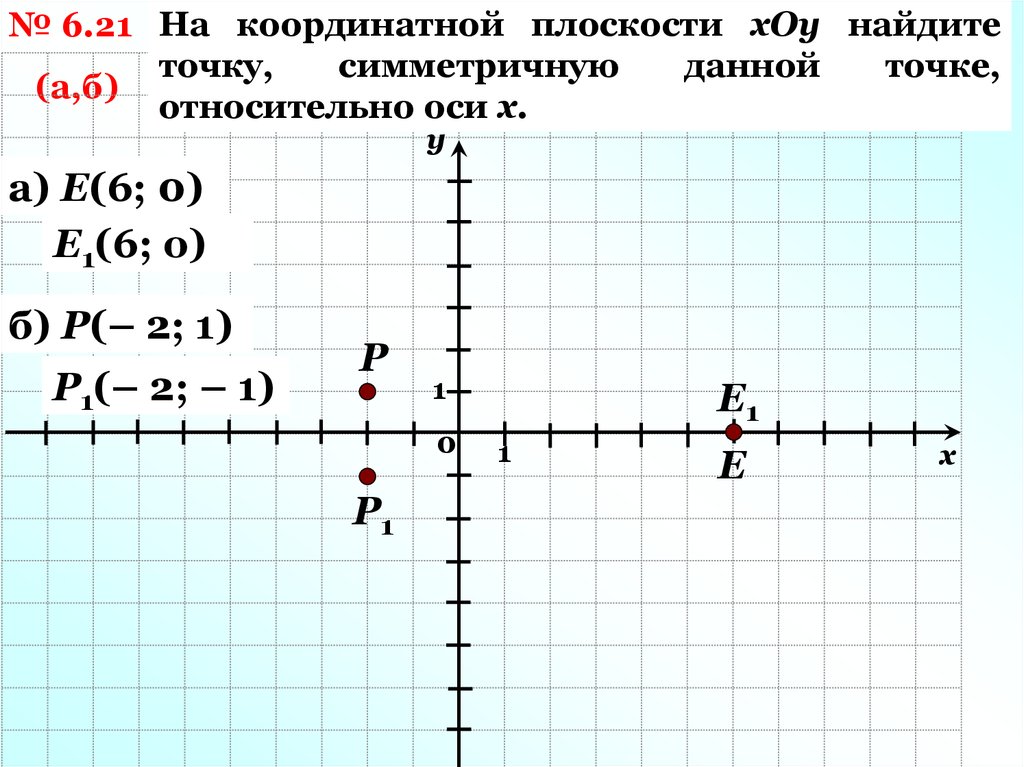
№ 6.21 На координатной плоскости хОу найдите
точку,
симметричную
данной
точке,
(а,б)
относительно оси х.
у
а) Е(6; 0)
Е1(6; о)
б) Р(– 2; 1)
Р1(– 2; – 1)
Р
1
0
Р1
Е1
1
Е
х

5.

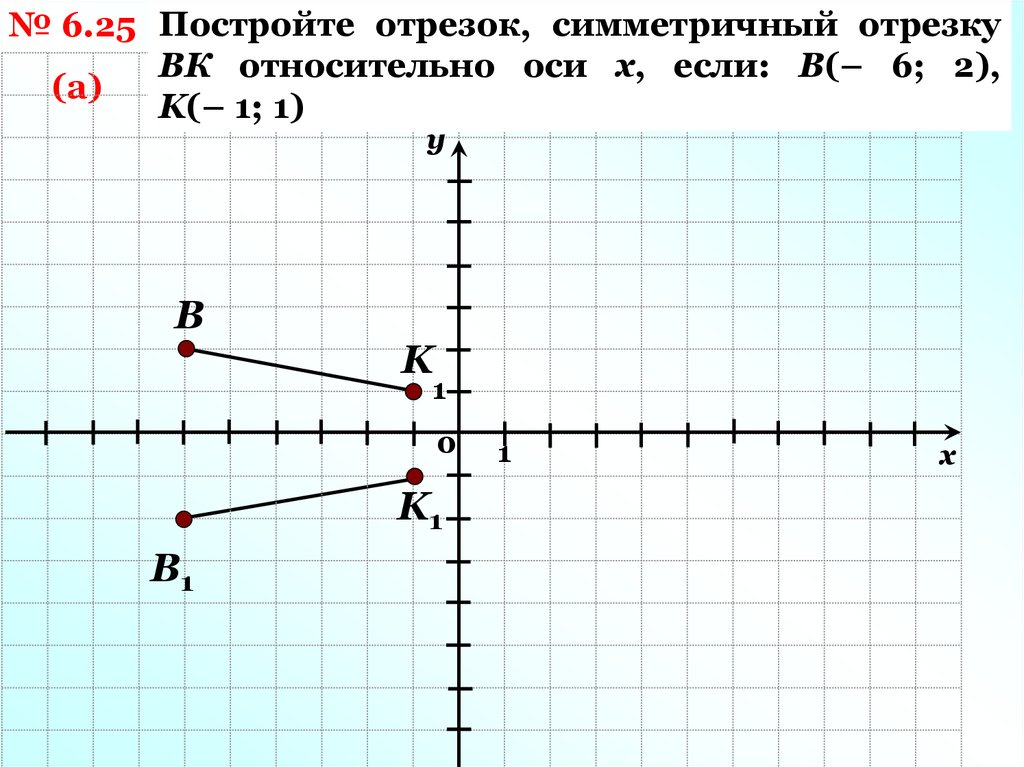
№ 6.25 Постройте отрезок, симметричный отрезку
ВК относительно оси х, если: В(– 6; 2),
(а)
K(– 1; 1)
у
В
K
1
0
K1
В1
1
х

6.

№ 6.26 Постройте отрезок, симметричный отрезку DM
относительно оси у, если: D(4; 2), М(1; 6)
(а)
М1
D1
у
М
D
1
0
1
х

7.

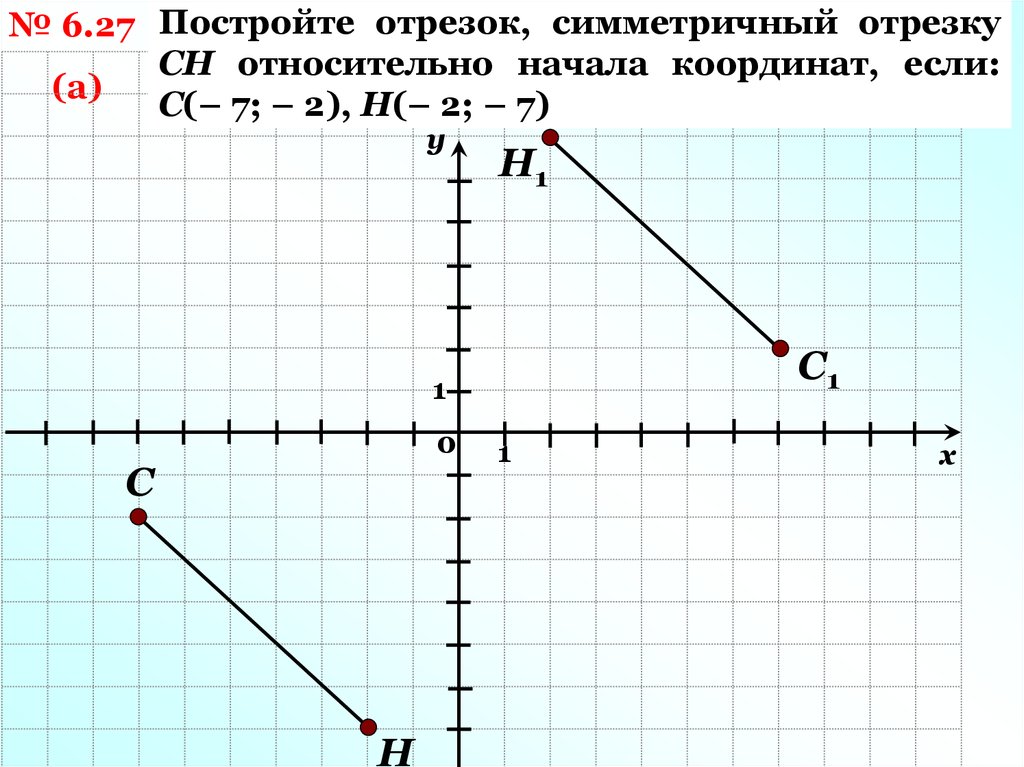
№ 6.27 Постройте отрезок, симметричный отрезку
СН относительно начала координат, если:
(а)
С(– 7; – 2), Н(– 2; – 7)
у
Н1
С1
1
0
С
Н
1
х

8.

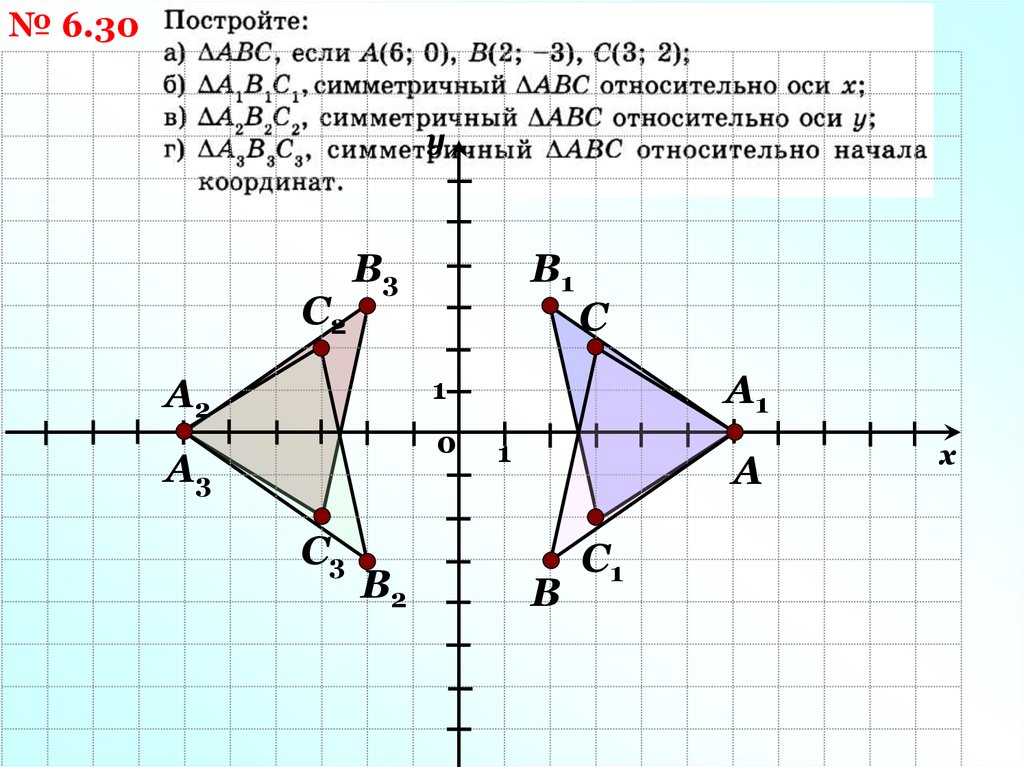
№ 6.30
у
С2
В3
А2
В1
С
А1
1
0
А3
С3
В2
1
А
В
С1
х

9.

02.10.2019
К л а с с н а я р а б о т а.
Линейное уравнение с двумя
переменными и его график

10.

РТ № 7.2 Составьте аналитическую модель
данной ситуации – уравнение.
а) Мастер в час делает k деталей, а ученик –
15. Мастер работал 4 ч, а ученик только 1
ч. Всего они сделали 135 деталей.
4k + 15 = 135
Сколько переменных содержит полученное
уравнение?
одну

11.

РТ № 7.1 Запишите в общем виде линейное
уравнение с одной переменной:
ах + b = 0

12.

РТ № 7.2 Составьте аналитическую модель
данной ситуации – уравнение.
б) 1 кг винограда стоит х р., а 1 кг абрикосов
у р. Боря купил 3 кг винограда и 5 кг абрикосов, заплатив за всю покупку 950 р.
3х + 5у = 950
Сколько переменных содержит полученное
уравнение?
две

13.

РТ № 7.2 Составьте аналитическую модель
данной ситуации – уравнение.
в) Площадь квадрата со стороной р больше
площади квадрата со стороной q на 34 см2
р2 – q2 = 34
Сколько переменных содержит полученное
уравнение?
две

14.

РТ № 7.5 Подчеркните те уравнения, которые
являются линейными уравнениями с
двумя переменными:
х – у + 4 = 0;
2х – 3у – 4 = 0;
2х + 3у = 4;
а + b + с = 0;
5m2 – 25n – 10 = 0.

15.

РТ № 7.2 Составьте аналитическую модель
данной ситуации – уравнение.
б) 1 кг винограда стоит х р., а 1 кг абрикосов
у р. Боря купил 3 кг винограда и 5 кг абрикосов, заплатив за всю покупку 950 р.
3х + 5у = 950
Мог ли 1 кг винограда стоить 100 р., а 1 кг
абрикосов – 130 р?
3 · 100 + 5 · 130 = 950 да
Мог ли 1 кг винограда стоить 150 р., а 1 кг
абрикосов – 120 р?
3 · 150 + 5 · 120 = 950 нет

16.

3х + 5у = 950
х = 100, у = 130
3 · 100 + 5 · 130 = 950 верно
х = 150, у = 120
3 · 150 + 5 · 120 = 950 неверно
х = 100, у = 130 или (100; 130) – решение уравнения

17.

РТ № 7.6 Проверьте, является ли решением
уравнения 3х + у – 7 = 0 пара чисел:
а) (1; 4)
3·1+4–7=0
0 = 0 является
б) (– 2; 13)
3 · (– 2) + 13 – 7 = 0
0 = 0 является
в) (1; – 100)
3 · 1 + (– 100) – 7 = 0
– 104 = 0
г) (5; – 8)
не является
3 · 5 + (– 8) – 7 = 0
0 = 0 является

18.

РТ № 7.6
Найдите ещё какие-нибудь решения уравнения 3х + у – 7 = 0.
РТ № 7.7
Запишите, сколько решений имеет линейное уравнение с двумя переменными:
бесконечное количество

19.

№ 7.10(б) Для
данного
линейного
уравнения
найдите значение y, соответствующее
заданному значению x.
5x – 7y – 14 = 0, если x = 0
если x = 0, то 5 · 0 – 7y – 14 = 0
– 7y – 14 = 0
– 7y = 14
y=–2
Ответ: y = – 2

20.

№ 7.11(б) Для
данного
линейного
уравнения
найдите значение y, соответствующее
заданному значению x.
11x – 13y + 16 = 0, если x = – 5
если x = – 5, то – 55 – 13y + 16 = 0
– 13y – 39 = 0
– 13y = 39
y=–3
Ответ: y = – 3

21.

№ 7.14(б) Для
данного
линейного
уравнения
найдите значение x, соответствующее
заданному значению y.
23x – 9y + 5 = 0, если y = – 2
если y = – 2, то 23x – 9 · (– 2) + 5 = 0
23x + 18 + 5 = 0
23x + 23 = 0
23x = – 23
x=–1
Ответ: x = – 1

22.

№ 7.25(а) Среди решений уравнения x + 3y – 20 = 0
найдите такую пару, которая состоит из
двух одинаковых чисел
если x = y, то y + 3y – 20 = 0
4y – 20 = 0
4y = 20
y=5
Ответ: (5; 5)

23.

№ 7.26(а) Найдите значение коэффициента a в
уравнении ax + 5y – 40 = 0, если известно,
что решением уравнения является пара
чисел (3; 2).
если x =3 y = 2, то a · 3 + 5 · 2 – 40 = 0
3a – 30 = 0
3a = 30
a = 10
Ответ: a = 10

24.

№ 7.27(а) Найдите значение коэффициента b в
уравнении 6x + by – 35 = 0, если известно,
что решением уравнения является пара
чисел (0; 1).
если x =0 y = 1, то 6 · 0 + b · 1 – 35 = 0
b – 35 = 0
b = 35
Ответ: b = 35

25.

У: стр. 39 § 7
З: § 7 № 6 – 8(а);
10 – 14(а).