Похожие презентации:
Понятия теории графов
1.
Граф состоит из множества вершин X и рёбер U.Вершины обозначают кружками, рёбра – прямыми линиями,
граф – буквой G.
Граф, содержащий n вершин и m рёбер, обозначается как
G ( X , Y ), X x1, x2 ,...xn , X n, U u1, u2 ,...um , U m
2.
X x1 , x2 , x3 , x4 ,X 4,
U u1 , u2 , u3 , u4 , u5 x1 , x2 , x2 , x3 , x3 , x4 , x4 , x2 , x1 , x4 , U 5
G
x1
x2
x4
x3
3.
Граф можно изображать по разному:x2
x2
x1
G
x2
x1
G
G
x1
Ребро графа соединяет две вершины, которые называются
смежными. Так, для ребра u3 смежными будут вершины x3 и x4.
Ребро u3 является инцидентным вершинам x3 и x4.
Степенью вершины xi (deg xi) графа G называется
число рёбер, инцидентных xi, i = 1, …, n.
deg x1 2, deg x2 3, deg x3 2, deg x4 3.
4.
Сумма степеней вершин графа G равнаудвоенному числу его рёбер:
n
deg x
i 1
i
2m
5.
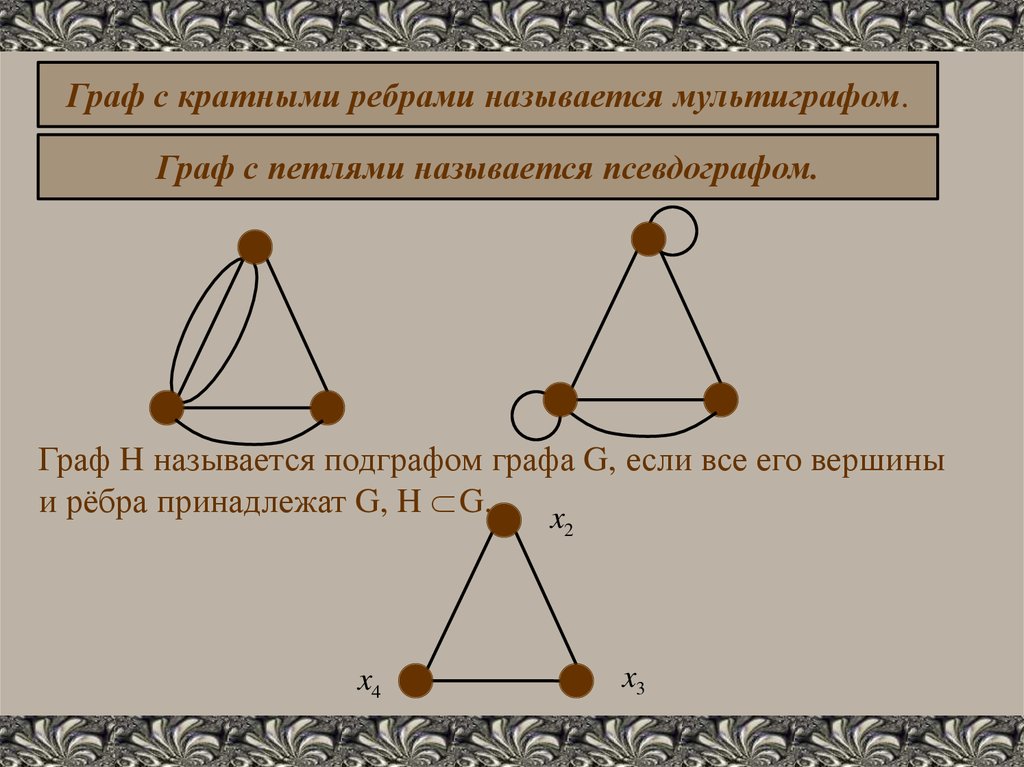
Граф с кратными ребрами называется мультиграфом.Граф с петлями называется псевдографом.
Граф H называется подграфом графа G, если все его вершины
и рёбра принадлежат G, H G.
x
2
x4
x3
6.
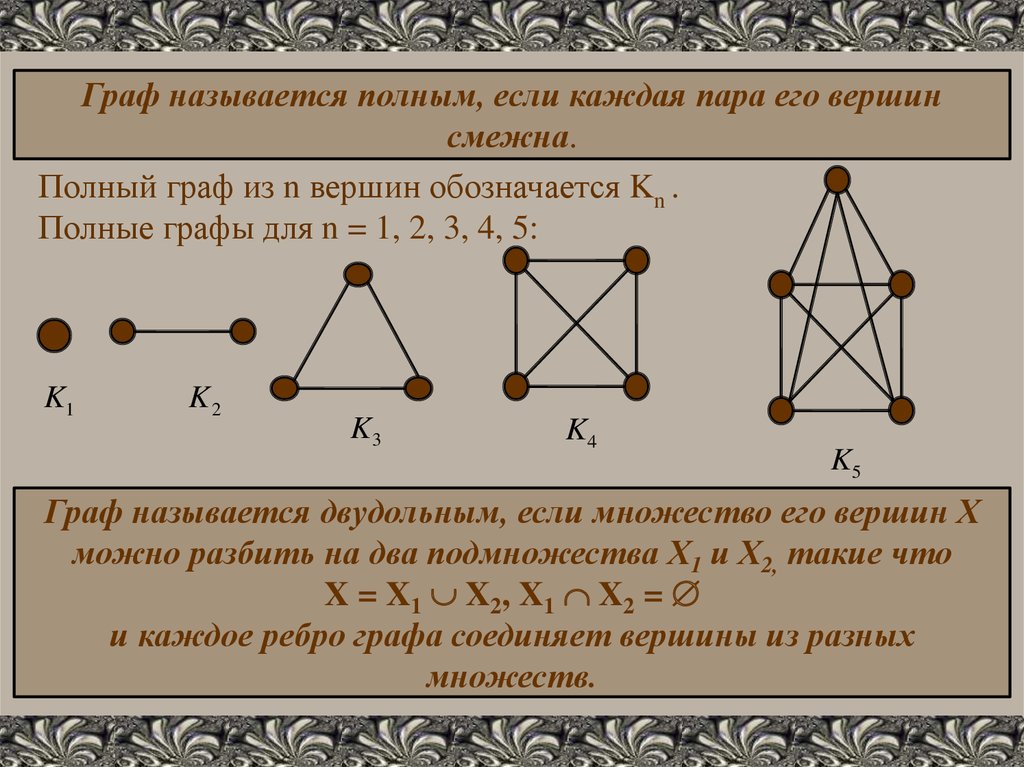
Граф называется полным, если каждая пара его вершинсмежна.
Полный граф из n вершин обозначается Kn .
Полные графы для n = 1, 2, 3, 4, 5:
K1
K2
K3
K4
K5
Граф называется двудольным, если множество его вершин X
можно разбить на два подмножества X1 и X2, такие что
X = X1 X2, X1 X2 =
и каждое ребро графа соединяет вершины из разных
множеств.
7.
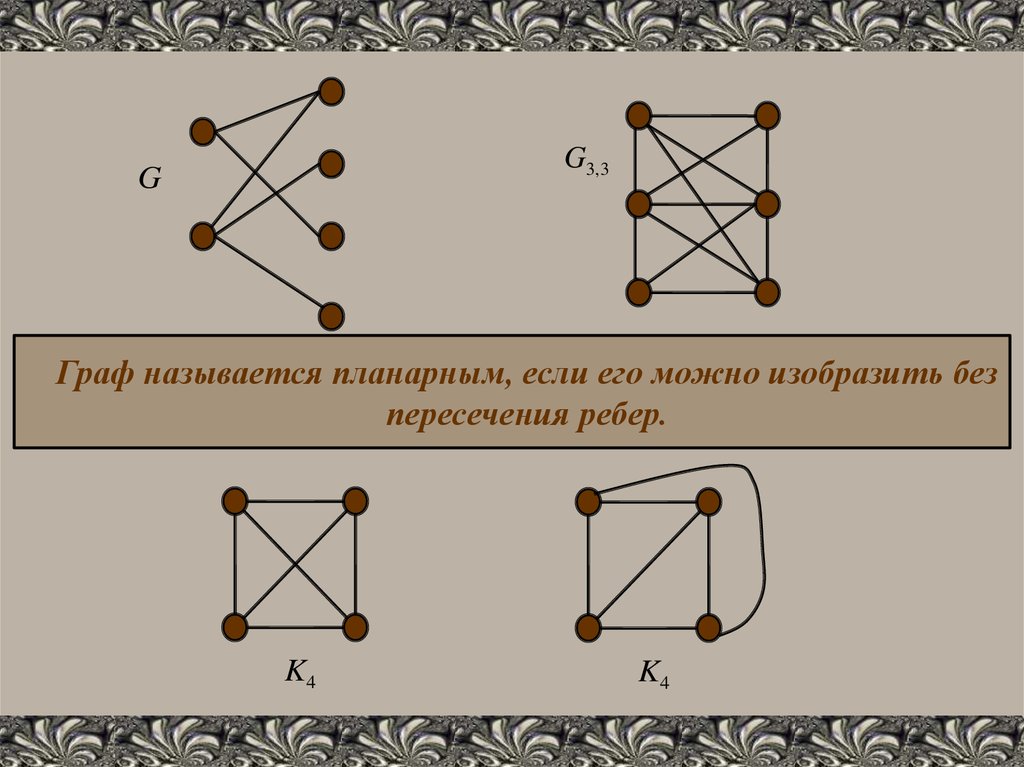
G3, 3G
Граф называется планарным, если его можно изобразить без
пересечения ребер.
K4
K4
8.
Маршрутом в графе G называется последовательностьсмежных вершин и рёбер.
Маршрут называется цепью, если все его рёбра различны.
Маршрут называется простой цепью, если все его вершины
(а, следовательно, и рёбра) различны.
Если в цепи начальная вершина совпадает с конечной, то она
называется циклом.
Если в простой цепи начальная вершина совпадает с конечной,
то она называется простым циклом.
9.
x1x2
x3
x5
x4
G
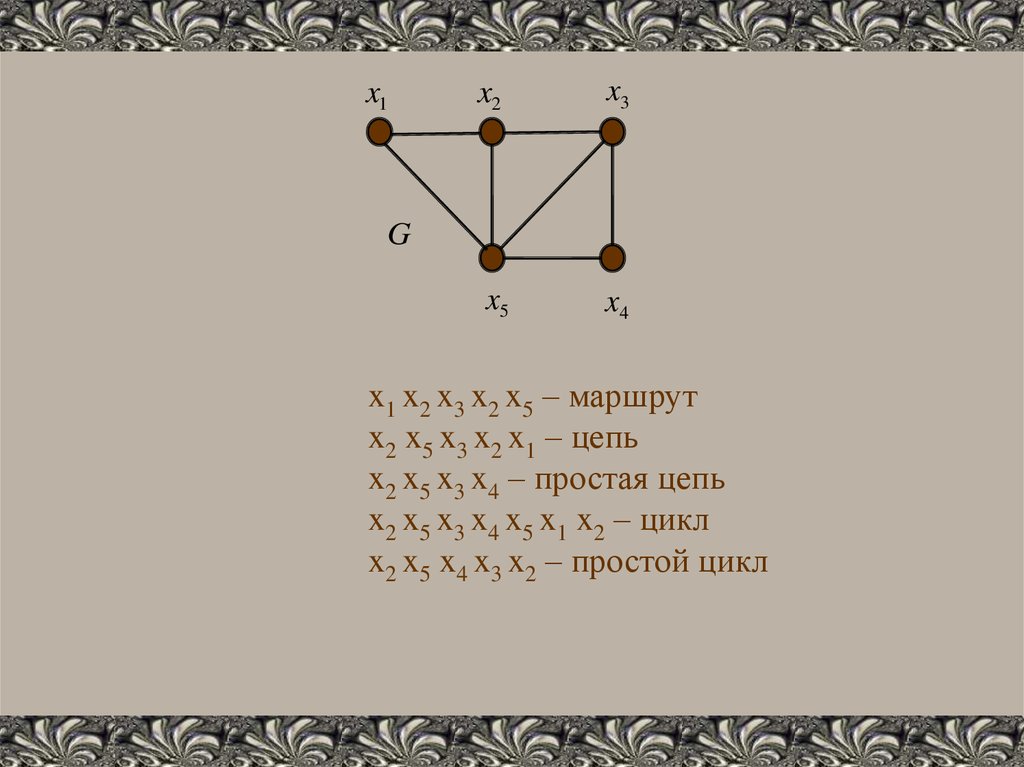
x1 x2 x3 x2 x5 – маршрут
x2 x5 x3 x2 x1 – цепь
x2 x5 x3 x4 – простая цепь
x2 x5 x3 x4 x5 x1 x2 – цикл
x2 x5 x4 x3 x2 – простой цикл
10.
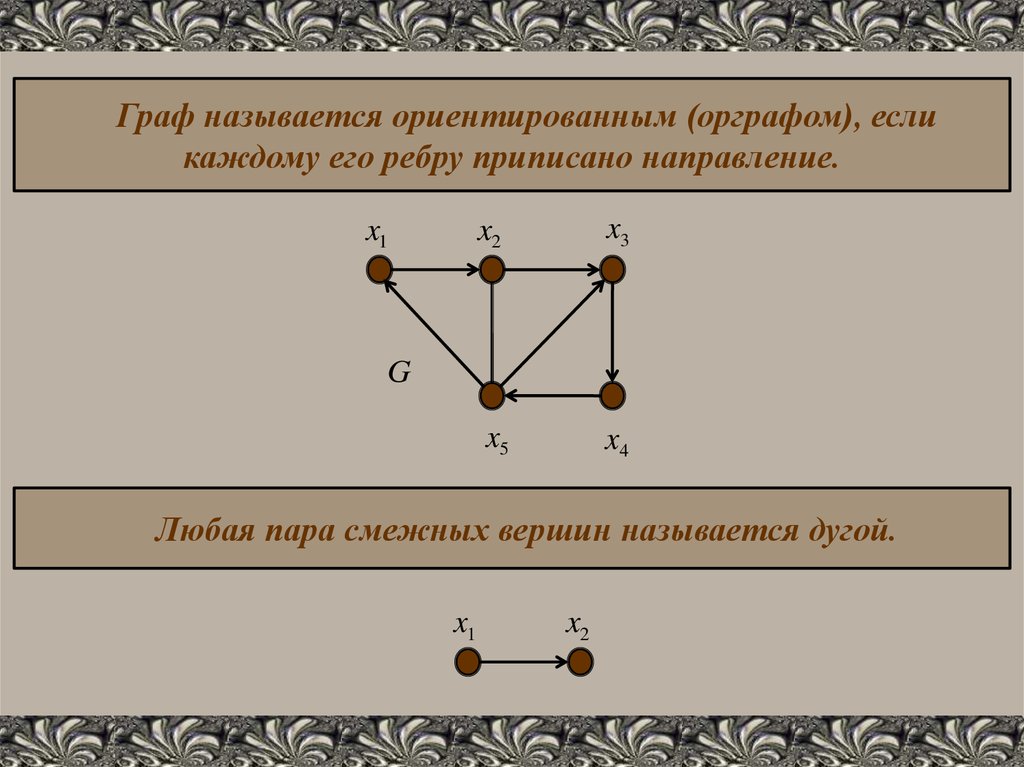
Граф называется ориентированным (орграфом), есликаждому его ребру приписано направление.
x1
x2
x3
x5
x4
G
Любая пара смежных вершин называется дугой.
x1
x2
11.
Полустепенью исхода od(x) называется число вершин,смежных из x.
Полустепенью захода id(y) называется число вершин,
смежных к y.
Ориентированным маршрутом в орграфе называется
чередующаяся последовательность смежных вершин и
дуг, которая начинается и оканчивается вершиной.
Маршрут, в котором все вершины различны,
называется путём.
Если путь имеет начальную вершину, совпадающую с
конечной, то он называется контуром.
12.
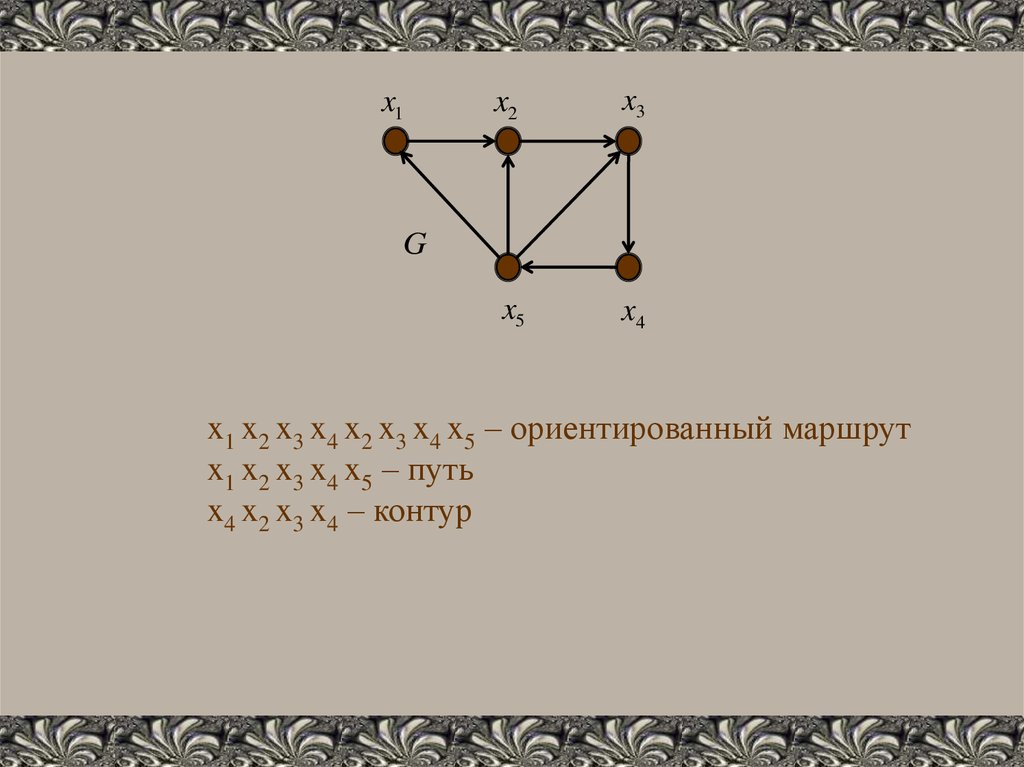
x1x2
x3
x5
x4
G
x1 x2 x3 x4 x2 x3 x4 x5 – ориентированный маршрут
x1 x2 x3 x4 x5 – путь
x4 x2 x3 x4 – контур
13.
Длина маршрута (цепи, простой цепи, цикла, простогоцикла, ориентированного маршрута, пути, контура) d
равна числу входящих в него рёбер (дуг).
d(x1 x2 x3 x4 x5) = 4
d(x4 x2 x3 x4) = 3
Поставим в соответствие каждому ребру графа G неотрицательное
число wj ≥ 0, j = 1, …, m.
G(X, U, W) – взвешенный граф, где X = {xi}, i = 1, …, n;
U = {uj}, j = 1, …, m; W = {wj}, j = 1, …, m.
14.
x2x1
6
5
2
3
x4
4
2
x3
G
X = {x1, x2, x3, x4};
U={(x1, x2), (x1, x3), (x1, x4), (x2, x3), (x2, x4), (x3, x4)};
W = {3, 2, 2, 5, 4, 6}.








 Математика
Математика








