Математическая модель. Свободное падение с учетом сопротивления среды

1. Математическая модель

Свободное падение с учетом
сопротивления среды
Глава 3.2
§3.2.2
11 класс

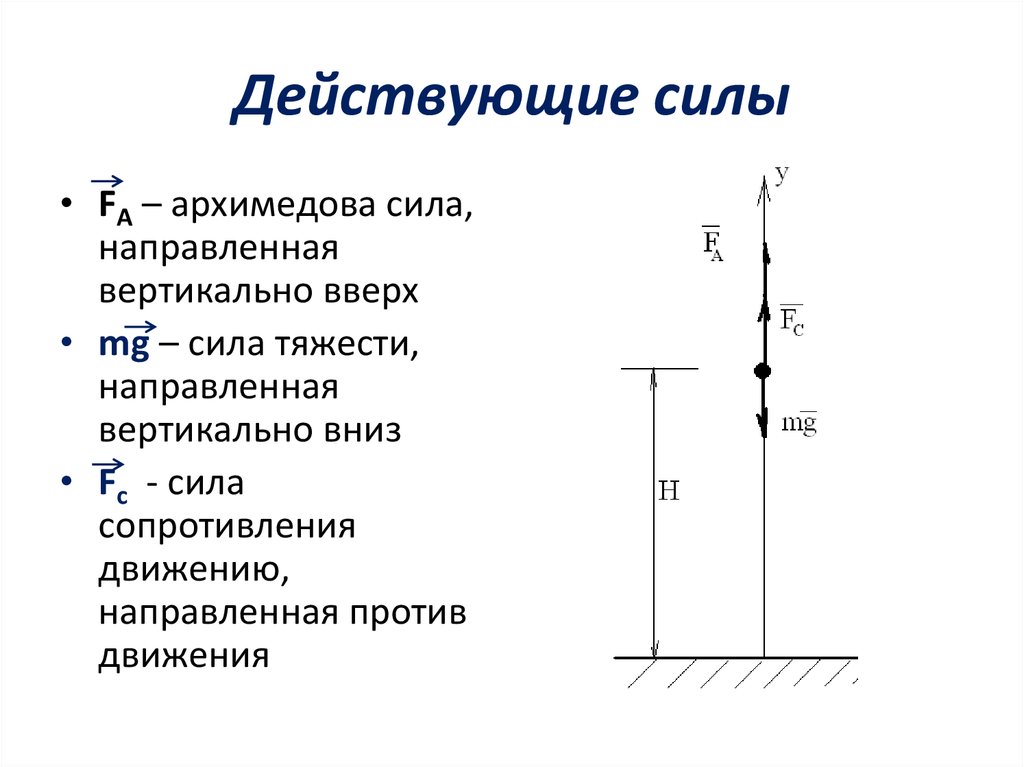
2. Действующие силы

• FА – архимедова сила,
направленная
вертикально вверх
• mg – сила тяжести,
направленная
вертикально вниз
• Fс - сила
сопротивления
движению,
направленная против
движения

3. Анализ объекта

• Архимедова сила
FА < mg
(плотность газа много
меньше плотности тела,
но плотность воды
следует учесть)
пренебрегаем
• Сила сопротивления
среды
Зависит от плотности
среды и зависит от
скорости, но…
Очевидно, что на
предмет, падающий с
большой высоты,
действует Fс
увеличивающаяся по
мере роста скорости v

4. Сила сопротивления F

Сила сопротивления Fc
• V – малая – преобладает вязкое трение
жидкости или газа
Fc пропорциональна V
• С ростом V – возрастает лобовое
сопротивление (парусный эффект)
F пропорциональна V2
c
Fc = k 1∙ v + k 2∙ v 2

5. Математическая формализация

Из уравнения закона Ньютона
• ma = mg + FА + Fс
Проектируем данное векторное уравнение
на ось Y
Fс (t)- mg k1 v(t) + k2 v(t) 2- mg
• a(t) =
=
Ф1*
m
m

6. Численный подход к моделированию процессов

vi+1 – vi
a=
Δt
Δ
t – малый шаг изменения времени
• vi+1 = vi + ai Δ t
Из Ф1* выразим ai
k1 v(t) + k2 v(t)2 – mg
Δt
vi+1 = vi +
m

7. Численный подход к моделированию процессов

yi+1 = yi + vi Δ t
- координата y,
где i = 0,1,2,…
По условию задачи падение происходит с высоты Н
с нулевой начальной скоростью =>
v(0) = v0 = 0
y(0) = y0 = Н

8. Математическая модель

• Исходные данные
v(0) = v0 = 0
y(0) = y0 = Н
• Рекуррентные формулы
2
k1 v(t) + k2 v(t) – mg
Δ t
vi+1 = vi +
m
yi+1 = yi + vi Δ t

9.

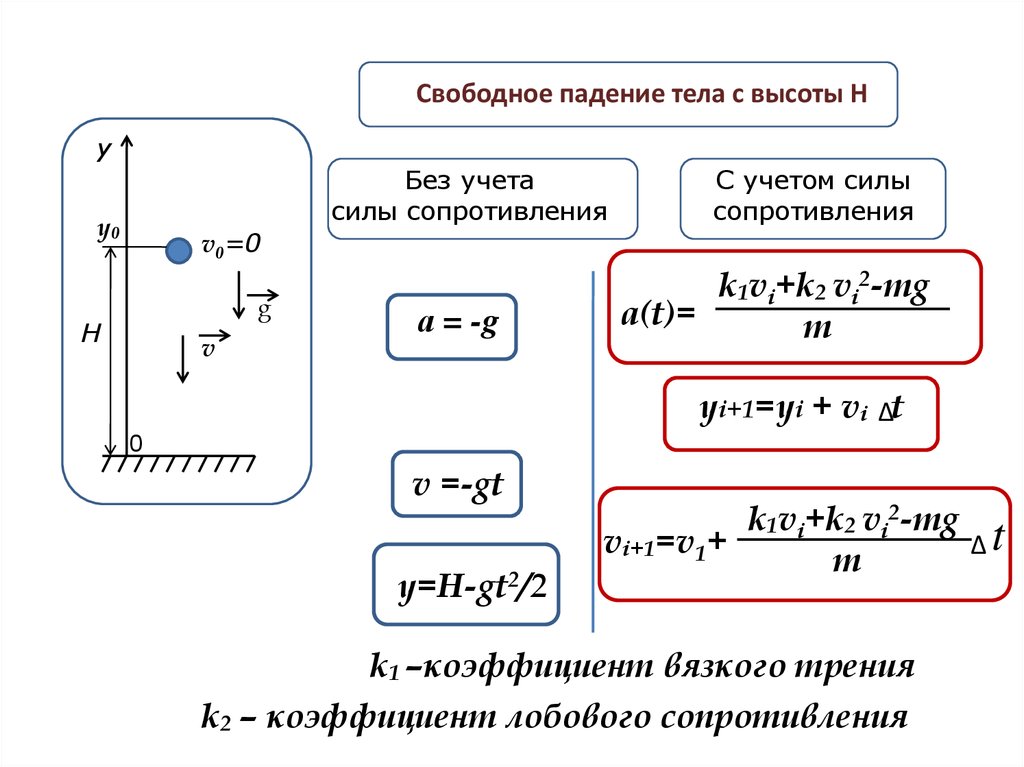
Свободное падение тела с высоты H
у
Без учета
силы сопротивления
y0
С учетом силы
сопротивления
v0=0
g
H
v
а = -g
k1vi+k2 vi2-mg
a(t)=
m
yi+1=yi + vi Δt
0
v =-gt
yy=H-gt
=y0-gt2/2 2/2
k1vi+k2 vi2-mg
vi+1=v1+
Δt
m
k1 –коэффициент вязкого трения
k2 – коэффициент лобового сопротивления

10. Предельная скорость свободного падения

• С возрастанием скорости падения v
возрастает сила сопротивления Fc =>
Fc – mg уменьшается.
• Когда Fc = mg, скорость выйдет на
постоянное предельное значение v*.
• Находим из уравнения
k1 v + k2 v 2 – mg = 0

11. Параметры модели

• Определим k1 для конкретных ситуаций.
• k1 – пропорциональная динамической вязкости
среды (μ)
• k1 = с1 ∙μ∙ b
• с1 – определяется формой тела
• b – характерный размер тела в направлении,
│ потоку, обтекающего газа или жидкости.
Для тела сферической формы k1 = 6π ∙ μ ∙ r

12. Параметры модели

• Определим k2 для конкретных ситуаций
• k2 пропорциональна площади поперечного
сечения тела δ, плотности среды ρ, и
зависит от формы тела.