Похожие презентации:
Специальные главы математики. Образовательная программа
1.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное автономное образовательное учреждение
высшего образования
«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»
УТВЕРЖДАЮ
Проректор по учебной работе
___________________ С.Т. Князев
«___» _________________ 201 г.
РАБОЧАЯ ПРОГРАММА МОДУЛЯ
СПЕЦИАЛЬНЫЕ ГЛАВЫ МАТЕМАТИКИ
Перечень сведений о рабочей программе модуля
Модуль
Специальные главы математики
Образовательная программа
Прикладная математика
Траектория образовательной программы (ТОП)
Направление подготовки
Прикладная математика
Уровень подготовки
Бакалавриат
ФГОС ВО
Екатеринбург, 2017
Учетные данные
Код модуля 1127561
Код ОП
01.03.04/01.01
Учебные план в ЕИСУ
№ 6104
Не предусмотрено
Код направления и
подготовки
01.03.04
уровня
Реквизиты приказа Минобрнауки
РФ об утверждении ФГОС ВО:
12 марта 2015 г., № 208
2.
Программа модуля составлена авторами:№ п/п
ФИО
1
Сесекин
Александр
Николаевич
Гредасова
Надежда
Викторовна
2
Ученая степень,
ученое звание
Д-р. физ.-мат. наук,
профессор
Канд. физ.-мат.
наук
Руководитель модуля
Должность
Кафедра
Подпись
Профессор
Прикладная
математика
Доцент
Прикладная
математика
А.Н. Сесекин
Рекомендовано учебно-методическим советом Уральского энергетического института
Председатель учебно-методического совета
Протокол № ______ от __________ г.
Е.В. Черепанова
Согласовано:
Дирекция образовательных программ
Р.Х. Токарева
Руководитель образовательной программы (ОП),
для которой реализуется модуль
2
Н.В. Гредасова
3.
1. ОБЩАЯ ХАРАКТЕРИСТИКА МОДУЛЯ Специальные главы математики1.1. Объем модуля, 28 з.е.
1.2. Аннотация содержания модуля
Модуль относиться к базовой части.
Модуль посвящен изучению теорем и методов решения задач из следующих разделов
математики: обыкновенные дифференциальные уравнения, теория устойчивости, теория
вероятностей, математическая статистика, теория функций комплексного переменного,
операционное исчисление, дискретная математика, функциональный анализ. Рассматривается
понятие вычислительного эксперимента как метода исследования, а также математические
модели в естествознании, теплоэнергетике, медицине, экономике, гуманитарных науках.
Дисциплины модуля: Теория вероятностей и математическая статистика,
Обыкновенные дифференциальные уравнения и теория устойчивости, Теория функций
комплексного переменного и операционное исчисление, Дискретная математика,
Функциональный анализ, Введение в специальность.
2. СТРУКТУРА МОДУЛЯ И РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО
ДИСЦИПЛИНАМ
Объем времени, отведенный на освоение дисциплин модуля
Промеж
уточная
аттестац
ия
(зачет,
экзамен)
, час.
Зач. ед.
Самосто
ятельна
я
работа,
включа
я все
виды
текущей
аттестац
ии, час.
Всего по
дисципли
не
Час.
Всего
Лабораторные работы
Практические занятия
Аудиторные занятия, час.
Лекции
Семестр изучения
Наименования дисциплин с
указанием, к какой части
образовательной программы
они относятся: базовой (Б),
вариативной – по выбору вуза
(ВВ), вариативной - по выбору
студента (ВС).
Возможными комбинациями
дисциплин в модуле могут быть:
Б-Б; Б-ВВ; ВВ-ВВ; ВС-ВС
1.
(Б) Функциональный
анализ
4
34
17
51
53
З,4
10
8
3
2.
(Б) Обыкновенные
дифференциальные
уравнения и теория
устойчивости
(Б) Теория функций
комплексного
переменного и
операционное
исчисление
(Б) Дискретная
математика
3
34
34
68
58
Э,18
4
4
17
17
34
34
З,4
14
4
72
3
34
17
51
75
Э,18
14
4
4
3
17
34
51
89
З,4
4
4
34
34
68
58
Э,18
3
17
17
34
70
З,4
4
34
34
68
58
Э,18
14
4
14
4
10
8
14
4
3.
4.
5.
6.
(Б) Введение в
специальность
(Б) Теория
вероятностей и
математическая
3
2
4
3
4
4.
статистикаВсего на освоение модуля
221
204
425
495
88
10
08
2
8
3. ПОСЛЕДОВАТЕЛЬНОСТЬ ОСВОЕНИЯ ДИСЦИПЛИН В МОДУЛЕ
Последовательность освоения дисциплин
3.1. Пререквизиты и постреквизиты в
указана в таблице 2.
модуле
3.2. Кореквизиты
4. ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ МОДУЛЯ
4.1. Планируемые результаты освоения модуля и составляющие их компетенции
Коды ОП,
Планируемые в
Компетенции в
Универсальн
для которых ОХОП результаты
соответствии с ФГОС ВО,
ые
реализуется
обучения -РО,
а также дополнительные из
компетенции
модуль
которые
ОХОП, формируемые при
(УОК,
формируются при
освоении модуля
УОПК,УПК),
освоении модуля
формируемые
при освоении
модуля
для
нескольких
ОП
01.03.04/01.01 РО1: способность в ОПК-1 - готовность к
рамках научносамостоятельной работе;
исследовательской
ОПК-2 - способность использовать
деятельности
современные математические
разрабатывать и
методы и современные прикладные
исследовать
программные средства и осваивать
математические
современные технологии
модели
программирования;
ПК-9 - способность выявить
естественнонаучную сущность
проблем, возникающих в ходе
профессиональной деятельности,
готовностью использовать для их
решения соответствующий
естественнонаучный аппарат;
ПК-10 - готовность применять
математический аппарат для
решения поставленных задач,
способностью применить
соответствующую процессу
математическую модель и
проверить ее адекватность,
провести анализ результатов
моделирования, принять решение
на основе полученных результатов;
ПК-12 - способность
самостоятельно изучать новые
разделы фундаментальных наук.
01.03.04/01.01 РО3: способность в ОПК-1 - готовность к
рамках научносамостоятельной работе;
4
5.
исследовательскойи производственнотехнологической
деятельности
осуществлять сбор,
обработку и анализ
результатов
теоретических или
экспериментальных
исследований
ОПК-2 - способность использовать
современные математические
методы и современные прикладные
программные средства и осваивать
современные технологии
программирования;
ПК-10 - готовность применять
математический аппарат для
решения поставленных задач,
способностью применить
соответствующую процессу
математическую модель и
проверить ее адекватность,
провести анализ результатов
моделирования, принять решение
на основе полученных результатов;
ПК-11 - готовность применять
знания и навыки управления
информацией.
4.2.Распределение формирования компетенций по дисциплинам модуля
Дисциплины модуля
1 (Б)
Функциональный
анализ
2 (Б) Обыкновенные
дифференциальные
уравнения. Теория
устойчивости
3 (Б) Теория функций
комплексного
переменного и
операционное
исчисление
4 (Б) Дискретная
математика
5 (Б) Введение в
специальность
6 (Б) Теория
вероятностей и
математическая
статистика
ОПК1
ОПК2
ПК9
ПК10
ПК11
ПК12
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
5. ПРОМЕЖУТОЧНАЯ АТТЕСТАЦИЯ ПО МОДУЛЮ
5.1. Весовой коэффициент значимости промежуточной аттестации по модулю:
5.2. Форма промежуточной аттестации по модулю:
Не предусмотрена
5.3. Фонд оценочных средств для проведения промежуточной аттестации по
модулю (Приложение 1)
5
6.
ПРИЛОЖЕНИЕ 1к рабочей программе модуля
5.3. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ПРОМЕЖУТОЧНОЙ
АТТЕСТАЦИИ ПО МОДУЛЮ
5.3.1. ОБЩИЕ КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО МОДУЛЮ
Система критериев оценивания результатов обучения в рамках модуля опирается на
три уровня освоения: пороговый, повышенный, высокий.
Компоненты
Признаки уровня освоения компонентов компетенций
компетенций
пороговый
повышенный
высокий
Студент демонстрирует
Студент демонстрирует Студент может
Знания
знание-знакомство,
аналитические знания:
самостоятельно
знание-копию: узнает
уверенно воспроизводит извлекать новые знания
объекты, явления и
и понимает полученные из окружающего мира,
понятия, находит в них
знания, относит их к той творчески их
различия, проявляет
или иной
использовать для
знание источников
классификационной
принятия решений в
получения информации,
группе, самостоятельно новых и нестандартных
может осуществлять
систематизирует их,
ситуациях.
самостоятельно
устанавливает
репродуктивные действия взаимосвязи между
над знаниями путем
ними, продуктивно
самостоятельного
применяет в знакомых
воспроизведения и
ситуациях.
применения информации.
Студент умеет корректно
Студент умеет
Студент умеет
Умения
выполнять предписанные самостоятельно
самостоятельно
действия по инструкции,
выполнять действия
выполнять действия,
алгоритму в известной
(приемы, операции) по
связанные с решением
ситуации, самостоятельно решению нестандартных исследовательских
выполняет действия по
задач, требующих
задач, демонстрирует
решению типовых задач,
выбора на основе
творческое
требующих выбора из
комбинации известных использование умений
числа известных методов, методов, в
(технологий)
в предсказуемо
непредсказуемо
изменяющейся ситуации
изменяющейся ситуации
Студент имеет
Студент имеет
Личностные Студент имеет низкую
мотивацию учебной
выраженную мотивацию развитую мотивацию
качества
деятельности, проявляет
учебной деятельности,
учебной и трудовой
безразличное,
демонстрирует
деятельности,
безответственное
позитивное отношение к проявляет
отношение к учебе,
обучению и будущей
настойчивость и
порученному делу
трудовой деятельности, увлеченность,
проявляет активность.
трудолюбие,
самостоятельность,
творческий подход.
5.3.2. ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ПРОВЕДЕНИЯ ПРОМЕЖУТОЧНОЙ
6
7.
АТТЕСТАЦИИ ПО МОДУЛЮ5.3.2.1. Перечень примерных вопросов для интегрированного экзамена по
модулю.
Не предусмотрено
5.3.2.2. Перечень примерных тем итоговых проектов по модулю.
Не предусмотрено
7
8.
6. ЛИСТ РЕГИСТРАЦИИ ИЗМЕНЕНИЙ В РАБОЧЕЙ ПРОГРАММЕ МОДУЛЯНомер листа
изменений
Номер
Дата
протокола
заседания
Всего листов в
заседания
проектной
документе
проектной
группы модуля
группы модуля
8
Подпись
руководителя
проектной группы
модуля
9.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное автономное образовательное учреждение
высшего образования
«Уральский федеральный университет имени первого Президента России Б.Н. Ельцина»
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ
Перечень сведений о рабочей программе
дисциплины
Модуль
Специальные главы математики
Образовательная программа
Прикладная математика
Направление подготовки
Прикладная математика
Уровень подготовки
Бакалавриат
ФГОС ВО
Учетные данные
Код модуля 1127561
Учебный план в ЕИСУ № 6104
Код ОП
01.03.04/01.01
Код направления и уровня подготовки
01.03.04
Реквизиты приказа Минобрнауки РФ об
утверждении ФГОС ВО:
12 марта 2015 г., № 208
Екатеринбург, 2017
9
10.
Рабочая программа дисциплины составлена авторами:№ п/п
ФИО
1
Гредасова
Надежда Викторовна
Полищук
Ефим Григорьевич
2
Ученая степень,
ученое звание
Канд. физ.-мат.
наук
Канд. физ.-мат.
наук, доцент
Руководитель модуля
Должность
Доцент
Доцент
Кафедра
Подпись
Прикладная
математика
Прикладная
математика
А.Н. Сесекин
Рекомендовано учебно-методическим советом Уральского энергетического института
Председатель учебно-методического совета
Протокол № ______ от __________ г.
Е.В. Черепанова
Согласовано:
Дирекция образовательных программ
Р.Х. Токарева
10
11.
1. ОБЩАЯ ХАРАКТЕРИСТИКА ДИСЦИПЛИНЫ ФУНКЦИОНАЛЬНЫЙАНАЛИЗ
1.1.Аннотация содержания дисциплины
Дисциплина относится к модулю «Специальные главы математики» (базовая часть).
Дисциплины модуля: Теория функций комплексного переменного (3 семестр), Обыкновенные
дифференциальные уравнения и теория устойчивости (3, 4 семестры), Дискретная математика
(3,4 семестры), Теория вероятностей и математическая статистика (4 семестр), Введение в
специальность (3 семестр).
Дисциплина посвящена изучению основ теории множеств, метрических пространств,
теории меры, измеримых функций и интеграла, теории нормированных пространств,
линейных функционалов и операторов.
1.2. Язык реализации программы – русский
1.3. Планируемые результаты обучения по дисциплине
Результатом обучения в рамках дисциплины является формирование у студента
следующих компетенций:
ОПК-1 - готовность к самостоятельной работе;
ПК-9 - способность выявить естественнонаучную сущность проблем,
возникающих в ходе профессиональной деятельности, готовностью
использовать для их решения соответствующий естественнонаучный аппарат;
ПК-10 - готовность применять математический аппарат для решения
поставленных задач, способностью применить соответствующую процессу
математическую модель и проверить ее адекватность, провести анализ
результатов моделирования, принять решение на основе полученных
результатов;
ПК-12 - способность самостоятельно изучать новые разделы
фундаментальных наук;
В результате освоения дисциплины студент должен:
Знать:
- основные понятия метрических, нормированных и гильбертовых пространств;
- понятия меры и измеримых функций.
Уметь:
доказывать теоремы функционального анализа.
Владеть (демонстрировать навыки и опыт деятельности):
методами функционального анализа.
1.4.Объем дисциплины
Очная форма обучения
Объем дисциплины
№
п/
п
1.
2.
3.
Виды учебной работы
Распределение объема
дисциплины по
семестрам (час.)
Всего часов
В т.ч.
контактная
работа (час.)*
4
51
34
17
51
34
17
51
34
17
Аудиторные занятия
Лекции
Практические занятия
11
12.
4.5.
6.
7.
8.
Лабораторные работы
Самостоятельная работа студентов,
включая все виды текущей
аттестации
Промежуточная аттестация
Общий объем по учебному плану,
час.
Общий объем по учебному плану,
з.е.
53
7,65
53
18
0,25
З (4)
108
58,90
108
3
3
*Контактная работа составляет:
в п/п 2,3,4 - количество часов, равное объему соответствующего вида занятий;
в п.5 – количество часов, равное сумме объема времени, выделенного преподавателю на консультации в
группе (15% от объема аудиторных занятий) и объема времени, выделенного преподавателю на руководство
курсовой работой/проектом одного студента, если она предусмотрена.
в п.6 – количество часов, равное сумме объема времени, выделенного преподавателю на проведение
соответствующего вида промежуточной аттестации одного студента и объема времени, выделенного в рамках
дисциплины на руководство проектом по модулю (если он предусмотрен) одного студента.
2. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
Код
раздела,
темы
P1
P2
P3
P4
P5
Раздел, тема
дисциплины
Содержание
Теоретико-множественные операции. Отношения
эквивалентности. Разбиения на классы.
Открытые и замкнутые множества, их объединения,
пересечения и дополнения. Свойства операции
замыкания. Полнота и теорема о вложенных шарах.
Теорема Бэра. Компактность и теорема
Метрические пространства
Вейерштрасса. Принцип сжатых отображений и его
применения к построению процедур приближенного
решения уравнений в конечномерных и
бесконечномерных пространствах.
Счетно аддитивные меры. Продолжение меры по
Лебегу. Эквивалентные определения измеримых
функций. Свойства измеримых функций.
Измеримость точной верхней и нижней грани, а
также поточечного верхнего и нижнего пределов
Мера, измеримые функции последовательности измеримых функций.
и интеграл
Соотношение между равномерной сходимостью,
сходимостью почти всюду, сходимостью по мере.
Интеграл Лебега и его свойства. Сигма –
аддитивность интеграла. Предельный переход под
знаком интеграла( теоремы Лебега, Леви, Фату).
Связь интеграла Римана и Лебега.
Неравенства Буняковского и Коши. Соотношения
между сходимостями в среднем квадратичном, по
мере и слабой сходимостью. Неравенство Бесселя.
Гильбертово пространство Теорема Рисса-Фишера. Критерий замкнутости
ортонормированной системы. Ортогонализация
Шмидта.
Теория множеств
Нормированные
пространства
Линейное нормированное пространство. Линейный
непрерывный функционал и его норма. Общий вид
12
13.
линейного функционала в конкретныхфункциональных пространствах. Полнота
сопряженного пространства. Слабая сходимость.
Слабая компактность шара в сопряженном
пространстве. Линейные непрерывные операторы.
Теоремы об обратном операторе.
3. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ
3.1. Распределение аудиторной нагрузки и мероприятий самостоятельной работы по
разделам дисциплины
13
14.
Объем модуля (зач.ед.):28Объем дисциплины (зач.ед.):3
Очная форма обучения Учебный план № 6104
Аудиторные
занятия (час.)
14
8
4
4
6
1
26
12
8
4
14
8
4
4
6
1
22
12
8
4
10
8
4
4
20
17
Всего (час), без учета
104
51
34
17
53
37
промежуточной
аттестации:
Всего по дисциплине
108
51
57
(час.):
*Суммарный объем в часах на мероприятие
указывается в строке «Всего (час.) без учета промежуточной аттестации
12
12
2
1
4
4
В т.ч. промежуточная аттестация
14
Проект по модулю
4
Интегрированный экзамен по модулю
6
Экзамен
10
1
Подгото
вка в
рамках
дисципл
ины к
промежу
точной
аттестац
ии по
модулю
(час.)
Зачет
24
2
Подготов
ка к
промежут
очной
аттестац
ии по
дисципли
не (час.)
Коллоквиум*
3
Контрольная работа*
4
Подготовка к
контрольным
мероприятиям
текущей
аттестации
(колич.)
Всего (час.)
7
Курсовой проект*
9
Курсовая работа*
3
Перевод инояз. литературы*
6
Домашняя работа на иностр.
языке*
9
Расчетно-графическая работа*
18
Расчетная работа, разработка
программного продукта*
2
Проектная работа*
4
Реферат, эссе, творч. работа*
6
Домашняя работа*
6
Всего (час.)
2
Н/и семинар, семинар-конфер.,
коллоквиум (магистратура)
6
Лабораторное занятие
8
Графическая работа*
Всего самостоятельной работы студентов (час.)
14
Лабораторные работы
Практ., семинар. занятие
Нормированные
пространства
Лекция
Гильбертово пространство
Всего (час.)
Мера, измеримые функции
и интеграл
Практические занятия
Метрические пространства
Выполнение самостоятельных внеаудиторных работ (колич.)
Лекции
P
5
Теория множеств
Подготовка к аудиторным
занятиям (час.)
Всего аудиторной работы (час.)
P
1
P
2
P
3
P
4
Наименование раздела,
темы
Самостоятельная работа: виды, количество и объемы мероприятий
Всего по разделу, теме (час.)
Код раздела, темы
Раздел дисциплины
4
0
0
0
15.
4. ОРГАНИЗАЦИЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ, САМОСТОЯТЕЛЬНОЙ РАБОТЫПО ДИСЦИПЛИНЕ
6.1. Лабораторные работы
Не предусмотрены
Код
раздела,
темы
6.2. Практические занятия
Номер
занятия
Тема занятия
Время на
проведение
занятия (час.)
Р1
Р2
Р3
Р4
Р5
1
2
3
4
5
Теория множеств
Метрические пространства
Мера, измеримые функции и интеграл
Гильбертово пространство
Нормированные пространства
2
3
4
4
4
Всего:
3. 4.3.Примерная тематика самостоятельной работы
4.3.1. Примерный перечень тем домашних работ
Мера, измеримые функции и интеграл.
Гильбертово пространство.
4.3.2. Примерный перечень тем графических работ
Не предусмотрено
4.3.3. Примерный перечень тем рефератов (эссе, творческих работ)
Не предусмотрено
4.3.4 Примерная тематика индивидуальных или групповых проектов
Не предусмотрено
4.3.5. Примерный перечень тем расчетных работ (программных продуктов)
Не предусмотрено
4.3.6. Примерный перечень тем расчетно-графических работ
Не предусмотрено
4.3.7. Примерный перечень тем курсовых проектов (курсовых работ)
Не предусмотрено
4.4.1. Примерная тематика контрольных работ
Метрические пространства.
Нормированные пространства.
4.3.9. Примерная тематика коллоквиумов
Не предусмотрено
15
17
16.
5. СООТНОШЕНИЕ РАЗДЕЛОВ, ТЕМ ДИСЦИПЛИНЫ И ПРИМЕНЯЕМЫХТЕХНОЛОГИЙ ОБУЧЕНИЯ
Р1-Р5
Другие (указать, какие)
Вебинары и
видеоконференции
Асинхронные webконференции и семинары
Совместная работа и
разработка контента
Виртуальные практикумы
и тренажеры
Дистанционные
образовательные технологии и
электронное обучение
Сетевые учебные курсы
Другие (указать, какие)
Командная работа
Проблемное обучение
Деловые игры
Кейс-анализ
Код раздела, темы
дисциплины
Проектная работа
Активные методы обучения
*
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ
(Приложение 1)
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХ
НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ (Приложение 2)
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ (Приложение 3)
9. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ
ДИСЦИПЛИНЫ
9.1.Рекомендуемая литература
9.1.1.Основная литература
1. Треногин, В. А. Функциональный анализ / В.А. Треногин .— 3-е изд., испр. — Москва :
Физматлит,
2002
.—
488
с.
—
ISBN
5-9221-0272-9
.—
<URL:http://biblioclub.ru/index.php?page=book&id=82613>. (ЭБС
2. Колмогоров, А. Н. Элементы теории функций и функционального анализа / А.Н.
Колмогоров ; С.В. Фомин .— 7-е изд. — Москва : Физматлит, 2012 .— 573 с. — (Классический
университетский
учебник)
.—
ISBN
978-5-9221-0266-7
.—
<URL:http://biblioclub.ru/index.php?page=book&id=82563>.
3. Князев, Павел Николаевич. Функциональный анализ : Учеб. пособие для студентов мат.
специальностей вузов / П. Н. Князев .— 2-е изд., стер. — М. : Эдиториал УРСС, 2003 .— 208 с.
— Библиогр.: с. 204. — ISBN 5-354-00430-6 : 129.00.
9.1.2.Дополнительная литература
1. Лебедев, В. И. Функциональный анализ и вычислительная математика / В.И. Лебедев .— 4е изд., перераб. и доп. — Москва : Физматлит, 2005 .— 294 с. — ISBN 5-9221-0092-0 .—
<URL:http://biblioclub.ru/index.php?page=book&id=68363>.
2. Люстерник, Лазарь Аронович. Элементы функционального анализа / Л. А. Люстерник, В.
И. Соболев .— Изд. 2-е, перераб. — Москва : Наука, 1965 .— 520 с. : ил. ; 21 см .— Предм.
указ.: с. 514-519. — Библиогр.: с. 512-513 (35 назв.).
9.2.Методические разработки
16
17.
Не используются9.3.Программное обеспечение
Не используется
9.4. Базы данных, информационно-справочные и поисковые системы
http://study.urfu.ru – портал информационно-образовательных ресурсов УрФУ
http://lib.urfu.ru – зональная научная библиотека УрФУ
http://poiskknig.ru – электронная библиотека учебников Мех-Мата МГУ, Москва
http://www.mathnet.ru. - общероссийский математический портал
http://onlinelibrary.wiley.com - научные журналы издательства Wiley&Sons
http://www.sciencedirect.com - научные журналы издательства Elsevier
https://www.coursera.org/ – массовые открытые онлайн-курсы;
https://www.edx.org/ – массовые открытые онлайн-курсы;
https://openedu.ru/ – национальная платформа открытого образования;
9.5.Электронные образовательные ресурсы
Не используются
10. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Сведения об оснащенности дисциплины специализированным и лабораторным
оборудованием
Мультимедийная аудитория Т-1208: 10 ПК, проектор; мультимедийная аудитория Т1202б: 10 ПК, проектор, интерактивная доска.
17
18.
ПРИЛОЖЕНИЕ 1к рабочей программе дисциплины
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В
РАМКАХ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
6.1. Весовой коэффициент значимости дисциплины –
6.2.Процедуры текущей и промежуточной аттестации по дисциплине
1.Лекции: коэффициент значимости совокупных результатов лекционных занятий – 0,6
Текущая аттестация на лекциях
Сроки –
Максималь
семестр,
ная оценка
учебная
в баллах
неделя
Экспертиза конспекта
6, 1-17
100
Весовой коэффициент значимости результатов текущей аттестации по лекциям – 0.4
Промежуточная аттестация по лекциям – экзамен
Весовой коэффициент значимости результатов промежуточной аттестации по лекциям –
0,6
2. Практические/семинарские занятия: коэффициент значимости совокупных
результатов практических/семинарских занятий – 0,4
Текущая аттестация на практических/семинарских
Сроки –
Максималь
занятиях
семестр,
ная оценка
учебная
в баллах
неделя
Контрольная работа № 1
6,12
20
Контрольная работа № 2
6,15
20
Домашняя работа № 1
6,14
16
Домашняя работа № 2
6,17
16
Работа на практических занятиях
6,9-17
28
Весовой коэффициент значимости результатов текущей аттестации по
практическим/семинарским занятиям – 1
Промежуточная аттестация по практическим/семинарским занятиям – нет
Весовой коэффициент значимости результатов промежуточной аттестации по
практическим/семинарским занятиям – 0
3. Лабораторные занятия: коэффициент значимости совокупных результатов
лабораторных занятий – не предусмотрено
6.3. Процедуры текущей и промежуточной аттестации курсовой работы/проекта
6.4. Коэффициент значимости семестровых результатов освоения дисциплины
Порядковый номер семестра по учебному
Коэффициент значимости результатов
плану, в котором осваивается дисциплина
освоения дисциплины в семестре
1
Семестр
*В случае проведения промежуточной аттестации по дисциплине (экзамена, зачета) методом
тестирования используются официально утвержденные ресурсы: АПИМ УрФУ, СКУД УрФУ,
имеющие статус ЭОР УрФУ; ФЭПО (www.фэпо.рф); Интернет-тренажеры (www.i-exam.ru).
18
19.
ПРИЛОЖЕНИЕ 2к рабочей программе дисциплины
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХ
НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
сайте ФЭПО http://fepo.i-exam.ru.
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
сайте Интернет-тренажеры http://training.i-exam.ru.
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
портале СМУДС УрФУ.
В связи с отсутствием Дисциплины и ее аналогов, по которым возможно
тестирование, на сайтах ФЭПО, Интернет-тренажеры и портале СМУДС УрФУ,
тестирование в рамках НТК не проводится.
19
20.
ПРИЛОЖЕНИЕ 3к рабочей программе дисциплины
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
8.1. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ КОНТРОЛЬНО-ОЦЕНОЧНЫХ
МЕРОПРИЯТИЙ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО
ДИСЦИПЛИНЕ В РАМКАХ БРС
В рамках БРС применяются утвержденные на кафедре критерии оценивания
достижений студентов по каждому контрольно-оценочному мероприятию. Система критериев
оценивания, как и при проведении промежуточной аттестации по модулю, опирается на три
уровня освоения компонентов компетенций: пороговый, повышенный, высокий.
Компоненты
Признаки уровня освоения компонентов компетенций
компетенций
пороговый
повышенный
высокий
Студент демонстрирует
Студент демонстрирует Студент может
Знания
знание-знакомство,
аналитические знания:
самостоятельно
знание-копию: узнает
уверенно воспроизводит извлекать новые знания
объекты, явления и
и понимает полученные из окружающего мира,
понятия, находит в них
знания, относит их к той творчески их
различия, проявляет
или иной
использовать для
знание источников
классификационной
принятия решений в
получения информации,
группе, самостоятельно новых и нестандартных
может осуществлять
систематизирует их,
ситуациях.
самостоятельно
устанавливает
репродуктивные действия взаимосвязи между
над знаниями путем
ними, продуктивно
самостоятельного
применяет в знакомых
воспроизведения и
ситуациях.
применения информации.
Студент умеет корректно
Студент умеет
Студент умеет
Умения
выполнять предписанные самостоятельно
самостоятельно
действия по инструкции,
выполнять действия
выполнять действия,
алгоритму в известной
(приемы, операции) по
связанные с решением
ситуации, самостоятельно решению нестандартных исследовательских
выполняет действия по
задач, требующих
задач, демонстрирует
решению типовых задач,
выбора на основе
творческое
требующих выбора из
комбинации известных использование умений
числа известных методов, методов, в
(технологий)
в предсказуемо
непредсказуемо
изменяющейся ситуации
изменяющейся ситуации
Студент имеет
Студент имеет
Личностные Студент имеет низкую
мотивацию учебной
выраженную мотивацию развитую мотивацию
качества
деятельности, проявляет
учебной деятельности,
учебной и трудовой
безразличное,
демонстрирует
деятельности,
безответственное
позитивное отношение к проявляет
отношение к учебе,
обучению и будущей
настойчивость и
порученному делу
трудовой деятельности, увлеченность,
проявляет активность.
трудолюбие,
самостоятельность,
творческий подход.
20
21.
8.2. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИПРИ ИСПОЛЬЗОВАНИИ НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ
При проведении независимого тестового контроля как формы промежуточной
аттестации применяется методика оценивания результатов, предлагаемая разработчиками
тестов. Процентные показатели результатов независимого тестового контроля переводятся в
баллы промежуточной аттестации по 100-балльной шкале в БРС:
в случае балльной оценки по тесту (блокам, частям теста) переводится процент набранных
баллов от общего числа возможных баллов по тесту;
при отсутствии балльной оценки по тесту переводится процент верно выполненных
заданий теста, от общего числа заданий.
8.3. ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ
И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
8.3.1. Примерные задания для проведения домашней работы
Домашняя работа № 1
1. Пусть f n (x) – последовательность измеримых функций. Доказать, что функции sup f n (x) и
inf f n (x) – измеримы.
2. Положим для функции f: f (x) = ( f(x) + |f(x)| )/2, f (x) = ( f(x) - |f(x)| )/2. Доказать, что
функция f суммируема т. и т.т., когда f и f суммируемы.
Домашняя работа № 2
1. Доказать, что всякая ортонормированная последовательность в гильбертовом
пространстве сходится слабо, но не сильно.
2. Пусть последовательность {x n } элементов гильбертого пространства слабо сходится к
элементу x, причем ||x n || ||x|| при n . Доказать, что x n x сильно.
8.3.2. Примерные контрольные задачи в рамках учебных занятий
Контрольная работа № 1
3. Доказать, что в метрическом пространстве последовательность не может иметь два
предела.
4. Доказать, что подпространство в полном метрическом пространстве X полно т. и т.т.,
когда оно замкнуто в X.
Контрольная работа № 2
3. Пусть в линейном пространстве заданы две нормы ||x|| 1 и ||x|| 2 . Доказать, что ||x|| = ||x|| 1 +
||x|| 2 есть тоже норма.
4. Пусть в линейном пространстве заданы две нормы ||x|| 1 и ||x|| 2 . Доказать, что ||x|| =
max(||x|| 1 ,||x|| 2 ) есть тоже норма.
5. Доказать, что единичный шар в нормированном пространстве есть выпуклое множество.
8.3.3. Примерные контрольные кейсы
Не предусмотрено
8.3.4. Перечень примерных вопросов для зачета
1. Понятие метрического пространства. Определение и примеры. Неравенства Гельдера,
Минковского. Предельные точки. Сходимость. Плотные множества. Открытые и
замкнутые множества. Непрерывные отображения метрических пространств.
2. Полные метрические пространства. Определения и примеры полных метрических
пространств. Теорема о вложенных шарах. Теорема Бэра.
3. Принцип сжимающих отображений. Простейшие применения принципа сжимающих
отображений.
21
22.
4. Компактность в метрических пространствах. Полная ограниченность. Компактность иполная ограниченность. Предкомпактные подмножества в метрических пространствах.
Теорема Арцела. Непрерывные отображения метрических компактов.
5. Мера плоских множеств.Мера элементарных множеств. Лебегово продолжение меры.
Лебегова мера плоских множеств.
6. Измеримые функции. Определение и основные свойства измеримых функций.
Действия над измеримыми функциями. Эквивалентность. Сходимость почти
всюду. Сходимость по мере.
7. Интеграл Лебега. Простые функции. Интеграл Лебега для простых функций. Общее
определение интеграла Лебега на множестве конечной меры. Сигма-аддитивность и
абсолютная непрерывность интеграла Лебега. Предельный переход под знаком
интеграла Лебега. Интеграл Лебега по множеству бесконечной меры.
8. Сравнение с интегралом Римана.
9. Понятие линейного пространства. Норма. Единичный шар.
10. Евклидовы пространства. Неравенство Коши-Буняковского. Понятие
ортонормированного базиса. Процесс ортогонализации. Неравенство Бесселя.
Равенство Парсеваля. Теорема об эквивалентности в сепарабельном пространстве
полноты и замкнутости ортонормированной системы. Теорема Рисса-Фишера.
11. Гильбертовы пространства. Изоморфизм.
12. Характеристическое свойство евклидовых пространств.
13. Линейные функционалы в нормированных пространства. Непрерывность и
ограниченность линейного функционала. Норма линейного функционала. Теорема
Хана-Банаха (формулировка).
14. Сопряженное пространство. Его полнота.
15. Слабо сходящиеся последовательности. Их ограниченность. Достаточные условия для
слабой сходимости.
8.3.5. Перечень примерных вопросов для экзамена
Не предусмотрено
8.3.6. Ресурсы АПИМ УрФУ, СКУД УрФУ для проведения тестового контроля в рамках
текущей и промежуточной аттестации
Не используются
8.3.7. Ресурсы ФЭПО для проведения независимого тестового контроля
Не используются
8.3.8. Интернет-тренажеры
Не используются
22
23.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное автономное образовательное учреждение
высшего образования
«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ТЕОРИЯ УСТОЙЧИВОСТИ
Перечень сведений о рабочей программе
дисциплины
Модуль Специальные главы математики
Учетные данные
Код модуля 1127561
Учебный план в ЕИСУ № 6104
Код ОП
01.03.04/01.01
Код направления и уровня
подготовки.
01.03.04
Образовательная программа
Прикладная математика
Направление подготовки
Прикладная математика
Уровень подготовки
Бакалавриат
ФГОС ВО
Реквизиты приказа Минобрнауки
РФ об утверждении ФГОС ВО:
12 марта 2015 г., № 208
Екатеринбург, 2017
23
24.
Рабочая программа дисциплины составлена авторами:№ п/п
ФИО
1
Сесекин Александр
Николаевич
Ученая степень,
ученое звание
Д.ф.-м.н.,
профессор
Руководитель модуля
Должность
Профессор
Кафедра
Подпись
Прикладн
ая
математи
ка
А.Н. Сесекин
Рекомендовано учебно-методическим советом Уральского энергетического института
Председатель учебно-методического совета
Протокол № ______ от __________ г.
Е.В. Черепанова
Согласовано:
Дирекция образовательных программ
Р.Х. Токарева
24
25.
2. ОБЩАЯ ХАРАКТЕРИСТИКА ДИСЦИПЛИНЫ «Обыкновенныедифференциальные уравнения и теория устойчивости»
1.2.Аннотация содержания дисциплины
Дисциплина относится к модулю «Специальные главы математики» (базовая часть).
Дисциплины модуля: Теория функций комплексного переменного и операционное исчисление
(3 семестр), Функциональный анализ (4 семестр), Дискретная математика (3,4 семестры),
Теория вероятностей и математическая статистика (4 семестр), Введение в специальность (3
семестр).
Дифференциальные уравнения являются мощным средством для описания и
математического моделирования реальных процессов в механике, физике и других областях
знания. Курс «Обыкновенные дифференциальные уравнения и теория устойчивости»
посвящен методам интегрирования обыкновенных дифференциальных уравнений, элементам
качественной теории дифференциальных уравнений и теории устойчивости. Эта дисциплина
входит в модуль «Специальные главы математики»
1.2. Язык реализации программы – русский.
1.3. Планируемые результаты обучения по дисциплине
Результатом обучения в рамках дисциплины является формирование у студента
следующих компетенций:
ОПК1. Готовностью к самостоятельной работе (ОПК-1).
ОПК2. Способностью использовать современные математические методы и современные
прикладные программные средства и осваивать современные технологии программирования
(ОПК-2).
ПК9. Способностью выявить естественнонаучную сущность проблем, возникающих в ходе
профессиональной деятельности, готовностью использовать для их решения соответствующий
естественнонаучный аппарат (ПК-9).
ПК10. Готовностью применять математический аппарат для решения поставленных задач,
способностью применить соответствующую процессу математическую модель и проверить ее
адекватность (ПК-10).
ПК12. Способностью самостоятельно изучать новые разделы фундаментальных наук (ПК-12).
В результате освоения дисциплины студент должен:
Знать:
основные типы дифференциальных уравнений первого порядка и дифференциальных
уравнений высших порядков и систем дифференциальных уравнений, методы их
интегрирования;
базовые понятия качественной теории дифференциальных уравнений;
основные понятия и методы теории устойчивости.
Уметь:
применять методы интегрирования основных типов дифференциальных уравнений и
систем;
составлять дифференциальные уравнения для описания простейших физических
явлений;
применять теоремы качественной теории дифференциальных уравнений к конкретным
типам дифференциальных уравнений.
исследовать на устойчивость решения линейных и нелинейных систем
дифференциальных уравнений.
Владеть (демонстрировать навыки и опыт деятельности):
25
26.
навыками построения простейших математических моделей технических иэкономических систем;
навыками исследовать динамические модели на устойчивость;
навыками интегрирования уравнений динамических моделей.
5.4.Объем дисциплины
Объем дисциплины
№
п/
п
Виды учебной работы
1.
2.
3.
4.
5.
6.
7.
8.
Распределение объема
дисциплины по семестрам (час.)
Всего
часов
В т.ч.
контактн
ая работа
(час.)*
3
4
Аудиторные занятия
Лекции
Практические занятия
Лабораторные работы
Самостоятельная работа студентов,
включая все виды текущей
аттестации
Промежуточная аттестация
102
51
51
102
51
51
68
34
34
34
17
17
92
15,3
58
34
22
2,58
Общий объем по учебному плану,
час.
Общий объем по учебному плану,
з.е.
216
119,88
Э, 18
144
З, 4
72
4
2
6
*Контактная работа составляет:
в п/п 2,3,4 - количество часов, равное объему соответствующего вида занятий;
в п.5 – количество часов, равное сумме объема времени, выделенного преподавателю на консультации в
группе (15% от объема аудиторных занятий) и объема времени, выделенного преподавателю на руководство
курсовой работой/проектом одного студента, если она предусмотрена.
в п.6 – количество часов, равное сумме объема времени, выделенного преподавателю на проведение
соответствующего вида промежуточной аттестации одного студента и объема времени, выделенного в рамках
дисциплины на руководство проектом по модулю (если он предусмотрен) одного студента.
6. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
Код
раздела,
темы
Р1
Р2
Раздел, тема
дисциплины*
Содержание
Дифференциальные
Задачи,
приводимые
к
дифференциальным
уравнения первого порядка уравнениям. Основные понятия: первый интеграл,
общий интеграл, задача Коши. Поле направлений.
Дифференциальные уравнения с разделяющимися
переменными.
Однородные
дифференциальные
уравнения. Линейные дифференциальныe ypавнeния
(метод Бернулли, метод вариации произвольных
постоянных).
Уравнение
Бернулли.
Дифференциальное
уравнение
в
полных
дифференциалах. Интегрирующий множитель.
Общая теория
Теорема существования и единственности решения
дифференциальных
дифференциального уравнения. Продолжимость
26
27.
уравненийР3
Р4
Р5
Р6
Р7
Р8
решений
дифференциальных
уравнений.
Непрерывная
зависимость
решений
дифференциальных уравнений от начальных условий
и параметров.
Дифференциальные
Уравнения, не разрешенные относительно
уравнения, не
производной. Общий метод введения параметра.
разрешенные относительно Уравнения Лагранжа и Клеро. Особые решения.
производной
Огибающая семейства кривых.
Задачи маршрутизации перемещений, где
рассматривается задача коммивояжера и ее
Дифференциальные
обобщения, связанные с заменой городов
уравнения высших порядков
мегаполисами и введением так называемых условий
предшествования, для которых обсуждаются как
точные, так и приближенные методы решения.
Теорема существования и единственности решения
дифференциального уравнения n-го порядка (без
доказательства). Понижение порядка
дифференциального уравнения. Определитель
Вронского. Критерий линейной зависимости системы
функций. Критерий линейной независимости
решений линейного однородного
дифференциального уравнения n-го порядка.
Структура общего решения линейного однородного
дифференциального уравнения n-го порядка.
Системы дифференциальных
Структура общего решения линейного
уравнений
неоднородного дифференциального уравнения n-го
порядка. Построение общего решения линейного
однородного дифференциального уравнения n-го
порядка с постоянными коэффициентами. Метод
вариации произвольных постоянных. Уравнение
Эйлера. Методы нахождения частных решений
неоднородных линейных дифференциальных
уравнений n-го порядка с постоянными
коэффициентами. Краевые задачи для
дифференциальных уравнений высоких порядков.
Классификация точек покоя линейных однородных
Фазовые портреты особых
точек
систем второго порядка
Задачи, приводимые к понятию устойчивости
движения. Определения устойчивости,
асимптотической устойчивости и неустойчивости по
Основные понятия теории
Ляпунову. Другие определения устойчивости.
устойчивости. Метод
Теоремы Ляпунова об устойчивости,
функций Ляпунова
асимптотической устойчивости и неустойчивости.
Геометрический смысл метода функций Ляпунова.
Теорема Барбашина-Красовского.
Общие теоремы об устойчивости линейных
дифференциальных систем. Устойчивость линейных
однородных дифференциальных систем.
Устойчивость линейной дифференциальной системы
Исследование устойчивости
линейных и нелинейных
с постоянными коэффициентами. Критерий Гурвица.
систем
Способы построения функций Ляпунова для
линейных систем с постоянными коэффициентами.
Лемма Гронуолла. Устойчивость нелинейных систем
по первому приближению. Построение фазовых
27
28.
портретов нелинейных систем второго порядка7. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ
3.2. Распределение аудиторной нагрузки и мероприятий самостоятельной работы по
разделам дисциплины
28
29.
Объем модуля 28 (зач.ед.):Объем дисциплины 6 (зач.ед.):
Аудиторные
занятия (час.)
Подготовка к
контрольным
мероприятиям
текущей аттестации
(колич.)
16
8
4
4
8
6
2
4
26
12
6
6
14
8
4
4
26
16
6
6
10
8
4
Р
6
Фазовые портреты особых точек
16
8
4
4
8
6
Основные понятия теории
устойчивости. Метод функций
Ляпунова
Исследование устойчивости
линейных и нелинейных систем
28
16
8
8
12
24
10
5
5
14
Р
3
Р
4
Р
7
Р
8
Всего (час), без учета
102
194
51
51 0
92
промежуточной аттестации:
Всего по дисциплине (час.):
216
0
114
*Суммарный объем в часах на мероприятие
указывается в строке «Всего (час.) без учета промежуточной аттестации
2
4
2
1
10
4
6
2
1
8
4
4
66
28
38
8
4
0
0
Курсовой проект*
1
Курсовая работа*
2
6
Проектная работа*
4
Домашняя работа*
1
Всего (час.)
2
Проект по модулю
4
Интегрированный экзамен по модулю
2
Экзамен
6
1
4
18
0
0
1
6
1
2918
3
0
0
0
0
0
0
0
0
Подгот
овка в
рамках
дисцип
лины к
проме
жуточн
ой
аттест
ации
по
модул
ю
(час.)
Зачет
6
6
Подготов
ка к
промежут
очной
аттестац
ии по
дисципли
не (час.)
Коллоквиум*
4
Контрольная работа*
6
Всего (час.)
10
Перевод инояз. литературы*
16
Р
2
Домашняя работа на иностр.
языке*
8
Расчетно-графическая работа*
6
Расчетная работа, разработка
программного продукта*
14
Реферат, эссе, творч. работа*
20
Графическая работа*
Практ., семинар. занятие
12
Лабораторное занятие
Лекция
10
Выполнение самостоятельных внеаудиторных работ
(колич.)
Н/и семинар, семинар-конфер.,
коллоквиум (магистратура)
Всего (час.)
22
Р
1
Наименование раздела, темы
Лабораторные работы
Практические занятия
42
Р
5
Дифференциальные уравнения
первого порядка
Общая теория
дифференциальных уравнений
Дифференциальные уравнения,
не разрешенные относительно
производной
Дифференциальные уравнения
высших порядков
Системы дифференциальных
уравнений
Код раздела, темы
Лекции
Подготовка к
аудиторным занятиям
(час.)
Всего аудиторной работы (час.)
Всего самостоятельной работы студентов (час.)
Самостоятельная работа: виды, количество и объемы мероприятий
Всего по разделу, теме (час.)
Раздел дисциплины
0
В т.ч. промежуточная аттестация
30.
3031.
8. ОРГАНИЗАЦИЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ, САМОСТОЯТЕЛЬНОЙ РАБОТЫПО ДИСЦИПЛИНЕ
6.3. Лабораторные работы
Не предусмотрено
Код
раздела,
темы
6.4. Практические занятия
Р1
Р2
Р3
Р4
Р5
Р6
Р7
Номер
занятия
1
2
3
4
5
6
7
Тема занятия
Дифференциальные уравнения первого порядка
Общая теория дифференциальных уравнений
Дифференциальные уравнения, не разрешенные
относительно производной
Дифференциальные уравнения высших порядков
Системы дифференциальных уравнений
Фазовые портреты особых точек
Основные понятия теории устойчивости. Метод
функций Ляпунова
Всего:
Время на
проведение
занятия (час.)
12
4
4
6
6
4
8
51
4. 4.3.Примерная тематика самостоятельной работы
4.3.4. Примерный перечень тем домашних работ
1. Дифференциальные уравнения первого порядка.
2. Дифференциальные уравнения высших порядков.
3. Исследование устойчивости линейных и нелинейных систем.
4.3.5. Примерный перечень тем графических работ
Не предусмотрено.
4.3.6. Примерный перечень тем рефератов (эссе, творческих работ)
Не предусмотрено.
4.3.4 Примерная тематика индивидуальных или групповых проектов
Не предусмотрено.
4.3.8. Примерный перечень тем расчетных работ (программных продуктов)
Не предусмотрено.
4.3.9. Примерный перечень тем расчетно-графических работ
Не предусмотрено.
4.3.10. Примерный перечень тем курсовых проектов (курсовых работ)
Не предусмотрено.
4.3.11. Примерная тематика контрольных работ
1. Дифференциальные уравнения, не разрешенные относительно производной.
2. Линейные системы дифференциальных уравнений.
3. Фазовые портреты особых точек.
4. Основные понятия теории устойчивости. Метод функций Ляпунова.
4.3.9. Примерная тематика коллоквиумов
Не предусмотрено.
9. СООТНОШЕНИЕ РАЗДЕЛОВ, ТЕМ ДИСЦИПЛИНЫ И ПРИМЕНЯЕМЫХ
ТЕХНОЛОГИЙ ОБУЧЕНИЯ
31
32.
Р1*
Р3
*
Р4
*
Р5
*
Р6
*
Р7
*
Р8
*
Другие (указать, какие)
Вебинары и
видеоконференции
Асинхронные webконференции и семинары
Совместная работа и
разработка контента
Виртуальные практикумы
и тренажеры
Дистанционные
образовательные технологии и
электронное обучение
Сетевые учебные курсы
Другие (указать, какие)
Командная работа
Проблемное обучение
Деловые игры
Кейс-анализ
Код раздела, темы
дисциплины
Проектная работа
Активные методы обучения
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ
(Приложение 1)
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХ
НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ (Приложение 2)
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ (Приложение 3)
9. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ
ДИСЦИПЛИНЫ
9.1.Рекомендуемая литература
9.1.1.Основная литература
1. Бибиков Ю.Н. Курс обыкновенных дифференциальных уравнений. С-Птб. Изд-во
«Лань». 2014 304 с. . (ЗНБ УрФУ).
2. Демидович Б.П. Лекции по математической теории устойчивости. 2014. С-Птб.
Изд-во «Лань». 480 с. . (ЗНБ УрФУ).
3. Ефимов А.В. Сборник задач по математике для втузов. Ч. 2. / А.В. Ефимов, А.Ф.
Каракулин, С.М. Коган и др – М.: Физматлит, 2003г. (ЗНБ УрФУ).
4. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям / А.Ф.
Филиппов. М.; Ижевск: РХД. 2004г. 176 с. (ЗНБ УрФУ).
5. Филиппов А.Ф. Введение в теорию дифференциальных уравнений / А.Ф. Филиппов.
М.: ЛЕНАНД. 2015г. 235 с. (ЗНБ УрФУ).
6. Шолохович Ф.А. Лекции по дифференциальным уравнениям. Университетский
курс. / Ф.А. Шолохович. Екатеринбург, Уральское издательство. 2005. . (ЗНБ
УрФУ).
9.1.2.Дополнительная литература
32
33.
1. Бугров Я.С. Дифференциальные уравнения. Кратные интегралы. Ряды. Функциикомплексного переменного. / Я.С. Бугров, С.М. Никольский. М.: Наука, 1989г.
(ЗНБ УрФУ).
2. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. / Л.С. Понтрягин –
М.: Наука. 1982г. . (ЗНБ УрФУ).
9.2.Методические разработки
1. Сесекин А.Н. Дифференциальные уравнения. Контрольные задания для студентов
дневной формы обучения специальности 230401 – Прикладная математика. / А.Н.
Сесекин. Изд-во УГТУ-УПИ. 2006.
2. Голикова Е.А. Дифференциальные уравнения и ряды в примерах и задачах / Е.А.
Голикова, А.С. Соболева. Учебное пособие. . Изд-во УГТУ-УПИ. 2009.
3. Гребенщиков Б.Г. Устойчивость и оптимальная стабилизация систем
дифференциальных уравнений / Б.Г. Гребенщиков, Н.В. Гредасова, О.Г.
Матвийчук, А.Б. Ложников, А.Н. Сесекин. УрФУ. 2016. 120 с.
9.3.Программное обеспечение
Математический пакет Mathcad, математический пакет MatLab.
9.4. Базы данных, информационно-справочные и поисковые системы
http://poiskknig.ru – электронная библиотека учебников Мех-Мата МГУ, Москва
http://www.mathnet.ru. - общероссийский математический портал
http://onlinelibrary.wiley.com - научные журналы издательства Wiley&Sons
http://www.sciencedirect.com - научные журналы издательства Elsevier
http://lib.urfu.ru – зональная научная библиотека УрФУ
9.5.Электронные образовательные ресурсы
Портал информационно - образовательных ресурсов УрФУ http://study.ustu.ru
10. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Сведения об оснащенности дисциплины специализированным и лабораторным
оборудованием
Учебный, лекционный класс (Т-1202):
Проектор, экран.
Компьютерный класс (Т-1208):
Компьютеры – 12 шт., объединены в локальную сеть с выходом в Интернет.
Мультимедийное оборудование (мультимедийный проектор, экран).
33
34.
ПРИЛОЖЕНИЕ 1к рабочей программе дисциплины
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В
РАМКАХ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
6.1. Весовой коэффициент значимости дисциплины –
6.2.Процедуры текущей и промежуточной аттестации по дисциплине
3 семестр
1.Лекции: коэффициент значимости совокупных результатов лекционных занятий – 0,6
Текущая аттестация на лекциях
Сроки –
Максималь
семестр,
ная оценка
учебная
в баллах
неделя
Экспертиза конспектов
3, 1-17
100
Весовой коэффициент значимости результатов текущей аттестации по лекциям – 0,4
Промежуточная аттестация по лекциям – экзамен
Весовой коэффициент значимости результатов промежуточной аттестации по лекциям –
0,6
2. Практические/семинарские занятия: коэффициент значимости совокупных
результатов практических/семинарских занятий – 0,4
Текущая аттестация на практических/семинарских
Сроки –
Максималь
занятиях
семестр,
ная оценка
учебная
в баллах
неделя
Работа на практических занятиях
3, 1-17
28
Домашняя работа 1
3, 1-17
16
Домашняя работа 2
3, 1-17
16
Контрольная работа 1
3, 1-17
20
Контрольная работа 2
3, 1-17
20
Весовой коэффициент значимости результатов текущей аттестации по
практическим/семинарским занятиям– 1
Промежуточная аттестация по практическим/семинарским занятиям–
Весовой коэффициент значимости результатов промежуточной аттестации по
практическим/семинарским занятиям– 0
3. Лабораторные занятия: коэффициент значимости совокупных результатов
лабораторных занятий – не предусмотрено
4 семестр
1.Лекции: коэффициент значимости совокупных результатов лекционных занятий – 0,6
Текущая аттестация на лекциях
Сроки –
Максималь
семестр,
ная оценка
учебная
в баллах
неделя
Экспертиза конспектов
4, 1-8
100
Весовой коэффициент значимости результатов текущей аттестации по лекциям – 0,4
Промежуточная аттестация по лекциям – экзамен
Весовой коэффициент значимости результатов промежуточной аттестации по лекциям –
0,6
2. Практические/семинарские занятия: коэффициент значимости совокупных
результатов практических/семинарских занятий – 0,4
Текущая аттестация на практических/семинарских
Сроки –
Максималь
34
35.
занятияхсеместр,
ная оценка
учебная
в баллах
неделя
Работа на практических занятиях
4, 9-17
40
Домашняя работа 1
4, 9-17
20
Контрольная работа 1
4, 9-17
20
Контрольная работа 2
4, 9-17
20
Весовой коэффициент значимости результатов текущей аттестации по
практическим/семинарским занятиям– 1
Промежуточная аттестация по практическим/семинарским занятиям–
Весовой коэффициент значимости результатов промежуточной аттестации по
практическим/семинарским занятиям– 0
3. Лабораторные занятия: коэффициент значимости совокупных результатов
лабораторных занятий – не предусмотрено
6.3. Процедуры текущей и промежуточной аттестации курсовой работы/проекта
Не предусмотрено
6.4. Коэффициент значимости семестровых результатов освоения дисциплины
Порядковый номер семестра по учебному
Коэффициент значимости результатов
плану, в котором осваивается дисциплина
освоения дисциплины в семестре
Семестр 3
0,6
Семестр 4
0,4
*В случае проведения промежуточной аттестации по дисциплине (экзамена, зачета) методом
тестирования используются официально утвержденные ресурсы: АПИМ УрФУ, СКУД УрФУ,
имеющие статус ЭОР УрФУ; ФЭПО (www.фэпо.рф); Интернет-тренажеры (www.i-exam.ru).
35
36.
ПРИЛОЖЕНИЕ 2к рабочей программе дисциплины
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХ
НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
сайте ФЭПО http://fepo.i-exam.ru.
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
сайте Интернет-тренажеры http://training.i-exam.ru.
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
портале СМУДС УрФУ.
В связи с отсутствием Дисциплины и ее аналогов, по которым возможно
тестирование, на сайтах ФЭПО, Интернет-тренажеры и портале СМУДС УрФУ,
тестирование в рамках НТК не проводится.
36
37.
ПРИЛОЖЕНИЕ 3к рабочей программе дисциплины
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
8.1. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ КОНТРОЛЬНО-ОЦЕНОЧНЫХ
МЕРОПРИЯТИЙ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО
ДИСЦИПЛИНЕ В РАМКАХ БРС
В рамках БРС применяются утвержденные на кафедре критерии оценивания
достижений студентов по каждому контрольно-оценочному мероприятию. Система критериев
оценивания, как и при проведении промежуточной аттестации по модулю, опирается на три
уровня освоения компонентов компетенций: пороговый, повышенный, высокий.
Компоненты
Признаки уровня освоения компонентов компетенций
компетенций
пороговый
повышенный
высокий
Студент демонстрирует
Студент демонстрирует Студент может
Знания
знание-знакомство,
аналитические знания:
самостоятельно
знание-копию: узнает
уверенно воспроизводит извлекать новые знания
объекты, явления и
и понимает полученные из окружающего мира,
понятия, находит в них
знания, относит их к той творчески их
различия, проявляет
или иной
использовать для
знание источников
классификационной
принятия решений в
получения информации,
группе, самостоятельно новых и нестандартных
может осуществлять
систематизирует их,
ситуациях.
самостоятельно
устанавливает
репродуктивные действия взаимосвязи между
над знаниями путем
ними, продуктивно
самостоятельного
применяет в знакомых
воспроизведения и
ситуациях.
применения информации.
Студент умеет корректно
Студент умеет
Студент умеет
Умения
выполнять предписанные самостоятельно
самостоятельно
действия по инструкции,
выполнять действия
выполнять действия,
алгоритму в известной
(приемы, операции) по
связанные с решением
ситуации, самостоятельно решению нестандартных исследовательских
выполняет действия по
задач, требующих
задач, демонстрирует
решению типовых задач,
выбора на основе
творческое
требующих выбора из
комбинации известных использование умений
числа известных методов, методов, в
(технологий)
в предсказуемо
непредсказуемо
изменяющейся ситуации
изменяющейся ситуации
Студент имеет
Студент имеет
Личностные Студент имеет низкую
мотивацию учебной
выраженную мотивацию развитую мотивацию
качества
деятельности, проявляет
учебной деятельности,
учебной и трудовой
безразличное,
демонстрирует
деятельности,
безответственное
позитивное отношение к проявляет
отношение к учебе,
обучению и будущей
настойчивость и
порученному делу
трудовой деятельности, увлеченность,
проявляет активность.
трудолюбие,
самостоятельность,
творческий подход.
37
38.
8.2. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИПРИ ИСПОЛЬЗОВАНИИ НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ
При проведении независимого тестового контроля как формы промежуточной
аттестации применяется методика оценивания результатов, предлагаемая разработчиками
тестов. Процентные показатели результатов независимого тестового контроля переводятся в
баллы промежуточной аттестации по 100-балльной шкале в БРС:
в случае балльной оценки по тесту (блокам, частям теста) переводится процент набранных
баллов от общего числа возможных баллов по тесту;
при отсутствии балльной оценки по тесту переводится процент верно выполненных
заданий теста, от общего числа заданий.
8.3. ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ
И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
8.3.1. Примерные задания для проведения домашних работ
3 семестр
Домашняя работа № 1.
2
Решить дифференциальное уравнение: y 2 xy 2 xe x .
Домашняя работа № 2.
Найти общее решение дифференциального уравнения: y 4 y 4 y 2e x .
4 семестр
Домашняя работа № 1.
Изобразить фазовый портрет системы:
x y x 2 x,
y 3x x 2 y.
8.3.2. Примерные контрольные задачи в рамках учебных занятий
3 семестр
Контрольная работа № 1.
Решить дифференциальное уравнение: x y 3 y 2.
Контрольная работа № 2.
Найти общее решение системы дифференциальных уравнений:
x y z ,
y z x,
z x y.
4 семестр
Контрольная работа № 1.
Установить тип точек покоя системы:
x y,
y sin( x y ).
Контрольная работа № 2.
Исследовать на устойчивость систему
с помощью функции Ляпунова.
38
39.
8.3.3. Примерные контрольные кейсы8.3.4. Перечень примерных вопросов для зачета
1. Определение устойчивости по Ляпунову решения дифференциального уравнения.
Определение асимптотической устойчивости.
2. Простейшие типы точек покоя.
3. Метод функций Ляпунова. Первая теорема Ляпунова.
4. Вторая теорема Ляпунова.
5. Третья теорема Ляпунова.
6. Необходимое и достаточное условие устойчивости линейной неоднородной системы.
7. Необходимое и достаточное условие устойчивости линейной однородной системы.
8. Устойчивость и асимптотическая устойчивость систем линейных дифференциальных
уравнений с постоянной матрицей.
9. Критерий Гурвица (без доказательства).
10. Неравенство Гронуолла.
11. Устойчивость по первому приближению.
12. Оптимальная стабилизация динамических систем.
8.3.5. Перечень примерных вопросов для экзамена
1. Задачи, приводимые к дифференциальным уравнениям.
2. Основные понятия: первый интеграл, общий интеграл, задача Коши. Поле направлений.
3. Дифференциальные уравнения с разделяющимися переменными.
4. Однородные дифференциальные уравнения.
5. Линейные дифференциальныe ypавнeния (метод Бернулли, метод вариации произвольных
постоянных).
6. Уравнение Бернулли.
7. Дифференциальное уравнение в полных дифференциалах.
8. Интегрирующий множитель.
9. Теорема существования и единственности решения дифференциального уравнения.
10. Продолжимость решений дифференциальных уравнений.
11. Особые решения. Огибающая семейства кривых.
12. Уравнения, не разрешенные относительно производной. Общий метод введения параметра.
Уравнения Лагранжа и Клеро.
13. Теорема существования и единственности решения дифференциального уравнения n-го
порядка (без доказательства).
14. Понижение порядка дифференциального уравнения.
15. Определитель Вронского. Критерий линейной зависимости системы функций.
16. Критерий линейной независимости решений линейного однородного дифференциального
уравнения n-го порядка.
17. Структура общего решения линейного однородного дифференциального уравнения n-го
порядка.
18. Структура общего решения линейного неоднородного дифференциального уравнения n-го
порядка.
19. Построение общего решения линейного однородного дифференциального уравнения n-го
порядка с постоянными коэффициентами.
20. Метод вариации произвольных постоянных.
21. Уравнение Эйлера.
22. Методы нахождения частных решений неоднородных линейных дифференциальных
уравнений n-го порядка с постоянными коэффициентами.
23. Теорема существования и единственности решения системы дифференциальных
уравнений n-го порядка (без доказательства).
24. Интегрирование систем дифференциальных уравнений путем сведения к одному
дифференциальному уравнению более высокого порядка.
25. Структура общего решения однородной системы линейных дифференциальных уравнений.
26. Общее решение линейной однородной системы дифференциальных уравнений с
постоянными коэффициентами.
39
40.
27. Структура общего решения линейной неоднородной системы дифференциальныхуравнений.
28. Метод вариации произвольных постоянных для системы линейных дифференциальных
уравнений.
8.3.6. Ресурсы АПИМ УрФУ, СКУД УрФУ для проведения тестового контроля в рамках
текущей и промежуточной аттестации
не используются
8.3.7. Ресурсы ФЭПО для проведения независимого тестового контроля
не используются
8.3.8. Интернет-тренажеры
не используются
40
41.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное автономное образовательное учреждение
высшего образования
«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО И ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Перечень сведений о рабочей программе
дисциплины
Модуль
Специальные главы математики
Образовательная программа
Прикладная математика
Учетные данные
Код модуля 1127561
Код ОП
01.03.04/01.01
Учебный план в ЕИСУ № 6104
Код направления и уровня
подготовки
01.03.04
Направление подготовки
Прикладная математика
Уровень подготовки
Бакалавриат
ФГОС ВО
Реквизиты приказа Минобрнауки
РФ об утверждении ФГОС ВО:
12 марта 2015 г., № 208
Екатеринбург, 2017
41
42.
Рабочая программа дисциплины составлена авторами:№
п/п
1
Сесекин
Александр Николаевич
Ученая степень,
ученое звание
Д-р физ.- мат.
наук, профессор
2
Полищук
Ефим Григорьевич
Канд. физ.-мат.
наук, доцент
Доцент
3
Гредасова
Надежда Викторовна
Канд. физ.-мат.
наук
Доцент
ФИО
Руководитель модуля
Должность
профессор
Кафедра
Подпись
Прикладн
ая
математи
ка
Прикладн
ая
математи
ка
Прикладн
ая
математи
ка
А.Н. Сесекин
Рекомендовано учебно-методическим советом Уральского энергетического института
Председатель учебно-методического совета
Протокол № ______ от __________ г.
Е.В. Черепанова
Согласовано:
Дирекция образовательных программ
Р.Х. Токарева
42
43.
3. ОБЩАЯ ХАРАКТЕРИСТИКА ДИСЦИПЛИНЫ «Теория функцийкомплексного переменного и операционное исчисление»
1.3.Аннотация содержания дисциплины
Дисциплина относится к модулю «Специальные главы математики» (базовая часть).
Дисциплина изучается в 3 семестре. В модуль входят следующие дисциплины:
Функциональный анализ (4 семестр), Обыкновенные дифференциальные уравнения и теория
устойчивости (3,4 семестры), Дискретная математика (3,4 семестры), Теория вероятностей и
математическая статистика (4 семестр), Введение в специальность (3 семестр).
Дисциплина посвящена изучению основ теории функций комплексной переменной и
операционного исчисления. В курсе рассматриваются следующие темы: основные
элементарные функции и их свойства; предел, непрерывность, дифференцирование и
интегрирование функций комплексного переменного; ряды в комплексной области; теория
вычетов; конформные отображения, преобразования Лапласа.
1.2. Язык реализации программы – русский
1.3. Планируемые результаты обучения по дисциплине
Результатом обучения в рамках дисциплины является формирование у студента
следующих компетенций:
ОПК-1 - готовность к самостоятельной работе;
ПК-9 - способность выявить естественнонаучную сущность проблем, возникающих в
ходе профессиональной деятельности, готовностью использовать для их решения
соответствующий естественнонаучный аппарат;
ПК-10 - готовность применять математический аппарат для решения поставленных задач,
способностью применить соответствующую процессу математическую модель и проверить ее
адекватность, провести анализ результатов моделирования, принять решение на основе
полученных результатов;
ПК-12 - способность самостоятельно изучать новые разделы фундаментальных наук;
В результате освоения дисциплины студент должен:
Знать: основные положения теории функций комплексного переменного и
операционного исчисления
Уметь:
- определять возможности применения теоретических положений и методов теории функций
комплексного переменного для постановки и решения конкретных задач;
- решать основные задачи на вычисление интегралов при помощи вычетов, на разложение
функций в ряды Тейлора и Лорана;
- применять методы операционного исчисления к решению дифференциальных и
интегральных уравнений.
Владеть (демонстрировать навыки и опыт деятельности):
- стандартными методами теории функций комплексного переменного и операционного
исчисления и их применением к решению прикладных задач.
9.4. Объем дисциплины
Очная форма обучения
43
44.
Объем дисциплины№
п/
п
Виды учебной работы
1.
2.
3.
4.
5.
6.
7.
8.
Распределение объема
дисциплины по семестрам (час.)
Всего
часов
В т.ч.
контактн
ая работа
(час.)*
3
Аудиторные занятия
Лекции
Практические занятия
Лабораторные работы
Самостоятельная работа студентов,
включая все виды текущей
аттестации
Промежуточная аттестация
50
34
17
50
34
17
50
34
17
75
7,65
75
18
2,33
Общий объем по учебному плану,
час.
Общий объем по учебному плану,
з.е.
144
60,98
Э,18
144
4
4
*Контактная работа составляет:
в п/п 2,3,4 - количество часов, равное объему соответствующего вида занятий;
в п.5 – количество часов, равное сумме объема времени, выделенного преподавателю на консультации в
группе (15% от объема аудиторных занятий) и объема времени, выделенного преподавателю на руководство
курсовой работой/проектом одного студента, если она предусмотрена.
в п.6 – количество часов, равное сумме объема времени, выделенного преподавателю на проведение
соответствующего вида промежуточной аттестации одного студента и объема времени, выделенного в рамках
дисциплины на руководство проектом по модулю (если он предусмотрен) одного студента.
10. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
Код
раздела,
темы
Раздел, тема
дисциплины*
Р1
Комплексные числа
Р2
Последовательности и
ряды
Р3
Функции комплексного
Содержание
Понятие комплексного числа. Некоторые частные виды
комплексных чисел. Геометрическое изображение
комплексного числа. Модуль и аргумент его. Неравенства,
связанные с модулем. Различные формы записи
комплексных чисел и действия над ними в этих формах.
Извлечение корня. Свойства комплексно-сопряженных
чисел. Понятие окрестности точки. Определение
изолированной, внутренней и граничной точек множества.
Определение открытого, связного, ограниченного и
замкнутого
множества.
Определение
области
(односвязной и многосвязной).
Понятие последовательности комплексных чисел. Предел
последовательности. Теорема о необходимом и
достаточном условии сходимости последовательности.
Числовые ряды в комплексной области. Основные
понятия. Теорема о необходимом и достаточном условии
сходимости числового ряда. Теорема о достаточном
условии абсолютной сходимости ряда. Степенные ряды.
Основные понятия. Теорема Абеля. Нахождение области
сходимости степенного ряда.
Понятие ФКП (функции комплексного переменного).
44
45.
переменногоР4
Аналитические функции
Нахождение образа множества при отображении
w f (z ) . Важнейшие элементарные ФКП и их свойства.
Формулы Эйлера. Формулы связи гиперболических
функций с показательной и тригонометрическими. Предел
ФКП в точке. Теорема о необходимом и достаточном
условии существования предела функции в точке.
Основные теоремы теории пределов (без доказательства).
Непрерывность ФКП в точке и на множестве. Теорема о
необходимом и достаточном условии непрерывности
ФКП в точке. Теоремы о непрерывных функциях (без
доказательства). Дифференцирование ФКП. Определение
производной ФКП в точке. Основные правила
дифференцирования. Необходимое и достаточное условия
дифференцируемости функции в точке (условия КошиРимана).
Формулы
для
вычисления
f (z ) .
Интегрирование ФКП. Определение интеграла от ФКП.
Теорема существования его. Формула для вычисления его.
Свойства интеграла от ФКП.
Определение аналитической функции комплексного
переменного в точке и области. Понятие особой и
изолированной точки. Аналитичность элементарных
функций. Понятие гармонической в области функции
действительного
переменного.
Связь
между
гармоническими и аналитическими функциями.
Восстановление
аналитической
функции
по
известной ее действительной или мнимой части.
Геометрический смысл модуля и аргумента
производной.
Конформные
отображения.
Отображения, задаваемые с помощью линейной,
дробно-линейной, показательной и степенной
функций. Интегрирование аналитической ФКП.
Интегральная теорема Коши. Следствие из этой
теоремы. Обобщение интегральной теоремы Коши на
случай многосвязной области. Следствие из этой
теоремы.
Понятие
первообразной
ФКП.
Существование
первообразной
для
любой
аналитической в односвязной области функции.
Аналог формулы Ньютона-Лейбница. Интегральные
формулы Коши. Вывод их на случай односвязной и
многосвязной области. Ряд Тейлора. Теорема о
разложении однозначной аналитической функции в т.
z 0 в ряд Тейлора по степеням z z 0 . Ряд Лорана.
Теорема о разложении аналитической в кольце
функции в ряд Лорана.
Классификация
изолированных
особых
точек.
Эквивалентность двух определений каждого из видов
особых точек. Изучение поведения ФКП в бесконечности.
Понятие вычета функции в изолированной особой точке
z 0 . Его связь с рядом Лорана функции по степеням
Р5
Вычеты и их приложения
z z 0 . Вычисление вычетов функции для разных типов
особых точек. Основная теорема о вычетах. Следствие из
нее. Вычисление некоторых контурных интегралов ФКП с
помощью вычетов. Вычисление некоторых определенных
интегралов действительной переменной с помощью
вычетов
45
46.
Р6Операционное исчисление
Определение оригинала и его свойства. Определение
изображения. Теорема существования изображения.
Изображение простейших оригиналов: (t ) и e t (t ) .
Простейшие
свойства
преобразования
Лапласа:
однородность,
аддитивность,
подобие,
дифференцирование и интегрирование оригинала и
изображения. Теоремы о сдвиге аргументов оригинала и
изображения. Изображение периодического оригинала.
Свертка функций. Ее свойства. Теорема Бореля.
Восстановление
оригинала
по
известному
ее
изображению. Обращение преобразования Лапласа.
Вычисление оригинала с помощью вычетов. Применение
операционного исчисления к решению линейных
дифференциальных уравнений и систем с постоянными
коэффициентами. Решение интегральных уравнений.
11. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ
3.3. Распределение аудиторной нагрузки и мероприятий самостоятельной работы по
разделам дисциплины
Очная форма обучения
46
47.
Объем модуля (зач.ед.): 28Объем дисциплины (4 зач.ед.): 3
Самостоятельная работа: виды, количество и объемы мероприятий
1
1
6
6
1
1
8
В т.ч. промежуточная аттестация
47
18
Подго
товка
в
рамка
х
дисци
плины
к
проме
жуточ
ной
аттест
ации
по
модул
ю
(час.)
Проект по модулю
2
2
Экзамен
1
Зачет
Контрольная работа*
2
Коллоквиум*
Всего (час.)
Курсовой проект*
Курсовая работа*
18
Перевод инояз. литературы*
17
Домашняя работа на иностр.
языке*
34
Расчетно-графическая работа*
6
Расчетная работа, разработка
программного продукта*
3
3
4
Проектная работа*
6
6
8
1
1
Реферат, эссе, творч. работа*
4
6
6
Графическая работа*
8
Домашняя работа*
1
2
Всего (час.)
Практ., семинар. занятие
2
4
Лабораторное занятие
Лекция
12
3
2
1
9
3
Комплексные числа
18
6
4
2
12
6
Последовательности и
ряды
26
12
8
4
14
12
Р3
Функции комплексного
переменного
24
9
6
3
15
9
Р4
Аналитические функции
20
9
6
3
11
9
Р5
Вычеты и их приложения
26
12
8
4
14
12
Р6
Операционное исчисление
Всего (час), без учета
126
51
34
17
75
51
промежуточной
аттестации:
Всего по дисциплине
144
51
93
(час.):
*Суммарный объем в часах на мероприятие
указывается в строке «Всего (час.) без учета промежуточной аттестации
Р1
Р2
Выполнение самостоятельных внеаудиторных работ
(колич.)
Н/и семинар, семинар-конфер.,
коллоквиум (магистратура)
Подготовка к аудиторным
занятиям (час.)
Подготов
ка к
промежут
очной
аттестац
ии по
дисципли
не (час.)
Интегрированный экзамен по модулю
Подготовка к
контрольным
мероприятиям
текущей
аттестации
(колич.)
Всего (час.)
Всего самостоятельной работы студентов (час.)
Лабораторные работы
Практические занятия
Лекции
Всего по разделу, теме (час.)
Код раздела, темы
Наименование раздела,
темы
Всего аудиторной работы (час.)
Аудиторные
занятия (час.)
Раздел дисциплины
48.
12. ОРГАНИЗАЦИЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ, САМОСТОЯТЕЛЬНОЙ РАБОТЫПО ДИСЦИПЛИНЕ
6.5. Лабораторные работы
не предусмотрено
Код
раздела,
темы
6.6. Практические занятия
Номер
занятия
1.
2.
3.
4.
1
2
3
5.
6.
5
6
4
Время на
проведение
занятия (час.)
Тема занятия
Комплексные числа
Последовательности и ряды
Функции комплексного переменного
Аналитические функции комплексного
переменного
Вычеты и их приложения
Операционное исчисление
1
2
4
3
Всего:
3
4
17
5. 4.3.Примерная тематика самостоятельной работы
4.3.7. Примерный перечень тем домашних работ
1. Комплексные числа
2. Последовательности и ряды
3. Аналитические функции
4.3.8. Примерный перечень тем графических работ
не предусмотрено
4.3.9. Примерный перечень тем рефератов (эссе, творческих работ)
не предусмотрено
4.3.4 Примерная тематика индивидуальных или групповых проектов
не предусмотрено
4.3.12. Примерный перечень тем расчетных работ (программных продуктов)
не предусмотрено
4.3.13. Примерный перечень тем расчетно-графических работ
не предусмотрено
4.3.14. Примерный перечень тем курсовых проектов (курсовых работ)
не предусмотрено
12.4.1. Примерная тематика контрольных работ
1. Функции комплексного переменного
2. Вычеты
3. Операционное исчисление
4.3.9. Примерная тематика коллоквиумов
не предусмотрено
13. СООТНОШЕНИЕ РАЗДЕЛОВ, ТЕМ ДИСЦИПЛИНЫ И ПРИМЕНЯЕМЫХ
ТЕХНОЛОГИЙ ОБУЧЕНИЯ
Код раздела, темы
Активные методы обучения
48
Дистанционные
образовательные технологии и
49.
Р1-Р6Другие (указать, какие)
Вебинары и
видеоконференции
Асинхронные webконференции и семинары
Совместная работа и
разработка контента
Виртуальные практикумы
и тренажеры
Сетевые учебные курсы
Другие (указать, какие)
Командная работа
Проблемное обучение
Деловые игры
Кейс-анализ
электронное обучение
Проектная работа
дисциплины
*
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ
(Приложение 1)
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХ
НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ (Приложение 2)
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ (Приложение 3)
9. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ
ДИСЦИПЛИНЫ
9.1.Рекомендуемая литература
9.1.1.Основная литература
1. Карасев, И. П. Теория функций комплексного переменного / И.П. Карасев .— Москва :
Физматлит, 2008 .— 215 с. — ISBN 978-5-9221-0960-4 .—
<URL:http://biblioclub.ru/index.php?page=book&id=68139>.
2.Сборник задач по математике для втузов : учеб. пособие: в 4 ч. Ч. 3 / Под ред. А.В.
Ефимова, А.С. Поспелова. — 5-е изд., перераб. — М.: ФИЗМАТЛИТ, 2007. — 544 с. — ISBN
5-94052-131-2. — ISBN 5-94052-130-4. ЗНБ УрФУ.
3. Письменный, Д. Т. Конспект лекций по высшей математике : [полный курс] / Д. Т.
Письменный .— 12-е изд. — М : АЙРИС-ПРЕСС, 2014 .— 608 с.— ISBN 978-5-8112-5257-2
ЗБН УрФУ.
4. Араманович, И.Г. Функции комплексного переменного. Операционное исчисление.
Теория устойчивости : учеб. пособие для вузов / И. Г. Араманович, Г. Л. Лунц, Эльсгольц .—
2-е изд., перераб., доп. — М. : Наука, 1968 .— 416 с. ЗНБ УрФУ.
9.1.2.Дополнительная литература
1. Бугров, Я. С. Высшая математика. Дифференциальные уравнения. Кратные интегралы.
Ряды. Функции комплексного переменного : учебник для вузов / Я. С. Бугров, С. М.
Никольский .— 4-е изд., улучш. — Ростов н/Д : Феникс, 1998 .— 512 с. — ISBN 5-222-002152. ЗНБ УрФУ.
2. Маркушевич, А.И. Комплексные числа и конформные отображения / Маркушевич А. И.
— Москва : Государственное издательство технико-теоретической литературы, 1954 .— 52
с.— ISBN 978-5-4458-6628-2 .— <URL:http://biblioclub.ru/index.php?page=book&id=228167>.
3. Сидоров, Ю. В. Лекции по теории функций комплексного переменного : учебник для
инж.-физ. и физ.-техн. спец. вузов / Ю. В. Сидоров, М. В. Федорюк, М. И. Шабунин .— 2-е
изд., перераб. и доп. — М. : Наука, 1982 .— 488 с. ЗНБ УрФУ.
4. Привалов, И.И. Введение в теорию функций комплексного переменного : учеб. для
49
50.
вузов / И. И. Привалов ; под ред. В. А. Садовничего .— 14-е изд., стер. — М.: Высшая школа,1999 .— 432 с.— ISBN 5-06-003612-Х. ЗНБ УрФУ.
5. Пантелеев, А.В. Теория функций комплексного переменного и операционное
исчисление в примерах и задачах : учеб. пособие / А. В. Пантелеев, А. С. Якимова .— М. :
Высшая школа, 2001 .— 445 с.— ISBN 5-06-004135-2. ЗНБ УрФУ.
9.2.Методические разработки
1. Функции комплексного переменного: Методические указания по курсу «Высшая
математика» / В.И. Зенков, Е.Г. Полищук. Екатеринбург: УГТУ, 1995г.
9.3.Программное обеспечение
Не используется
9.4. Базы данных, информационно-справочные и поисковые системы
http://study.urfu.ru – портал информационно-образовательных ресурсов УрФУ
http://lib.urfu.ru – зональная научная библиотека УрФУ
http://poiskknig.ru – электронная библиотека учебников Мех-Мата МГУ, Москва
http://www.mathnet.ru. - общероссийский математический портал
http://onlinelibrary.wiley.com - научные журналы издательства Wiley&Sons
http://www.sciencedirect.com - научные журналы издательства Elsevier
https://www.coursera.org/ – массовые открытые онлайн-курсы;
https://www.edx.org/ – массовые открытые онлайн-курсы;
https://openedu.ru/ – национальная платформа открытого образования;
9.5.Электронные образовательные ресурсы
не используется
10. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Сведения об оснащенности дисциплины специализированным и лабораторным
оборудованием
Мультимедийная аудитория Т-1208: 10 ПК, проектор; мультимедийная аудитория Т1202б: 10 ПК, проектор, интерактивная доска.
50
51.
ПРИЛОЖЕНИЕ 1к рабочей программе дисциплины
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В
РАМКАХ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
6.1. Весовой коэффициент значимости дисциплины –
6.2.Процедуры текущей и промежуточной аттестации по дисциплине
1.Лекции: коэффициент значимости совокупных результатов лекционных занятий – 0.6
Текущая аттестация на
Сроки –
Максималь
семестр,
ная оценка
учебная
в баллах
неделя
Экспертиза конспекта
3, 1-17
100
Весовой коэффициент значимости результатов текущей аттестации по лекциям – 0.4
Промежуточная аттестация по лекциям – экзамен
Весовой коэффициент значимости результатов промежуточной аттестации по лекциям –
0.6.
2. Практические/семинарские занятия: коэффициент значимости совокупных
результатов практических/семинарских занятий – 0,4
Текущая аттестация на практических/семинарских
Сроки –
Максималь
занятиях
семестр,
ная оценка
учебная
в баллах
неделя
Домашняя работа 1
3,1-8
16
Домашняя работа 2
3,1-8
8
Домашняя работа 3
3,1-8
6
Контрольная работа 1
3,1-8
20
Контрольная работа 2
3,1-8
10
Контрольная работа 3
3,1-8
10
Работа на практических занятиях
3,1-8
28
Весовой коэффициент значимости результатов текущей аттестации по
практическим/семинарским занятиям– 1.0
Промежуточная аттестация по практическим/семинарским занятиям– не предусмотрено
Весовой коэффициент значимости результатов промежуточной аттестации по
практическим/семинарским занятиям– 0.0
3. Лабораторные занятия: коэффициент значимости совокупных результатов
лабораторных занятий – не предусмотрено
6.3. Процедуры текущей и промежуточной аттестации курсовой работы/проекта
Не предусмотрено
6.4. Коэффициент значимости семестровых результатов освоения дисциплины
Порядковый номер семестра по учебному
Коэффициент значимости результатов
плану, в котором осваивается дисциплина
освоения дисциплины в семестре
Семестр 3
1.0
*В случае проведения промежуточной аттестации по дисциплине (экзамена, зачета) методом
тестирования используются официально утвержденные ресурсы: АПИМ УрФУ, СКУД УрФУ,
имеющие статус ЭОР УрФУ; ФЭПО (www.фэпо.рф); Интернет-тренажеры (www.i-exam.ru).
51
52.
ПРИЛОЖЕНИЕ 2к рабочей программе дисциплины
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХ
НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
сайте ФЭПО http://fepo.i-exam.ru.
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
сайте Интернет-тренажеры http://training.i-exam.ru.
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
портале СМУДС УрФУ.
В связи с отсутствием Дисциплины и ее аналогов, по которым возможно
тестирование, на сайтах ФЭПО, Интернет-тренажеры и портале СМУДС УрФУ,
тестирование в рамках НТК не проводится.
52
53.
ПРИЛОЖЕНИЕ 3к рабочей программе дисциплины
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
8.1. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ КОНТРОЛЬНО-ОЦЕНОЧНЫХ
МЕРОПРИЯТИЙ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО
ДИСЦИПЛИНЕ В РАМКАХ БРС
В рамках БРС применяются утвержденные на кафедре критерии оценивания
достижений студентов по каждому контрольно-оценочному мероприятию. Система критериев
оценивания, как и при проведении промежуточной аттестации по модулю, опирается на три
уровня освоения компонентов компетенций: пороговый, повышенный, высокий.
Компоненты
Признаки уровня освоения компонентов компетенций
компетенций
пороговый
повышенный
высокий
Студент демонстрирует
Студент демонстрирует Студент может
Знания
знание-знакомство,
аналитические знания:
самостоятельно
знание-копию: узнает
уверенно воспроизводит извлекать новые знания
объекты, явления и
и понимает полученные из окружающего мира,
понятия, находит в них
знания, относит их к той творчески их
различия, проявляет
или иной
использовать для
знание источников
классификационной
принятия решений в
получения информации,
группе, самостоятельно новых и нестандартных
может осуществлять
систематизирует их,
ситуациях.
самостоятельно
устанавливает
репродуктивные действия взаимосвязи между
над знаниями путем
ними, продуктивно
самостоятельного
применяет в знакомых
воспроизведения и
ситуациях.
применения информации.
Студент умеет корректно
Студент умеет
Студент умеет
Умения
выполнять предписанные самостоятельно
самостоятельно
действия по инструкции,
выполнять действия
выполнять действия,
алгоритму в известной
(приемы, операции) по
связанные с решением
ситуации, самостоятельно решению нестандартных исследовательских
выполняет действия по
задач, требующих
задач, демонстрирует
решению типовых задач,
выбора на основе
творческое
требующих выбора из
комбинации известных использование умений
числа известных методов, методов, в
(технологий)
в предсказуемо
непредсказуемо
изменяющейся ситуации
изменяющейся ситуации
Студент имеет
Студент имеет
Личностные Студент имеет низкую
мотивацию учебной
выраженную мотивацию развитую мотивацию
качества
деятельности, проявляет
учебной деятельности,
учебной и трудовой
безразличное,
демонстрирует
деятельности,
безответственное
позитивное отношение к проявляет
отношение к учебе,
обучению и будущей
настойчивость и
порученному делу
трудовой деятельности, увлеченность,
проявляет активность.
трудолюбие,
самостоятельность,
творческий подход.
53
54.
8.2. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИПРИ ИСПОЛЬЗОВАНИИ НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ
При проведении независимого тестового контроля как формы промежуточной
аттестации применяется методика оценивания результатов, предлагаемая разработчиками
тестов. Процентные показатели результатов независимого тестового контроля переводятся в
баллы промежуточной аттестации по 100-балльной шкале в БРС:
в случае балльной оценки по тесту (блокам, частям теста) переводится процент набранных
баллов от общего числа возможных баллов по тесту;
при отсутствии балльной оценки по тесту переводится процент верно выполненных
заданий теста, от общего числа заданий.
8.3. ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ
И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
8.3.1. Примерные задания для проведения домашних работ
Домашняя работа № 1
1. Записать комплексное число z 1 i в тригонометрической и показательной
форме.
Домашняя работа № 2
n
1. Найти предел последовательности zn (1 3i) .
Домашняя работа № 3
1. Вычислить интеграл:
ez
|z| 1 z 2 2 z dz .
8.3.2. Примерные контрольные задачи в рамках учебных занятий
Контрольная работа № 1
3
2
1. Найти аналитическую функцию по заданной действительной части u x 3xy 2 .
Контрольная работа № 2
1. Найти особые точки и указать их характер
sin z
z z 1
2
2
2
.
Контрольная работа № 3
1. Найти частное решение дифференциального уравнения x 9 x e
2t
,
x 0 0, x 0 0.
удовлетворяющее заданным начальным условиям
8.3.3. Примерные контрольные кейсы
не предусмотрено
8.3.4. Перечень примерных вопросов для зачета
не предусмотрено
8.3.5. Перечень примерных вопросов для экзамена
1.
Понятие комплексного числа. Геометрическое изображение комплексного числа.
2.
Модуль и аргумент комплексного числа
3.
Различные формы записи комплексных чисел и действия над ними в этих формах.
4.
Извлечение корня.
5.
Понятие окрестности точки. Определение изолированной, внутренней и граничной
точек множества. Определение открытого, связного, ограниченного и замкнутого
множества. Определение области (односвязной и многосвязной).
6.
Понятие последовательности комплексных чисел. Предел последовательности
комплексных чисел.
54
55.
7.Теорема о необходимом и достаточном условии сходимости последовательности.
8.
Числовые ряды в комплексной области. Основные понятия.
9.
Теорема о необходимом и достаточном условии сходимости числового ряда.
10. Теорема о достаточном условии абсолютной сходимости ряда.
11. Степенные ряды. Основные понятия. Теорема Абеля. Нахождение области
сходимости степенного ряда
12. Понятие ФКП (функции комплексного переменного). Нахождение образа
множества при отображении w f (z ) .
13. Важнейшие элементарные ФКП и их свойства. Формулы Эйлера. Формулы связи
гиперболических функций с показательной и тригонометрическими.
14. Предел ФКП в точке. Теорема о необходимом и достаточном условии
существования предела функции в точке.
15. Основные теоремы теории пределов (без доказательства).
16. Непрерывность ФКП в точке и на множестве. Теорема о необходимом и
достаточном условии непрерывности ФКП в точке.
17. Теоремы о непрерывных функциях (без доказательства).
18. Дифференцирование ФКП. Определение производной ФКП в точке. Основные
правила дифференцирования.
19. Необходимое и достаточное условия дифференцируемости функции в точке
(условия Коши-Римана).
20. Формулы для вычисления f (z ) .
21. Интегрирование ФКП. Определение интеграла от ФКП. Теорема существования
его. Формула для вычисления его. Свойства интеграла от ФКП.
22. Определение аналитической функции комплексного переменного в точке и
области. Понятие особой и изолированной точки.
23. Аналитичность элементарных функций. Понятие гармонической в области
функции действительного переменного. Связь между гармоническими и аналитическими
функциями.
24. Восстановление аналитической функции по известной ее действительной или
мнимой части.
25. Геометрический смысл модуля и аргумента производной.
26. Конформные отображения. Отображения, задаваемые с помощью линейной,
дробно-линейной, показательной и степенной функций.
27. Интегрирование аналитической ФКП. Интегральная теорема Коши. Следствие из
этой теоремы.
28. Обобщение интегральной теоремы Коши на случай многосвязной области.
Следствие из этой теоремы.
29. Понятие первообразной ФКП. Существование первообразной для любой
аналитической в односвязной области функции. Аналог формулы Ньютона-Лейбница.
Интегральные формулы Коши.
30. Ряд Тейлора. Теорема о разложении однозначной аналитической функции в т. z 0 в
ряд Тейлора по степеням z z 0 .
31. Ряд Лорана. Теорема о разложении аналитической в кольце функции в ряд Лорана.
32. Классификация изолированных особых точек. Эквивалентность двух определений
каждого из видов особых точек.
33. Понятие вычета функции в изолированной особой точке z 0 . Его связь с рядом
Лорана функции по степеням z z 0 .
34. Вычисление вычетов функции для разных типов особых точек. Основная теорема о
вычетах. Следствие из нее.
35. Вычисление некоторых контурных интегралов ФКП с помощью вычетов.
36. Вычисление некоторых определенных интегралов действительной переменной с
помощью вычетов.
55
56.
37. Определение оригинала и его свойства.38. Определение изображения. Теорема существования изображения.
39. Изображение простейших оригиналов: (t ) и e t (t ) .
40. Простейшие свойства преобразования Лапласа: однородность, аддитивность,
подобие, дифференцирование и интегрирование оригинала и изображения. Теоремы о
сдвиге аргументов оригинала и изображения.
41. Изображение периодического оригинала. Свертка функций. Ее свойства. Теорема
Бореля.
42. Восстановление оригинала по известному ее изображению. Обращение
преобразования Лапласа.
43. Вычисление оригинала с помощью вычетов.
44. Применение операционного исчисления к решению линейных дифференциальных
уравнений и систем с постоянными коэффициентами.
45. Решение интегральных уравнений.
8.3.6. Ресурсы АПИМ УрФУ, СКУД УрФУ для проведения тестового контроля в рамках
текущей и промежуточной аттестации
не используются
8.3.7. Ресурсы ФЭПО для проведения независимого тестового контроля
не используются
8.3.8. Интернет-тренажеры
не используются
56
57.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное автономное образовательное учреждение
высшего образования
«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
ДИСКРЕТНАЯ МАТЕМАТИКА
Перечень сведений о рабочей программе
дисциплины
Модуль
Специальные главы математики
Образовательная программа
Прикладная математика
Учетные данные
Код модуля 1127561
Код ОП
01.03.04/01.01
Учебный план в ЕИСУ № 6104
Код направления и уровня
подготовки
01.03.04
Направление подготовки
Прикладная математика
Уровень подготовки
Бакалавриат
ФГОС ВО
Реквизиты приказа Минобрнауки
РФ об утверждении ФГОС ВО:
12 марта 2015 г., № 208
Екатеринбург, 2017
57
58.
Рабочая программа дисциплины составлена авторами:№ п/п
ФИО
1
Андреева
Ирина Юрьевна
Ученая степень,
ученое звание
Канд. физ.-мат.
наук, доцент
2
Гредасова Надежда
Викторовна
Канд. физ.-мат.
наук
Руководитель модуля
Должность
Доцент
Доцент
Кафедра
Подпись
Прикладн
ая
математи
ка
Прикладн
ая
математи
ка
А.Н. Сесекин
Рекомендовано учебно-методическим советом Уральского энергетического института
Председатель учебно-методического совета
Протокол № ______ от __________ г.
Е.В. Черепанова
Согласовано:
Дирекция образовательных программ
Р.Х. Токарева
58
59.
4. ОБЩАЯ ХАРАКТЕРИСТИКА ДИСЦИПЛИНЫ «ДИСКРЕТНАЯ МАТЕМАТИКА»1.4.Аннотация содержания дисциплины
Дисциплина относится к модулю «Специальные главы математики» (базовая часть).
Дисциплина изучается в 3,4 семестрах. В модуль входят следующие дисциплины:
Функциональный анализ (3 семестр), Обыкновенные дифференциальные уравнения. Теория
устойчивости (3,4 семестры), Теория функций комплексного переменного (3 семестр), Теория
вероятностей и математическая статистика (4 семестр), Введение в специальность (4 семестр).
Дисциплина направлена на изучение логического исчисления, теории графов,
комбинаторики, алгоритмов на графах и основ теории автоматов и является фундаментальной
основой для формирования математического мышления у будущих инженеров. Данный курс,
строясь на классических результатах, полученных в 18-20 веках, является основой для
формирования алгоритмического подхода у обучаемого при решении практических задач.
1.2. Язык реализации программы – русский
1.3. Планируемые результаты обучения по дисциплине
Результатом обучения в рамках дисциплины является формирование у студента
следующих компетенций:
ОПК-1 - готовность к самостоятельной работе;
ОПК-2 - способность использовать современные математические методы и современные
прикладные программные средства и осваивать современные технологии программирования;
ПК-9 - способность выявить естественнонаучную сущность проблем, возникающих в
ходе профессиональной деятельности, готовностью использовать для их решения
соответствующий естественнонаучный аппарат;
ПК-10 - готовность применять математический аппарат для решения поставленных задач,
способностью применить соответствующую процессу математическую модель и проверить ее
адекватность, провести анализ результатов моделирования, принять решение на основе
полученных результатов;
ПК-12 - способность самостоятельно изучать новые разделы фундаментальных наук;
В результате освоения дисциплины студент должен:
Знать:
1. Основные принципы перечисления объектов
2. Важнейшие системы чисел, появляющихся в комбинаторных подсчетах
3. Формулы включения-исключения
4. Методы решения рекуррентных соотношений
5. Основные понятия формальной логики
6. Элементарную теорию множеств (операции над множествами и основные факты, связанные
с понятием мощности множества)
7. Булеву логику высказываний (включая вопросы полноты систем булевых функций)
8. общую теорию формальных исчислений
9. Теоретико-множественную логику предикатов и ее взаимоотношения с (формальным)
исчислением предикатов
10. Основные характеристики графов
11. Специальные цепи и циклы в графах, понятия основного дерева в графе
12. Методы подсчета хроматического числа графа
13. Основные понятия теории алгоритмической сложности
59
60.
15. Основные понятия теории формальных языков и конечных автоматов.Уметь:
1. Применять математический аппарат при решении типовых задач, а также обнаруживать
применимость аппарата математической логики для решения задач из родственных областей
науки и ее приложений,
2. Строить производящие функции конкретных последовательностей и решать обратную
задачу
3. Решать простейшие рекуррентные соотношения
4. Решать практические задачи, связанные с построением конкретных комбинаторных
конфигураций и с подсчетом их количества
5. Находить количество решений целочисленных линейных уравнений в натуральных числах
6. Строить граф по его матрицам смежности или инциденций и решать обратную задачу
7. Строить циклы специального вида в графе
8. Находить хроматическое число и хроматический многочлен графа
9. Находить расстояния во взвешенном графе
10. Находить во взвешенном графе остов наименьшего веса
11. Находить максимальный поток в сети
12. Решать задачу о назначении.
Владеть (демонстрировать навыки и опыт деятельности):
1.Методами дискретной математики.
13.4.
Объем дисциплины
Очная форма обучения
Объем дисциплины
№
п/
п
Виды учебной работы
1.
2.
3.
4.
5.
6.
7.
8.
Распределение объема
дисциплины по семестрам (час.)
Всего
часов
В т.ч.
контактн
ая работа
(час.)*
3
4
Аудиторные занятия
Лекции
Практические занятия
Лабораторные работы
Самостоятельная работа студентов,
включая все виды текущей
аттестации
Промежуточная аттестация
119
51
68
119
51
68
51
17
34
68
34
34
147
17,85
89
58
22
2,58
Э,18
Общий объем по учебному плану,
час.
Общий объем по учебному плану,
з.е.
288
139,43
З,4
144
4
4
8
144
*Контактная работа составляет:
в п/п 2,3,4 - количество часов, равное объему соответствующего вида занятий;
в п.5 – количество часов, равное сумме объема времени, выделенного преподавателю на консультации в
группе (15% от объема аудиторных занятий) и объема времени, выделенного преподавателю на руководство
курсовой работой/проектом одного студента, если она предусмотрена.
в п.6 – количество часов, равное сумме объема времени, выделенного преподавателю на проведение
соответствующего вида промежуточной аттестации одного студента и объема времени, выделенного в рамках
дисциплины на руководство проектом по модулю (если он предусмотрен) одного студента.
60
61.
14. СОДЕРЖАНИЕ ДИСЦИПЛИНЫКод
раздела,
темы
Раздел, тема
дисциплины*
Содержание
Множества. Способы задания. Подмножества.
Пустое и универсальное множества. Операции.
Свойства операций. Разбиение. Декартово
произведение.
Р1
Логические исчисления
Р2
Комбинаторика
Р3
Теория графов
Р4
Алгоритмы на графах
Бинарные отношения. Свойства отношений.
Отношение эквивалентности. Фактор-множество.
Эквивалентность и разбиение. Отношение порядка.
Понятие о максимальном и наибольшем элементах.
Функции. Биекция и мощность множества. Понятие
булевой
функции.
Таблицы
истинности.
«Элементарные» булевы функции. Эквивалентность
формул. СДНФ. Логические задачи. Полиномы
Жегалкина. Теорема Поста. Частично определенные
булевы функции и их минимизация. Алгебра логики
высказываний. Тавтологии. Аксиомы и правила
вывода. Методы доказательств.
Правила суммы и произведения. Формула включений
и исключений. Размещения, перестановки и
сочетания. Биекция в комбинаторных задачах.
Задачи, приводящие к рекуррентным соотношениям.
Рекуррентные последовательности и производящие
функции. Восстановление линейной рекуррентной
последовательности по производящей функции.
Определения.
Способы
задания.
Леммы
о
рукопожатиях. Подграфы. Взвешенные графы.
Мультиграфы.
Маршруты, цепи, циклы, пути. Компоненты
связности. Сильная связность. Числа вершинной и
реберной связности. Эйлеровы циклы. Теорема
Эйлера.
Покрытие
графа
ребернонепересекающимися цепями. Деревья. Теорема об
эквивалентных определениях дерева. Остов. Сеть.
Поток. Разрез. Теорема Форда-Фалкерсона. Критерий
двудольности. Паросочетания. Укладка графа.
Плоские и планарные графы. Формула Эйлера.
Следствия. Теорема Понтрягина-Куратовского.
Понятие временной сложности. Свойства функции
сложности. Сводимость задач. Классы P и NP.
Сложность элементарных арифметических операций.
Поиск в ширину. Алгоритм Дейкстры. Алгоритм
Краскала. Алгоритм поиска компонент сильной
связности. Алгоритм поиска максимального потока в
сети. Алгоритм проверки наличия 2-раскраски.
61
62.
Р5Автоматы и языки
Венгерский алгоритм. Алгоритм поиска наибольшего
паросочетания минимального веса.
Определение.
Понятие
синхронизируемости.
Алгоритм
распознавания
синхронизируемых
автоматов. Языки. Грамматики. Иерархия Хомского.
Операции с языками. Автоматы распознаватели.
Эквивалентность распознавания ДКА, НКА и
конечным моноидом. Построение по НКА
эквивалентного
ДКА.
Построение
моноида
переходов.
Теорема
Клини.
Построение
рационального выражения по автомату. Построение
автомата по языку. Теорема Майхила-Нероуда.
Алгоритм минимизации ДКА.
15. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ
3.4. Распределение аудиторной нагрузки и мероприятий самостоятельной работы по
разделам дисциплины
Очная форма обучения
62
63.
Объем модуля (зач.ед.): 27 (УП № 5184),28 (УП № 6104)
Объем дисциплины ( зач.ед.): 8
Аудиторные
занятия (час.)
10
50
24
12
12
26
20
Алгоритмы на графах
46
20
10
10
26
18
Автоматы и языки
Всего (час), без учета
11
266
51
68
147
105
промежуточной
9
аттестации:
Всего по дисциплине
288
11
169
(час.):
9
*Суммарный объем в часах на мероприятие
указывается в строке «Всего (час.) без учета промежуточной аттестации
8
8
12
10
6
6
1
1
37
68
34
2
4
1
10
2
1
2
1
8
8
В т.ч. промежуточная аттестация
63
4
18
Подго
товка
в
рамка
х
дисци
плины
к
проме
жуточ
ной
аттест
ации
по
модул
ю
(час.)
Проект по модулю
12
Экзамен
8
1
1
Зачет
20
2
2
Коллоквиум*
32
Контрольная работа*
12
Всего (час.)
12
Теория графов
Курсовой проект*
24
Р3
Р4
Р5
Комбинаторика
Курсовая работа*
56
Р2
Перевод инояз. литературы*
1
1
Домашняя работа на иностр.
языке*
6
6
Расчетно-графическая работа*
16
18
Расчетная работа, разработка
программного продукта*
6
7
Проектная работа*
Домашняя работа*
22
25
Реферат, эссе, творч. работа*
Всего (час.)
30
33
Графическая работа*
Практ., семинар. занятие
16
18
Н/и семинар, семинар-конфер.,
коллоквиум (магистратура)
Лекция
8
9
Логические исчисления
Лабораторное занятие
Всего (час.)
24
27
Р1
Наименование раздела,
темы
Лабораторные работы
54
60
Код раздела, темы
Практические занятия
Выполнение самостоятельных внеаудиторных работ
(колич.)
Лекции
Подготовка к аудиторным
занятиям (час.)
Подготов
ка к
промежут
очной
аттестац
ии по
дисципли
не (час.)
Интегрированный экзамен по модулю
Подготовка к
контрольным
мероприятиям
текущей
аттестации
(колич.)
Всего аудиторной работы (час.)
Всего самостоятельной работы студентов (час.)
Самостоятельная работа: виды, количество и объемы мероприятий
Всего по разделу, теме (час.)
Раздел дисциплины
64.
16. ОРГАНИЗАЦИЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ, САМОСТОЯТЕЛЬНОЙ РАБОТЫПО ДИСЦИПЛИНЕ
6.7. Лабораторные работы
не предусмотрено
Код
раздела,
темы
6.8. Практические занятия
Номер
занятия
Р1
Р2
Р3
Р4
Р5
1
2
3
4
5
Время на
проведение
занятия (час.)
Тема занятия
Логические исчисления
Комбинаторика
Теория графов
Алгоритмы на графах
Автоматы и языки
Всего:
16
18
12
12
10
17
6. 4.3.Примерная тематика самостоятельной работы
4.3.10. Примерный перечень тем домашних работ
4. Логические исчисления
5. Комбинаторика
6. Графы
7. Автоматы и языки
4.3.11. Примерный перечень тем графических работ
не предусмотрено
4.3.12. Примерный перечень тем рефератов (эссе, творческих работ)
не предусмотрено
4.3.5 Примерная тематика индивидуальных или групповых проектов
не предусмотрено
4.3.15. Примерный перечень тем расчетных работ (программных продуктов)
Теория графов
4.3.16. Примерный перечень тем расчетно-графических работ
не предусмотрено
4.3.17. Примерный перечень тем курсовых проектов (курсовых работ)
не предусмотрено
16.4.1. Примерная тематика контрольных работ
4. Таблицы истинности
5. Комбинаторика
6. Графы
7. Автоматы и языки
4.3.9. Примерная тематика коллоквиумов
не предусмотрено
17. СООТНОШЕНИЕ РАЗДЕЛОВ, ТЕМ ДИСЦИПЛИНЫ И ПРИМЕНЯЕМЫХ
ТЕХНОЛОГИЙ ОБУЧЕНИЯ
Код раздела, темы
Активные методы обучения
64
Дистанционные
образовательные технологии и
65.
Р1-Р5Другие (указать, какие)
Вебинары и
видеоконференции
Асинхронные webконференции и семинары
Совместная работа и
разработка контента
Виртуальные практикумы
и тренажеры
Сетевые учебные курсы
Другие (указать, какие)
Командная работа
Проблемное обучение
Деловые игры
Кейс-анализ
электронное обучение
Проектная работа
дисциплины
*
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ
(Приложение 1)
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХ
НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ (Приложение 2)
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ (Приложение 3)
9. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ
ДИСЦИПЛИНЫ
9.1.Рекомендуемая литература
9.1.1.Основная литература
Макоха, А. Н. Дискретная математика / А.Н. Макоха ; П.А. Сахнюк ; Н.И. Червяков .—
Москва : Физматлит, 2005 .— 368 с. — ISBN 5-9221-0630-9 .—
<URL:http://biblioclub.ru/index.php?page=book&id=68366>.
Иванов, Б. Н. Дискретная математика : Алгоритмы и программы. Полный курс / Б.Н. Иванов
.— Москва : Физматлит, 2007 .— 407 с. — ISBN 978-5-9221-0787-7 .—
<URL:http://biblioclub.ru/index.php?page=book&id=75502>.
Редькин, Н. П. Дискретная математика / Н.П. Редькин .— Москва : Физматлит, 2009 .— 263 с.
— ISBN 978-5-9221-1093-8 .— <URL:http://biblioclub.ru/index.php?page=book&id=75709>.
9.1.2.Дополнительная литература
Кузнецов, Олег Петрович. Дискретная математика для инженера / О. П. Кузнецов .— 3-е
изд., перераб. и доп. — СПб. ; М. ; Краснодар : Лань, 2004 .— 400 с. : ил. ; 21 см .— (Учебники
для вузов, Специальная литература) .— Предм. указ.: с. 390-393. — Библиогр.: с. 388-389 (50
назв.). — ISBN 5-8114-0570-7.
Акимов, Олег Евгеньевич. Дискретная математика: логика, группы, графы / О.Е. Акимов .—
М. : Лаборатория Базовых Знаний, 2001 .— 352 с. : ил. ; 25 см .— (Технический университет)
.— без грифа .— ISBN 5-932080-53-1 : 97.20.
Асеев, Георгий Георгиевич. Дискретная математика : учеб. пособие / Г. Г. Асеев, О. М.
Абрамов, Д. Э. Ситников .— Ростов н/Д ; Харьков : Феникс : Торсинг, 2003 .— 144 с. : ил. ; 21
см .— (Учебники) .— Алф. указ.: с. 140-142. — Библиогр.: с. 138-139. — без грифа .— ISBN 5222-03775-4 .— ISBN 966-693-257-1.вузов, Специальная литература) .— Библиогр.: с. 96 (14
назв.). — ISBN 5-8114-0522-7.верситет, Математика) .— Библиогр.: с.285 (27 назв.) .— Предм.
указ.: с. 286-288. — ISBN 5-932080-93-0 : 90.00.
65
66.
9.2.Методические разработки1. Элементы дискретной математики: учебное пособие / Д.С. Ананичев, И.Ю. Андреева,
Н.В. Гредасова, К.В. Костоусов. – Екатеринбург: Изд-во Уральского университета,
2015. - 108 с.
9.3.Программное обеспечение
Не используется
9.4. Базы данных, информационно-справочные и поисковые системы
http://study.urfu.ru – портал информационно-образовательных ресурсов УрФУ
http://lib.urfu.ru – зональная научная библиотека УрФУ
http://poiskknig.ru – электронная библиотека учебников Мех-Мата МГУ, Москва
http://www.mathnet.ru. - общероссийский математический портал
http://onlinelibrary.wiley.com - научные журналы издательства Wiley&Sons
http://www.sciencedirect.com - научные журналы издательства Elsevier
https://www.coursera.org/ – массовые открытые онлайн-курсы;
https://www.edx.org/ – массовые открытые онлайн-курсы;
https://openedu.ru/ – национальная платформа открытого образования;
9.5.Электронные образовательные ресурсы
Не используется
10. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Сведения об оснащенности дисциплины специализированным и лабораторным
оборудованием
Мультимедийная аудитория Т-1208: 10 ПК, проектор; мультимедийная аудитория Т1202б: 10 ПК, проектор, интерактивная доска.
66
67.
ПРИЛОЖЕНИЕ 1к рабочей программе дисциплины
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В
РАМКАХ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
6.1. Весовой коэффициент значимости дисциплины –
6.2.Процедуры текущей и промежуточной аттестации по дисциплине
3 семестр
1.Лекции: коэффициент значимости совокупных результатов лекционных занятий – 0.6
Текущая аттестация на
Сроки –
Максималь
семестр,
ная оценка
учебная
в баллах
неделя
Экспертиза конспекта
3, 1-8
100
Весовой коэффициент значимости результатов текущей аттестации по лекциям – 0.4
Промежуточная аттестация по лекциям – зачет
Весовой коэффициент значимости результатов промежуточной аттестации по лекциям –
0.6.
2. Практические/семинарские занятия: коэффициент значимости совокупных
результатов практических/семинарских занятий – 0,4
Текущая аттестация на практических/семинарских
Сроки –
Максималь
занятиях
семестр,
ная оценка
учебная
в баллах
неделя
Домашняя работа 1
3,1-17
16
Домашняя работа 2
3,1-17
16
Контрольная работа 1
3,1-17
20
Контрольная работа 2
3,1-17
20
Работа на практических занятиях
3,1-17
28
Весовой коэффициент значимости результатов текущей аттестации по
практическим/семинарским занятиям– 1.0
Промежуточная аттестация по практическим/семинарским занятиям– не предусмотрено
Весовой коэффициент значимости результатов промежуточной аттестации по
практическим/семинарским занятиям– 0.0
3. Лабораторные занятия: коэффициент значимости совокупных результатов
лабораторных занятий –0.0
Весовой коэффициент значимости результатов текущей аттестации по лабораторным
занятиям -0.0
Промежуточная аттестация по лабораторным занятиям– не предусмотрено
Весовой коэффициент значимости результатов промежуточной аттестации по
лабораторным занятиям– 0.0
4 семестр
1.Лекции: коэффициент значимости совокупных результатов лекционных занятий – 0.6
Текущая аттестация на
Сроки –
Максималь
семестр,
ная оценка
учебная
в баллах
неделя
Экспертиза конспекта
3, 1-17
100
Весовой коэффициент значимости результатов текущей аттестации по лекциям – 0.4
Промежуточная аттестация по лекциям – экзамен
Весовой коэффициент значимости результатов промежуточной аттестации по лекциям –
67
68.
0.6.2. Практические/семинарские занятия: коэффициент значимости совокупных
результатов практических/семинарских занятий – 0,4
Текущая аттестация на практических/семинарских
Сроки –
Максималь
занятиях
семестр,
ная оценка
учебная
в баллах
неделя
Домашняя работа 1
3,1-17
10
Домашняя работа 2
3,1-17
10
Контрольная работа 1
3,1-17
18
Контрольная работа 2
3,1-17
18
Расчетная работа
3,1-17
16
Работа на практических занятиях
3,1-17
28
Весовой коэффициент значимости результатов текущей аттестации по
практическим/семинарским занятиям– 1.0
Промежуточная аттестация по практическим/семинарским занятиям– не предусмотрено
Весовой коэффициент значимости результатов промежуточной аттестации по
практическим/семинарским занятиям– 0.0
3. Лабораторные занятия: коэффициент значимости совокупных результатов
лабораторных занятий –0.0
Весовой коэффициент значимости результатов текущей аттестации по лабораторным
занятиям -0.0
Промежуточная аттестация по лабораторным занятиям– не предусмотрено
Весовой коэффициент значимости результатов промежуточной аттестации по
лабораторным занятиям– 0.0
6.3. Процедуры текущей и промежуточной аттестации курсовой работы/проекта
Весовой коэффициент текущей аттестации выполнения курсовой работы/проекта 0.0
Весовой коэффициент промежуточной аттестации выполнения курсовой
работы/проекта– защиты – 0.0
6.4. Коэффициент значимости семестровых результатов освоения дисциплины
Порядковый номер семестра по учебному
Коэффициент значимости результатов
плану, в котором осваивается дисциплина
освоения дисциплины в семестре
0,4
Семестр 3
0,6
Семестр 4
*В случае проведения промежуточной аттестации по дисциплине (экзамена, зачета) методом
тестирования используются официально утвержденные ресурсы: АПИМ УрФУ, СКУД УрФУ,
имеющие статус ЭОР УрФУ; ФЭПО (www.фэпо.рф); Интернет-тренажеры (www.i-exam.ru).
68
69.
ПРИЛОЖЕНИЕ 2к рабочей программе дисциплины
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХ
НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
сайте ФЭПО http://fepo.i-exam.ru.
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
сайте Интернет-тренажеры http://training.i-exam.ru.
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
портале СМУДС УрФУ.
В связи с отсутствием Дисциплины и ее аналогов, по которым возможно
тестирование, на сайтах ФЭПО, Интернет-тренажеры и портале СМУДС УрФУ,
тестирование в рамках НТК не проводится.
69
70.
ПРИЛОЖЕНИЕ 3к рабочей программе дисциплины
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
8.1. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ КОНТРОЛЬНО-ОЦЕНОЧНЫХ
МЕРОПРИЯТИЙ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО
ДИСЦИПЛИНЕ В РАМКАХ БРС
В рамках БРС применяются утвержденные на кафедре критерии оценивания
достижений студентов по каждому контрольно-оценочному мероприятию. Система критериев
оценивания, как и при проведении промежуточной аттестации по модулю, опирается на три
уровня освоения компонентов компетенций: пороговый, повышенный, высокий.
Компоненты
Признаки уровня освоения компонентов компетенций
компетенций
пороговый
повышенный
высокий
Студент демонстрирует
Студент демонстрирует Студент может
Знания
знание-знакомство,
аналитические знания:
самостоятельно
знание-копию: узнает
уверенно воспроизводит извлекать новые знания
объекты, явления и
и понимает полученные из окружающего мира,
понятия, находит в них
знания, относит их к той творчески их
различия, проявляет
или иной
использовать для
знание источников
классификационной
принятия решений в
получения информации,
группе, самостоятельно новых и нестандартных
может осуществлять
систематизирует их,
ситуациях.
самостоятельно
устанавливает
репродуктивные действия взаимосвязи между
над знаниями путем
ними, продуктивно
самостоятельного
применяет в знакомых
воспроизведения и
ситуациях.
применения информации.
Студент умеет корректно
Студент умеет
Студент умеет
Умения
выполнять предписанные самостоятельно
самостоятельно
действия по инструкции,
выполнять действия
выполнять действия,
алгоритму в известной
(приемы, операции) по
связанные с решением
ситуации, самостоятельно решению нестандартных исследовательских
выполняет действия по
задач, требующих
задач, демонстрирует
решению типовых задач,
выбора на основе
творческое
требующих выбора из
комбинации известных использование умений
числа известных методов, методов, в
(технологий)
в предсказуемо
непредсказуемо
изменяющейся ситуации
изменяющейся ситуации
Студент имеет
Студент имеет
Личностные Студент имеет низкую
мотивацию учебной
выраженную мотивацию развитую мотивацию
качества
деятельности, проявляет
учебной деятельности,
учебной и трудовой
безразличное,
демонстрирует
деятельности,
безответственное
позитивное отношение к проявляет
отношение к учебе,
обучению и будущей
настойчивость и
порученному делу
трудовой деятельности, увлеченность,
проявляет активность.
трудолюбие,
самостоятельность,
творческий подход.
70
71.
8.2. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИПРИ ИСПОЛЬЗОВАНИИ НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ
При проведении независимого тестового контроля как формы промежуточной
аттестации применяется методика оценивания результатов, предлагаемая разработчиками
тестов. Процентные показатели результатов независимого тестового контроля переводятся в
баллы промежуточной аттестации по 100-балльной шкале в БРС:
в случае балльной оценки по тесту (блокам, частям теста) переводится процент набранных
баллов от общего числа возможных баллов по тесту;
при отсутствии балльной оценки по тесту переводится процент верно выполненных
заданий теста, от общего числа заданий.
8.3. ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ
И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
8.3.1. Примерные задания для проведения домашних работ
3 семестр
Домашняя работа № 1
1. Приведите примеры бинарных отношений:
а) транзитивных и симметричных, но нерефлексивных;
б) рефлексивных и транзитивных, но несимметричных.
2. Построить таблицу истинности для булевой функции, заданной логической формулой
f ( X , Y , Z ) ( X Y Z ) & (Z Y ) . Произвести разложение функции по переменной X.
Домашняя работа № 2
1. Сколько существует 6-значных чисел, все цифры которых имеют одинаковую
четность?
2. На полке стоят 5 книг. Сколькими способами можно выложить в стопку несколько из
них (стопка может состоять и из одной книги)?
3. Сколько слов можно составить из 5 букв А и не более, чем из трех букв Б?
4 семестр
Домашняя работа № 1
Используйте алгоритм Дейкстры для нахождения в приведенных ниже графах кратчайшего
расстояния между вершинами v0 и v.
71
72.
Домашняя работа № 2По словесному описанию языка составить регулярное выражение. Составить грамматику,
порождающую данный язык и выписать вывод какого-нибудь четырехбуквенного или
пятибуквенного слова. Длина каждого слова не меньше 2, и вторая буква всегда b.
8.3.2. Примерные задания для проведения расчетной работы
Задание 1.
Какие пары графов, изображенные на рисунке изоморфны?
Задание 2.
1. Найдите остовные деревья в графах K5, K3,3.
2. Построить все неизоморфные трех, четырех - и пятивершинные деревья.
3. Докажите, что каждое ребро в дереве – мост.
8.3.3. Примерные контрольные задачи в рамках учебных занятий
3 семестр
Контрольная работа № 1
1. Приведите пример множеств А, В, С таких, чтобы выполнялись условия:
а) A B, A C, C B ;
б) A B, B C, A C .
2. Докажите следующие утверждения:
а) A B B C A C ;
72
73.
б) A B B C A C .Контрольная работа № 2
1. Сколько различных слов можно получить, переставляя буквы слова «БИССЕКТРИСА»,
предполагая, что словом является любая конечная последовательность русского
алфавита.
2. Сколько диагоналей в выпуклом n-угольнике?
4 семестр
Контрольная работа № 1
1. При каких значениях n граф Kn является двудольным?
2. Является ли граф, изображенный на рисунке двудольным?
Контрольная работа № 2
По заданной грамматике составить источник; детерминировать его; получить автомат,
представляющий тот же язык, минимизировать полученный автомат; записать грамматику для
минимального автомата.
8.3.4. Примерные контрольные кейсы
не предусмотрено
8.3.5. Перечень примерных вопросов для зачета
1. Множества. Способы задания. Подмножества. Пустое и универсальное множества.
2. Операции. Свойства операций. Разбиение. Декартово произведение.
3. Бинарные отношения.
4. Свойства отношений. Отношение эквивалентности.
5. Фактор-множество. Эквивалентность и разбиение.
6. Отношение порядка. Понятие о максимальном и наибольшем элементах.
7. Функции. Биекция и мощность множества.
8. Понятие булевой функции. Таблицы истинности.
9. «Элементарные» булевы функции. Эквивалентность формул. СДНФ.
10. Логические задачи. Полиномы Жегалкина.
11. Теорема Поста. Частично определенные булевы функции и их минимизация.
12. Алгебра логики высказываний.
13. Тавтологии.
14. Аксиомы и правила вывода.
15. Методы доказательств.
16. Правила суммы и произведения.
17. Формула включений и исключений.
18. Размещения, перестановки и сочетания.
19. Биекция в комбинаторных задачах.
20. Задачи, приводящие к рекуррентным соотношениям.
21. Рекуррентные последовательности и производящие функции.
22. Восстановление линейной рекуррентной последовательности по производящей
функции.
8.3.6. Перечень примерных вопросов для экзамена
73
74.
1. Способы задания. Леммы о рукопожатиях. Подграфы. Взвешенные графы.Мультиграфы.
2. Маршруты, цепи, циклы, пути.
3. Компоненты связности. Сильная связность.
4. Числа вершинной и реберной связности.
5. Эйлеровы циклы. Теорема Эйлера.
6. Покрытие графа реберно-непересекающимися цепями.
7. Деревья. Теорема об эквивалентных определениях дерева.
8. Остов. Сеть. Поток. Разрез.
9. Теорема Форда-Фалкерсона.
10. Критерий двудольности.
11. Паросочетания. Укладка графа.
12. Плоские и планарные графы.
13. Теорема Понтрягина-Куратовского.
14. Понятие временной сложности. Свойства функции сложности.
15. Сводимость задач. Классы P и NP.
16. Сложность элементарных арифметических операций. Поиск в ширину.
17. Алгоритм Дейкстры.
18. Алгоритм Краскала.
19. Алгоритм поиска компонент сильной связности.
20. Алгоритм поиска максимального потока в сети.
21. Алгоритм проверки наличия 2-раскраски.
22. Венгерский алгоритм.
23. Алгоритм поиска наибольшего паросочетания минимального веса.
24. Понятие синхронизируемости.
25. Алгоритм распознавания синхронизируемых автоматов.
26. Языки. Грамматики. Иерархия Хомского. Операции с языками.
27. Автоматы распознаватели. Эквивалентность распознавания ДКА, НКА и конечным
моноидом. Построение по НКА эквивалентного ДКА.
28. Построение моноида переходов.
29. Теорема Клини. Построение рационального выражения по автомату.
30. Построение автомата по языку.
31. Теорема Майхила-Нероуда.
32. Алгоритм минимизации ДКА.
8.3.7. Ресурсы АПИМ УрФУ, СКУД УрФУ для проведения тестового контроля в рамках
текущей и промежуточной аттестации
не используются
8.3.8. Ресурсы ФЭПО для проведения независимого тестового контроля
не используются
8.3.9. Интернет-тренажеры
не используются
74
75.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное автономное образовательное учреждение
высшего образования
«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
ВВЕДЕНИЕ В СПЕЦИАЛЬНОСТЬ
Перечень сведений о рабочей программе
дисциплины
Модуль Специальные главы математика
Учетные данные
Код модуля 1127561
Учебный план в ЕИСУ № 6104
Код ОП
01.03.04/01.01
Код направления и уровня
подготовки.
01.03.04
Образовательная программа
Прикладная математика
Направление подготовки
Прикладная математика
Уровень подготовки
Бакалавриат
ФГОС ВО
Реквизиты приказа Минобрнауки
РФ об утверждении ФГОС ВО:
12 марта 2015 г., № 208
Екатеринбург, 2017
75
76.
Рабочая программа дисциплины составлена авторами:№ п/п
ФИО
1
Сесекин Александр
Николаевич
Ученая степень,
ученое звание
Д.ф.-м.н.,
профессор
Руководитель модуля
Должность
Профессор
Кафедра
Подпись
Прикладн
ая
математи
ка
А.Н. Сесекин
Рекомендовано учебно-методическим советом Уральского энергетического института
Председатель учебно-методического совета
Протокол № ______ от __________ г.
Е.В. Черепанова
Согласовано:
Дирекция образовательных программ
Р.Х. Токарева
76
77.
5. ОБЩАЯ ХАРАКТЕРИСТИКА ДИСЦИПЛИНЫ «ВВЕДЕНИЕ ВСПЕЦИАЛЬНОСТЬ»
1.5.Аннотация содержания дисциплины
Дисциплина относится к модулю «Специальные главы математики» (базовая часть).
Дисциплина изучается 4 семестре. В модуль входят следующие дисциплины:
Функциональный анализ (3 семестр), Обыкновенные дифференциальные уравнения и теория
устойчивости (3,4 семестры), Теория функций комплексного переменного и операционное
исчисление (3 семестр), Теория вероятностей и математическая статистика (4 семестр),
Введение в специальность (4 семестр), Дискретная математика (3,4 семестр).
Данная дисциплина посвящена ознакомлению студентов с местом математики в
современном мире, задачам, решаемым специалистами по прикладной математике, задачам
учебного плана направления «Прикладная математика». А также обсуждаются рад
исторических аспектов развития математики. Будут рассмотрены вопросы, связанные с
развитием прикладной математики на Урале. Отдельный раздел программы посвящен
издательской системе для математических текстов LaTeX. В результате студенты овладеют
навыками работы в издательской системе LaTeX.
1.2. Язык реализации программы – русский.
1.3. Планируемые результаты обучения по дисциплине
Результатом освоения дисциплины является формирование у студента следующих
компетенций:
ОПК1. Готовностью к самостоятельной работе (ОПК-1).
ОПК2. Способностью использовать современные математические методы и современные
прикладные программные средства и осваивать современные технологии программирования
(ОПК-2).
ПК9. Способностью выявить естественнонаучную сущность проблем, возникающих в ходе
профессиональной деятельности, готовностью использовать для их решения соответствующий
естественнонаучный аппарат (ПК-9).
ПК10. Готовностью применять математический аппарат для решения поставленных задач,
способностью применить соответствующую процессу математическую модель и проверить ее
адекватность (ПК-10).
ПК12. Способностью самостоятельно изучать новые разделы фундаментальных наук (ПК-12).
В результате освоения дисциплины студент должен:
Знать:
основные направления развития прикладной математики;
основные задачи учебного плана специальности;
историю развития прикладной математики в мире, в стране, на Урале.
основы издательской системы LaTeX.
Уметь:
самостоятельно находить и работать с первоисточниками;
создавать математические тексты с помощью издательской системы LaTeX
Владеть (демонстрировать навыки и опыт деятельности):
навыками создания и оформления математических знаний в виде математических текстов
17.4.
Объем дисциплины
77
78.
Объем дисциплины№
п/
п
Виды учебной работы
1.
2.
3.
4.
5.
6.
7.
8.
Распределение объема
дисциплины по семестрам (час.)
Всего
часов
В т.ч.
контактн
ая работа
(час.)*
4
Аудиторные занятия
Лекции
Практические занятия
Лабораторные работы
Самостоятельная работа студентов,
включая все виды текущей
аттестации
Промежуточная аттестация
34
17
17
34
17
17
34
17
17
70
5,10
70
4
0,25
З, 4
Общий объем по учебному плану,
час.
Общий объем по учебному плану,
з.е.
108
39,35
108
3
3
*Контактная работа составляет:
в п/п 2,3,4 - количество часов, равное объему соответствующего вида занятий;
в п.5 – количество часов, равное сумме объема времени, выделенного преподавателю на консультации в
группе (15% от объема аудиторных занятий) и объема времени, выделенного преподавателю на руководство
курсовой работой/проектом одного студента, если она предусмотрена.
в п.6 – количество часов, равное сумме объема времени, выделенного преподавателю на проведение
соответствующего вида промежуточной аттестации одного студента и объема времени, выделенного в рамках
дисциплины на руководство проектом по модулю (если он предусмотрен) одного студента.
18. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
Код
раздела,
темы
Р1
Раздел, тема
дисциплины*
Содержание
Специальность «Прикладная Абстрактная и прикладная математика. Математика
математика»
и другие естественные науки. Эксперимент и
математические методы. Роль вычислительной
техники в математических исследованиях.
Математическая
модель,
ее
адекватность
изучаемому явлению или объекту. Критерий
практики. Развитие и уточнение математической
модели.
Вычислительные
алгоритмы.
Вычислительный
эксперимент
как
метод
исследования.
Математические
модели
в
естествознании,
теплоэнергетике,
медицине,
экономике, гуманитарных науках..
на Демонстрация документального фильма
«Устойчивость движения» об истории становления
математической науки на Урале и о ее сегодняшнем
дне.
Р2
Математическое
моделирование
Р3
Развитие
Урале
Р4
Издательская система LaTeX
математики
Основные понятия LaTeXa, набот формул в LaTeXе,
рисунки в LaTeXе. Создание макета печатного издания.
78
79.
19. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ3.5. Распределение аудиторной нагрузки и мероприятий самостоятельной работы по
разделам дисциплины
79
80.
Объем модуля: 28 (зач.ед.)Объем дисциплины: 2 (зач.ед.)
Аудиторные
занятия (час.)
4
4
2
2
80
22
11
11
58
22
11
11
17
17
Всего (час), без учета
104
34
17
17 0 70
34
промежуточной аттестации:
Всего по дисциплине
108
34
34
(час.):
*Суммарный объем в часах на мероприятие
указывается в строке «Всего (час.) без учета промежуточной аттестации
36
0
0
36
0
0
0
0
0
0
0
4
0
0
0
2
0
0
0
0
0
2
В т.ч. промежуточная аттестация
80
Проект по модулю
2
Интегрированный экзамен по модулю
2
Подгот
овка в
рамках
дисцип
лины к
проме
жуточн
ой
аттест
ации
по
модул
ю
(час.)
Экзамен
4
Подготов
ка к
промежут
очной
аттестац
ии по
дисципли
не (час.)
Зачет
8
Коллоквиум*
2
Контрольная работа*
2
Всего (час.)
4
Курсовой проект*
4
Курсовая работа*
2
Перевод инояз. литературы*
2
Домашняя работа на иностр.
языке*
4
Расчетно-графическая работа*
8
Расчетная работа, разработка
программного продукта*
2
Проектная работа*
2
Реферат, эссе, творч. работа*
4
Графическая работа*
4
Домашняя работа*
2
Выполнение самостоятельных внеаудиторных работ (колич.)
Всего (час.)
2
Н/и семинар, семинар-конфер.,
коллоквиум (магистратура)
Практ., семинар. занятие
4
Лабораторное занятие
Лекция
Всего самостоятельной работы студентов (час.)
8
Лабораторные работы
Всего (час.)
Р4
Практические занятия
Р3
Подготовка к
аудиторным занятиям
(час.)
Лекции
Р2
Специальность
«Прикладная математика»
Математическое
моделирование
Развитие математики на
Урале
Издательская система
LaTeX.
Подготовка к
контрольным
мероприятиям
текущей
аттестации (колич.)
Всего аудиторной работы (час.)
Р1
Наименование раздела,
темы
Самостоятельная работа: виды, количество и объемы мероприятий
Всего по разделу, теме (час.)
Код раздела, темы
Раздел дисциплины
81.
20. ОРГАНИЗАЦИЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ, САМОСТОЯТЕЛЬНОЙ РАБОТЫПО ДИСЦИПЛИНЕ
6.9. Лабораторные работы
Не предусмотрено.
Код
раздела,
темы
6.10.
Р1
Р2
Р3
Р4
Практические занятия
Номер
занятия
1
2
3
4-17
Время на
проведение
занятия (час.)
Тема занятия
Специальность «Прикладная математика»
Математическое моделирование.
Развитие математики на Урале..
Издательская система LaTeX.
Всего:
2
2
2
11
17
7. 4.3.Примерная тематика самостоятельной работы
4.3.13. Примерный перечень тем домашних работ
Не предусмотрено.
4.3.14. Примерный перечень тем графических работ
Не предусмотрено.
4.3.15. Примерный перечень тем рефератов (эссе, творческих работ)
Не предусмотрено.
4.3.4 Примерная тематика индивидуальных или групповых проектов
Не предусмотрено.
4.3.18. Примерный перечень тем расчетных работ (программных продуктов)
Не предусмотрено.
4.3.19. Примерный перечень тем расчетно-графических работ
Создание макета математического издания.
Создание макета презентации лекции.
4.3.20. Примерный перечень тем курсовых проектов (курсовых работ)
Не предусмотрено.
4.3.21. Примерная тематика контрольных работ
Не предусмотрено.
4.3.9. Примерная тематика коллоквиумов
Не предусмотрено.
21. СООТНОШЕНИЕ РАЗДЕЛОВ, ТЕМ ДИСЦИПЛИНЫ И ПРИМЕНЯЕМЫХ
ТЕХНОЛОГИЙ ОБУЧЕНИЯ
Код раздела, темы
дисциплины
Активные методы обучения
81
Дистанционные
образовательные технологии и
электронное обучение
82.
Другие (указать, какие)Вебинары и
видеоконференции
Асинхронные webконференции и семинары
Совместная работа и
разработка контента
Виртуальные практикумы
и тренажеры
Сетевые учебные курсы
Другие (указать, какие)
Командная работа
Проблемное обучение
Деловые игры
Кейс-анализ
Проектная работа
Р1-Р4
*
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ
(Приложение 1)
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХ
НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ (Приложение 2)
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ (Приложение 3)
9. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ
ДИСЦИПЛИНЫ
9.1.Рекомендуемая литература
9.1.1.Основная литература
1. Блехман И.И. Прикладная математика: предмет, логика, особенности подходов. С
примерами из механики : [учебное пособие] / И. И. Блехман, А. Д. Мышкис, Я. Г.
Пановко .— [Изд. 3-е, испр. и доп.] .— Москва : [КомКнига], 2005 .— 376 c. (ЗНБ
УрФУ).
2. Охорзин В.А. Прикладная математика в системе Mathcad : учеб. пособие для студентов
вузов, обучающихся по направлению подгот. дипломир. специалиста 160400 "Системы упр. движением и навигации" и специальности 160403 - "Системы упр.
летательными аппаратами" / В. А. Охорзин .— 2-е изд., испр. и доп. — СанктПетербург ; Москва ; Краснодар : Лань, 2008 .— 352 с. (ЗНБ УрФУ).
3. Панов В.Ф. Математика древняя и юная / В.Ф. Панов. М.: Изд-во МГТУ им. Н.Э.
Баумана, 2006г. (ЗНБ УрФУ).
4. Львовский С.М. Набор и верстка в пакете LaTeX. М.: КОСМОСИНФОРМ.
1995.374 с. (ЗНБ УрФУ
9.1.2.Дополнительная литература
1. Гиндикин Г.М. Рассказы о физиках и математиках / С. Г. Гиндикин .— М. : Наука,
Гл. ред. физ.-мат. лит., 1981 .— 189 с. (ЗНБ УрФУ).
2. Клейн Ф. Лекции о развитии математики в XIX столетии / Ф. Клейн.: В 2 т.: Пер. с
нем. Т. 1 .— М. : Наука, 1989 .— 453 с. : . (ЗНБ УрФУ).
3. Курант Р. Что такое математика? / Р. Курант, Г. Роббинс. М.: МЦНМО. 2000г. .
(ЗНБ УрФУ).
4. Реньи .Диалоги по математике / пер. с англ. Д. Б. Гнеденко, Е. А. Масловой; под
ред. и с предисл. акад. Б. В. Гнеденко .— М. : Мир, 1969 .— 96.. . (ЗНБ УрФУ).
5. Гнеденко Б.В. Очерки по истории математики в России. М.: УРСС. 2005. 292 с.
6. Тихонов А.Н. Вводные лекции по прикладной математике / А.Н. Тихонов, Д.П.
Костомаров Д.П. - М.:Наука., 1984г. . (ЗНБ УрФУ).
82
83.
7. Моисеев Н.Н. Математика ставит эксперимент. / Н.Н. Моисеев М.: Наука, 1979г. .(ЗНБ УрФУ).
8. Говорухин В. Компьютер в математическом исследовании: Maple, MATLAB,
LaTeX: Учеб. курс / В. Говорухин, В. Цибулин .— СПб.; М.; Харьков; Минск :
Питер, 2001 .— 624 с. : ил. ; 23 см .— (Учебный курс) .— Библиогр.: с. 598-601 (81
назв.). - Алф. указ.: с. 602-619. (ЗНБ УрФУ).
9. Грэтцер Г. Первые шаги в LaTEX'е / Г. Грэтцер ; Пер. с англ. И. А. Маховой .— М.
: Мир, 2000 .— 172 с.
9.2.Методические разработки
Не используются
9.3.Программное обеспечение
Издательская система LaTeX.
9.4. Базы данных, информационно-справочные и поисковые системы
http://poiskknig.ru – электронная библиотека учебников Мех-Мата МГУ, Москва
http://www.mathnet.ru. - общероссийский математический портал
http://onlinelibrary.wiley.com - научные журналы издательства Wiley&Sons
http://www.sciencedirect.com - научные журналы издательства Elsevier
http://lib.urfu.ru – зональная научная библиотека УрФУ
9.5.Электронные образовательные ресурсы
Портал информационно - образовательных ресурсов УрФУ http://study.ustu.ru
10. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Сведения об оснащенности дисциплины специализированным и лабораторным
оборудованием
Учебный, лекционный класс (Т-1202):
Проектор, экран.
Компьютерный класс (Т-1208):
Компьютеры – 12 шт., объединены в локальную сеть с выходом в Интернет.
Мультимедийное оборудование (мультимедийный проектор, экран).
83
84.
ПРИЛОЖЕНИЕ 1к рабочей программе дисциплины
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В
РАМКАХ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
6.1. Весовой коэффициент значимости дисциплины –
6.2.Процедуры текущей и промежуточной аттестации по дисциплине –
1.Лекции: коэффициент значимости совокупных результатов лекционных занятий – 0,6…
Текущая аттестация на
Сроки –
Максималь
семестр,
ная оценка
учебная
в баллах
неделя
Экспертиза конспектов
3, 1-9
100
Весовой коэффициент значимости результатов текущей аттестации по лекциям – 0,4
Промежуточная аттестация по лекциям – зачет
Весовой коэффициент значимости результатов промежуточной аттестации по лекциям –
0,6
2. Практические/семинарские занятия: коэффициент значимости совокупных
результатов практических/семинарских занятий – 0,4
Текущая аттестация на практических/семинарских
Сроки –
Максималь
занятиях
семестр,
ная оценка
учебная
в баллах
неделя
Расчетно-графическая работа 1
3, 10-17
30
Расчетно-графическая работа 2
3, 10-17
30
Работа на практических занятиях
3, 10-17
40
Весовой коэффициент значимости результатов текущей аттестации по
практическим/семинарским занятиям– 1
Промежуточная аттестация по практическим/семинарским занятиям– (не предусмотрено)
Весовой коэффициент значимости результатов промежуточной аттестации по
практическим/семинарским занятиям– 0
3. Лабораторные занятия: коэффициент значимости совокупных результатов
лабораторных занятий – не предусмотрено
6.3. Процедуры текущей и промежуточной аттестации курсовой работы/проекта
Не предусмотрено
6.4. Коэффициент значимости семестровых результатов освоения дисциплины
Порядковый номер семестра по учебному
Коэффициент значимости результатов
плану, в котором осваивается дисциплина
освоения дисциплины в семестре
Семестр 3
1
*В случае проведения промежуточной аттестации по дисциплине (экзамена, зачета) методом
тестирования используются официально утвержденные ресурсы: АПИМ УрФУ, СКУД УрФУ,
имеющие статус ЭОР УрФУ; ФЭПО (www.фэпо.рф); Интернет-тренажеры (www.i-exam.ru).
84
85.
ПРИЛОЖЕНИЕ 2к рабочей программе дисциплины
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХ
НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
сайте ФЭПО http://fepo.i-exam.ru.
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
сайте Интернет-тренажеры http://training.i-exam.ru.
Дисциплина и ее аналоги, по которым возможно тестирование, отсутствуют на
портале СМУДС УрФУ.
В связи с отсутствием Дисциплины и ее аналогов, по которым возможно
тестирование, на сайтах ФЭПО, Интернет-тренажеры и портале СМУДС УрФУ,
тестирование в рамках НТК не проводится.
85
86.
ПРИЛОЖЕНИЕ 3к рабочей программе дисциплины
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
8.1. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ КОНТРОЛЬНО-ОЦЕНОЧНЫХ
МЕРОПРИЯТИЙ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО
ДИСЦИПЛИНЕ В РАМКАХ БРС
В рамках БРС применяются утвержденные на кафедре критерии оценивания
достижений студентов по каждому контрольно-оценочному мероприятию. Система критериев
оценивания, как и при проведении промежуточной аттестации по модулю, опирается на три
уровня освоения компонентов компетенций: пороговый, повышенный, высокий.
Компоненты
Признаки уровня освоения компонентов компетенций
компетенций
пороговый
повышенный
высокий
Студент демонстрирует
Студент демонстрирует Студент может
Знания
знание-знакомство,
аналитические знания:
самостоятельно
знание-копию: узнает
уверенно воспроизводит извлекать новые знания
объекты, явления и
и понимает полученные из окружающего мира,
понятия, находит в них
знания, относит их к той творчески их
различия, проявляет
или иной
использовать для
знание источников
классификационной
принятия решений в
получения информации,
группе, самостоятельно новых и нестандартных
может осуществлять
систематизирует их,
ситуациях.
самостоятельно
устанавливает
репродуктивные действия взаимосвязи между
над знаниями путем
ними, продуктивно
самостоятельного
применяет в знакомых
воспроизведения и
ситуациях.
применения информации.
Студент умеет корректно
Студент умеет
Студент умеет
Умения
выполнять предписанные самостоятельно
самостоятельно
действия по инструкции,
выполнять действия
выполнять действия,
алгоритму в известной
(приемы, операции) по
связанные с решением
ситуации, самостоятельно решению нестандартных исследовательских
выполняет действия по
задач, требующих
задач, демонстрирует
решению типовых задач,
выбора на основе
творческое
требующих выбора из
комбинации известных использование умений
числа известных методов, методов, в
(технологий)
в предсказуемо
непредсказуемо
изменяющейся ситуации
изменяющейся ситуации
Студент имеет
Студент имеет
Личностные Студент имеет низкую
мотивацию учебной
выраженную мотивацию развитую мотивацию
качества
деятельности, проявляет
учебной деятельности,
учебной и трудовой
безразличное,
демонстрирует
деятельности,
безответственное
позитивное отношение к проявляет
отношение к учебе,
обучению и будущей
настойчивость и
порученному делу
трудовой деятельности, увлеченность,
проявляет активность.
трудолюбие,
самостоятельность,
творческий подход.
86
87.
8.2. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИПРИ ИСПОЛЬЗОВАНИИ НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ
При проведении независимого тестового контроля как формы промежуточной
аттестации применяется методика оценивания результатов, предлагаемая разработчиками
тестов. Процентные показатели результатов независимого тестового контроля переводятся в
баллы промежуточной аттестации по 100-балльной шкале в БРС:
в случае балльной оценки по тесту (блокам, частям теста) переводится процент набранных
баллов от общего числа возможных баллов по тесту;
при отсутствии балльной оценки по тесту переводится процент верно выполненных
заданий теста, от общего числа заданий.
8.3. ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ
И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
8.3.1. Примерные задания для расчетно-графических работ
Расчетно-графическая работа № 1
Создание математических формул в издательской системе LaTEX.
Запрограммировать формулу:
c l 0 (t* )
, t [t* , t* j );
j
U (t ) j || l 0 (t* ) ||
0,
t [t 0 , ] \ [t* , t* j ).
Расчетно-графическая работа № 2
Создание блоков для текстовых фрагментов презентаций и формул с помощью beamer.
8.3.2. Примерные контрольные задачи в рамках учебных занятий
Не предусмотрено
8.3.3. Примерные контрольные кейсы
Не предусмотрено
8.3.4. Перечень примерных вопросов для зачета
1. Основные документы, определяющие содержание подготовки студента.
(перечислить; указать, кем утверждается; какую информацию содержит).
2. Каковы основные области деятельности выпускника направления «Прикладная
математика»? (Указать объекты профессиональной деятельности, возможные места
работы и др.)
3. Охарактеризовать предметы гуманитарного и социально-экономического цикла. Зачем
нужно их изучать?
4. Охарактеризовать предметы математического и естественнонаучного цикла. Зачем
нужно их изучать?
5. Охарактеризовать предметы профессионального цикла. Зачем нужно их изучать?
6. Описать курсы по математическому моделированию. Охарактеризовать подробнее
одну-две дисциплины.
7. Рассказать об основных оптимизационных задачах.
8. Что такое «информационная система» и «информационная технология»?
9. Какие курсы (разделы курсов) посвящены изучению информационных систем?
10. Какие курсы (разделы курсов) посвящены изучению языков программирования? О чем
они?
11. Что изучают в курсах (разделах курсов) по проектированию информационных систем?
12. Что такое техническое обеспечение информационных систем и технологий? Дайте
развернутый ответ.
87
88.
13. Издательская система LaTeX. Стили.14. Набор формул в LaTeXе.
15. Создание рисунков в LaTeXе.
16. Таблицы в LaTeXе.
.
8.3.5. Перечень примерных вопросов для экзамена
Не предусмотрено.
8.3.6. Ресурсы АПИМ УрФУ, СКУД УрФУ для проведения тестового контроля в рамках
текущей и промежуточной аттестации
не используются
8.3.7. Ресурсы ФЭПО для проведения независимого тестового контроля
не используются
8.3.8. Интернет-тренажеры
не используются
88
89.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное автономное образовательное учреждение
высшего образования
«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Перечень сведений о рабочей программе
дисциплины
Модуль
Специальные главы математики
Образовательная программа
Прикладная математика
Направление подготовки
Прикладная математика
Учетные данные
Код модуля1127561
Учебный план в ЕИСУ № 6104
Код ОП
01.03.04/01.01
Код направления и уровня
подготовки
01.03.04
Уровень подготовки
Бакалавриат
ФГОС ВО
Реквизиты приказа Минобрнауки
РФ об утверждении ФГОС ВО:
12 марта 2015 г., № 208
Екатеринбург, 2017
89
90.
Рабочая программа дисциплины составлена авторами:№ п/п
ФИО
1
Тырсин Александр
Николаевич
Ученая степень,
ученое звание
Д-р техн. наук,
доцент
Руководитель модуля
Должность
Заведующи
й кафедрой
Кафедра
Подпись
Кафедра
прикладн
ой
математи
ки
А.Н. Сесекин
Рекомендовано учебно-методическим советом Уральского энергетического института
Председатель учебно-методического совета
Протокол № ______ от __________ г.
Е.В. Черепанова
Согласовано:
Дирекция образовательных программ
Р.Х. Токарева
90
91.
6. ОБЩАЯ ХАРАКТЕРИСТИКА ДИСЦИПЛИНЫ ТЕОРИЯ ВЕРОЯТНОСТЕЙ ИМАТЕМАТИЧЕСКАЯ СТАТИСТИКА
1.6.Аннотация содержания дисциплины
Дисциплина относится к модулю «Специальные главы математики» (базовая часть).
Дисциплины модуля: Теория функций комплексного переменного (3 семестр), Обыкновенные
дифференциальные уравнения. Теория устойчивости (3, 4 семестры), Дискретная математика
(3,4 семестры), Функциональный анализ (3 семестр), Введение в специальность (4 семестр).
Дисциплина «Теория вероятностей и математическая статистика» опирается на
теоретический аппарат, изученный в курсах «Алгебра и аналитическая геометрия»,
«Математический анализ».
Теория вероятностей и математическая статистика дают мощный инструмент для
описания и математического моделирования реальных процессов в механике, физике и других
областях знания. Цель курса «Теория вероятностей и математическая статистика» состоит в
том, чтобы ознакомить студентов с базовыми понятиями статистического анализа и научить
применять теоретико-вероятностные методы в приложениях.
Полученные знания, умения и навыки студенты будут применять в дисциплинах
«Прикладная статистика», «Теория случайных процессов» и «Теория массового
обслуживания» модуля «Случайные процессы и статистика», в других учебных курсах, в
дипломном проектировании и в профессиональной сфере.
1.2. Язык реализации программы – русский.
1.3. Планируемые результаты обучения по дисциплине
Результатом обучения в рамках дисциплины является формирование у студента
следующих компетенций:
- ОПК1 – готовность к самостоятельной работе (ОПК-1);
- ОПК2 – способность использовать современные математические методы и современные
прикладные программные средства и осваивать современные технологии программирования
(ОПК-2);
- ПК9 – способность выявить естественнонаучную сущность проблем, возникающих в ходе
профессиональной деятельности, готовность использовать для их решения соответствующий
естественнонаучный аппарат (ПК-9);
- ПК10 – готовность применять математический аппарат для решения поставленных задач,
способность применить соответствующую процессу математическую модель и проверить ее
адекватность (ПК-10);
- ПК-11 - готовность применять знания и навыки управления информацией;
- ПК12 – способность самостоятельно изучать новые разделы фундаментальных наук (ПК-12).
В результате освоения дисциплины студент должен:
Знать:
- основные принципы, методы и результаты современной теории вероятностей и
математической статистики;
- основные понятия, теоретические положения и теоремы теории вероятностей;
- основы математической статистики.
Уметь:
- вычислять вероятностные характеристики случайных величин и случайных процессов;
- обрабатывать статистические данные;
- строить адекватные теоретико-вероятностные и статистические модели реальных процессов
и явлений и проводить их математический анализ.
Владеть (демонстрировать навыки и опыт деятельности): методами классической теории
вероятностей и методами точечного и статистического анализа.
91
92.
21.4.Объем дисциплины
Объем дисциплины
№
п/
п
Виды учебной работы
1.
2.
3.
4.
5.
6.
7.
8.
Распределение объема
дисциплины по семестрам (час.)
Всего
часов
В т.ч.
контактн
ая работа
(час.)*
4
Аудиторные занятия
Лекции
Практические занятия
Лабораторные работы
Самостоятельная работа студентов,
включая все виды текущей
аттестации
Промежуточная аттестация
68
34
34
68
34
34
68
34
34
18
2,33
Общий объем по учебному плану,
час.
Общий объем по учебному плану,
з.е.
144
80,53
10,2
58
4
58
Э,18
144
4
*Контактная работа составляет:
в п/п 2,3,4 - количество часов, равное объему соответствующего вида занятий;
в п.5 – количество часов, равное сумме объема времени, выделенного преподавателю на консультации в
группе (15% от объема аудиторных занятий) и объема времени, выделенного преподавателю на руководство
курсовой работой/проектом одного студента, если она предусмотрена.
в п.6 – количество часов, равное сумме объема времени, выделенного преподавателю на проведение
соответствующего вида промежуточной аттестации одного студента и объема времени, выделенного в рамках
дисциплины на руководство проектом по модулю (если он предусмотрен) одного студента.
22. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
Код
Раздел, тема
раздела,
дисциплины*
темы
Р1
Основные понятия
теории вероятностей.
Случайные события
Р2
Случайные величины и
их распределения
Р3
Виды сходимости
последовательностей
случайных величин
Р4
Основные понятия
математической
Содержание
Основные понятия теории вероятностей. Случайные
события и их описание. Непосредственное
вычисление вероятностей. Сумма и произведение
событий. Геометрические вероятности. Формула
полной вероятности и формула Байеса. Повторение
опытов. Схема Бернулли.
Случайные величины (СВ). Законы распределения
случайных величин и их формы. Типичные
дискретные и абсолютно непрерывные
распределения. Математическое ожидание,
дисперсия. Мода и медиана. Центральные и
начальные моменты СВ. Функции от случайных
величин. Многомерные случайные величиныю
Предельные теоремы для схемы Бернулли.
Неравенства Чебышева. Теорема Чебышева. Закон
больших чисел. Характеристические функции СВ.
Центральная предельная теорема.
Основы выборочного метода. Вариационные ряды.
Понятие оценки параметров. Построение законов
92
93.
статистикираспределения СВ по статистическим данным.
Точечные оценки параметров распределений
методами моментов, максимального правдоподобия,
наименьших квадратов. Интервальные оценки
параметров распределений. Статистическая проверка
гипотез, общая схема проверки, уровень значимости,
ошибки первого и второго рода. Критерии согласия,
гипотезы о числовых характеристиках случайных
величин, гипотезы о стохастической независимости
элементов выборки.
23. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ
3.6. Распределение аудиторной нагрузки и мероприятий самостоятельной работы по
разделам дисциплины
Очная форма обучения
93
94.
Объем модуля (зач.ед.): 27Объем дисциплины (зач.ед.): 4
Подготовка к
контрольным
мероприятиям
текущей
аттестации
(колич.)
5
5
8
58
38
19
19
16
76
4
4
0
18
0
0
1
8
8
В т.ч. промежуточная аттестация
94
Проект по модулю
10
1
Интегрированный экзамен по модулю
18
2
Экзамен
1
1
Подго
товка
в
рамка
х
дисци
плины
к
проме
жуточ
ной
аттест
ации
по
модул
ю
(час.)
Зачет
4
2
Подготов
ка к
промежут
очной
аттестац
ии по
дисципли
не (час.)
Коллоквиум*
5
Контрольная работа*
5
Всего (час.)
10
Курсовой проект*
16
Курсовая работа*
1
Перевод инояз. литературы*
4
Домашняя работа на иностр.
языке*
5
Расчетно-графическая работа*
5
Расчетная работа, разработка
программного продукта*
10
Проектная работа*
14
Реферат, эссе, творч. работа*
4
Графическая работа*
4
Домашняя работа*
8
Всего (час.)
10
Лабораторное занятие
Практ., семинар. занятие
Выполнение самостоятельных внеаудиторных работ
(колич.)
Лекция
Н/и семинар, семинар-конфер.,
коллоквиум (магистратура)
Подготовка к аудиторным
занятиям (час.)
Всего (час.)
26
16
Основные понятия теории
8
8
вероятностей. Случайные
события.
32
18
Р2 Случайные величины и их
8
10
распределения.
30
14
Р3
Виды сходимости
8
6
последовательностей случайных
величин.
38
20
Р4 Основные понятия
10
10
математической статистики.
Всего (час), без учета
126
68
34
34
промежуточной аттестации:
Всего по дисциплине (час.):
144
68
*Суммарный объем в часах на мероприятие
указывается в строке «Всего (час.) без учета промежуточной аттестации
Р1
Самостоятельная работа: виды, количество и объемы мероприятий
Всего самостоятельной работы студентов (час.)
Лабораторные работы
Практические занятия
Лекции
Всего по разделу, теме (час.)
Код раздела, темы
Наименование раздела, темы
Всего аудиторной работы (час.)
Аудиторные занятия
(час.)
Раздел дисциплины
95.
9596.
24. ОРГАНИЗАЦИЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ, САМОСТОЯТЕЛЬНОЙ РАБОТЫПО ДИСЦИПЛИНЕ
6.11.
Лабораторные работы
Не предусмотрено
Практические занятия
Код
раздела,
темы
6.12.
Номер
занятия
Р1
1
Р1
2
Р1
3
Р1
4
Р2
5
Р2
6
Р2
Р2
7
8
Р2
9
Р3
10
Р3
11
Р3
12
Р4
13
Р4
14
Р4
15
Р4
16
Р4
17
Тема занятия
Классическое определение вероятности.
Элементарные свойства вероятности.
Геометрическая вероятность.
Условная вероятность. Теорема умножения
вероятностей.
Формулы полной вероятности. Формула Байеса.
Схема Бернулли.
Дискретные случайные величины и их
распределения.
Непрерывные случайные величины и их
распределения.
Числовые характеристики случайных величин.
Распределение функции от случайной величины.
Многомерные случайные величины.
Независимость и некоррелированность
случайных величин
Предельные теоремы для схемы Бернулли.
Неравенства Чебышева. Теорема Чебышева.
Закон больших чисел.
Характеристические функции случайных
величин. Центральная предельная теорема.
Основы выборочного метода. Вариационные
ряды. Понятие оценки параметров. Построение
законов распределения СВ по статистическим
данным.
Точечные оценки параметров распределений
методами моментов, максимального
правдоподобия, наименьших квадратов.
Интервальные оценки параметров
распределений.
Статистическая проверка гипотез, общая схема
проверки, уровень значимости, ошибки первого
и второго рода.
Критерии согласия, однородности, гипотезы о
числовых характеристиках случайных величин,
гипотезы о стохастической независимости
элементов выборки.
Всего:
96
Время на
проведение
занятия (час.)
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
34
97.
8. 4.3.Примерная тематика самостоятельной работы4.3.16. Примерный перечень тем домашних работ
Домашняя работа № 1.
Дискретные и непрерывные случайные величины и их распределение.
Домашняя работа № 2.
Предельные теоремы.
4.3.17. Примерный перечень тем графических работ
Не предусмотрено.
4.3.18. Примерный перечень тем рефератов (эссе, творческих работ)
Не предусмотрено.
4.3.4
Примерная тематика индивидуальных или групповых проектов
Не предусмотрено.
4.3.22. Примерный перечень тем расчетных работ (программных продуктов)
Расчетная работа № 1
Основы математической статистики
4.3.23. Примерный перечень тем расчетно-графических работ
Не предусмотрено.
4.3.24. Примерный перечень тем курсовых проектов (курсовых работ)
Не предусмотрено.
24.4.1. Примерная тематика контрольных работ
Контрольная работа № 1.
Случайные события.
Контрольная работа № 2.
Виды сходимости последовательностей случайных величин.
4.3.9. Примерная тематика коллоквиумов
Не предусмотрено.
25. СООТНОШЕНИЕ РАЗДЕЛОВ, ТЕМ ДИСЦИПЛИНЫ И ПРИМЕНЯЕМЫХ
ТЕХНОЛОГИЙ ОБУЧЕНИЯ
Р1
*
Р2
*
Р3
*
*
Р4
*
*
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ
(Приложение 1)
97
Другие (указать, какие)
Вебинары и
видеоконференции
Асинхронные webконференции и семинары
Совместная работа и
разработка контента
Виртуальные практикумы
и тренажеры
Сетевые учебные курсы
Другие (указать, какие)
Командная работа
Проблемное обучение
Деловые игры
Кейс-анализ
Код раздела, темы
дисциплины
Проектная работа
Активные методы обучения
Дистанционные
образовательные технологии и
электронное обучение
98.
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХНЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ (Приложение 2)
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ (Приложение 3)
9. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ
ДИСЦИПЛИНЫ
9.1.Рекомендуемая литература
9.1.1.Основная литература
1. Вентцель, Е.С. Задачи и упражнения по теории вероятностей: Учеб. пособие для
студентов втузов / Е.С. Вентцель, Л.А. Овчаров. — 5-е изд., испр. — М.: Академия,
2004. — 448 с. — ISBN 5-7695-1054-4 (ЗНБ УрФУ).
2. Вентцель, Е.С. Теория вероятностей: Учебник для вузов. — 6-е изд., стер. — М.:
Высшая школа, 1999. — 576 с. — ISBN 5-06-003650-2 (ЗНБ УрФУ).
3. Гнеденко, Б.В. Курс теории вероятностей: Учебник для студентов мат.
специальностей ун-тов / Б.В. Гнеденко. — 8-е изд., испр. и доп. — М.: УРСС, 2005. —
448 с. — ISBN 5-354-01091-8 (ЗНБ УрФУ).
4. Коршунов, Д.А. Сборник задач и упражнений по теории вероятностей : Учеб. пособие
/ Д.А. Коршунов, С.Г. Фосс, И.М. Эйсымонт. — СПб.; Лань, 2004. — 192 с. — ISBN
5-8114-0587-1 (ЗНБ УрФУ).
5. Прохоров, Ю.В. Теория вероятностей. Основные понятия. Предельные теоремы.
Случайные процессы. — 3-е изд., перераб. — М.: Наука, 1987. — 397 с. (ЗНБ УрФУ).
6. Севастьянов, Б.А. Курс теории вероятностей и математической статистики: Учебник
для спец. "Математика" и "Механика" / Б.А. Севастьянов. — М.: Наука, 1982. — 255
с. (ЗНБ УрФУ).
7. Семенчин, Е.А. Теория вероятностей в примерах и задачах: Учеб. пособие для
студентов вузов, обучающихся по специальности "Прикладная математика" / Е.А.
Семенчин. — СПб.: Лань, 2007. — 352 с. — ISBN 978-5-8114-0648-7 (ЗНБ УрФУ).
8. Теория вероятностей: Учебник для студентов втузов / Под ред. В.С. Зарубина, А.П.
Крищенко. — 3-е изд., испр. — М.: Издательство МГТУ им. Н. Э. Баумана, 2004 .—
456 с. — ISBN 5-7038-2485-0 (ЗНБ УрФУ).
9. Математическая статистика : учебник для студентов втузов / Под ред. В.С. Зарубина,
А.П. Крищенко. — М.: Издательство МГТУ им. Н.Э. Баумана, 2001. — 424 с. — ISBN
5-7038-1270-4 (ЗНБ УрФУ).
10. Ширяев, А.Н. Вероятность: Учеб. пособие для ун-тов по специальности "Математика"
/ А.Н. Ширяев. — М.: Наука, 1980. — 575 с. (ЗНБ УрФУ).
9.1.2. Дополнительная литература
11. Большев, Л.Н. Таблицы математической статистики / Л.Н. Большев, Н.В. Смирнов. —
Москва : Наука, 1983 .— 416 с. (ЗНБ УрФУ).
12. Боровков, А.А. Математическая статистика: Оценка параметров. Проверка гипотез :
Учеб. пособие для мат. и физ. специальностей вузов / А.А. Боровков. — М.: Наука,
1984. — 472 с. (ЗНБ УрФУ).
13. Босс, В. Лекции по математике. Т.4. Вероятность, информация, статистика / В. Босс.
— М.: КомКнига, 2005. — 216 с. — ISBN 5-484-00168-4 (ЗНБ УрФУ).
14. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и
математической статистике: Учеб. пособие для студентов вузов / В.Е. Гмурман. — 11е изд., перераб. — М.: Высшее образование, 2006. — 404 с. — ISBN 5-9692-0103-0
(ЗНБ УрФУ).
98
99.
15. Кобзарь, А.И. Прикладная математическая статистика. Для инженеров и научныхработников / А.И. Кобзарь. — М.: ФИЗМАТЛИТ, 2006. — 816 с. — ISBN 5-92210707-0 (ЗНБ УрФУ).
16. Монсик, В.Б. Вероятность и статистика: Учеб. пособие для втузов / В.Б. Монсик, А.А.
Скрынников. — М.: БИНОМ. Лаборатория знаний, 2014. — 381 с. — ISBN 978-59963-0637-4 (ЗНБ УрФУ).
17. Свешников, А.А. Прикладные методы теории вероятностей: Учебник для студентов
вузов / А.А. Свешников. — СПб.: Лань, 2012. — 480 с. — ISBN 978-5-8114-1219-8
(ЗНБ УрФУ).
18. Секей, Г. Парадоксы в теории вероятностей и математической статистике / Г. Секей;
пер. с англ. — М.: Мир, 1990. — 240 с. — ISBN 5-03-001293-1 (ЗНБ УрФУ).
9.2. Методические разработки
19. Голикова, Е.А. Элементы теории вероятностей: Учеб. пособие для студентов,
обучающихся по программе бакалавриата и специалитета по направлениям
подготовки 010900.62 "Прикладные математика и физика", 140800.62 "Ядерные
физика и технологии", 210100.62 "Электроника и наноэлектроника", 201000
"Биотехнические системы и технология", 200100 "Приборостроение", 221700
"Стандартизация и метрология". — Екатеринбург: УрФУ, 2012. — 126 с. — ISBN 9785-321-02152-1 (ЗНБ УрФУ).
20. Грахов, В.Б. Математическая статистика в примерах и задачах: Учеб. пос. / В.Б.
Грахов. — Екатеринбург: УГТУ-УПИ, 2009. — 126 с. — ISBN 978-5-321-01573-5
(ЗНБ УрФУ).
21. Катальников, В.В. Сборник задач по теории вероятностей: Учеб. пособие / В.В.
Катальников, Ю.В. Шапарь. — Екатеринбург: УГТУ-УПИ, 2007. — 73 с. — ISBN 9785-321-01020-4 (ЗНБ УрФУ).
9.3. Программное обеспечение
MS Office.
9.4. Базы данных, информационно-справочные и поисковые системы
https://www.coursera.org/ – массовые открытые онлайн-курсы;
https://www.edx.org/ – массовые открытые онлайн-курсы;
https://openedu.ru/ – национальная платформа открытого образования;
http://poiskknig.ru – электронная библиотека учебников Мех-Мата МГУ, Москва;
http://www.mathnet.ru. – общероссийский математический портал;
http://lib.urfu.ru – зональная научная библиотека УрФУ.
9.5.Электронные образовательные ресурсы
УМК № 10858 «Математика» (режим доступа: https://study.urfu.ru/Aid/ViewMeta/10858).
10. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Сведения об оснащенности дисциплины специализированным и лабораторным
оборудованием
1. Лекционные специализированные аудитории с видеопроекционным комплексом на
базе мультимедийного проектора и персонального компьютера: Т-1202б, Т-1208.
2. Компьютерные классы и аудитории для проведения лабораторных работ: Т-1208, Т1202б, Т-1202.
99
100.
ПРИЛОЖЕНИЕ 1к рабочей программе дисциплины
6. ПРОЦЕДУРЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В
РАМКАХ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
6.1. Весовой коэффициент значимости дисциплины –
6.2. Процедуры текущей и промежуточной аттестации по дисциплине
1.Лекции: коэффициент значимости совокупных результатов лекционных занятий – 0,6
Текущая аттестация на лекциях
Сроки –
Максималь
семестр,
ная оценка
учебная
в баллах
неделя
Экспертиза конспекта
4, 1-17
100
Весовой коэффициент значимости результатов текущей аттестации по лекциям – 0,4
Промежуточная аттестация по лекциям – экзамен*
Весовой коэффициент значимости результатов промежуточной аттестации по лекциям –
0,6
2. Практические/семинарские занятия: коэффициент значимости совокупных
результатов практических/семинарских занятий – 0,4
Текущая аттестация на практических/семинарских
Сроки –
Максималь
занятиях
семестр,
ная оценка
учебная
в баллах
неделя
Работа на практическом занятии
4, 1-17
28
Домашняя работа № 1
4, 1-17
10
Домашняя работа № 2
4, 1-17
10
Контрольная работа № 1
4, 1-17
20
Контрольная работа № 2
4, 1-17
20
Расчетная работа № 1
4, 1-17
12
Весовой коэффициент значимости результатов текущей аттестации по
практическим/семинарским занятиям – 1
Промежуточная аттестация по практическим/семинарским занятиям – нет
Весовой коэффициент значимости результатов промежуточной аттестации по
практическим/семинарским занятиям – 0
3. Лабораторные занятия: коэффициент значимости совокупных результатов
лабораторных занятий – не предусмотрено
6.3. Процедуры текущей и промежуточной аттестации курсовой работы
Не предусмотрено
6.4. Коэффициент значимости семестровых результатов освоения дисциплины
Порядковый номер семестра по учебному
Коэффициент значимости результатов
плану, в котором осваивается дисциплина
освоения дисциплины в семестре
Семестр 4
1
*В случае проведения промежуточной аттестации по дисциплине (экзамена, зачета) методом
тестирования используются официально утвержденные ресурсы: АПИМ УрФУ, СКУД
УрФУ, имеющие статус ЭОР УрФУ; ФЭПО (www.фэпо.рф); Интернет-тренажеры (www.iexam.ru).
100
101.
ПРИЛОЖЕНИЕ 2к рабочей программе дисциплины
7. ПРОЦЕДУРЫ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ В РАМКАХ
НЕЗАВИСИМОГО ТЕСТОВОГО КОНТРОЛЯ
Не предусмотрено
101
102.
ПРИЛОЖЕНИЕ 3к рабочей программе дисциплины
8. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ И
ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО ДИСЦИПЛИНЕ
8.1. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ КОНТРОЛЬНО-ОЦЕНОЧНЫХ
МЕРОПРИЯТИЙ ТЕКУЩЕЙ И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ПО
ДИСЦИПЛИНЕ В РАМКАХ БРС
В рамках БРС применяются утвержденные на кафедре критерии оценивания
достижений студентов по каждому
контрольно-оценочному мероприятию. Система
критериев оценивания, как и при проведении промежуточной аттестации по модулю,
опирается на три уровня освоения компонентов компетенций: пороговый, повышенный,
высокий.
Компоненты
Признаки уровня освоения компонентов компетенций
компетенций
пороговый
повышенный
высокий
Студент демонстрирует
Студент демонстрирует Студент может
Знания
знание-знакомство,
аналитические знания:
самостоятельно
знание-копию: узнает
уверенно воспроизводит извлекать новые знания
объекты, явления и
и понимает полученные из окружающего мира,
понятия, находит в них
знания, относит их к той творчески их
различия, проявляет
или иной
использовать для
знание источников
классификационной
принятия решений в
получения информации,
группе, самостоятельно новых и нестандартных
может осуществлять
систематизирует их,
ситуациях.
самостоятельно
устанавливает
репродуктивные действия взаимосвязи между
над знаниями путем
ними, продуктивно
самостоятельного
применяет в знакомых
воспроизведения и
ситуациях.
применения информации.
Студент умеет корректно
Студент умеет
Студент умеет
Умения
выполнять предписанные самостоятельно
самостоятельно
действия по инструкции,
выполнять действия
выполнять действия,
алгоритму в известной
(приемы, операции) по
связанные с решением
ситуации, самостоятельно решению нестандартных исследовательских
выполняет действия по
задач, требующих
задач, демонстрирует
решению типовых задач,
выбора на основе
творческое
требующих выбора из
комбинации известных использование умений
числа известных методов, методов, в
(технологий)
в предсказуемо
непредсказуемо
изменяющейся ситуации
изменяющейся ситуации
Студент имеет
Студент имеет
Личностные Студент имеет низкую
мотивацию учебной
выраженную мотивацию развитую мотивацию
качества
деятельности, проявляет
учебной деятельности,
учебной и трудовой
безразличное,
демонстрирует
деятельности,
безответственное
позитивное отношение к проявляет
отношение к учебе,
обучению и будущей
настойчивость и
порученному делу
трудовой деятельности, увлеченность,
проявляет активность.
трудолюбие,
самостоятельность,
102
103.
творческий подход.8.2. КРИТЕРИИ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ПРОМЕЖУТОЧНОЙ
АТТЕСТАЦИИ ПРИ ИСПОЛЬЗОВАНИИ НЕЗАВИСИМОГО ТЕСТОВОГО
КОНТРОЛЯ
При проведении независимого тестового контроля как формы промежуточной
аттестации применяется методика оценивания результатов, предлагаемая разработчиками
тестов. Процентные показатели результатов независимого тестового контроля переводятся в
баллы промежуточной аттестации по 100-балльной шкале в БРС:
в случае балльной оценки по тесту (блокам, частям теста) переводится процент набранных
баллов от общего числа возможных баллов по тесту;
при отсутствии балльной оценки по тесту переводится процент верно выполненных
заданий теста, от общего числа заданий.
8.3. ОЦЕНОЧНЫЕ СРЕДСТВА ДЛЯ ПРОВЕДЕНИЯ ТЕКУЩЕЙ
И ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
8.3.1. Примерные задания для проведения домашних работ
Домашняя работа № 1.
1. Случайная величина X задана функцией распределения
x / 2
0,
F ( X ) cos x, / 2 x 0.
1,
x 0
Найти M ( X ), D( X ), ( X ). Построить график функции распределения и график
плотности распределения.
Домашняя работа № 1.
1. В течение времени t эксплуатируются 500 приборов. Каждый прибор имеет
надежность 0,98 и выходит из строя независимо от других. Оценить с помощью неравенства Чебышева вероятность того, что доля надежных приборов отличается от 0,98
не более чем на 0,1 (по абсолютной величине).
8.3.2. Примерные контрольные задачи в рамках учебных занятий
Контрольная работа № 1.
2. Монета бросается до тех пор, пока 2 раза подряд она не выпадет одной и той же
стороной. Найти вероятности следующих событий: а) опыт окончится до шестого
бросания; б) потребуется четное число бросаний.
Контрольная работа № 2.
1. При штамповке пластинок из пластмассы брак составляет 3 %. Найти вероятность
того, что при проверке партии в 1000 пластинок выявится отклонение от
установленного процента брака меньше чем на 1 %.
8.3.3. Примерные задания для проведения расчетной работы
Расчетная работа № 1.
1. Из генеральной совокупности извлечена выборка объема. Оценить с надежностью
0,95 математическое ожидание а нормально распределенного признака генеральной
совокупности с помощью доверительного интервала.
103
104.
xi-4
0
1
2
3
4
ni
1
3
5
4
2
1
8.3.4. Примерные контрольные кейсы
Не предусмотрено
8.3.4. Перечень примерных вопросов для зачета
Не предусмотрено
8.3.5. Перечень примерных вопросов для экзамена
События и их вероятности
1. Теорема о перемножении шансов. Урновые схемы: выбор с возвращением и без, с учетом
порядка и без. Число возможных результатов в каждой из схем выбора (без доказательства в
схеме выбора с возвращением без учета порядка).
2. Пространство элементарных исходов. Определение события. Операции над событиями:
объединение, пересечение, дополнение одного события до другого, противоположное
событие. Достоверное и невозможное события.
3. Вероятность на дискретном пространстве элементарных исходов.
4. Классическое определение вероятности. Урновые схемы, удовлетворяющие и не
удовлетворяющие классическому определению вероятности. Гипергеометрическое
распределение.
5. Геометрическая вероятность. Задача о встрече. Задача Бюффона. Парадокс Бертрана.
6. Определение и свойства -алгебры событий. Примеры (в том числе борелевская -алгебра
на прямой). Определение меры и вероятностной меры. Свойства вероятности. Вероятность
объединения n событий (с доказательством). Определение вероятностного пространства.
7. Условные вероятности. Теорема умножения (вероятность пересечения двух и более
событий - с доказательством). Независимость пары событий. Независимость и
несовместность. Свойства независимых событий. Независимость в совокупности. Пример
Бернштейна.
8. Полная группа событий. Формулы полной вероятности и Байеса.
9. Схема Бернулли. Формула Бернулли (распределение числа успехов). Биномиальное
распределение. Наиболее вероятное число успехов . Геометрическое распределение.
Свойство «нестарения» геометрического распределения.
10. Приближение гипергеометрического распределения биномиальным. Распределение
Пуассона. Теорема Пуассона. Оценка погрешности (без доказательства).
Случайные величины и их распределения
1. Случайные величины. Измеримость относительно заданной -алгебры событий. Примеры
измеримых и неизмеримых отображений.
2. Дискретные распределения: определение, примеры.
3. Функция распределения и ее свойства
4. Абсолютно непрерывные распределения. Плотность распределения, ее свойства.
Существование случайной величины с заданной плотностью распределения. Свойства
функции распределения абсолютно непрерывного закона распределения.
5. Примеры абсолютно непрерывных распределений: равномерное, показательное (и для
него свойство «нестарения»), гамма, нормальное распределение.
6. Свойства нормального распределения: связь со стандартным нормальным распределением,
свойства функции распределения, правило «трех сигм».
7. Случайные вектора и их распределения. Дискретные и абсолютно непрерывные
многомерные распределения. Функция и плотность совместного распределения, их свойства.
Определение независимости случайных величин. Независимость случайных величин с
дискретным распределением. Независимость случайных величин с абсолютно непрерывным
совместным распределением: эквивалентные определения независимости в терминах
функций распределения и плотностей.
104
105.
8. Изменение плотности при линейных преобразованиях случайных величин. Примеры:показательное, равномерное, нормальное распределения. Формула свертки . Распределение
суммы двух независимых случайных величин со стандартным нормальным распределением.
9. Свойство устойчивости по суммированию. Распределения, обладающие этим свойством:
биномиальное, гамма распределение, распределение Пуассона, нормальное распределение.
10. Математическое ожидание и его свойства . Вычисление математических ожиданий
функций от случайных величин. Пример некоррелированных, но зависимых случайных
величин.
11. Моменты. Дисперсия. Свойства дисперсии.
12. Подсчет математических ожиданий, дисперсий и моментов стандартных распределений
(для распределений Бернулли, биномиального, Пуассона, равномерного, нормального –
математического ожидания и дисперсии, показательного).
13. Ковариация и коэффициент корреляции. Их свойства.
14. Двумерная дискретная случайная величина.
15. Многомерное нормальное распределение.
Предельные теоремы
1. Сходимость «почти наверное». Сходимость по вероятности. Неравенства Чебышева.
Определение закона больших чисел как свойства последовательности случайных величин.
Закон больших чисел в форме Чебышева. Достаточные условия выполнения закона больших
чисел для последовательности случайных величин. Закон больших чисел Бернулли. Закон
больших чисел в форме Хинчина.
2. Сходимость по распределению (слабая сходимость). Связь слабой сходимости со
сходимостью по вероятности.
3. Центральная предельная теорема, эквивалентные формулировки (без доказательства).
Теорема Муавра – Лапласа.
4. Характеристические функции. Их свойства. Доказательство ЗБЧ в форме Хинчина.
Доказательство ЦПТ. Доказательство свойства устойчивости нормального распределения
относительно суммирования. Доказательство свойств устойчивости распределения Пуассона,
гамма-распределения, биномиального распределения относительно суммирования методом
характеристических функций.
Элементы математической статистики
1. Основные распределения случайных величин, используемые в статистике.
2. Выборочный метод в статистике.
3. Первичная обработка статистических данных.
5. Точечные оценки параметров распределения. Критерии качества оценок.
5. Оценки среднего: выборочное среднее, мода, медиана.
6. Оценки вариации: выборочная дисперсия, стандартное отклонение, коэффициент
вариации.
7. Выборочная (эмпирическая) функция распределения .
8. Выборочная асимметрия и эксцесс.
9. Точность оценок. Доверительные интервалы.
10. Доверительный интервал для параметра m нормального распределения.
11. Доверительный интервал для дисперсии нормального распределения.
12. Проверка статистических гипотез.
13. Типичные задачи проверки гипотез о математическом ожидании ( t-критерий).
8.3.6. Ресурсы АПИМ УрФУ, СКУД УрФУ для проведения тестового контроля в
рамках текущей и промежуточной аттестации
Не используются.
8.3.7. Ресурсы ФЭПО для проведения независимого тестового контроля
Не используются.
8.3.8. Интернет-тренажеры
Не используются.
105

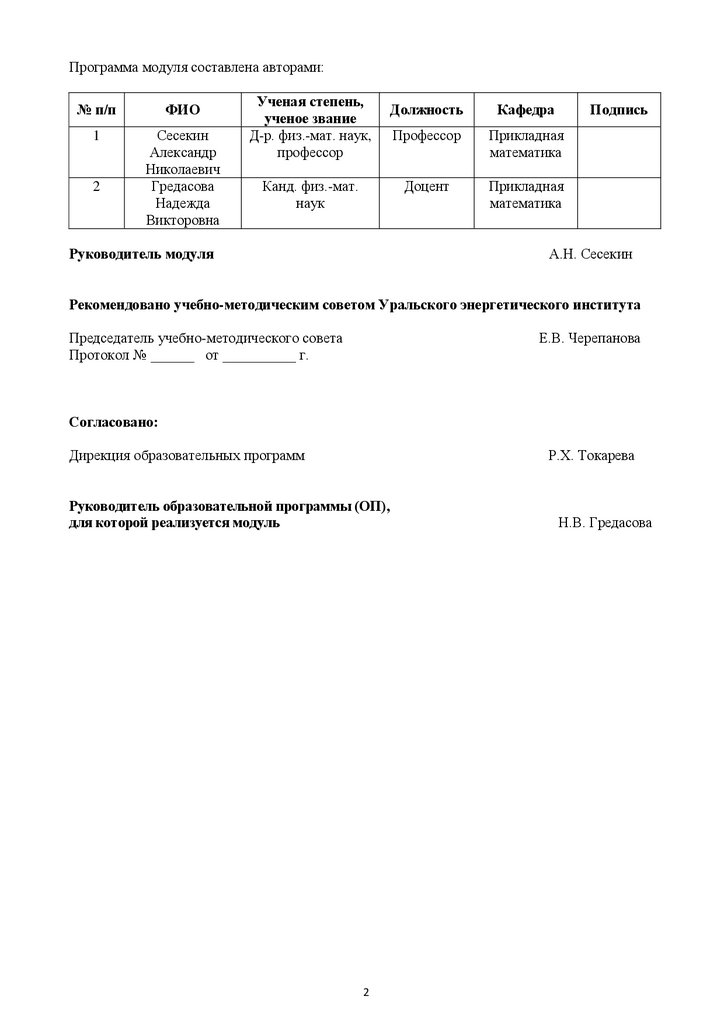
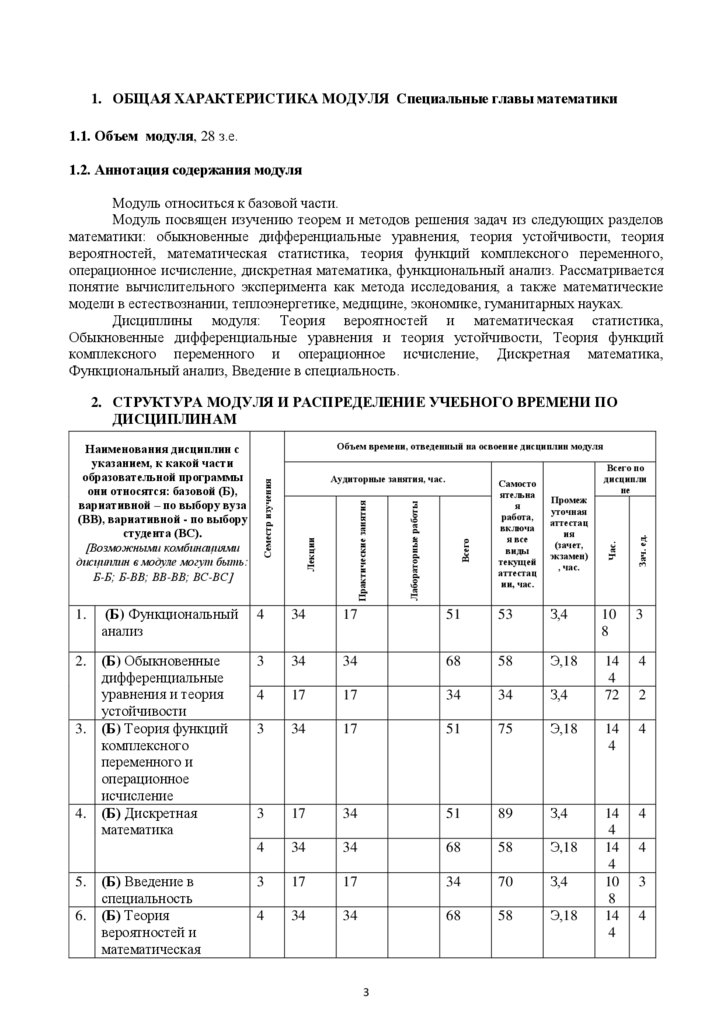


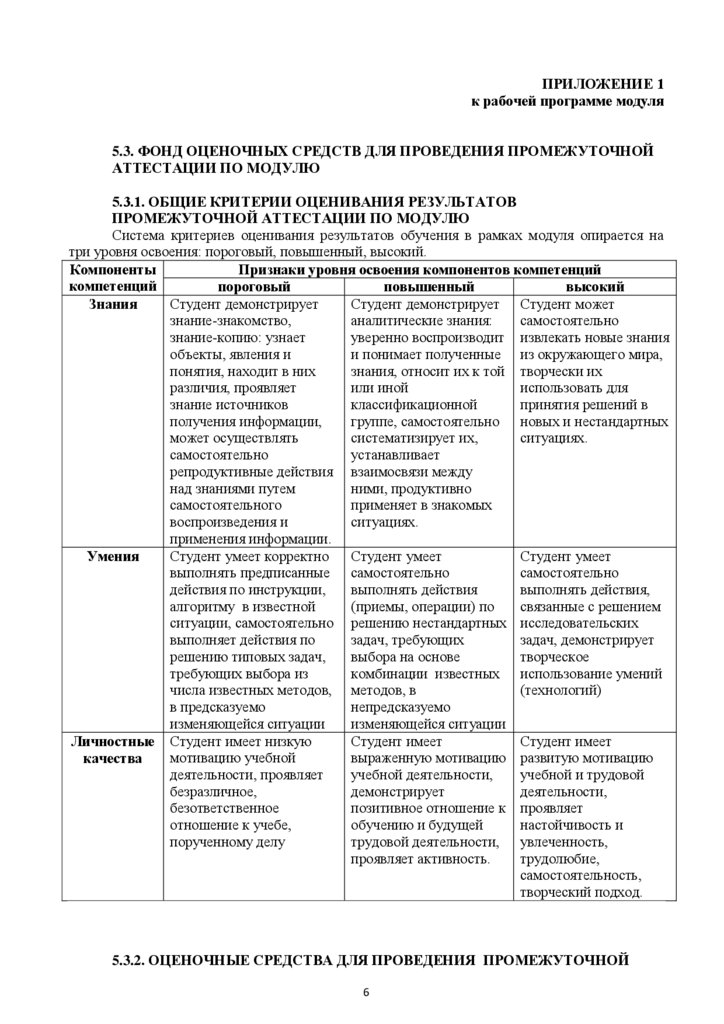




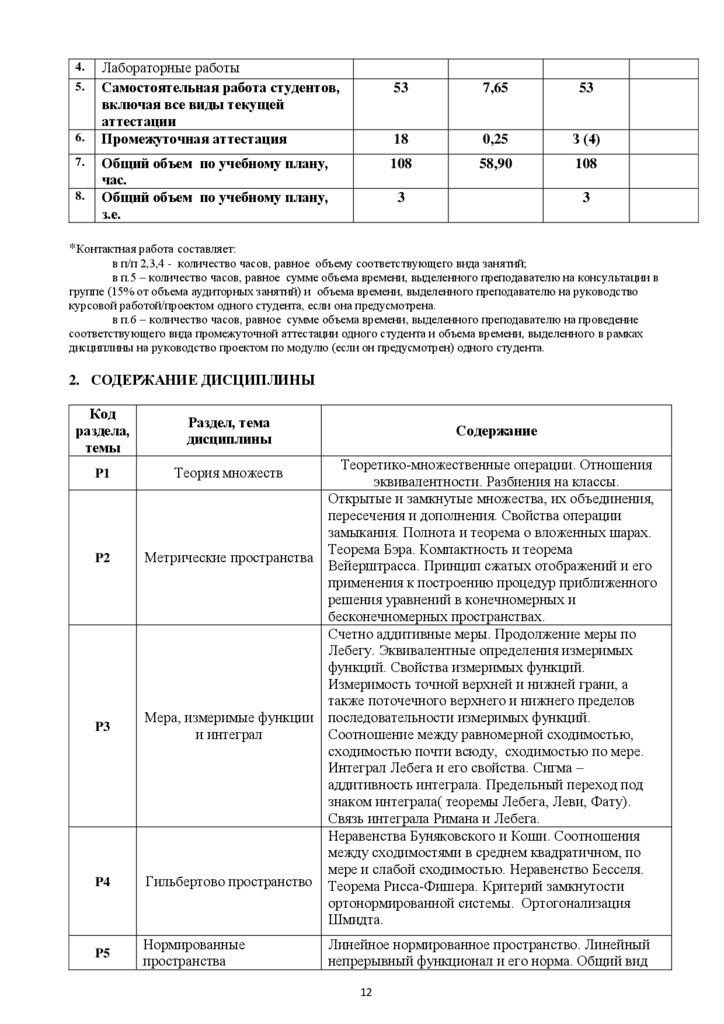

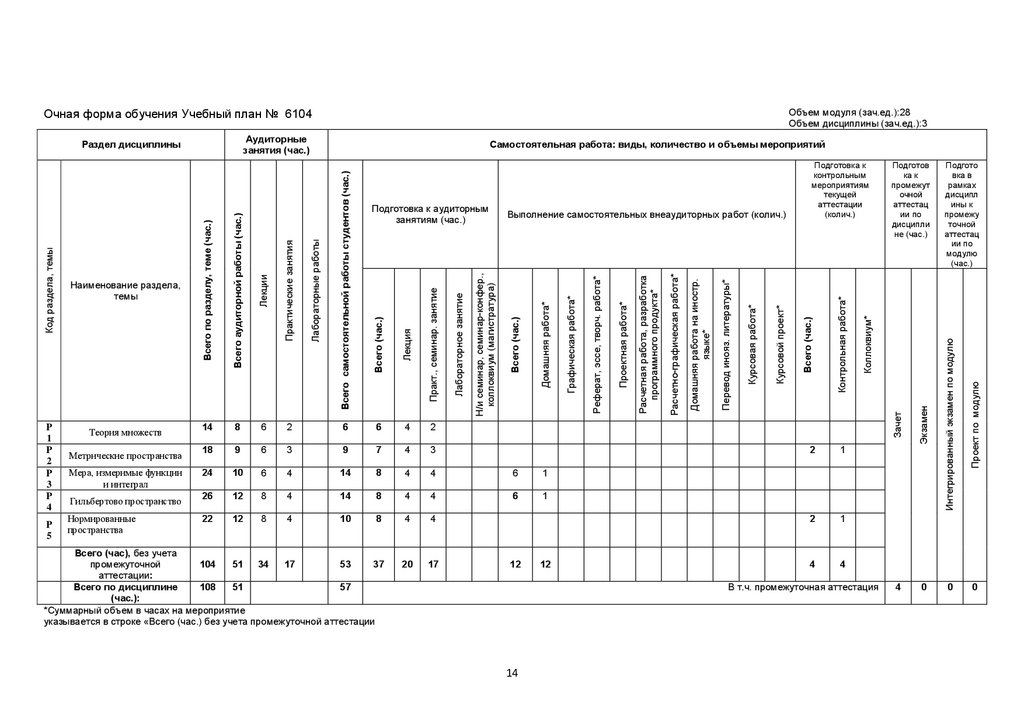
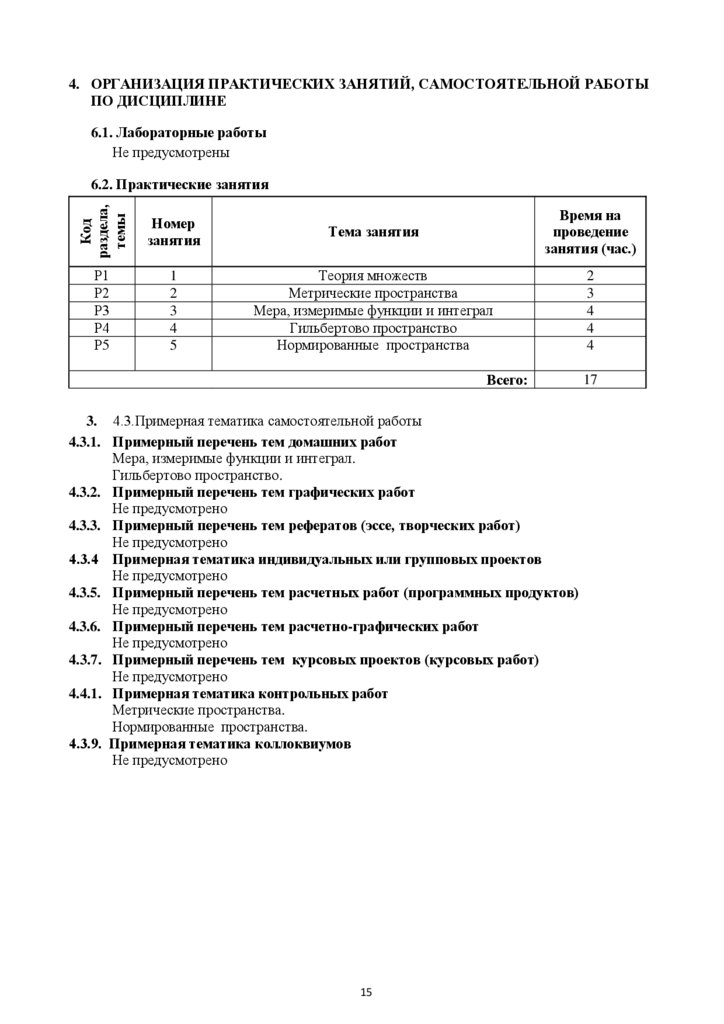



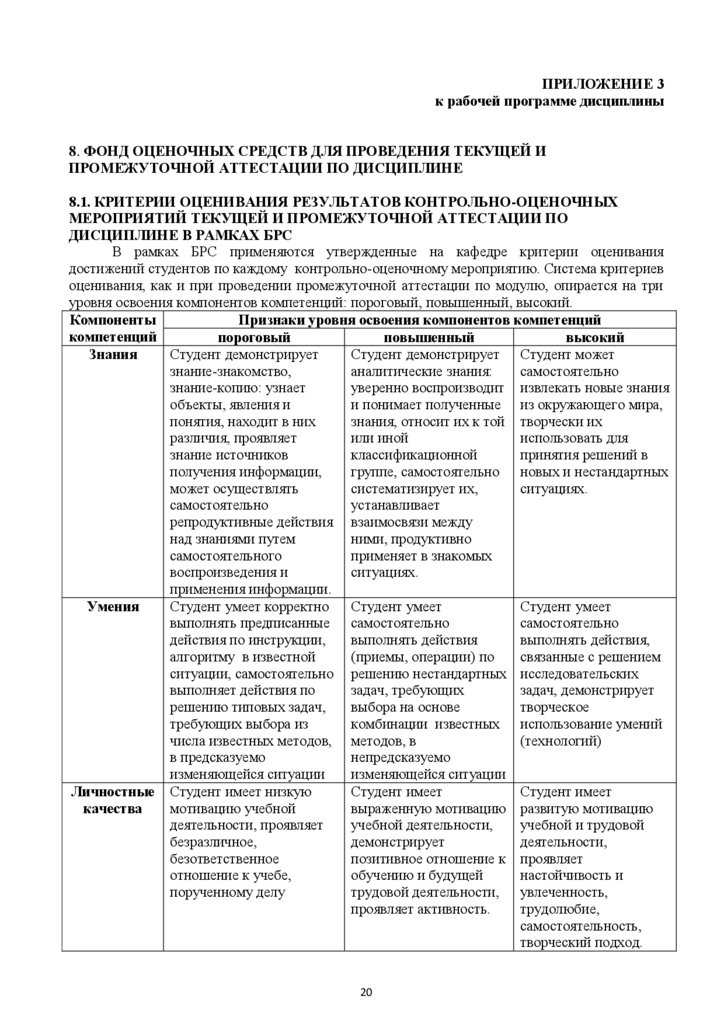





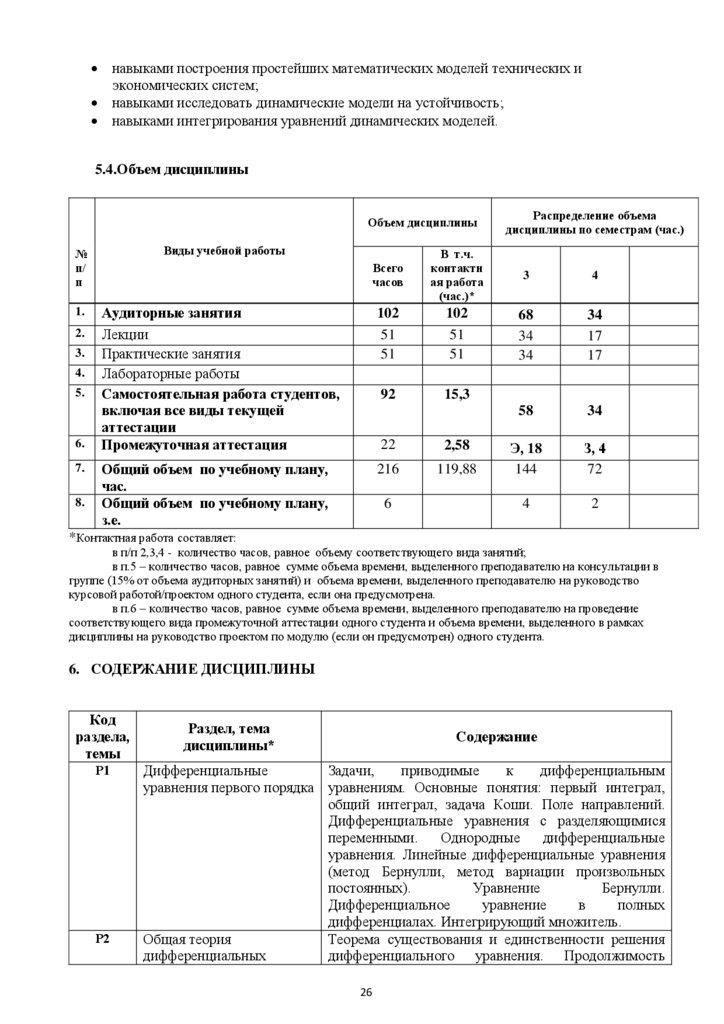


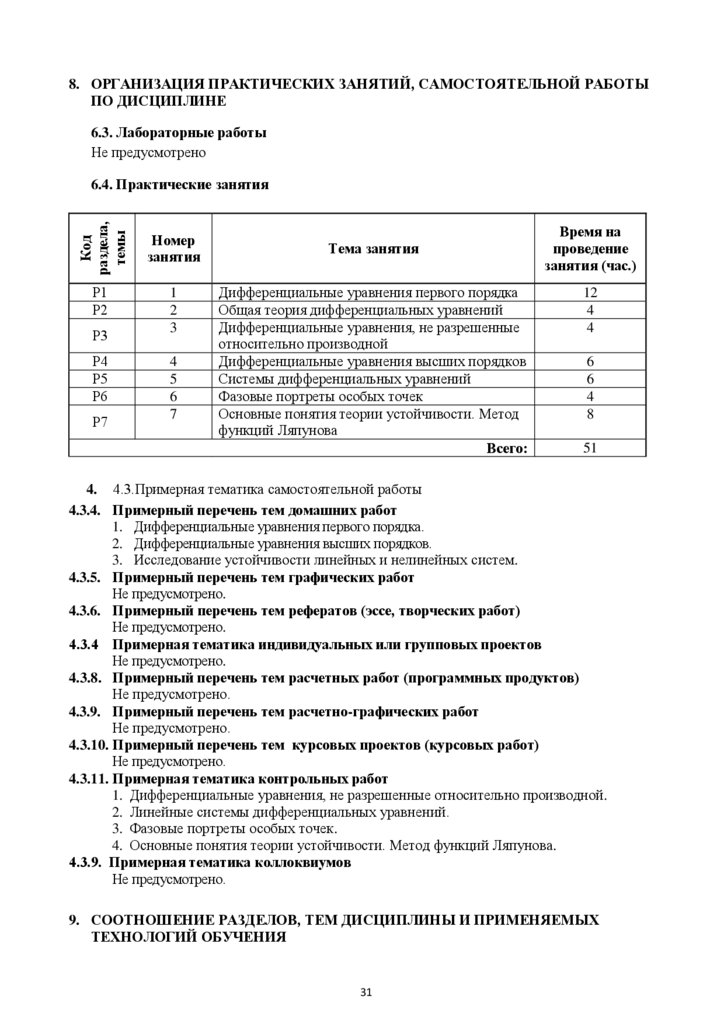


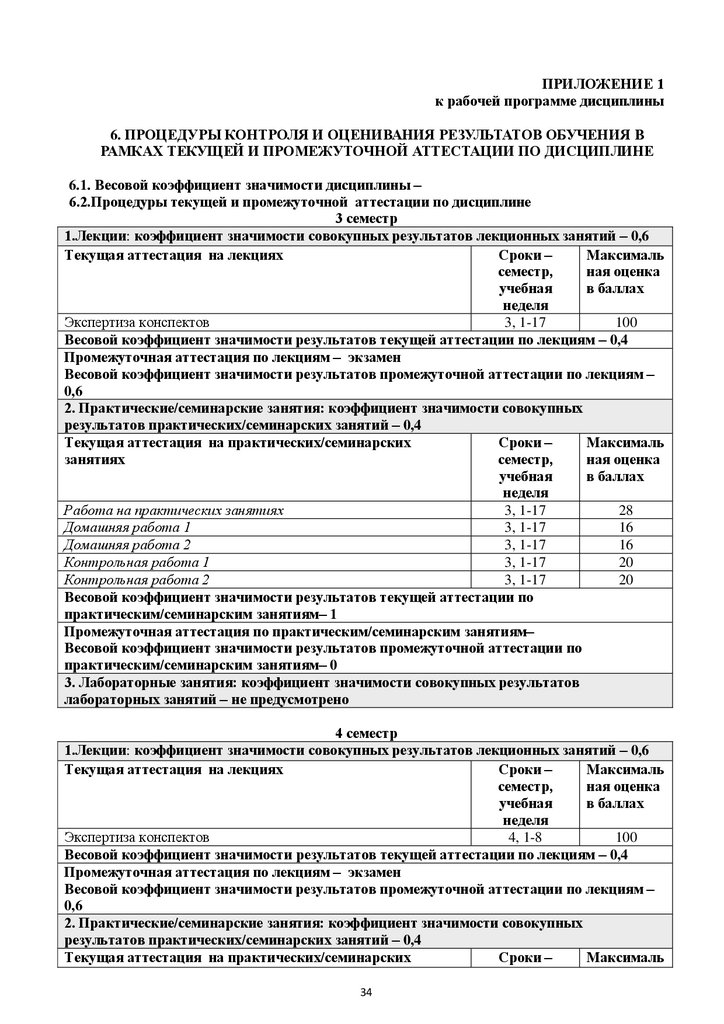


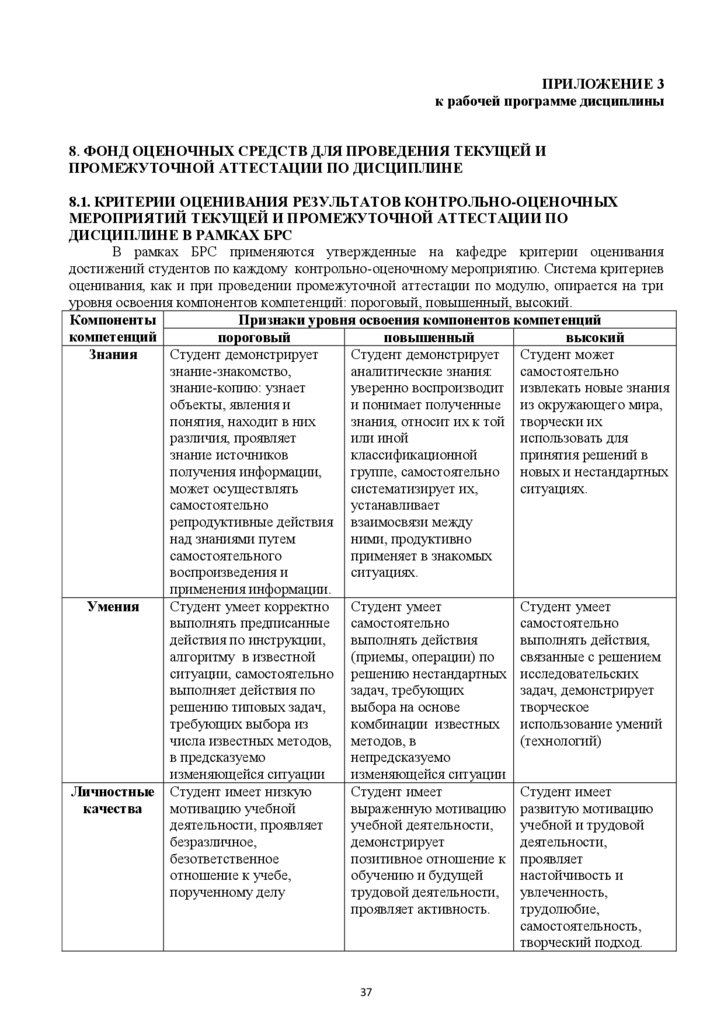





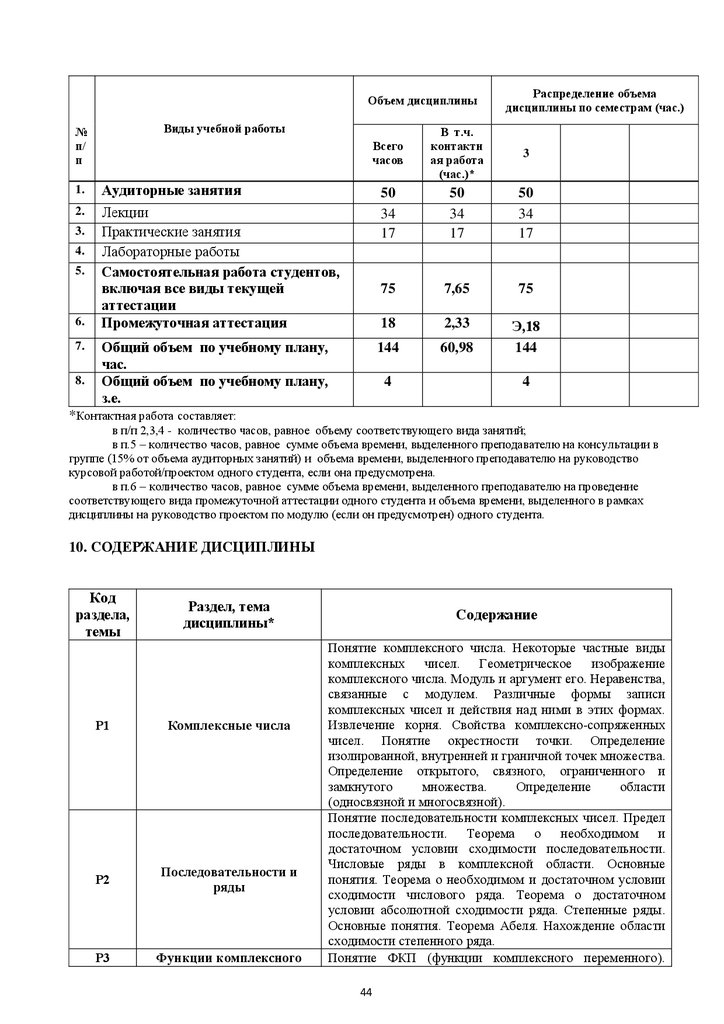
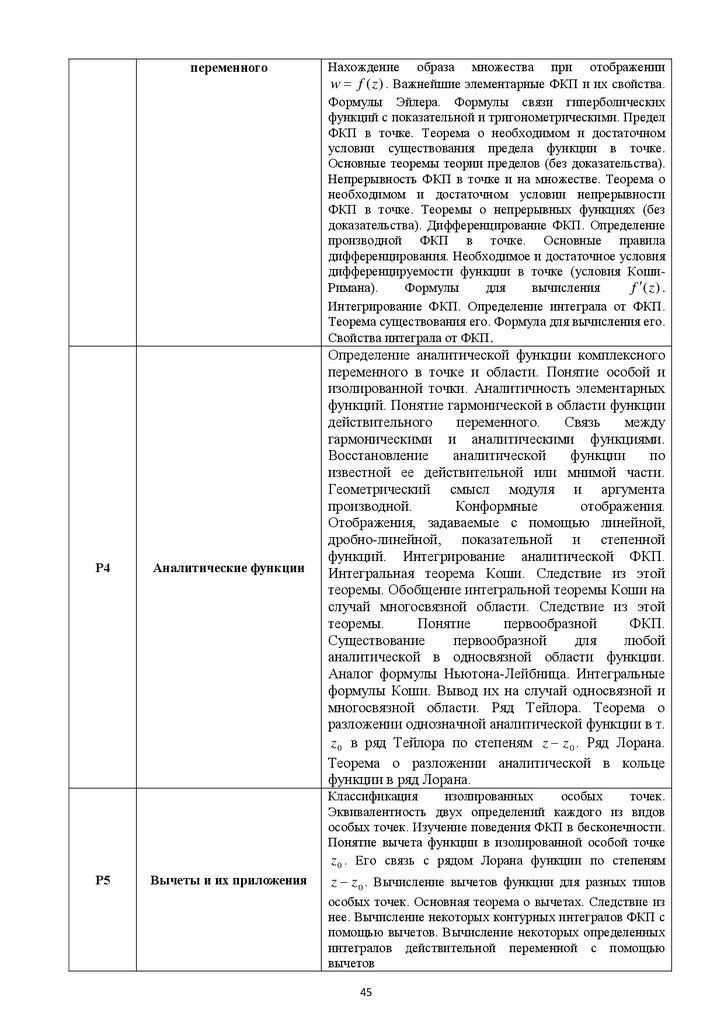

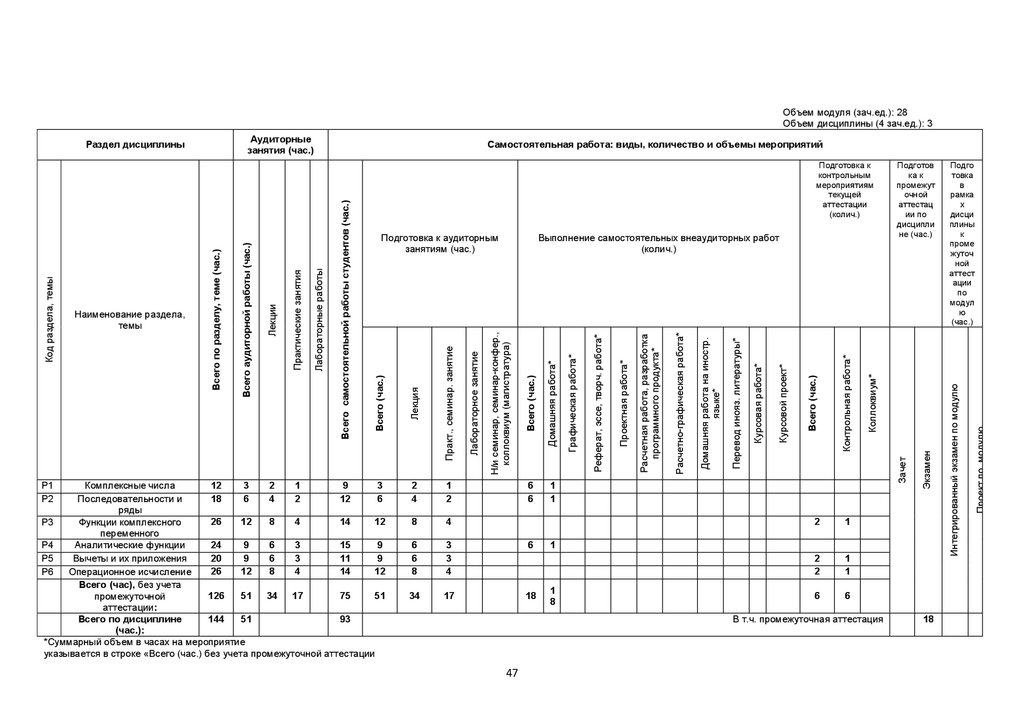



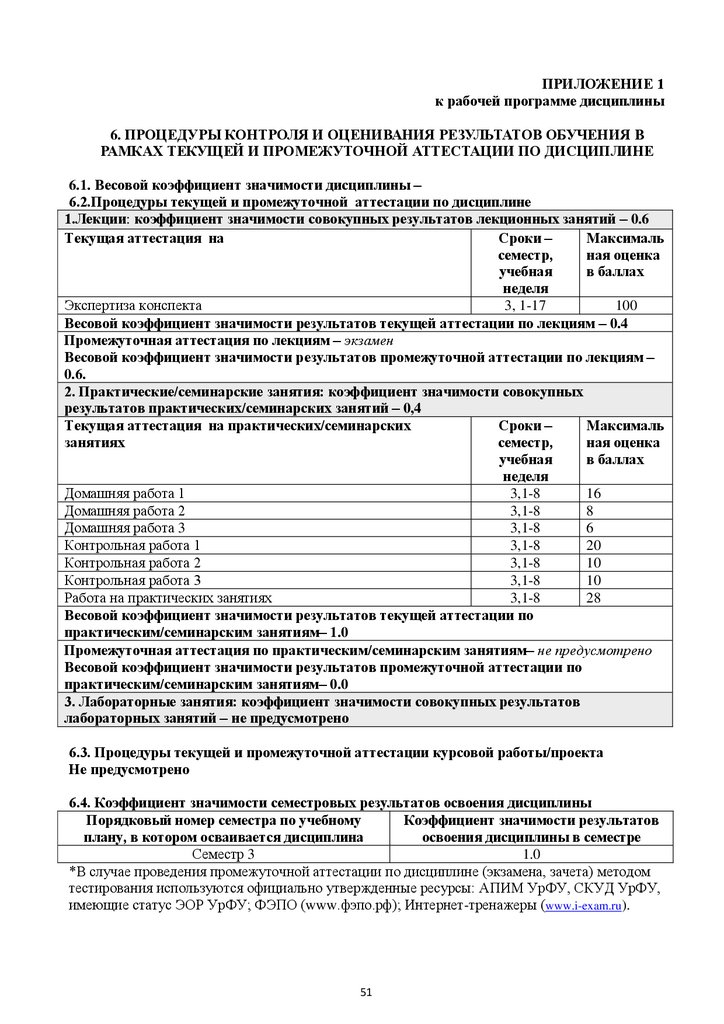

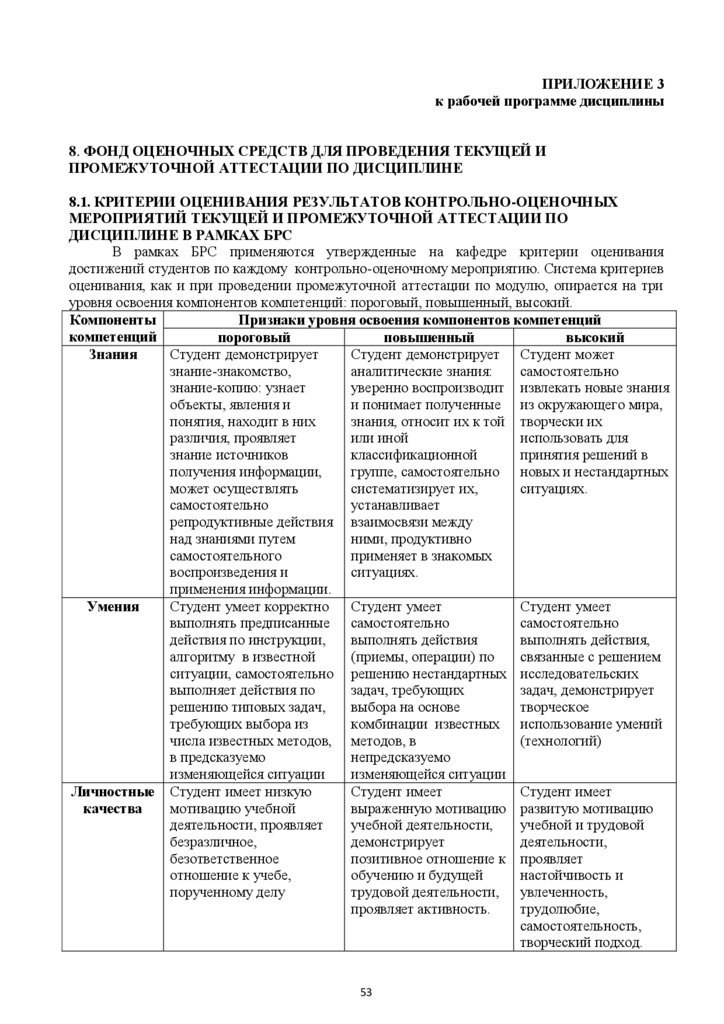






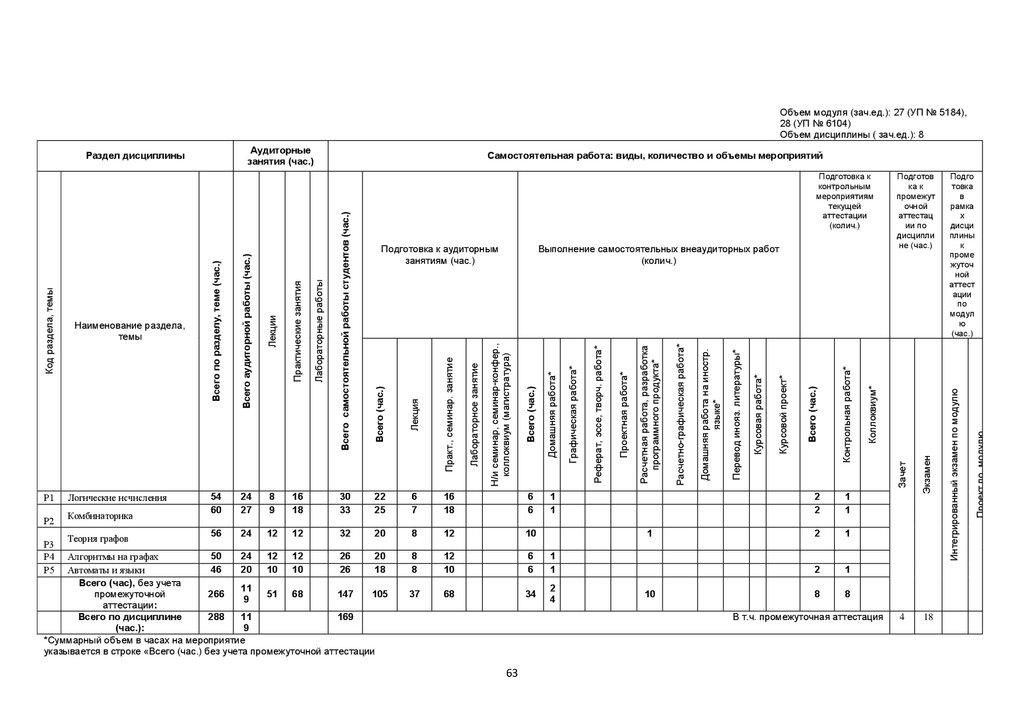












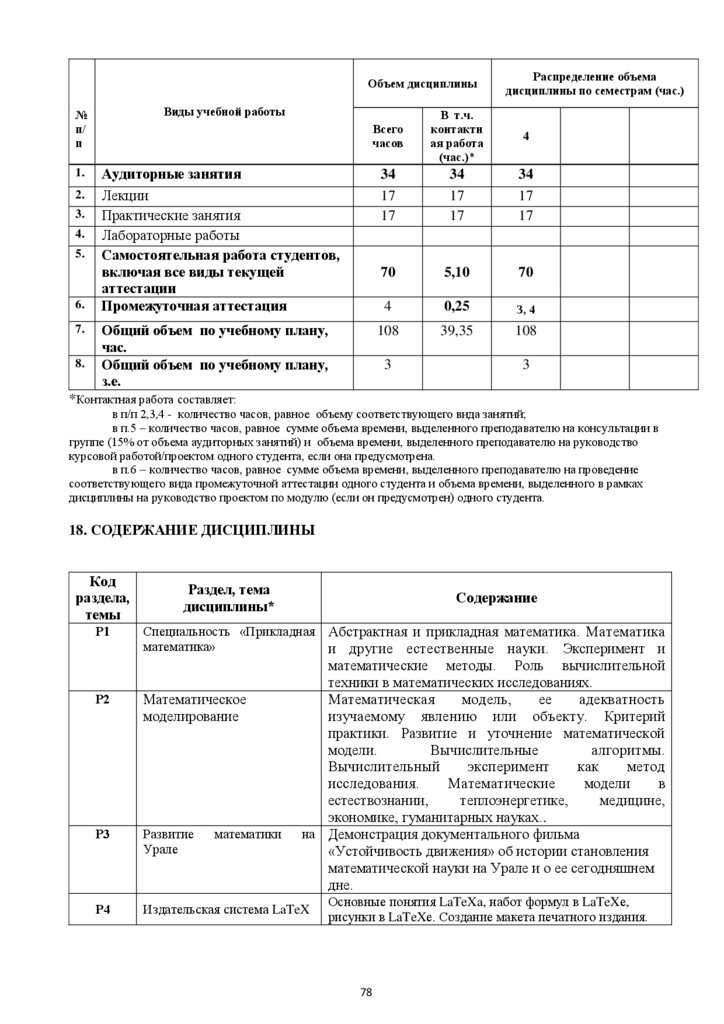

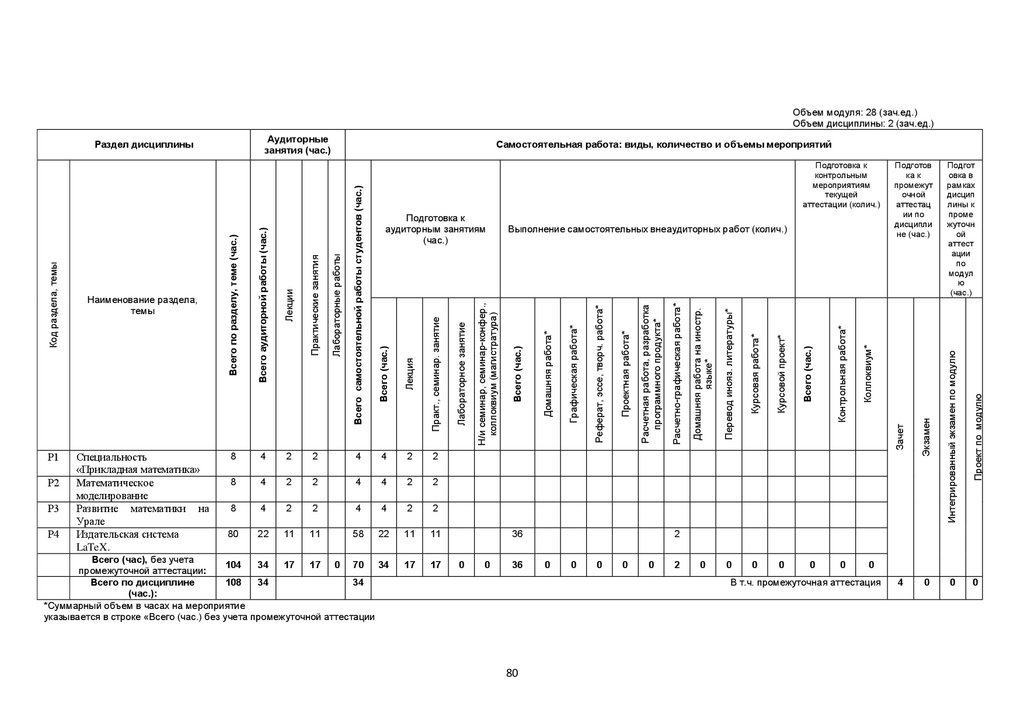





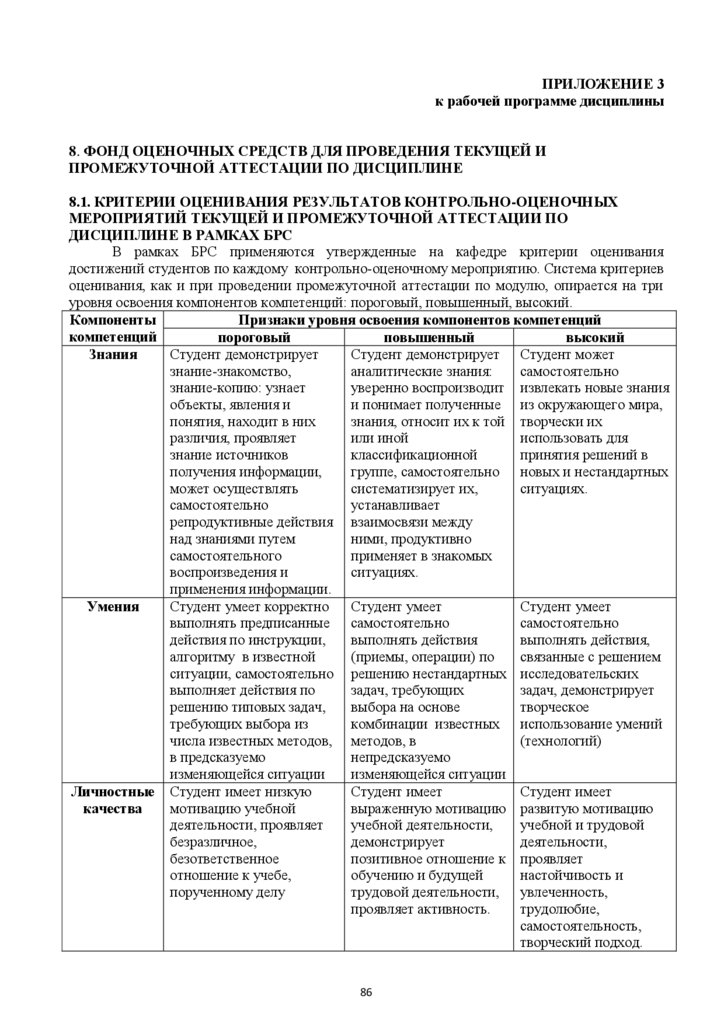








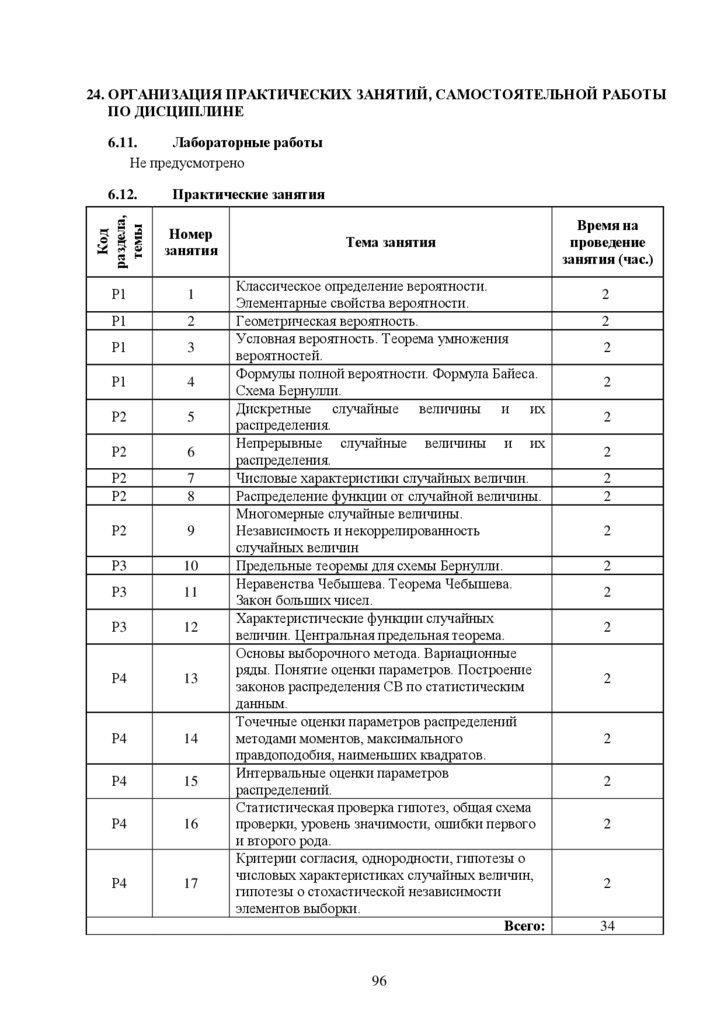





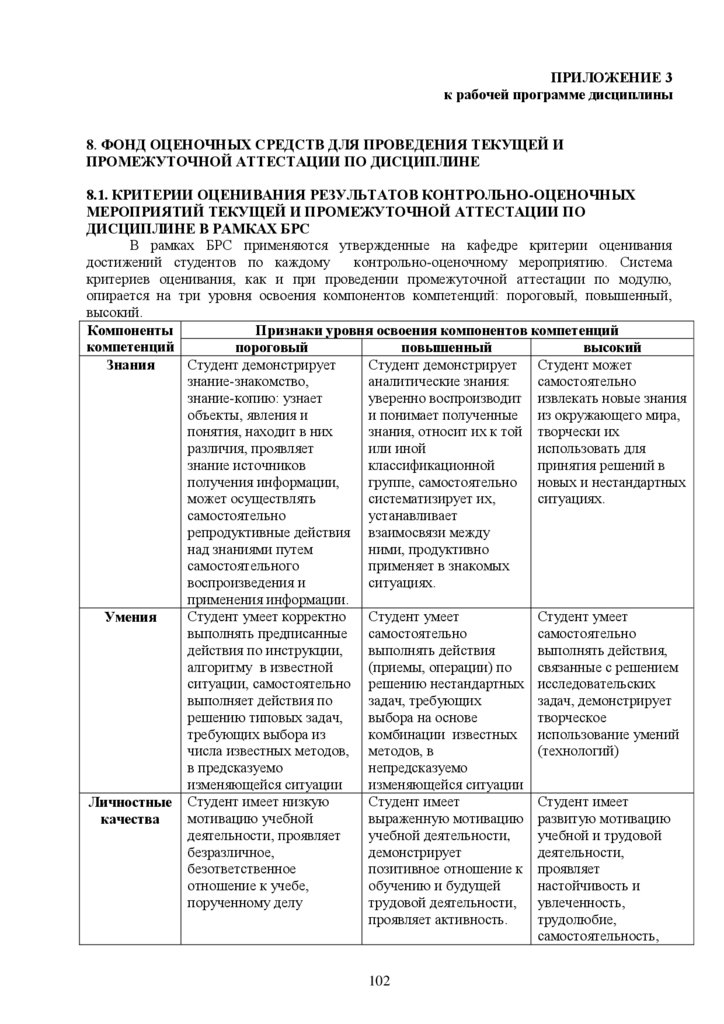



 Математика
Математика Образование
Образование





