Правильные многогранники

1. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

2. Симметрия в пространстве

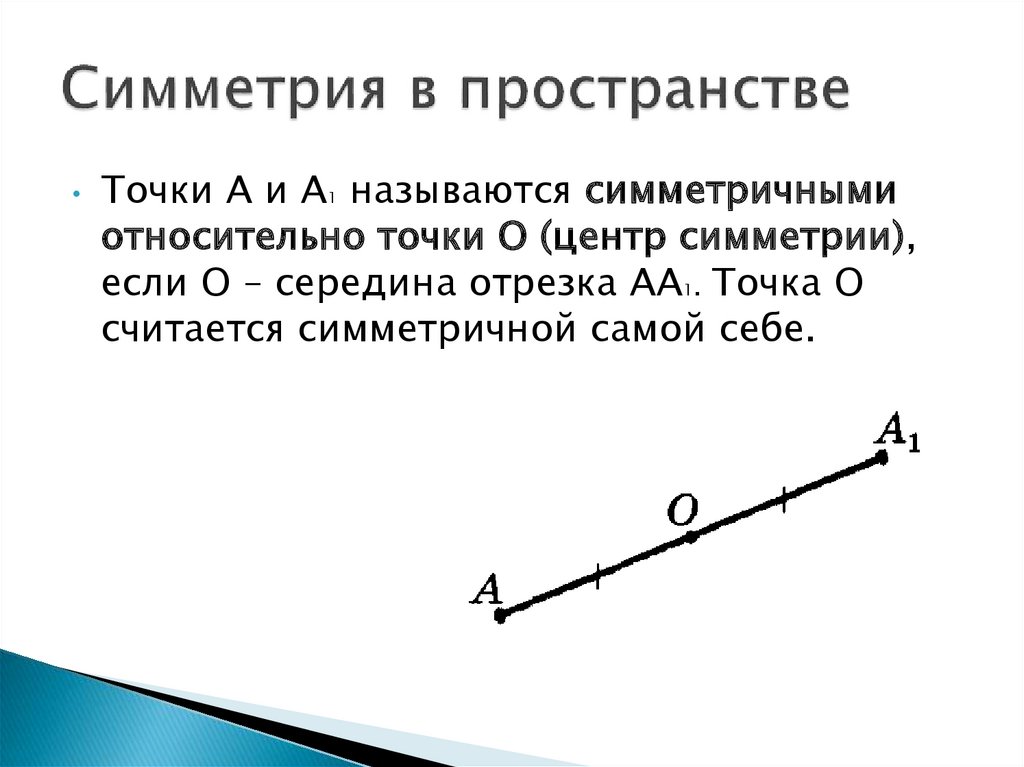
Точки А и А называются симметричными
относительно точки О (центр симметрии),
если О – середина отрезка АА1. Точка О
считается симметричной самой себе.
1

3.

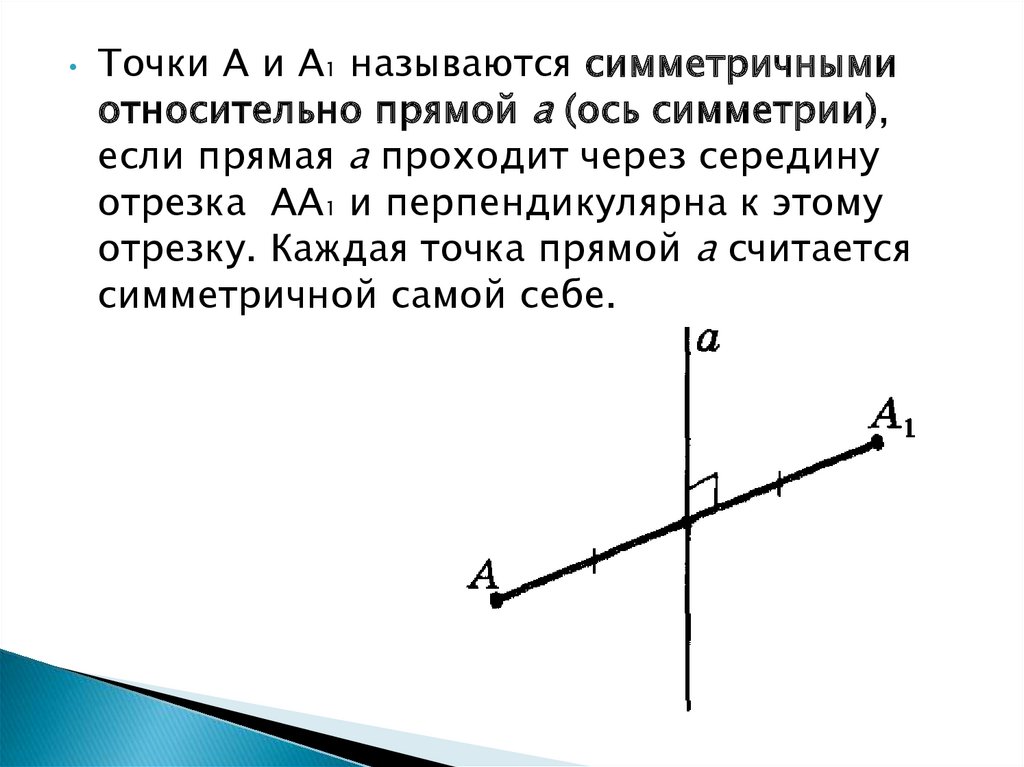
Точки А и А1 называются симметричными
относительно прямой а (ось симметрии),
если прямая а проходит через середину
отрезка АА1 и перпендикулярна к этому
отрезку. Каждая точка прямой а считается
симметричной самой себе.

4.

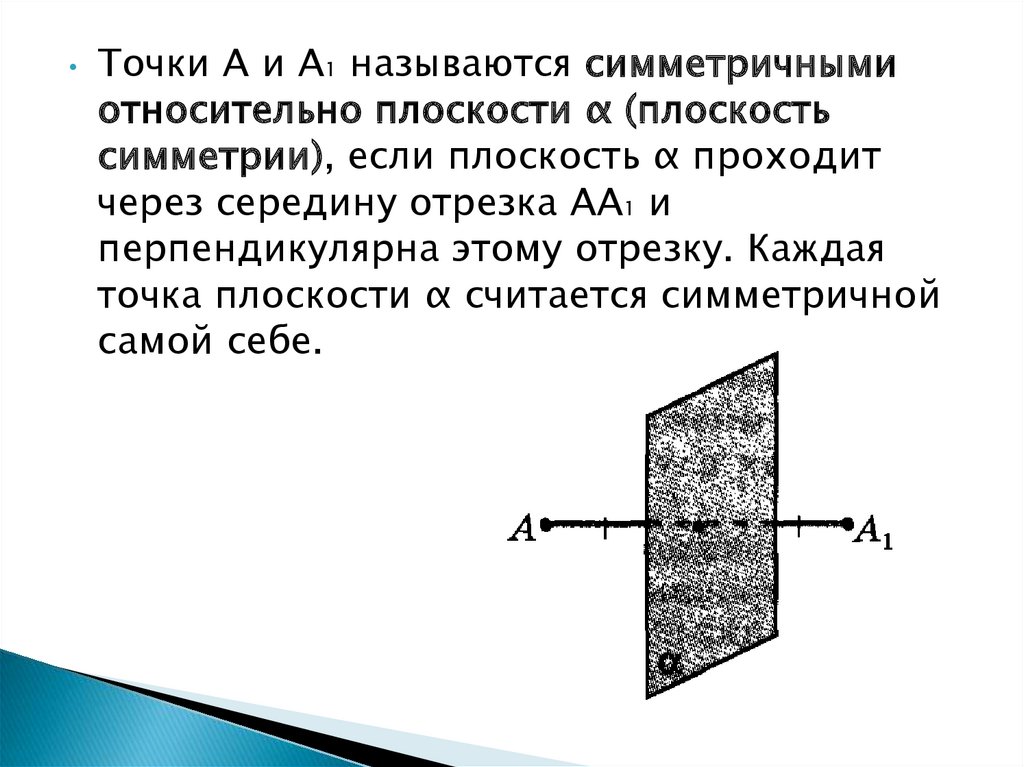
Точки А и А1 называются симметричными
относительно плоскости α (плоскость
симметрии), если плоскость α проходит
через середину отрезка АА1 и
перпендикулярна этому отрезку. Каждая
точка плоскости α считается симметричной
самой себе.

5. Понятие центра, оси и плоскости симметрии фигуры.

Точка (прямая, плоскость) называется
центром (осью, плоскостью) симметрии
фигуры, если каждая точка фигуры
симметрична относительно нее некоторой
точке той же фигуры.
Если фигура имеет центр (ось, плоскость
симметрии), то говорят, что она обладает
центральной (осевой, зеркальной)
симметрией.

6.

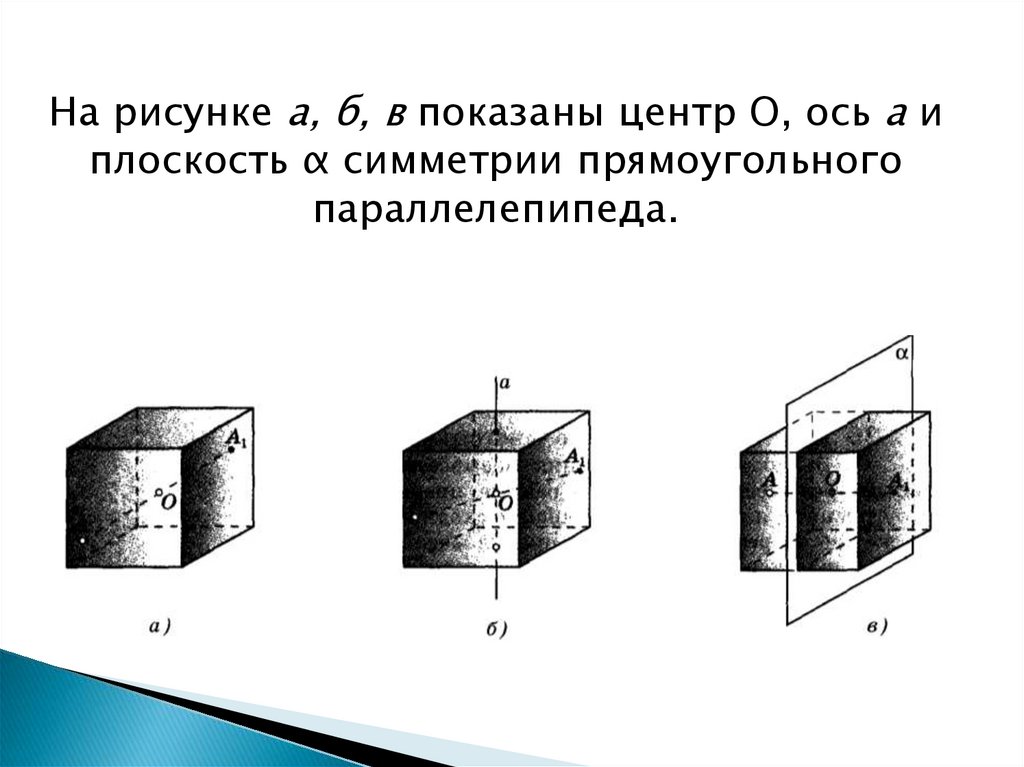
На рисунке а, б, в показаны центр О, ось а и
плоскость α симметрии прямоугольного
параллелепипеда.

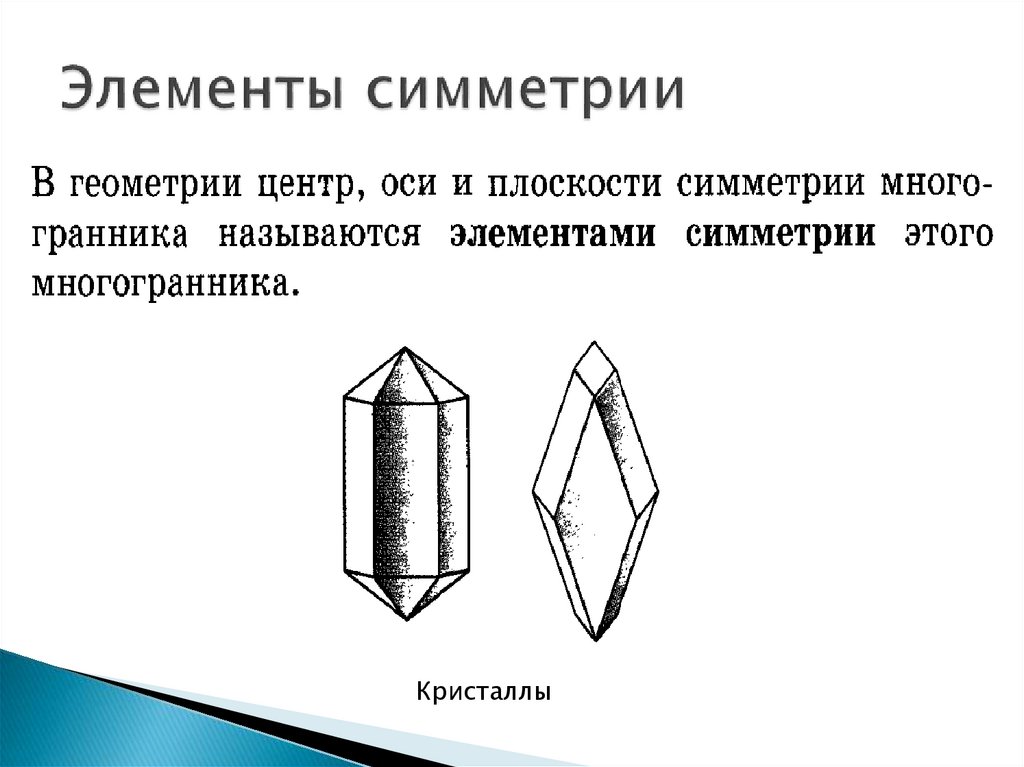
7. Элементы симметрии

Кристаллы

8. Понятие правильного многогранника

9. Правильные многогранники:

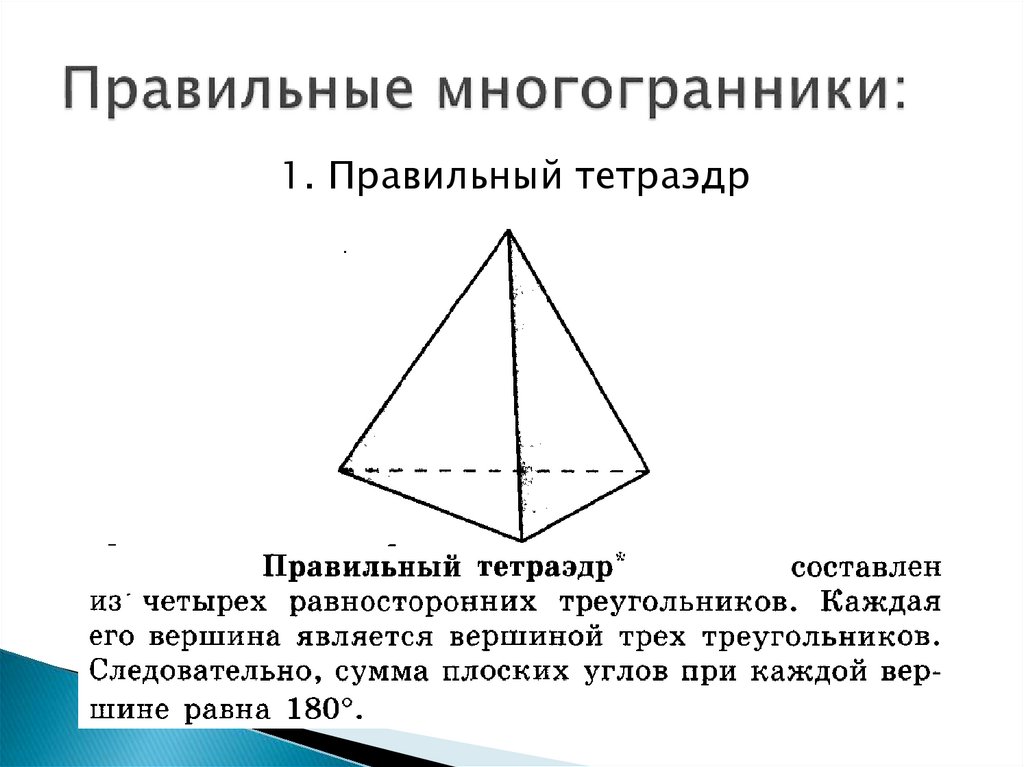
1. Правильный тетраэдр

10.

2. Правильный октаэдр

11.

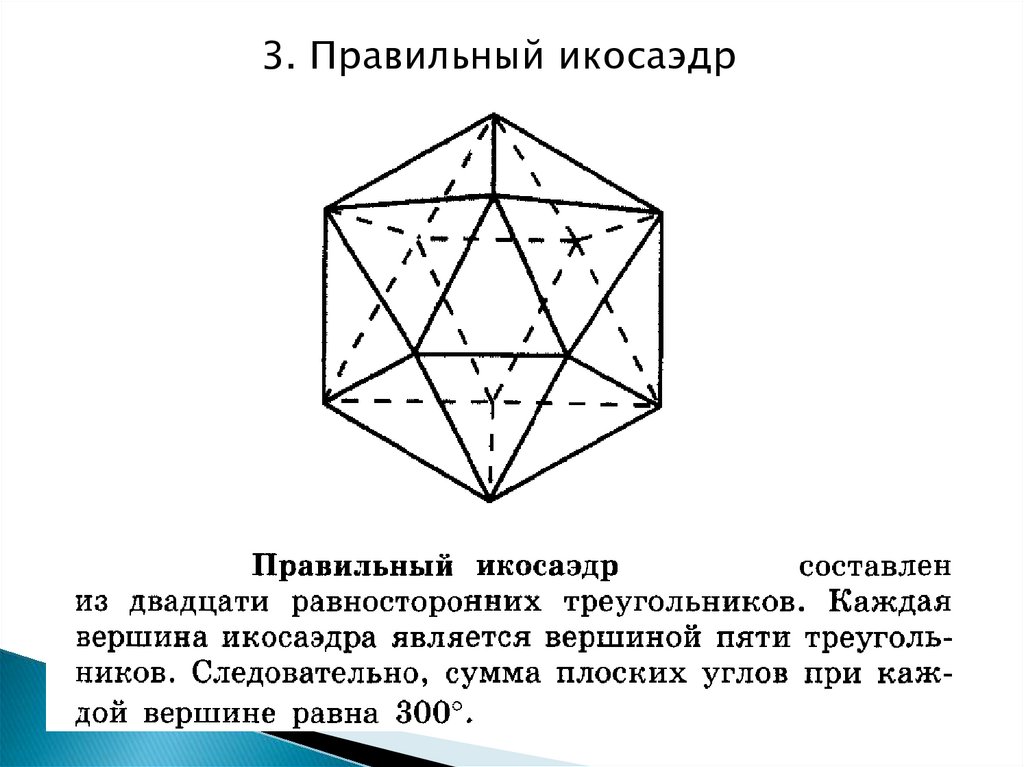
3. Правильный икосаэдр

12.

4. Куб

13.

5. Правильный додекаэдр

14. Элементы симметрии правильных многогранников.

Правильный тетраэдр не имеет центра
симметрии.
Правильный тетраэдр имеет три оси
симметрии и шесть плоскостей симметрии.

15.

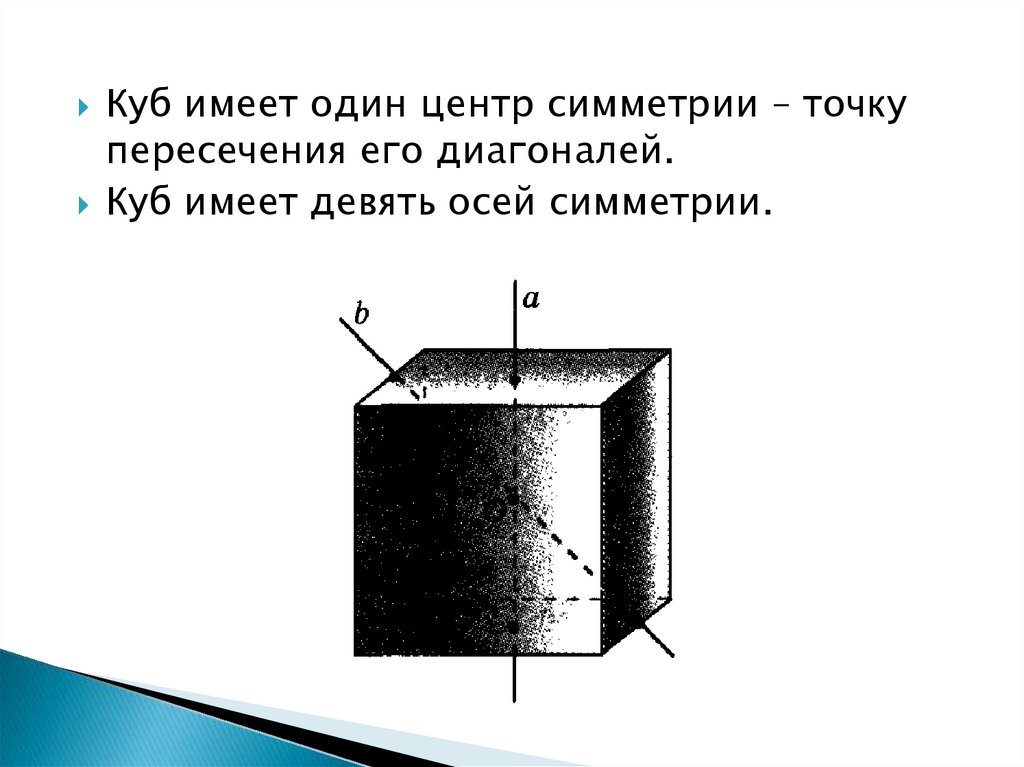
Куб имеет один центр симметрии – точку
пересечения его диагоналей.
Куб имеет девять осей симметрии.

16.

Правильный октаэдр, правильный икосаэдр
и правильный додекаэдр имеют центр
симметрии и несколько осей и плоскостей
симметрии.