Похожие презентации:
Системы счисления
1. Системы счисления
Составитель:учитель информатики
Семенихин И. Н.
МБОУ «СОШ № 56» г. Новокузнецк
2.
Системы счисления делятся на три вида:1.
2.
3.
Непозиционные системы счисления
Позиционные системы счисления
Смешанные системы счисления
3.
Непозиционная система счисления - этосистема счисления, в которой значение
цифры не изменяется в зависимости от
ее расположения.
4. Египетская система счисления
непозиционная система счисления, которая употреблялась вДревнем Египте вплоть до начала X века н.э. В этой системе
цифрами являлись иероглифические символы; они обозначали
числа 1 (черта), 10 (пятка), 100 (петля веревки), 1000 (кувшинка
или лотос), 10000 (палец), 100000 (жаба или личинка), 1000000
(человек с поднятыми вверх руками)
Числа, не кратные 10, записывались путем повторения этих цифр.
Каждая цифра могла повторяться от 1 до 9 раз.
5. Греческая система счисления
также известная как ионийская или новогреческая непозиционная система счисления, в которой, в качестве символовдля счёта, употребляют греческие буквы, а также дополнительные
символы, такие как ς (стигма), Ϙ (копа) и Ϡ (сампи).
Данные символы позволяют записать числа лишь от 1 до 999,
например:
45 — με
632 — χλβ
970 — Ϡο
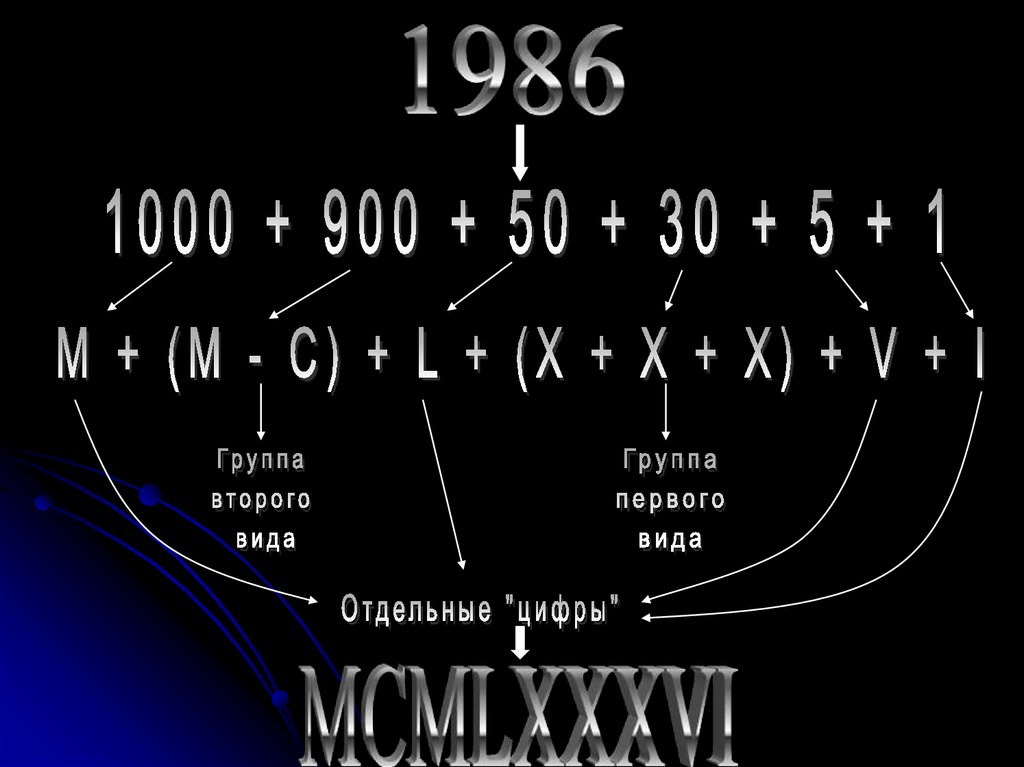
6. Римская система счисления
непозиционная система счисления, в которой для записи чиселиспользуются буквы латинского алфавита.
7.
8.
9. Немного о календаре Майя
Весь мир в курсе, что календарь Майя заканчивается21декабря 2012 года.
Но никто не знает почему.
Начнём с того, что на самом деле заканчивается не
календарь, а так называемый Великий цикл. Или
«Пятое Солнце» по терминологии майя
продолжительностью 5126 лет. Последний день этого
цикла - 21 декабря 2012 года. Но это не конец мира.
После 2012 года как бы начинается следующий цикл.
Согласно подсчетам ученых, «Пятое Солнце» началось
13 августа 3113 года до нашей эры. Почему именно
тогда? С каким событием это было связано? Никто не
знает. Равно как неизвестно, откуда у древних майя
вообще взялась их изощренная система счисления
времени и деления его на циклы.
10.
11.
Позиционная система счисления система счисления, в которой значениекаждого числового знака (цифры)
в записи числа зависит от его позиции
(разряда).
12.
1 — единичная (унарная) система счисления,может рассматриваться как вырожденный
случай позиционной системы счисления (счёт
на пальцах, зарубки, узелки «на память» и др.).
2 — двоичная система счисления
3 — троичная система счисления
4 — четверичная система счисления
7 — семеричная система счисления
8 — восьмеричная система счисления
10 — десятичная система счисления
12 — двенадцатеричная система счисления
16 — шестнадцатеричная система счисления
60 — шестидесятеричная система счисления
13.
Двоичная система числительных довольно широкораспространена среди языков Новой Гвинеи и
аборигенов Австралии.
Двоичные цифровые системы употреблялись для
гадания в древнем Китае и у народа йоруба в
Западной Африке.
Древнеегипетская система записи дробей "глаз
Гора" тоже была двоичной, поскольку шесть
частей глаза обозначали дроби в возрастающих
степенях двух: 1/2, 1/4, 1/8, 1/16, 1/32, 1/64.
Древние евреи считали пары жертвенных голубей
"гнездами" (киним), и этому виду
жертвоприношений посвящен специальный
трактат Мишны.
В современном мире, разумеется, двоичная
система записи цифр получила широчайшее
распространение благодаря компьютерной
технике.
14.
Числительные формируются по троичнойсистеме в языке вингей на Новой Гвинее, но
не последовательно, поскольку числами
третьего и четвертого порядка там служат 6 и
12, а не 9 и 27.
Троичная цифровая система была разработана
в древнем Китае на рубеже первого века до
н. э. и первого века н. э. как альтернатива
двоичной системе. Тетраграммами,
состоящими из трех знаков - горизонтальной
черты, черты с пробелом и черты с двумя
пробелами - можно записывать цифры до
256.
15.
Четверичная система числительных существовала в ныневымерших языках группы чумаш в Северной
Калифорнии.
В двух языках четверичная система последовательно
используется для формирования числительных более
высокого порядка: в языке каколи на Новой Гвинее и в
языке нгити в Северном Конго. В языке каколи после 48
четверичная система превращается в систему
исчисления на базе 24.
А в языке нгити четверичная система после 64 уступает
место системе на базе 32.
Обычай считать четверками широко распространен в
австронезийских языках. В Индонезии принято считать
"собаками" (асу) по числу ног, так что 200 свиней там
называются "50 собак".
Система летоисчисления по Олимпиадам, принятая в
Древней Греции, тоже была основана на четверичном
принципе, поскольку Олимпийские игры происходили
раз в четыре года.
16.
Семеричная система числительных нигде иникогда не употреблялась, но, несмотря на
это, семеричная система счета существует на
базе семидневной недели. Семь недель
между пасхой и праздником шавуот
составляют "счет снопов", которые каждый
день приносили в этот отрезок времени в
Иерусалимский храм. Один из еврейских
праздников называется лаг ба-омер - "33-ий
сноп", т. е. 33-ий день в этом счете, а в
христианской традиции сам праздник шавуот
называется "пятидесятница". Кроме того,
каждый седьмой год считается "субботним",
когда все сельскохозяйственные работы были
запрещены, а семь таких семилетий
составляли юбилей, когда долговых рабов
отпускали на волю и проводилась кассация
долгов.
17.
Восьмеричная система числительныхсуществовала в ныне мертвом языке юки в
южной Калифорнии и в языках группы паме в
северной Мексике.
В древнем Риме существовала восьмидневная
неделя - nundina. Слово это буквально значит
"девятка", и произошло это из-за того, что дни
недели римляне считали по системе
инклюзивного счета, по правилам которого
последний день предыдущей недели
одновременно считался первым днем
следующей недели. В результате, этот
последний день назывался "девятым", хотя
мы бы называли его восьмым.
18.
Десятичная система исчисления - самая распространенная в языкахмира. На десятичной основе строятся числительные большинства
индоевропейских (кроме кельтских), семито-хамитских, уралоалтайских, китайско-тибетских, австронезийских языков, языков
банту в Африке, кечуа и аймара в Южной Америке, на-дене и
алгонкинских в Северной Америке и многих других языков. До
самых высоких порядков счет по десятичной системе доходит в
микронезийских и в некоторых полинезийских языках, где он
использовался для подсчета кокосовых орехов. В микронезийском
языке нукуоро счет доходит до 10.000.000.000!
Nukuoro
10 hulu
100 lau
1.000 mano
10.000 (se)mada
100.000 (se)guli
1.000.000 (se)loo
10.000.000 (se)ngaa
100.000.000 (se)muna
1.000.000.000 (se)bugi
10.000.000.000 (se)baga
19.
Двенадцатеричная система в современных английском инемецком языках, возникла, по-видимому, под влиянием
обычая считать "дюжинами". Третий порядок называется в
этом счете гросс (144), а четвертый - масса (1728). Сам же
этот обычай возник, по всей видимости, на базе
двенадцатеричного характера большинства европейских
единиц измерения. Произошло это, в свою очередь, из-за
удобства такого счета для всевозможных ежемесячных
платежей. Так, например, римская унция значила в числе
прочего 1/12%, т. е. учетную ставку в 1% годовых. Эта унция
также лежала в основе римской системы записи дробей, в
которой точкой обозначалась 1/12, а половина - буквой S.
На двенадцатеричной системе основано деление суток на 24
часа: 12 часов дня и 12 часов ночи. С изобретением
механических часов эти отрезки времени стали равными, но
римский час, принятый и в Средние Века, был длиннее
летом и короче зимой, в зависимости от продолжительности
дня от рассвета до заката.
20.
На системе счета по частям тела построенашестнадцатеричная система числительных у
австралийских аборигенов вурунджери.
По шестнадцатеричной системе строятся и
числительные первого порядка в
современном французском языке.
Широко используется в низкоуровневом
программировании и компьютерной
документации. Обычно в
качестве шестнадцатеричных
цифр используются десятичные цифры от 0
до 9 и латинские буквы от A до F для
обозначения цифр от 10 до 15 , то есть (0, 1,
2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
10
10
21.
Исторический интерес представляет такназываемая «вавилонская», или
шестидесятеричная система счисления,
весьма сложная, существовавшая в Древнем
Вавилоне, за две тысячи лет до н.э. Это
первая известная нам система счисления,
основанная на позиционном принципе.
Система вавилонян сыграла большую роль в
развитии математики и астрономии, ее следы
сохранились до наших дней. Так, мы до сих
пор делим час на 60 минут, а минуту на 60
секунд. Точно так же, следуя примеру
вавилонян, окружность мы делим на 360
частей (градусов).
22. Смешанные системы счисления
Фибоначчиева система счисления —смешанная система счисления для
целых чисел на основе чисел
Фибоначчи F2=1, F3=2, F4=3, F5=5,
F6=8 и т.д.
В факториальной системе
счисления основаниями являются
последовательность факториалов
23. Практическое задание
1.2.
3.
Запишите в египетской системе
счисления числа: 13, 76, 148.
Запишите в греческой системе
счисления числа: 19, 95, 682, 874.
Запишите в римской системе
счисления числа: 951, 3279, 5164,
8468.






















 Информатика
Информатика








