Формализация задачи обобщенного оценивания состояния динамических систем
1.
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГООБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН
ТАШКЕНТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ ИМЕНИ АБУ РАЙХАНА БЕРУНИ
АБДУРАХМАНОВА Юлдуз Мухтарходжаевна
РЕГУЛЯРИЗОВАННЫЕ АЛГОРИТМЫ
ОБОБЩЕННОГО ОЦЕНИВАНИЯ
ДИНАМИЧЕСКИХ СИСТЕМ
Ташкент - 2010
2.
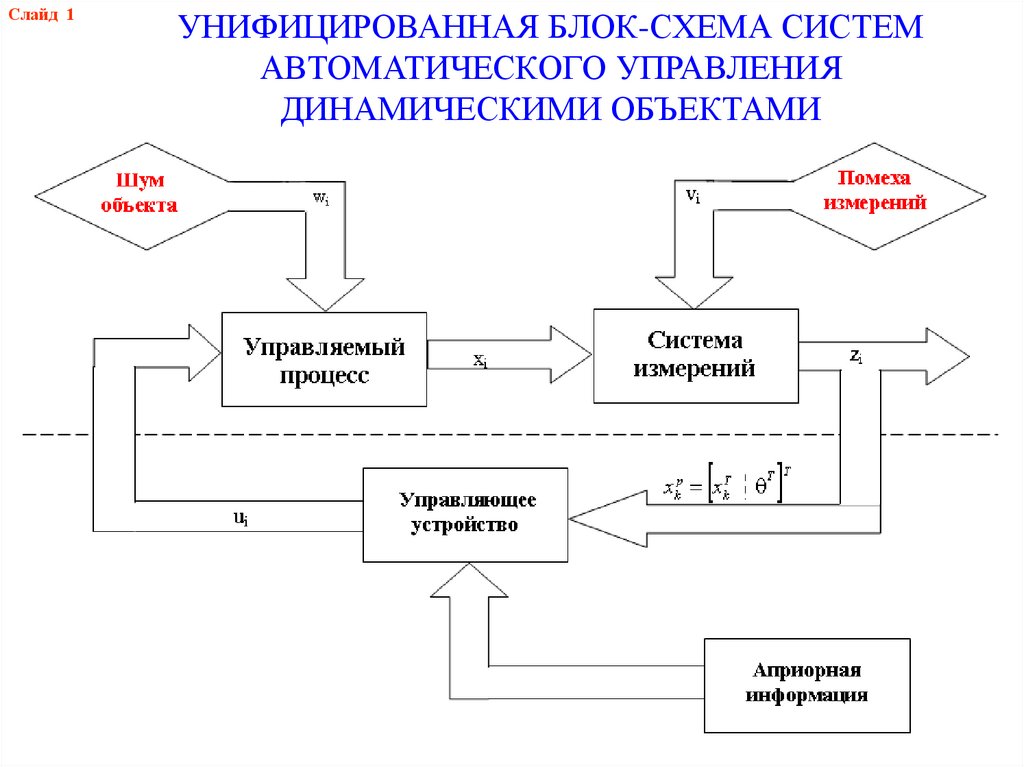
Слайд 1УНИФИЦИРОВАННАЯ БЛОК-СХЕМА СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
ДИНАМИЧЕСКИМИ ОБЪЕКТАМИ
3.
Слайд 2ФОРМАЛИЗАЦИЯ ЗАДАЧИ ОБОБЩЕННОГО ОЦЕНИВАНИЯ
СОСТОЯНИЯ ДИНАМИЧЕСКИХ СИСТЕМ
xk 1 F ( k , )xk wk , zk H ( k , )xk vk ,
xkp [ xkT
T ] T , x kp 1 f p ( x kp , k ) g p ( x kp , k ) wk , z k h p ( xkp , k ) vk ,
f p ( xkp , k ) xkT F T ( k , ) 0
x̂( k | k ,k 0 ) [ I
T
,
g( xkp , k ) GT ( k , ) 0
T
,
0 ] x̂ p ( k | k ,k 0 ) ;
xk 1 ( k 1, k , )xk G ( k , )uk wk zk H ( k , )xk vk , 1,2,..., n ,
,
xk 1 p (k 1, k , p ) xkp G p (k , p )uk wk
,
zk H p ( k , p )xkp vk , 1,2,..., n,
wk [ w1T ( k ) w2T ...wnT ( k )] T , xkp [ x1T ( k ) ...xnT ( k )] T ,
a [ ... ]
T
1
T
2
T
n
n
T
,
H p ( k , p ) H ( k , ) ;
1
xkp 1
f [ xkp , k ] p g[ xkp , k ]
I
p
x
u
k
k wk , z k h[ xk , k ] vk ,
0
0
0
h[ xkp , k ] H (k , ) xk , f [ xkp , k ] (k 1, k ; ) xk , g [ xk ,k ] H ( k , )xk
p
.
4.
РЕГУЛЯРИЗОВАННЫЕ АЛГОРИТМЫ ОБОБЩЕННОГООЦЕНИВАНИЯ НЕЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ ПРИ
НАЛИЧИИ ОШИБОК В МОДЕЛИ ОБЪЕКТА УПРАВЛЕНИЯ
Слайд 3
xk Fk ( xk 1 , uk 1 )
(k 1, 2, ... ) , xk ( x1k , xk2 , ...., xkn ) , Fk ( Fk1 , Fk2 , ... , Fkn )
z k z k ( xk , vk )
(k 1, 2, ...) , z k ( z 1k , z k2 , ...., z kn )
u k u k ( x̂k ) , x̂k x̂k / k 1 K k ( yk ẑ k / k 1 ) .
x̂k / k 1 x̂k / k 1 ( x̂k / k 1 ,u k 1 ) , ẑ k / k 1 ẑ k / k 1 ( x̂k 1 ,u k 1 )
xk Fk ( xk 1 , uk 1 ) ,
Fk ( Fk 1 , Fk 2 , ... , Fk n ) , z i z i ( xi , vi ) .
zk Ek ( x̂k / k 1 ) H k xk Lk vk ,
xk k ( x̂k 1 , uk 1 ) Ck xk 1 ,
k ( x̂k 1 ,uk 1 ) Fk* ( x̂k 1 ,uk 1 ) Ck x̂k 1 , Ek ( x̂k / k 1 ) z*k ( x̂k / k 1 , vk 0 ) H k xk / k 1 ,
m
m
s
s
st st
st min M ( xk x̂k / k 1 ) 2 k k k k kst1 k kst tk1t ,
kk ( t 1,2 ,... ,m )
t 1
t1 ,t 1
s
k
m
k
t1 1
stk (t 1, 2, ... , m; s 1, 2, ... , n) Kk k k (k 1, 2, ... )
st t1t
k k
,
K k k Г k Z I Г k Г k
,
Г k lim Г k I
0
1
,
0
,
;
kkj,r kkj,r 1 g Г kT Г kT kkj,r 1 kj , r 1,2,... , g Г kT Г kT I ,
~
~
~
1
g , 0 , kk j,r kk j,r 1 g Г kT Г kT kk j,r 1 kj wk ,r , r 1,2,... , wk ,r ,
r
~
k k j,r k*j I Г kT g r Г kT k0j k*j r .
1
5.
Слайд 4ОЦЕНИВАНИЕ ОБОБЩЕННОГО ВЕКТОРА СОСТОЯНИЯ
НА ОСНОВЕ ПРИНЦИПА РЕГУЛЯРИЗАЦИИ
1
J h( k 1 ) z x
2
h( k 1 ) z x ( k 1 ), k 1 ,
x p (k 1) x р (k ), k B x p (k ), k w(k ) , h( k ) z x p ( k ), k ( k ) ,
kr 1
k k0
J
p
T
( k 1 ), k 1 V 1
p
T
1 p
x̂ ( k 0 ) x p ( k ) V0 1 x̂ p ( k 0 ) x p ( k 0 )
2
T
1 ku 1
p
h( k 1 ) z x̂ ( k 1 ), k 1 V 1 h( k 1 ) z x̂ p ( k 1 ), k 1
2 k k0
k r 1
T 1
1 kr 1 p
1 kr 1
p
p
p
T
1
x̂ ( k ) x ( k ) Vx x̂ ( k ) x ( k ) ŵ( k ) Vw ŵ( k ) T ( k 1 )
2 k k0
2 k k0
k k0
h( k ) z x̂ ( k ), k w x̂ ( k ) , , w w ,
z x̂ ( k 1 ), k 1
x̂ ( k 1 ) x̂ ( k ), k P( k 1 ){
V ( k 1 )[ h( k 1 )
x̂ ( k 1 )
x̂ p ( k ), k B x̂ p ( k ), k ŵ( k ) x̂ p ( k 1 ) , 0,
p
0
2
k
0
T
p
1
p
p
p
p
0
k
0
1
z [ x̂ p ( k 1 ), k 1]] Vx 1 [ x̂ p ( k 1 ) x p ( k 1 )]} ,
M [ x̂ p ( k 1 ), k 1]
1
1
P( k 1 ) { I
P
(
k
1
k
)
V
P
(
k
1
k
)}
P( k 1 k ) .
x
p
x̂ ( k 1 )
6.
АЛГОРИТМЫ ОБОБЩЕННОГО ОЦЕНИВАНИЯДИНАМИЧЕСКИХ СИСТЕМ В СИТУАЦИИ НЕОПРЕДЕЛЕННОСТИ
Слайд 5
z i f ( xi0 ), x00 x00 , A0 A A ,
xi0 1 f ( xi0 , u i0 , A 0 , k i ) ,
xi0 1 f ( xi0 ,ui0 , A0 ,k i ) b f ( xi0 ,ui0 , A0 , A,k i ) ,
x1,i 1 f1( xi , ui , A, ki ) bX i , z ip h( xi0 , i ) vi , 0 i N 1 , x3,i 1,k f 2 ( x3i ,k ,ui0 , w2i ,k , ki ) ,
x3i , k
x2i , k
i ,k
;
f 1 ( x 2i ,k , u i0 , A, k i ) bX i ,k
f 2 ( x3i ,k , u i0 , w2i ,k , k i ) dw2i ,k ;
i, k
0
d t ,
E
k
F2 (i, k ) 1
F2 (0, k ) 1
z
2
p
i
z
2
2 k F2 (i, k ), 0 k N 1 ,
p
i
T
i 0
h2 ( x3i ,k , i ) Vi 1 z ip h2 ( x3i ,k , i ) w2Ti ,k Q2i w2i ,k
T
T
1
h2 ( x3( 0), k ,0) V0 1 z ip h2 ( x30, k ,0) w20
, k Q20 w20, k
h2 ( x3i ,k ,i ) h( x2i ,k , X 0,i ); x30
x
2
0 k N 1 ,
x30,k M 20 x30 x30,k
T
30
x 00
;
0
x̂3k ,k x̂3k ,k 1 M 2 k h2Ts x̂3k ,k 1 ,tk Vk 1 zkp h2 ( x̂3k ,k 1 ,tk ) ,
x̂3k ,k 1 f 2 ( x̂3k 1,k 1 ,ui0 1 , ŵ2 k 1,k 1 0, k 1 ) ,
1
M 2k F2 s (k , k 1) M 2 k1,k 1 k E , k k 1 , k 1,2,..., ,
M 2 k ,k 1 f 2 s ( k 1, k 1 )M 2 ,r 1 f 2Ts ( k 1, k 1 ) dQ2 ,1k 1d T .
7.
Слайд 6АЛГОРИТМЫ ОЦЕНИВАНИЯ ВЕКТОРА ВОЗМУЩЕНИЙ
В ЗАДАЧАХ ОБОБЩЕННОЙ ФИЛЬТРАЦИИ
x kp f k ( x kp , u k 1 , w(k )), k 1,2,... ,
N1
( n) , n 1,2,...N : w( k ) ( n )qn ( k ) , k 1,2,... , w ( (1) , ( 2) ... ( N ) ) .
1
n 1
z k f k ( x kp , W (k )), k 1,2,... ,
N2
W ( k ) W ( n )qn ( k ) W (W (1) , W ( 2) ,...W ( N 2 ) ) ,
n 1
N
V̂ arg min J 0 ( V ) arg min bnV 2 , V ( xkp , wk ) ,
v I
V I
n 1
~
V Sp( B ee T ), e z z 0 , V min V J 0 V , 1,,
V
N
( V ) a V
n 1
n n
N
n ( V n )2 ,a 0, 1,
n 1
Vr 1 PQ Vr r ' ( Vr ) rVr ,
r ( 1 r ) 1 / 2 , r ( 1 r ) p , 0 p 1 .
8.
Слайд 7РЕГУЛЯРИЗОВАННЫЕ АЛГОРИТМЫ КОРРЕКЦИИ РЕЗУЛЬТАТОВ
ОБОБЩЕННОГО ОЦЕНИВАНИЯ СОСТОЯНИЯ И ПАРАМЕТРОВ
x kp 1 f k (k , x kp , u k , k ), k [k 0 , T ] , z k g k (k , x kp , d k , k ) , z zk R n ,
T T
X̂ k 1 FkX ( k , X k , z k ,Vk , K k ), K k 1 FkK ( k , X k , z k ,Vk , K k ), X k [ xk , yk ] T ,k [ k0 ,T ] ,
(k , xk* , uk , c) 0 k [k0 , T ] ,
x* p x x p x ,
(k , xk* , uk , c ) c (k ), c (k ) k [k0 , T ] ,
( k , x*k p ,u k ,c ) ( k , x̂kp ,u k ,c ) , ( k , x*k p ,u k ,c ) ( k , x̂kp ,u k ,c ) ,
1
s min ( s ) min ( k , x̂
k
{s}
4
{s}
s ,c min ( s ,c
k
{ s ,c }
p
k
2
sk ,u k ,c ) ;
2
p
,
)
min
(
k
,
x̂
k s k ,u k ,c )
5
{ s ,c }
( D) H T ( D) H ( D) ,
H ( D ) [ H i ( D ), i 1, n0 N ] T [ hi [ x̂kp0 , D ],...,hi [ x̂kpN 1 , D ], i 1, n0 ] T ,
( D)
T
( D) H ( D) 0 ,
D
( D) H ( D) / D [ H i ( D) / D j , i 1, n0 N , j 1, l ] ,
1 T
T
D( j ) D( j 1) j ( j 1) ( j 1) j I ( j 1) H ( D( j 1) ), j 1, J 0 ,
1 T
T
D( j ) D( j 1) j ( j 1) ( j 1) j Г j ( j 1) H ( D( j 1) ),
Г j diag (Tj 1) ( j 1) , j B( j 1) 1 , B 0 .
9.
РЕГУЛЯРНОЕ ОЦЕНИВАНИЕ ОБОБЩЕННОГО СОСТОЯНИЯДИНАМИЧЕСКИХ СИСТЕМ АСИМПТОТИЧЕСКИМ МЕТОДОМ
Слайд 8
x kp 1 f ( x kp , k ) G ( x kp , k ) wk ,
z k y ( x kp , k ) v k ,
k [0, k N ],
mw
mn
a je cos( je ); Vnj ( ) exp bie cos( ki ),
Vwj ( ) exp
n k 1
w e 1
j ( ) Vwj ( ) exp( / w ); nj ( ) Vnj ( ) exp( / n ) ,
yw
yv
w jk ẑ je( k ) o( ), k ,k N , vik q̂il ( k ) o( 2 ), k ,k N , o( ) ,
2
e 1
l 1
ẑ je( k ) 1 2w 2je
0.5
je( k ) ,
q̂ik ( k ) 1 2n ik2
0.5
ik ( k ) ,
x̂kp 1 f ( x̂kp , k ) K ( x̂kp , k )[ z k y( x̂kp , k )],
K ( x̂k ,k ) Vx ( k )H ( x̂k ,k )T N 1 ,
Vx ( k 1 ) F ( x̂k , k )Vx ( k ) Vx ( k )F ( x̂k ,k )T
Vx ( k )H ( x̂k , k )T N 1H ( x̂k , k )T Vx ( k ) G( x̂k ,k )RG( x̂k ,k )T .
10.
РЕГУЛЯРНОЕ ОЦЕНИВАНИЕ ВЕКТОРА СОСТОЯНИЯ ИПАРАМЕТРОВ НА ОСНОВЕ МЕТОДА КВАЗИЛИНЕАРИЗАЦИИ
Слайд 9
xk 1 f [ xk , k ] wk ,
zk h[ xk , k ] vk ,
E wk wTj Qk k j , E vk vTj Rk k j ,
i 1
kj
z C x
'
kj
i
kj
m
J z k j h x̂ ,k j
j 1
M
i 1
m
CQC
j 1
i 1 T
kj
i 1
k
T
kj
kj
i
kj
x̂
h [ x̂ki ,k j ]
x̂ki
i 1
kj
x̂
i
kj
i
kj
2
i
kj
i
kj
h [ x̂ki , k j ]
x̂ ki
m
2
j 1
Rk j
z 'k j Cki j x̂ki j 1
kj
i 1
kj
, N ik 1 T CkT Qk zk Ck pki 1 , x̂ki 1 ik 1 x̂ki 1 pki 1 ,
m
i 1
j 1
j
j
j
j
j
0
j
f [ x̂ki ,k ] i 1
f [ x̂ki , k ] i
i 1
i 1
i
k , k0 I , p k f [ x̂k , k ]
x̂k pki 1
i
i
x̂k
x̂k
G x̂ r M x̂
, x̂
G x̂ G x̂
r
r
i 1
k0
.
M i 1 x̂ki 0 1 N i 1 ,
2
G x̂ki 0 1 M i 1 x̂ki 0 1 N i 1
x̂ki 01 X
i
kj
Rk j
x̂ki 0 1 M i 1 I
inf
j 1,2,..., m , z zk j h x̂ , k j C x̂ , C
vk j ,
'
kj
i 1
k0
r
i 1 i 1
k0
i 1 r
k0
ri 1, 1 ri 1,
1
N i 1 .
x̂ki 0 1 , >0.
2
2
2
N i 1 x̂ki 0 1 , r 0 , 1 r
i 1( r )
k0
( )
x̂ki 0 1
r
, 0 ( r ) M i 1 x̂ki 1 N i 1 ,
0 (ri 1, )( 0 (ri 1, ))
, 0,1,....,
0 (ri 1, )
0
11.
АЛГОРИТМЫ ОБОБЩЕННОГО ОЦЕНИВАНИЯНА ОСНОВЕ КУСОЧНО- ГАУССОВСКОЙ АППРОКСИМАЦИИ
АПОСТЕРИОРНОЙ ПЛОТНОСТИ
Слайд 10
k 1 k , x kp k ( ) k x kp wk , z k k ( ) H k x kp Vk , k 1,2...
j
j
j
k ( ) k ( kj ) kj ( kj ) , k ( ) k ( k ) k ( k ) ,
~j
~ j~ j
~
j
j
~
~
j j ,
x̂i x̂i / i 1 Ki ( yi H i x̂i / i 1 i ( ij ) ij ij ) , ~
x̂i j/ i 1 ij ~
x̂i 1 i ( ij )
i i
M
ˆ
i
j 1 j
M
~
j~j
~
~
N ( xi , x̂i Pi )d dxi , x̂i xi ij N j ( ~
xi , ~
x̂i j Pi j )d dxi ,
j
i
j
j 1 j
bi j f j ( / Yi )d ,
j
M
M
ˆ b , x̂ x̂ j j ( P x ) j ( P xj ) 1 b j .
i i i
i
i
i
i
j 1
j j
i i
j 1
12.
Слайд 11РЕГУЛЯРНЫЕ АЛГОРИТМЫ НА ОСНОВЕ ОБОБЩЕННОГО
РАЗДЕЛЕННОГО ОЦЕНИВАНИЯ
xk 1 Fk ( xk , , wk ), k 0,1,2,..., x(0) x0 ,
z k Gk ( x k , , v k ), k 0,1,2,..., z (0) z 0 ,
x̂k E( xk | z k ) , Pk E ( x̂k xk )( x̂k xk )T | z k , p( 1 | z k ),..., p( N | z k ) ,
N
N
x̂k x̂k ( i ) p( i | z ) , Pk Pk ( i ) x̂k ( i ) x̂k x̂k ( i ) x̂k p( i | z k ) ,
k
i 1
i 1
p( i | z
k 1
)
T
p( zk 1 | z k , i )
N
p( z
j 1
k 1
| z k , j ) p( j | z k )
xk 1 f k ( xk , ) g k ( xk , )wk , k 0,1,2,...,
p( i | z k ) ,
z k hk ( x k , ) q k ( )v k , k 0,1,2,.. .
x̂k 1|k ( i ) f k x̂k ( i ), i ,
1
Kk 1( i ) Pk 1|k ( i )H k 1( i )T H k 1( i )Pk 1|k ( i )H k 1( i )T qk 1( i )Rk 1qk 1( i )T E ,
f x̂ ( ),
f x̂ ( ),
T
Pk 1|k ( i ) k k i i Pk ( i ) k k i i g k x̂k ( i ), i Qk g k x̂k ( i ), i ,
x̂k
x̂k
T
Pk 1( i ) Pk 1|k ( i ) Kk 1( i )T H k 1( i )Pk 1|k ( i ) .
13.
Слайд 12РЕГУЛЯРИЗОВАННЫЕ АЛГОРИТМЫ ОЦЕНИВАНИЯ
НА ОСНОВЕ ФОРМАЛЬНОЙ МОДЕЛИ ДВИЖЕНИЯ
УПРАВЛЯЕМОГО ОБЪЕКТА
S 1
l
l
l
y( t ) d s s ( t ) z lp y (pl ) vlp , l 0, L 1, p 0, P 1, y p ( t ) d y( t ) dt
s 0
J z y
2
t t p
.
z d z d ,
T
T
T
z z0 , z1 ,..., zL 1 , z j z j 0 , z j1 ,..., z j ,P 1 , j 0, L 1 , 0 , 1 ,..., L 1 ,
j { (psj ) , p 0, P 1, s 0, S 1}T , j 0, L 1 ,
T
y y0 , y1 ,..., yL 1 , y y0( j ) , y1( j ) ,..., y P( j 1) , j 0, L 1 , d { d 0 , d1 ,..., d S 1 }T .
T
d z ,
h, z z ,
hd1 z hd1 d1 z z h d1
14.
Слайд 12РЕГУЛЯРИЗОВАННЫЕ АЛГОРИТМЫ ОЦЕНИВАНИЯ
НА ОСНОВЕ ФОРМАЛЬНОЙ МОДЕЛИ ДВИЖЕНИЯ
УПРАВЛЯЕМОГО ОБЪЕКТА
d B h z , d B h z ,
B h g ( Th h ) Th ( Th h I ) 1 Th , B h B h h B h .
d n ,a ( Th h I ) 1( d n 1, Th z ), n 1,..., m ,
d n ,a ( Th h I ) 1( d n 1, Th h d m , ), n 1,...,m ., d r d m , , d r d m , ( r 1 ),
j
1
1
1
gr ( )
1
,
r
,
j 1
m
( 1 r )
j 0 ( )
m 1
Brh B
(m)
h
m 1
j ( Th h I ) ( j 1 ) Th , Brh B ( hm ) B ( hm ) h B ( hm ) ,
j 2
h dr z b( dr h ), b 1 .
15.
Слайд 13СХЕМА УСТАНОВКИ ДЛЯ ВЫПАРИВАНИЯ
ПУЛЬПЫ АММОФОСА
1 – напорный бачок; 2 – аммонизаторы; 3 – топка; 4 – брызгоуловитель; 5 – барботажная труба; 6 – регулятор
уровня; 7 – выпарной аппарат; 8 – хранилище исходной кислоты; 9 – центробежные насосы; 10 – сборники;
11 – сборник циркуляционного раствора; 12 – полый скруббер
16.
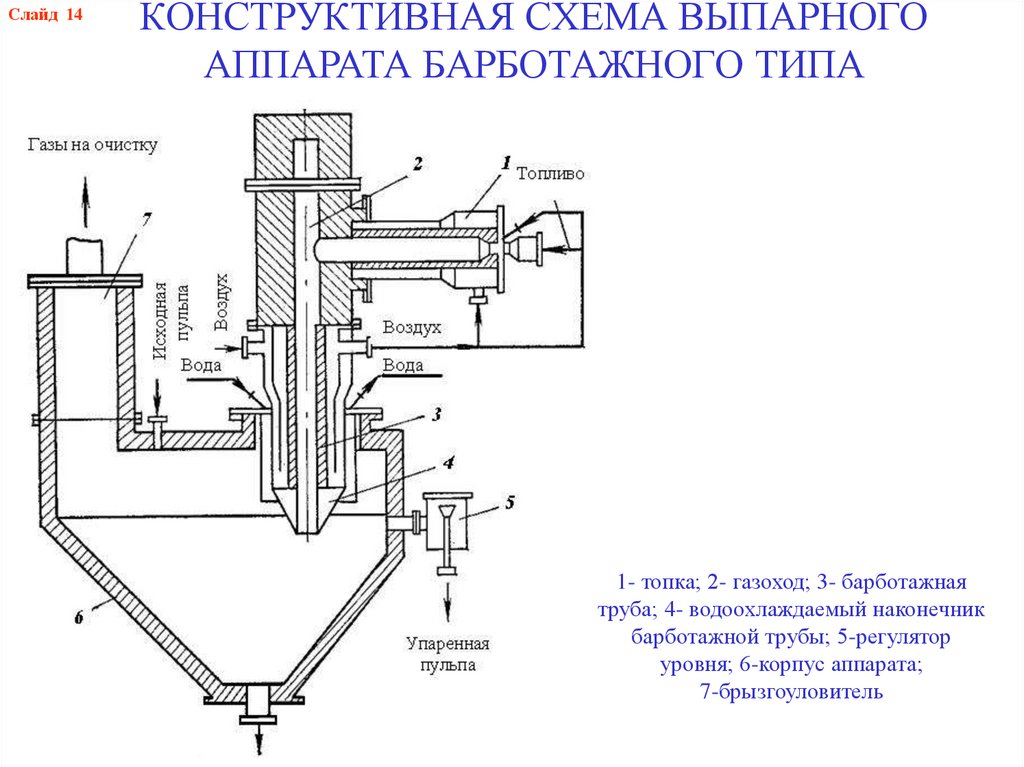
Слайд 14КОНСТРУКТИВНАЯ СХЕМА ВЫПАРНОГО
АППАРАТА БАРБОТАЖНОГО ТИПА
1- топка; 2- газоход; 3- барботажная
труба; 4- водоохлаждаемый наконечник
барботажной трубы; 5-регулятор
уровня; 6-корпус аппарата;
7-брызгоуловитель
17.
Слайд 15ПОКАЗАТЕЛИ РАБОТЫ ПРОМЫШЛЕННОГО ВЫПАРНОГО
АППАРАТА БАРБОТАЖНОГО ТИПА
Производительность, т/ч
по исходной пульпе
по выпаренной воде
32-36
8-10
Влажность пульпы, %
исходной
упаренной
60-65
35-40
Расход природного газа (Q=34.8 МДж/ м3), м3 /ч
Удельный расход на выпаривание 1 т воды
природного газа, м3/т
электроэнергии, кВт ч
700-800
90
16-20
Влагосъем, кг/ч
с 1 м3 рабочего объема аппарата
с 1 м2 зеркала испарения
600-700
330-400
Температура, оС
топочных газов в барботажной трубе
отходящих газов из аппарата
исходной пульпы
упаренной пульпы
600-800
90-95
85-90
80-90
Глубина погружения барботажной трубы, мм
Скорость газа в барботажной трубе, м/с
Давление, кПа, в барботажной трубе
в аппарате
Содержание в отходящих газах, мг/ м3
аммиака
фтора
250
60-80
440-540
98.1
50-70
10-15
18.
Слайд 16ФОРМАЛИЗАЦИЯ ПРОЦЕССА ВЫПАРКИ АММОФОСНОЙ
ПУЛЬПЫ КАК ОБЪЕКТА УПРАВЛЕНИЯ
Управляющие параметры U=(u1,u2,), где u1 – расход пульпы на упарку;
u2 – расход природного газа;
Выходные параметры Y = (y1,y2), где y1 – плотность упаренной пульпы;
y2
– температура упаренной пульпы;
Возмущающие воздействия W = (w1,w2), где w1 –плотность пульпы на входе в
аппарат; w2 – влажность0 исходной
пульпы.
0
xk 1 Ak xk Bk uk wk , xk x0 , y k C k xk vk , k {k 0 , k1 ,..., kT } ,
0
a110 ,k
A 0
a 21,k
0
k
a120 ,k
,
0
a 22
,k
b110 ,k
B 0
b21,k
b120 ,k
1 0
Ck
,
0 ,
b22
0
0
,k
0
k
M [ x 0 ] 0, M [ x 0 x 0T ] X 0 , M [v k ] 0, M [ x 0 v kT ] 0, M [ x 0 wkT ] 0,
w
W
M k wlT v lT T
v k
G
G
k l .
V
T a T bT , k 1 k w k , aT (a11, a12 , a21, a22 ) , bT (b11, b12 , b21, b22 )
xk 1 Ak0 xk Bk0uk wk , xk0 x0 ,
k 1 k w k ,
y k Ck xk vk ,
M[w k , w Tl ] Qkx kl , M[w k , w l T ] Qk kl , Qkx Rk ,
19.
Слайд 17x p T [ xT | T ] ,
xkp 1 f p [ xkp ,u k ,k ] w kp ,
z k 1 h[ xkp ,u k ,k ] w k ,
xk p f [ xk , k , uk , k ]
wk
p
x , f
,
w
,
k
k
k
wk
x1,k 1 x3,k x1,k x4,k x2,k x7,k u1,k x8,k u2,k w1,k
p
k
x2,k 1 x5,k x1,k x6,k x2,k x9,k u1,k x10,k u2,k w2,k ,
x3,k 1 a11,k 1 a11,k wa1 1,k ,
x4,k 1 a12,k 1 a12,k wa1 2 ,k ,
x5,k 1 a21,k 1 a21,k wa2 1,k ,
x6,k 1 a22,k 1 a22,k wa2 2 ,k ,
x7 ,k 1 b11,k 1 b11,k wb1 1,k ,
x8,k 1 b12,k 1 b12,k wb1 2 ,k ,
x9,k 1 b21,k 1 b21,k wb2 1,k ,
x10,k 1 b22,k 1 b22,k wb2 2 ,k ,
y1,k x1,k w1,k ,
y2,k w2,k .
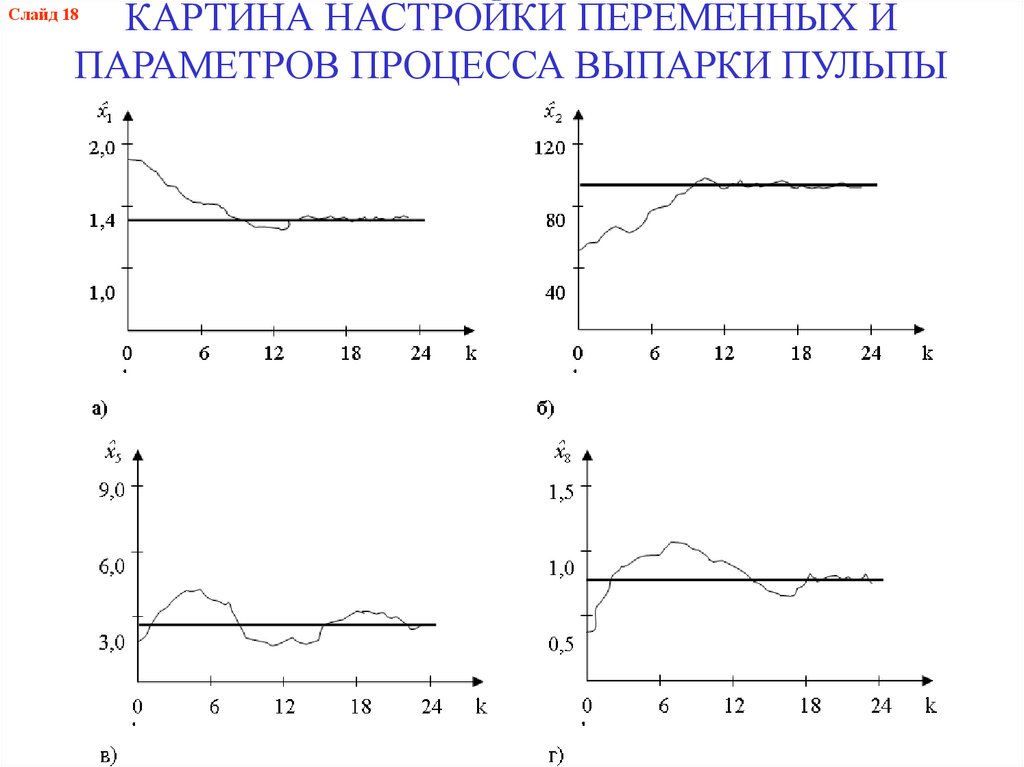
20.
КАРТИНА НАСТРОЙКИ ПЕРЕМЕННЫХ ИПАРАМЕТРОВ ПРОЦЕССА ВЫПАРКИ ПУЛЬПЫ
Слайд 18
21.
АЛГОРИТМЫ СИНТЕЗА СИСТЕМЫ АДАПТИВНОГОСУБОПТИМАЛЬНОГО УПРАВЛЕНИЯ ПРОЦЕССОМ ВЫПАРКИ
АММОФОСНОЙ ПУЛЬПЫ
Слайд 19
kT 1
0 xk
1 T
T T Q
,
J ( x ,u ) M xkT FxkT xk u k
2
k k0
0 R u k
x p T [ xT | T ] ,
u k R 1 Bk T S k x̂k ,
x̂k 1 Ak x̂k Bk uk K k [ zk Cx̂k ] ,
x̂0 0 ,
trM zk Cx̂k zkT0 0, k0 k1 k ,
kT
Cx̂
kT
k 1 k tr M ( z Cx̂ )k zk1 M zk1 , k0 0 ,
k
kT
Cx̂
k
k 1 k tr M ( z Cx̂ )k zk1 M zk1 , k0 0 ,
k
kT
Cx̂
k
k 1 k tr M ( z Cx̂ )k zk1 M zk1 , k0 0 ,
k
22.
Слайд 19x̂k 1 Ak x̂k Bk uk K k [ zk Cx̂k ] ,
x̂0 0 ,
Ô x̂ u 0 , Ô A0 A , B 0 B ,
x̂k 1 A0 x̂k B 0uk wk Ô x̂k uk A xk B uk wk Ô k ,
~
xk 1 Ak ~
xk Bk u~k , ~
x k0 0 ,
~
kT 1
xk
Q
0
1
T
T ~T
~
~
~
~
~
~ ,
J ( x ,u ) x ( N )Fx ( N ) xk uk
2
k k0
0 R uk
u~k R 1 Bkô T S kô ~
xk ,
S
S kô0 S0ô ,
ô
k 1
~
~ ,S ô )
H
(
x
,
u
k
k
k
H ( ~
xk ,u~k , S )
,
ô
S k
ô
k
H( ~
xk ,u~k , S kô ) 0,5~
xkT Q ~
xk 0,5 u~kT R u~k ~
xkT S kô ~
xk ,
kT 1
J ( x̂ ,u ) J ( ~
x ,u~ ) 0,5tr S kô K kô VK kô T .
k k0
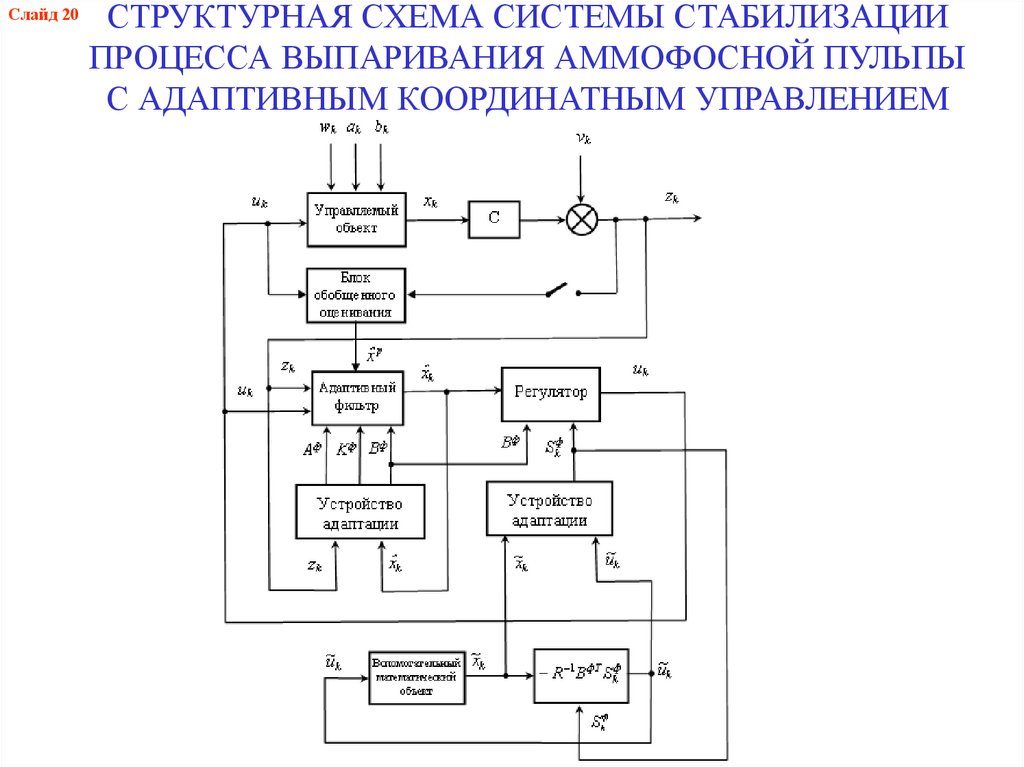
23.
Слайд 20СТРУКТУРНАЯ СХЕМА СИСТЕМЫ СТАБИЛИЗАЦИИ
ПРОЦЕССА ВЫПАРИВАНИЯ АММОФОСНОЙ ПУЛЬПЫ
С АДАПТИВНЫМ КООРДИНАТНЫМ УПРАВЛЕНИЕМ
24.
Таким образом, в работе на основеконцепций
системного
анализа,
идентификации, динамической фильтрации и
методов
решения
некорректных
задач
разработаны
регуляризованные
единые
алгоритмы координатного и параметрического
оценивания
технологических
объектов
управления
в
условиях
априорной
неопределенности, позволяющие существенно
повысить эффективность функцинирования
систем
управления
технологическими
объектами.
















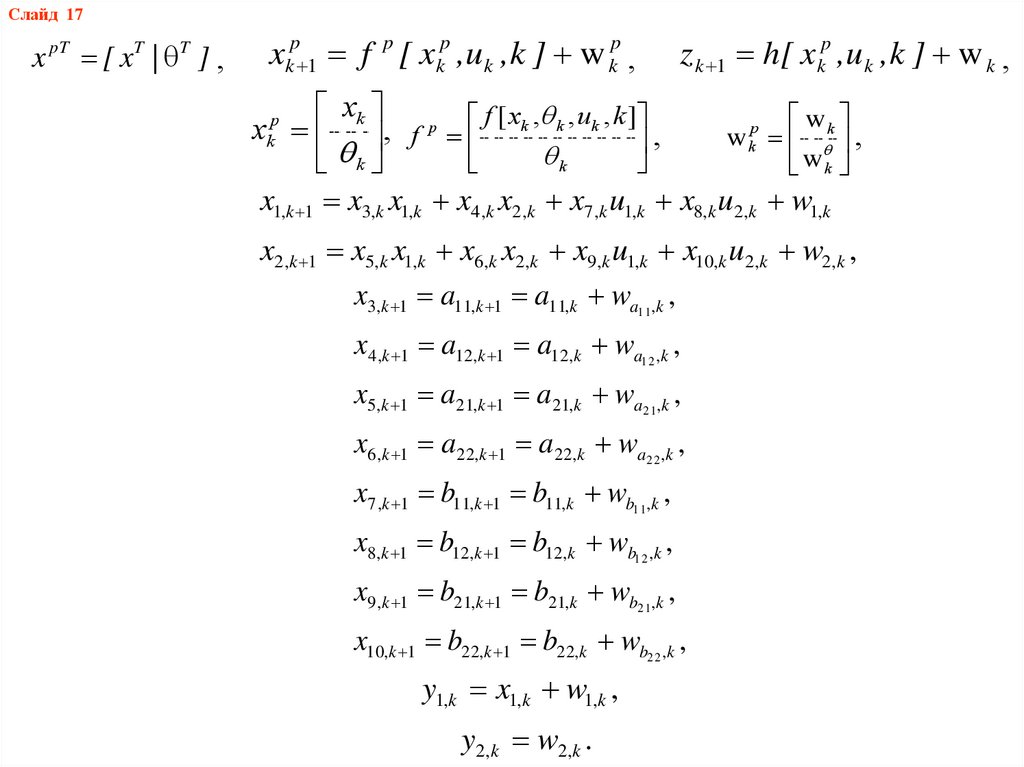

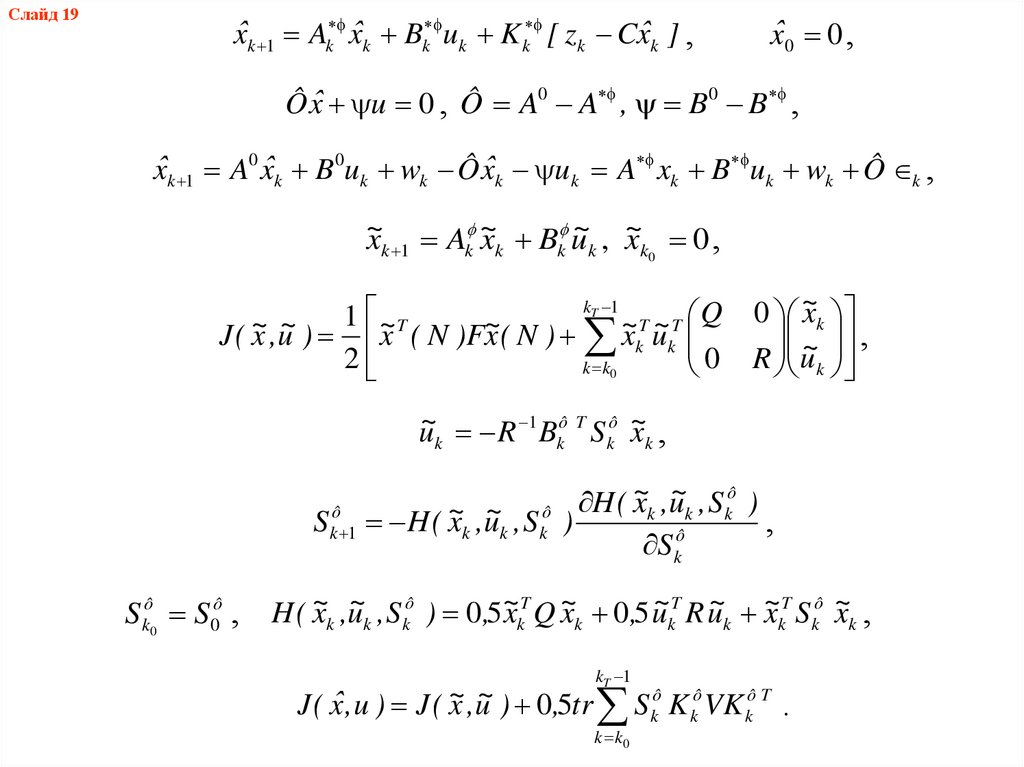

 Электроника
Электроника