Трехфазная система передачи электрической энергии

1.

ЭЛЕКТРОТЕХНИКА
4. ТРЕХФАЗНАЯ СИСТЕМА
ПЕРЕДАЧИ ЭЛЕКТРИЧЕСКОЙ
ЭНЕРГИИ

2.

Лекция 1 (продолжение – 1.36)
ТРЕХФАЗНАЯ СИСТЕМА
ПЕРЕДАЧИ
ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ
40

3.

Лекция 1 (продолжение – 1.36)
3.1. Принцип получения трехфазной симметричной
синусоидальной системы ЭДС
Трехфазная система электрических цепей представляет
собой совокупность электрических цепей, в которых
действуют три синусоидальные ЭДС одной и той же
частоты, сдвинутые друг относительно друга по фазе и
создаваемые общим источником энергии.
Если все три ЭДС равны по значению и сдвинуты по фазе
на 120° по отношению друг к другу, то такая система ЭДС
называется симметричной. Аналогично определяются
трехфазные системы напряжений и токов.
40

4.

Лекция 1 (продолжение – 1.37)
Рис. 1. Трехфазная система ЭДС:
а – симметричная; б, в – несимметричная
41

5.

Лекция 1 (продолжение – 1.37)
Часть трехфазной системы электрических цепей, в
которой может протекать один из токов трехфазной
системы, называется фазой.
Т.о., фазой являются обмотка генератора, в которой
индуцируется ЭДС, и приемник, присоединенный к
этой обмотке.
Преимущества трехфазной системы экономичная и на большие расстояния
передача электрической энергии и
превосходное качество двигателей.
41

6.

Лекция 1 (продолжение – 1.38)
Трехфазная система ЭДС создается трехфазными
генераторами. В неподвижной части генератора
(статоре) размещают три обмотки сдвинутые в
пространстве на 120°.
На вращающейся части генератора (роторе)
располагают обмотку возбуждения, которая
питается от источника постоянного тока.
Ток обмотки возбуждения создает магнитный поток
Ф0, постоянный (неподвижный) относительно
ротора, но вращающийся вместе с ним с частотой п.
Вращение ротора осуществляется каким-либо
двигателем.
42

7.

Лекция 1 (продолжение – 1.38)
42

8.

Лекция 1 (продолжение – 1.38)
Благодаря конструктивным приемам магнитный поток
Ф0 в воздушном зазоре между статором и ротором
распределяется по синусоидальному закону по
окружности.
Поэтому при вращении ротора вращающийся вместе с
ним магнитный поток пересекает проводники обмоток
статора и индуцирует в них синусоидальные ЭДС.
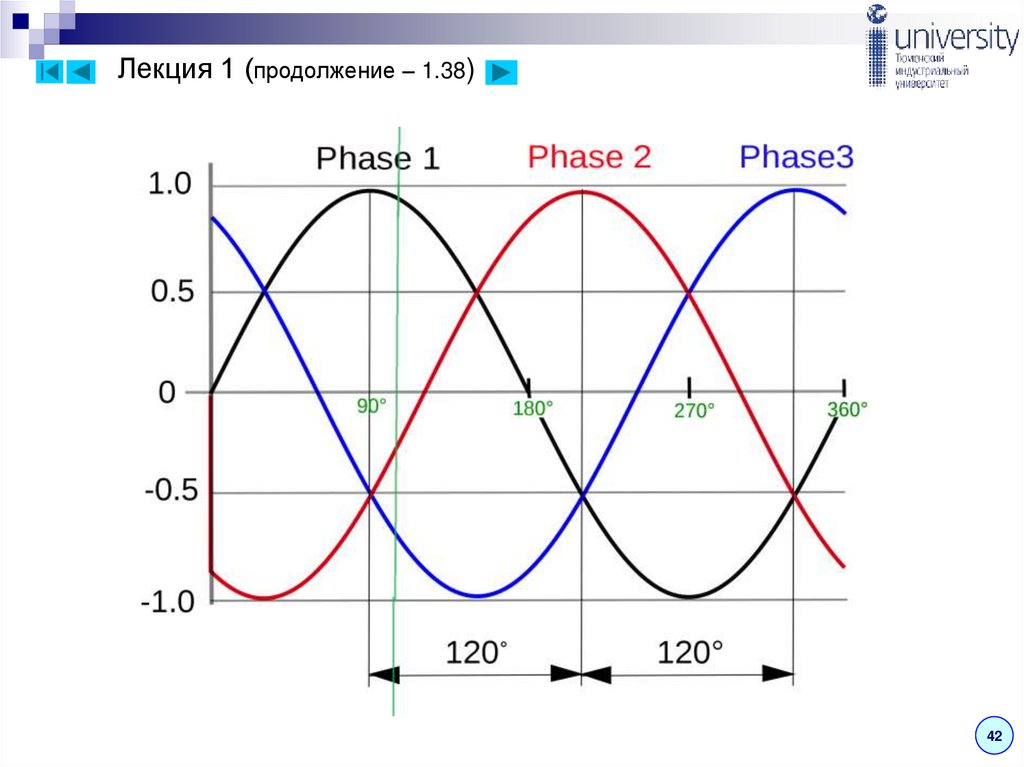
Т. о., ЭДС в каждой последующей фазе будет отставать
от ЭДС в предыдущей фазе на 1/3 периода, т. е. на угол
2π/3.
Если принять, что для фазы А начальная фаза равна
нулю, то ЭДС фазы,
а ЭДС фазы В
и ЭДС фазы С
42

9.

Лекция 1 (продолжение – 1.38)
42

10.

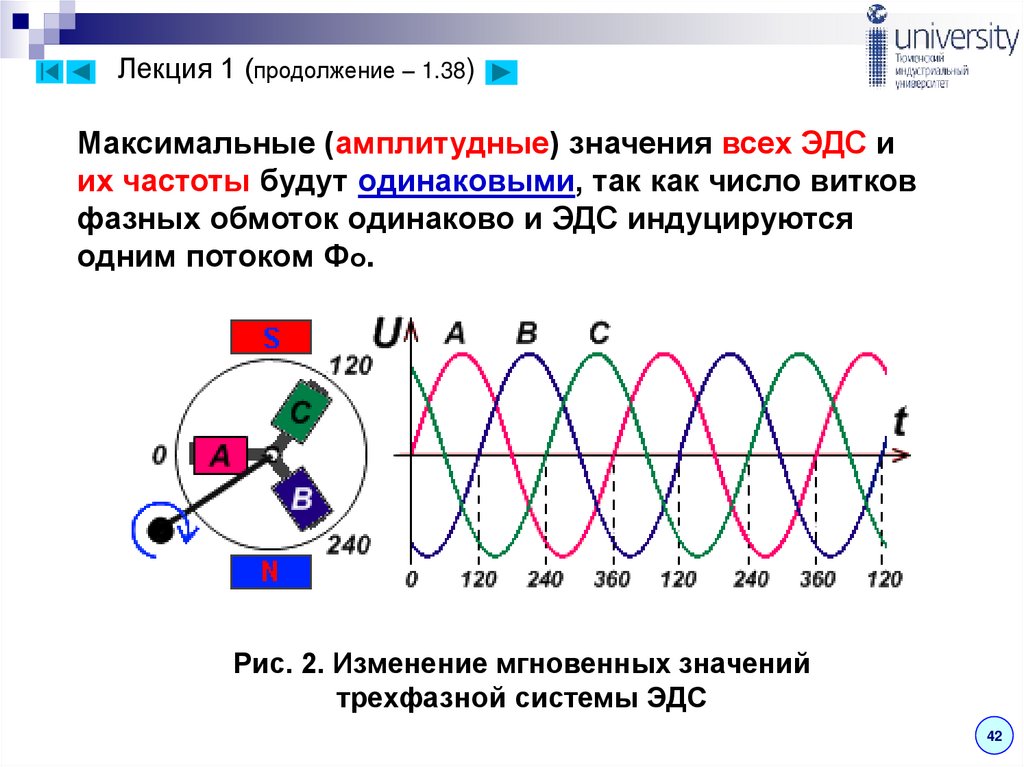
Лекция 1 (продолжение – 1.38)
Максимальные (амплитудные) значения всех ЭДС и
их частоты будут одинаковыми, так как число витков
фазных обмоток одинаково и ЭДС индуцируются
одним потоком Фо.
Рис. 2. Изменение мгновенных значений
трехфазной системы ЭДС
42

11.

Лекция 1 (продолжение – 1.39)
3.2. Схемы соединения элементов трехфазных
устройств. Понятия о линейных и фазных токах
и напряжениях
Если все нагрузочные сопротивления равны
по значению и имеют одинаковый характер,
нагрузка называется симметричной, в
противном случае нагрузка называется
несимметричной.
Возможны различные схемы соединения
обмоток генератора или фаз приемника –
звездой или треугольником.
43

12.

Лекция 1 (продолжение – 1.40)
3.2.1. Соединение обмоток генератора и фаз
приемника звездой
Каждая фаза трехфазного генератора может
являться источником питания для однофазного
приемника.
В этом случае схема электрической цепи имеет
вид, изображенный на рис. 3, т. е. каждая фаза
работает отдельно от других, хотя в целом цепь
является трехфазной.
Это трехфазная несвязанная система (на практике
она никогда не применяется, но для рассмотрения
вопроса очень удобна).
44

13.

Лекция 1 (продолжение – 1.40)
Рис. 3. Схема трехфазной несвязанной
электрической цепи
44

14.

Лекция 1 (продолжение – 1.40)
Принимая равными потенциалы точек,
соответствующих концам X, У и Z обмоток
фаз генератора, можно объединить их в одну точку N
(рис. 4.).
Концы фаз приемников (Zа, Zb и Zс) также соединяем
в одну точку n. Такое соединение обмоток генератора
называется соединением звездой.
Звездой можно соединять также фазы приемника.
Точки N и n называются нейтральными, а провод,
соединяющий точку N генератора с точкой n
приемника, – нейтральным.
Провода А—а, В—b и С—с, соединяющие начала фаз
генератора и приемника, называются линейными.
44

15.

Лекция 1 (продолжение – 1.40)
Рис. 4. Схема связанной
четырехпроводной трехфазной цепи.
44

16.

Лекция 1 (продолжение – 1.40)
Напряжение между началом и концом фазы – фазное
напряжение Uф .
Т. o., имеется три фазных напряжения – UА, UВ, UС.
Обычно за условное положительное направление ЭДС
генератора принимают направление от конца к началу
фазы.
Положительное направление тока в фазах совпадает с
положительным направлением ЭДС, а положительное
направление падения напряжения (напряжение) на
фазе приемника совпадает с положительным
направлением тока в фазе.
Положительным направлением напряжения на фазе
генератора, как и на фазе приемника, является
направление от начала фазы к ее концу, т. е.
противоположное положительному направлению ЭДС.
44

17.

Лекция 1 (продолжение – 1.41)
Напряжение между линейными проводами – линейное
напряжение UЛ. Имеется три линейных напряжения –
UАВ, UВС, UСА, условные положительные направления
которых приняты от точек, соответствующих первому
индексу, к точкам, соответствующим второму индексу.
Линейные напряжения определяются через известные
фазные напряжения.
Это соотношение может быть получено из уравнения,
написанного по второму закону Кирхгофа для контура
АNВА, если принять направление обхода контура от
точки А к точке N и т. д.
Отсюда
Т.о., действующее значение линейных
напряжений равно векторной разности
соответствующих фазных напряжений.
45

18.

Лекция 1 (продолжение – 1.40)
Рис. 4. Схема связанной
четырехпроводной трехфазной цепи.
Рис. 5. Векторная диаграмма фазных
и линейных напряжений при
соединении фаз звездой
44

19.

Лекция 1 (продолжение – 1.40)
На векторной диаграмме напряжений векторы фазных
напряжений образуют звезду, а векторы линейных
напряжений – замкнутый треугольник.
Вследствие этого векторная сумма линейных
напряжений всегда равна нулю, т. е. UАВ + UВС + UСА = 0
Так как при симметричной системе треугольник
линейных напряжений равносторонний, то, чтобы
найти соотношение между линейными и фазными
напряжениями, надо опустить перпендикуляр из точки
N на вектор напряжения UАВ.
Тогда АВ =UАВ = 2 UВ cos 30°.
Так как
,а
, то
.
Т.о., если система напряжений симметрична, то при
соединении звездой линейное напряжение в
раза больше фазного напряжения.
44

20.

Лекция 1 (продолжение – 1.42)
Предусмотренные ГОСТом и применяемые на
практике напряжения переменного тока 127, 220,
380 и 660В как раз и отличаются друг от друга в
1,73 раза.
Если UЛ = 220 В, то UФ = 127 В, что обозначают
как 220/127 В. Кроме того, применяют системы
380/220 и 660/380 В.
В четырехпроводной трехфазной цепи имеется
два уровня напряжения, различающихся в 1,73
раза, что позволяет использовать приемники с
различным номинальным напряжением.
46

21.

Лекция 1 (продолжение – 1.43)
При подключении приемников к трехфазному
генератору, обмотки которого соединены звездой,
ток протекает по обмоткам генератора, линейным
проводам и фазам приемника.
Ток в фазах генератора или приемника называется
фазным током Iф.
Ток в линейных проводах называется линейным
током IЛ.
Так как обмотка генератора, линейный провод и
приемник, принадлежащие одной фазе, соединяются
последовательно, то при соединении звездой
линейный ток равен фазному: IЛ = I ф.
47

22.

Лекция 1 (продолжение – 1.40)
Рис. 4. Схема связанной
четырехпроводной трехфазной цепи.
Рис. 5. Векторная диаграмма фазных
и линейных напряжений при
соединении фаз звездой
44

23.

Лекция 1 (продолжение – 1.43)
Ток в нейтральном проводе IN может быть
определен по первому закону Кирхгофа, на
основании которого для точки n можно
записать уравнение IA + IB + IC - IN = 0.
Откуда
IN = IA + IB + IC.
Следовательно, ток в нейтральном проводе
равен геометрической сумме фазных токов.
47

24.

Лекция 1 (продолжение – 1.44)
48

25.

Лекция 1 (продолжение – 1.46)
50

26.

Лекция 1 (продолжение – 1.46)
50

27.

Лекция 2 (продолжение – 3.73)
73

28.

Лекция 2 (продолжение – 3.73)
73

29.

Лекция 2 (продолжение – 3.73)
73

30.

Лекция 2 (продолжение – 3.73)
73

31.

Лекция 2 (продолжение – 3.73)
Рассмотрим порядок построения расчетных формул на
примере сопротивлений и ЭДС.
1) Заданы Z ( Ом ) ,
Z *б
Z (Ом )
Z б (Ом )
E( кВ ) .
(k1k2 k3 ...kn )
2
Z (Ом ) 3 I б
Uб
(k1k2 k3 ...k n ) 2
(4.17)
Sб
Sб
2
Z (Ом ) 2 (k1k2 k3 ...kn ) Z ( Ом )
.
Uб
U б2
1
Здесь: U б U б
− базисное напряжение,
(k1k2 k3 ...kn )
приведенное на расчетную ступень.
E *б
E( кВ )
U б ( кВ )
(k1k2 k3 ...kn )
E( кВ )
(4.18)
U б ( кВ )
Формулы (4.17) и (4.18) являются формулами
точного приведения.
73

32.

Лекция 2 (продолжение – 3.73)
При приближенном приведении
Z *б
Z (Ом ) U осн 2 Z (Ом ) 3 I б U осн 2
Sб U осн 2
(
)
(
) Z (Ом ) 2 (
)
Z б (Ом ) U ну
Uб
U ну
U б U ну
E( кВ ) U осн
E *б
(
)
U б ( кВ ) U ну
(4.19)
(4.20)
где U ну − номинальное напряжение ступени, где
установлен элемент.
При обычно используемом условии U б U осн формулы
принимают вид:
Z *б
Sб
Z (Ом ) 2
U ну
E *б
E( кВ )
U ну ( кВ )
E *н
(4.21)
73

33.

Лекция 2 (продолжение – 3.73)
2) Заданы
Z *б
Z (Ом )
Z н , E н .
Z н Z н
(k1k2 k3 ...kn )
(k1k2 k3 ...kn ) 2
Z б (Ом )
Z б (Ом )
2
(4.22)
Z нU нп 3 I б
SбU нп2
SбU нп2
2
2
(k1k2 k3 ...kn ) Z н
(k1k2 k3 ...kn ) Z н
;
2
2
SнU б
Uб 3 Iн
Sн U б
E( кВ )
E нU нп ( кВ )
E нU нп ( кВ )
E *б
(k1k2 k3 ...kn )
(k1k2 k3 ...kn )
(4.23)
U б ( кВ )
U б ( кВ )
U б ( кВ )
Здесь U нп − номинальное паспортное напряжение
элемента.
Формулы (4.22) и (4.23) являются формулами
точного приведения.
73

34.

Лекция 2 (продолжение – 3.73)
При приближенном приведении
Z *б
Z (Ом ) U осн 2 Z н Z н U осн 2 Z нU нп 3 I б U осн 2
(
)
(
)
(
)
Z б (Ом ) U ну
Z б ( Ом ) U ну
U ну
Uб 3 Iн
SбU нп2 U осн 2
SбU нп2
(4.24)
Z н
(
) Z н
;
2
2
S нU б U ну
Sн U б
E( кВ ) U осн
E нU нп ( кВ ) U осн
E нпU нп ( кВ )
E *б
(
)
(
)
.
(4.25)
U б ( кВ ) U ну
U б ( кВ ) U ну
U б ( кВ )
При обычно используемых условиях
U нп = U ну формулы принимают вид:
Z *б Z
н
Sб
; E *б E н
Sн
U б U осн и
(4.26)
В дальнейшем индекс приведения будет опускаться.
73

35.

Лекция 2 (продолжение – 3.73)
4.4. Определение сопротивления элементов
электрических систем и их схемы замещения
Формулы определения сопротивлений приведены
в относительных единицах при приближенном
приведении к базисным условиям.
Генераторы. У генераторов практически никогда
не учитывается активное сопротивление, так как
оно пренебрежительно мало по сравнению с
индуктивным.
73

36.

Лекция 2 (продолжение – 3.73)
Номинальное сопротивление генератора в
относительных единицах х*н может быть
определено из паспортных данных:
− хd , хq − синхронные сопротивления по
продольной и поперечной оси, которые
характеризуют установившийся режим.
− хd и хq , хd и хq − переходные и сверхпереходные
сопротивления в момент времени t = 0.
− х2 , х0 − сопротивления обратной и нулевой
последовательностей.
Номинальное сопротивление генератора в
относительных единицах при базисных условиях
определяется формулой:
Sб
.
xг х н
Sн
73

37.

Лекция 2 (продолжение – 3.73)
Двигатели. Параметры синхронных электродвигателей
определяются аналогично генераторам.
Реакторы. Токоограничивающие реакторы могут
иметь различное устройство и конструктивное
исполнение, а также технические и техникоэкономические характеристики и параметры.
Линейные реакторы, включаемые последовательно
в соответствующую линию, ограничивают ток КЗ и
поддерживают относительно высокий уровень
остаточного напряжения. Сопротивление линейного
реактора можно определить по формуле:
где
х р (Ом)
Sб
xР х р (Ом)
2
U нр
,
лежит в пределах 0,1…0,4 Ом.
73

38.

Лекция 2 (продолжение – 3.73)
Сдвоенный реактор обладает лучшими
характеристиками. Между ветвями реактора
существует магнитная связь, которая в сквозном
режиме позволяет уменьшить потери напряжения в
реакторе. Коэффициент магнитной связи идентичных
ветвей обмотки реактора равен:
М
M
Kсв
0,4...0,6 .
L
L1L2
Сдвоенный реактор имеет 3 режима работы:
Одноцепный режим
Двухцепный (сквозной) режим
Продольный режим
73

39.

Лекция 2 (продолжение – 3.73)
Трансформаторы
Двухобмоточный трансформатор. Схема замещения
двухобмоточного трансформатора приведена на
рисунке 4.13.
Рис. 4.13. Условное обозначение и схема замещения
двухобмоточного трансформатора
73

40.

Лекция 2 (продолжение – 3.73)
Параметры схемы замещения производятся по
данным:
опыта ХХ;
опыта КЗ.
Опыт ХХ (рис. 4.14) позволяет определить
ток ХХ I xx , потери в ветви намагничивания Pxx
и сопротивление ХХ.
Потери ХХ:
Pxx I xx2 (r1 r ) I xx2 r
Сопротивление ХХ:
Рис. 4.14. Опыт ХХ
Р Sб
Uн
z1 z
z r*
Sn Sн
3I xx
73

41.

Лекция 2 (продолжение – 3.73)
Опыт КЗ (рис. 4.15) позволяет определить напряжение
КЗ и потери КЗ:
uк ,% Sб
, следовательно,
zТ
100 Sн
индуктивное сопротивление
рассеивания определяется как
хТ zТ 2 rТ 2
Рис. 4.15. Опыт КЗ
Напряжение короткого замыкания
u (4...13) % .
к
2
Потери короткого замыкания: Pк 3I н rф .
Рк
Активное сопротивление трансформатора: rф (Ом)
2 .
3I н
Пренебрегая ветвью намагничивания
схему замещения (рис. 4.16):
z , получим упрощенную
Рис. 4.16. Схема замещения
хТ х1 х2
73

42.

Лекция 2 (продолжение – 3.73)
Активное сопротивление трансформатора в относительных
единицах, приведенное к базисным условиям:
Sб U б2 Рк Sб Рк ( 3U н )2 Sб Рк Sб
Sб ,
rТ б
rф 2 2 2 2
r н
2
2
2
rб U н
U б U н 3I н U н
3Sн
Uн
Sн Sн
Sн
Рк ,%
где r н
− номинальное активное сопротивление в
100
относительных единицах.
rф U б2
73

43.

Лекция 2 (продолжение – 3.73)
Трехобмоточный трансформатор
Рис. 4.17. Условное обозначение и схема
замещения трехобмоточного трансформатора
73

44.

Лекция 2 (продолжение – 3.73)
В относительных единицах напряжения КЗ обмоток будут
равняться их сопротивлениям рассеивания и их значения для
обмоток высшего, среднего и низшего напряжений
трехобмоточного трансформатора могут быть определены по
формулам:
uК ВН xBH xB xH
uК CН xCH xC xH
uК ВC xBC xB xC
где
U к ,%
uK
100
1
Sб
xB ( xBH xBC xCH )
2
S НВ
1
Sб
xС ( xBС xCН xВH )
2
S НС
1
Sб
xН ( xBH xСН xВC )
.
2
S НН
Данные формулы справедливы и для автотрансформатора,
обычно в расчеты не вводится.
73

45.

Лекция 2 (продолжение – 3.73)
Трансформатор с расщепленной обмоткой. На
электростанциях и подстанциях применяются силовые
трансформаторы и автотрансформаторы с расщепленной
обмоткой низшего напряжения, так как это позволяет
существенно снизить ток КЗ в сетях низшего напряжения.
Повышающие трансформаторы и автотрансформаторы с
расщепленной обмоткой используются для формирования
укрупненных блоков электростанций, особенно на ГЭС.
Рис. 4.18 Условное обозначение трансформатора с расщепленной обмоткой:
а) обмотка низшего напряжения расщеплена на 2 части;
б) обмотки низшего напряжения расщеплена на 3 части
73

46.

Лекция 2 (продолжение – 3.73)
73

47.

Лекция 2 (продолжение – 3.73)
73