Модели данных. Лекция 2

1. Базы данных

Модели данных

2.

Модель данных – совокупность структур
данных (типов связей между данными) и
операций их обработки.

3.

Иерархическая модель – это упорядоченный набор
веерных отношений (потомок-предок), в котором для каждого
потомка существует единственный предок.
Иерархическая модель позволяет строить БД с древовидной
структурой. В них каждый узел содержит свой тип данных
(сущность). На верхнем уровне дерева имеется один узел –
корень, на следующем уровне располагаются узлы, связанные с
этим корнем, затем узлы, связанные с узлами предыдущего
уровня, и т. д. Каждый узел может иметь только одного предка.
Поиск данных всегда начинается с корня. Затем производится
спуск с одного уровня на другой пока не будет достигнут искомый
уровень. Перемещения от одной записи к другой осуществляются с
помощью ссылок.
Достоинствами иерархической модели являются простота
описания иерархических структур реального мира, а также быстрое
выполнение запросов, соответствующих структуре данных.
Недостатки иерархической модели в том, что они часто
содержат избыточные данные и не всегда удобно каждый раз
начинать поиск нужных данных с корня.

4.

Организация данных в СУБД иерархического типа определяется в
терминах: элемент, агрегат, запись (группа), групповое отношение,
база данных.
•Атрибут (элемент данных) - наименьшая единица структуры
данных. Обычно каждому элементу при описании базы данных
присваивается уникальное имя. По этому имени к нему
обращаются при обработке. Элемент данных также часто называют
полем.
•Запись - именованная совокупность атрибутов. Использование
записей позволяет за одно обращение к базе получить некоторую
логически связанную совокупность данных. Именно записи
изменяются, добавляются и удаляются. Тип записи определяется
составом ее атрибутов.
•Групповое отношение - иерархическое отношение между
записями двух типов. Родительская запись (владелец группового
отношения) называется исходной записью, а дочерние записи
(члены группового отношения) - подчиненными. Иерархическая
база данных может хранить только такие древовидные структуры.

5.

Корневая запись каждого дерева обязательно должна содержать
ключ с уникальным значением. Ключи некорневых записей должны
иметь уникальное значение только в рамках группового отношения.
Каждая запись идентифицируется полным сцепленным ключом, под
которым понимается совокупность ключей всех записей от корневой по
иерархическому пути.
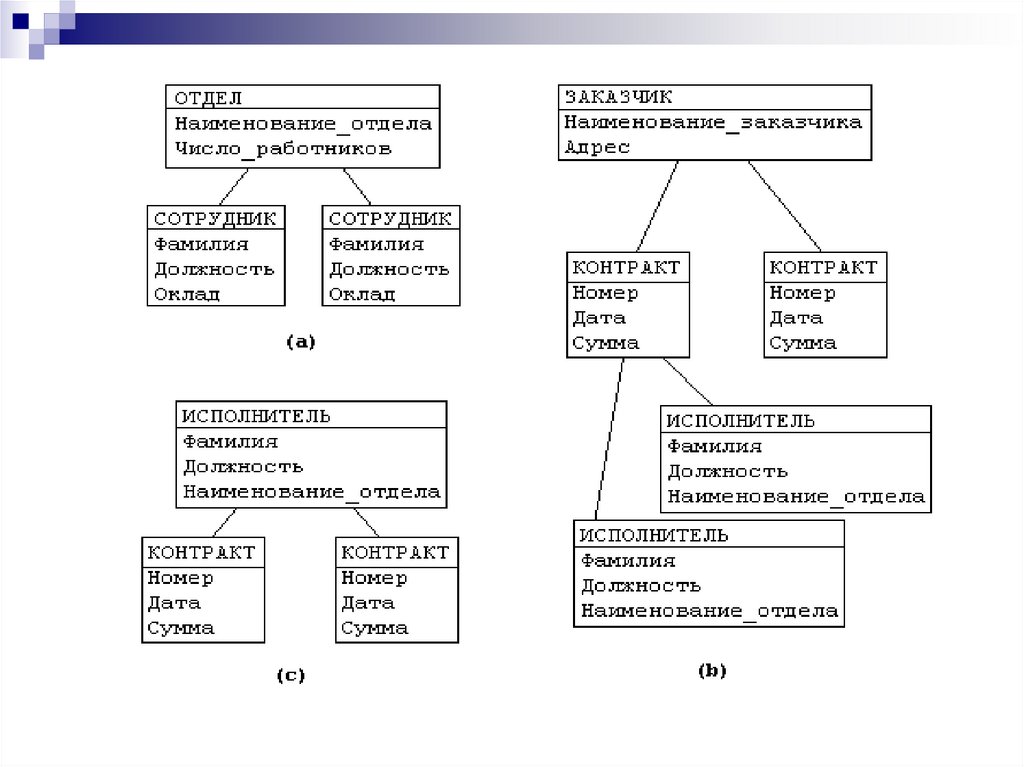
При графическом изображении групповые отношения изображают
дугами ориентированного графа, а типы записей - вершинами
(диаграмма Бахмана).

6.

7.

Операции над данными, определенные в
иерархической модели:
•ДОБАВИТЬ в базу данных новую запись. Для корневой записи
обязательно формирование значения ключа.
•ИЗМЕНИТЬ значение данных предварительно извлеченной записи.
Ключевые данные не должны подвергаться изменениям.
•УДАЛИТЬ некоторую запись и все подчиненные ей записи.
•ИЗВЛЕЧЬ:
•извлечь корневую запись по ключевому значению, допускается
также последовательный просмотр корневых записей .
•извлечь следующую запись (следующая запись извлекается в
порядке левостороннего обхода дерева) .

8.

Ограничения целостности
Поддерживается только целостность связей между
владельцами и членами группового отношения (никакой
потомок не может существовать без предка). Как уже
отмечалось,
не
обеспечивается
автоматическое
поддержание соответствия парных записей, входящих в
разлные иерархии.

9.

Сетевая модель данных
Сетевая модель – это неупорядоченный набор веерных
отношений (потомок-предок).
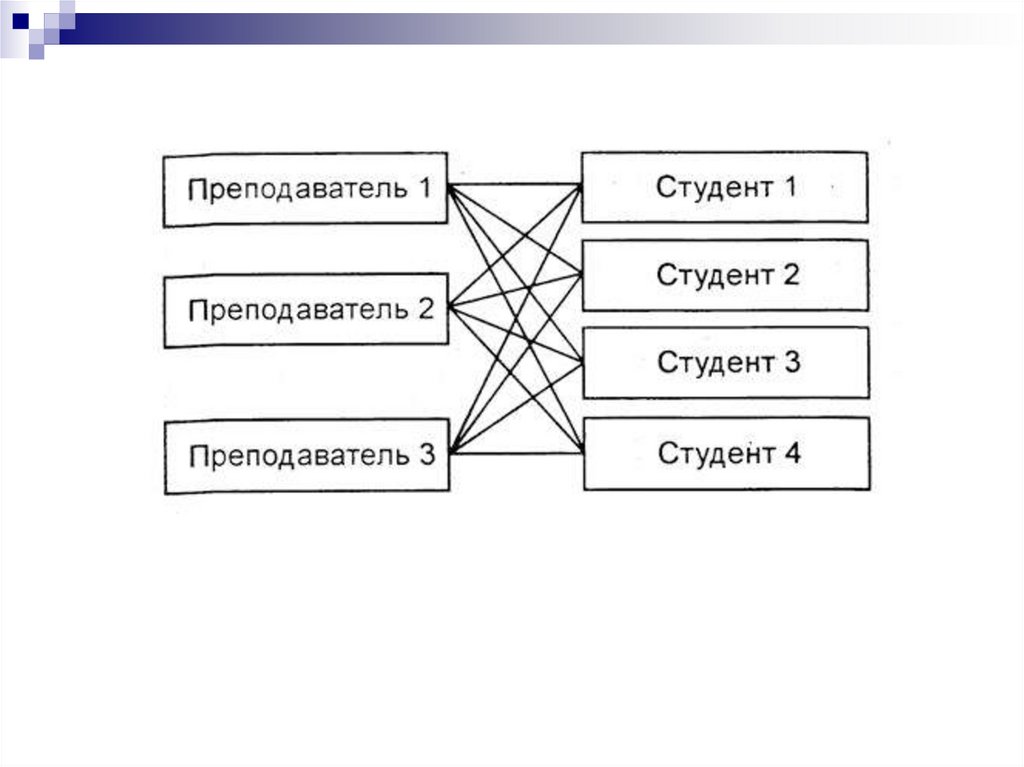
В сетевой модели возможны связи всех информационных
объектов со всеми. Например, каждый преподаватель может
обучать много студентов и каждый студент может обучаться у
многих преподавателей.
На разработку этого стандарта большое влияние оказал
американский ученый Ч.Бахман. Основные принципы сетевой модели
данных были разработны в середине 60-х годов, эталонный вариант
сетевой модели данных описан в отчетах рабочей группы по языкам
баз данных (COnference on DAta SYstem Languages) CODASYL (1971
г.).
Сетевая модель данных определяется в тех же терминах, что и
иерархическая. Она состоит из множества записей, которые могут
быть владельцами или членами групповых отношений. Связь между
между записью-владельцем и записью-членом также имеет вид 1:N.

10.

11.

В сетевой модели каждый экземпляр группового отношения
характеризуется
следующими
признаками
упорядочения
подчиненных записей:
произвольный,
хронологический /очередь/,
обратный хронологический /стек/,
сортированный.
Если запись объявлена подчиненной в нескольких групповых
отношениях, то в каждом из них может быть назначен свой способ
упорядочивания.

12.

Принято выделять три класса членства подчиненных записей
в групповых отношениях:
1. Фиксированное. Подчиненная запись жестко связана с
записью владельцем и ее можно исключить из группового
отношения только удалив. При удалении записи-владельца все
подчиненные записи автоматически тоже удаляются.
2. Обязательное. Допускается переключение подчиненной
записи на другого владельца, но невозможно ее существование
без владельца. Для удаления записи-владельца необходимо,
чтобы она не имела подчиненных записей с обязательным
членством.
3. Необязательное. Можно исключить запись из группового
отношения, но сохранить ее в базе данных не прикрепляя к
другому владельцу. При удалении записи-владельца ее
подчиненные записи - необязательные члены сохраняются в
базе, не участвуя более в групповом отношении такого типа.

13.

Операции над данными
• ДОБАВИТЬ - внести запись в БД и, в зависимости от режима
включения, либо включить ее в групповое отношение, где она
объявлена подчиненной.
• ВКЛЮЧИТЬ В ГРУППОВОЕ ОТНОШЕНИЕ - связать
существующую подчиненную запись с записью-владельцем.
• ПЕРЕКЛЮЧИТЬ - связать существующую подчиненную
запись с другой записью-владельцем в том же групповом
отношении.
• ОБНОВИТЬ - изменить значение элементов предварительно
извлеченной записи.
•ИЗВЛЕЧЬ - извлечь записи последовательно по значению
ключа, а также используя групповые отношения.
•УДАЛИТЬ - убрать из БД запись.
• ИСКЛЮЧИТЬ ИЗ ГРУППОВОГО ОТНОШЕНИЯ - разорвать
связь между записью-владельцем и записью-членом.

14.

Ограничения целостности
Как
и
в
иерархической
модели,
обеспечивается
только
поддержание
целостности по ссылкам (владелец отношения член отношения).

15.

Реляционная модель данных
Реляционная модель предложена сотрудником компании IBM
Е.Ф.Коддом в 1970 г.
В настоящее время эта модель является фактическим
стандартом, на который ориентируются практически все
современные коммерческие СУБД.
В статье Е.Ф.Кодда утверждается, что "реляционная модель
предоставляет средства описания данных на основе только их
естественной структуры, т.е. без потребности введения какойлибо дополнительной структуры для целей машинного
представления".
Другими словами, представление данных не зависит от
способа их физической организации. Это обеспечивается за
счет использования математической теории отношений (само
название "реляционная" происходит от английского relation "отношение").

16. Основные определения

Домен – множество возможных значений некоторой
величины из предметной области.
Примеры доменов
Фамилии = {Иванов, Петров, Сидоров}
Дисциплины = {БД, СПО, ПЯВУ}
D1 = {2,4} D2 = {1,3,5}
Декартово произведение множеств – множество
всевозможных пар элементов из D1 и D2
D1 D2 = {(2,1), (2,3) , (2,5) , (4,1) , (4,3) , (4,5)}

17. Основные определения

Отношение – любое подмножество из декартова
произведения доменов.
Не формально: отношение (relationship) – зависимость
одних данных от других
Например,
R = {(2,1), (4,1)}
D1 D2 = {(2,1), (2,3) , (2,5) , (4,1) , (4,3) , (4,5)}
D1 x D2
D2
R
D1

18. Характеристики отношения

Отношение моделирует реальную ситуацию, т.е. для
каждого элемента из R можно утверждать, что он
соответствуют действительности
Фамилия
студента :
фамилия
Учебная
дисциплина :
дисциплина
Экзаменационная оценка :
оценка
Иванов
Петров
Петров
СПО
БД
СПО
2
4
5
Кортеж = Строка = n-ка
Атрибут - вхождение домена в отношение
Степень отношения – количество атрибутов
Кардинальность – количество кортежей
Схема отношения – перечень имен атрибутов с
указанием соответствующих доменов

19. Свойства отношения

В отношении нет двух одинаковых
кортежей
Порядок следования кортежей –
произвольный
Атрибуты имеют уникальные имена
Пример атрибутов из одного домена
R = <Фамилия студента : Фамилия, Год рождения : Год, Год поступления : Год>

20. Свойства отношения

Если атрибуты из одного домена, то они называются
-сравнимыми, где - множество операций
сравнения для заданного домена. Например, место
рождения и место жительства – сравнимы, место
рождения и год рождения не сравнимы (разные
домены).
Для домена «Год рождения» = {=, <>, >, <, >=, <=}
Для домена «Место жительства» = {=, <>}
Эквивалентные схемы – одинаковая степень и
одинаковый порядок следования атрибутов

21. Реляционные ключи

Реляционная модель данных – совокупность взаимосвязанных
отношений. Для поддержки иерархических связей
предназначены ключи.
Суперключ – атрибут или множество атрибутов, однозначно
определяющие кортеж данного отношения.
Потенциальный ключ – суперключ, который не содержит
подмножества, также являющегося суперключем данного
отношения. Т.о. потенциальный ключ обладает свойствами
уникальности и неприводимости.
Первичный ключ – это потенциальный ключ, который выбран
для уникальной идентификации кортежей внутри отношения
Внешний ключ – это атрибут или множество атрибутов одного
отношения, которые принимают значения потенциального
ключа другого отношения (может быть и того же)
На схемах названия атрибутов первичного ключа выделяют подчеркиванием

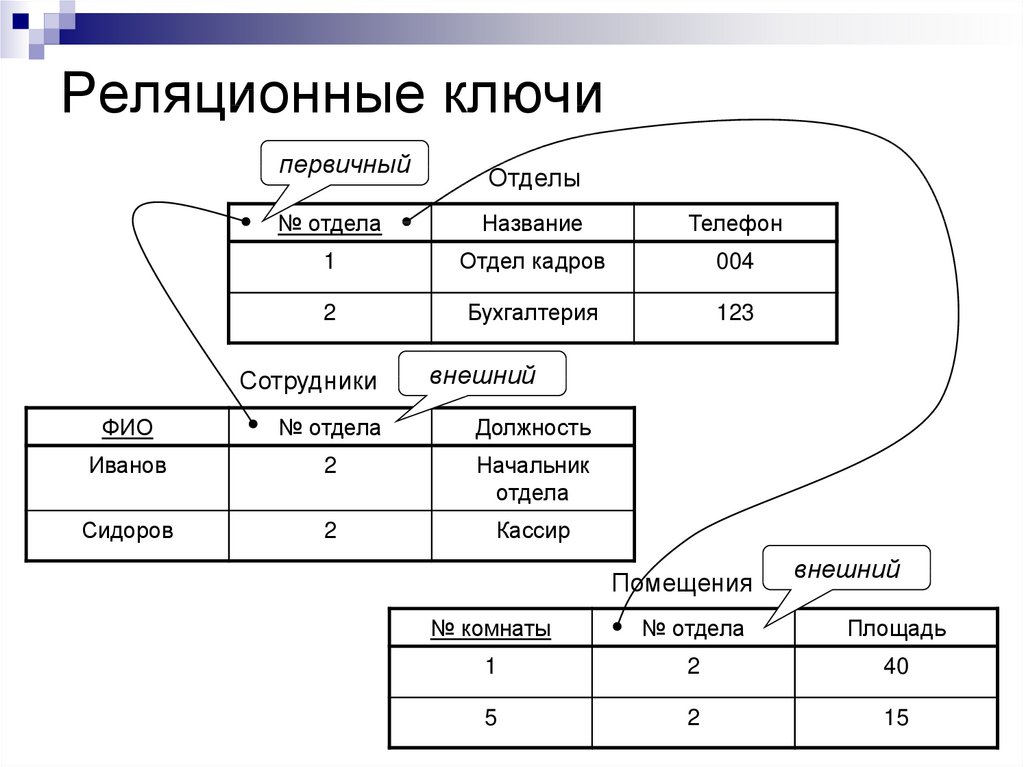
22. Реляционные ключи

первичный
Отделы
№ отдела
Название
Телефон
1
Отдел кадров
004
2
Бухгалтерия
123
Сотрудники
внешний
ФИО
№ отдела
Должность
Иванов
2
Начальник
отдела
Сидоров
2
Кассир
Помещения
внешний
№ комнаты
№ отдела
Площадь
1
2
40
5
2
15

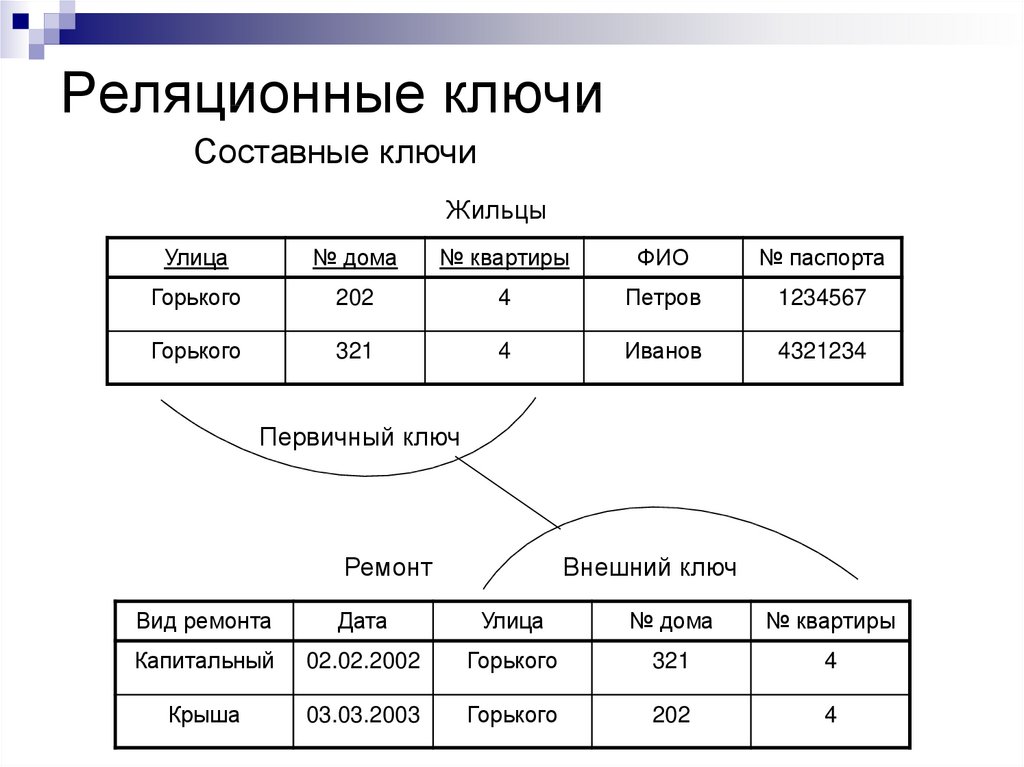
23. Реляционные ключи

Составные ключи
Жильцы
Улица
№ дома
№ квартиры
ФИО
№ паспорта
Горького
202
4
Петров
1234567
Горького
321
4
Иванов
4321234
Первичный ключ
Ремонт
Внешний ключ
Вид ремонта
Дата
Улица
№ дома
№ квартиры
Капитальный
02.02.2002
Горького
321
4
Крыша
03.03.2003
Горького
202
4

24. Реляционная алгебра

Алгебра – множество элементов с заданной на нем
совокупностью операций, замкнутых относительно
этого множества
Реляционная алгебра – множество отношений и
совокупность операций над отношениями
Реляционная база данных – совокупность некоторого
числа отношений
Концептуальная модель базы данных
(концептуальная схема базы данных) – множество
всех реляционных схем отношений

25. Теоретико-множественные операции

Объединение отношений: R1 R2 = {r | r R1 r R2}
Пересечение отношений: R1 R2 = {r | r R1 r R2}
Разность отношений: R1 \ R2 = {r | r R1 r R2}
Декартово произведение отношений (моделирует
ситуацию всех возможных исходов некоторого события):
R1 R2 = {(r1,r2) | r1 R1, r2 R2}
Операции объединения, пересечения и вычитания определены только для
отношений с эквивалентными схемами
R1
R1
R1 \ R2
R1 R2
R1 R2
R2
R1
R2
R2
R1={1,3,5,6} R2={1,6,9} R1 R2={1,3,5,6,9} R1 R2={1,6} R1\R2={3,5}

26. Теоретико-множественные операции

Примеры
R1 = <ФИО, № зач.кн> - студенты, сдававшие экзамен в первый день
R2 = <ФИО, № зач.кн> - студенты, сдававшие экзамен во второй день
R3 = <ФИО, № зач.кн> - студенты, перешедшие на следующий курс
Студенты, сдававшие экзамен 2 раза, но отчисленные
R=(R1 R2)\R3
Студенты, сдававшие экзамен 1 раз, и сдавшие его
R=((R1\ R2) R3) ((R2\ R1) R3)
R1 (фамилии)
Иванов
001
Петров
002
Сидоров
R1 R2
R2 (номера зач.кн.)
Иванов
Иванов
Петров
Петров
Сидоров
Сидоров
001
002
001
002
001
002

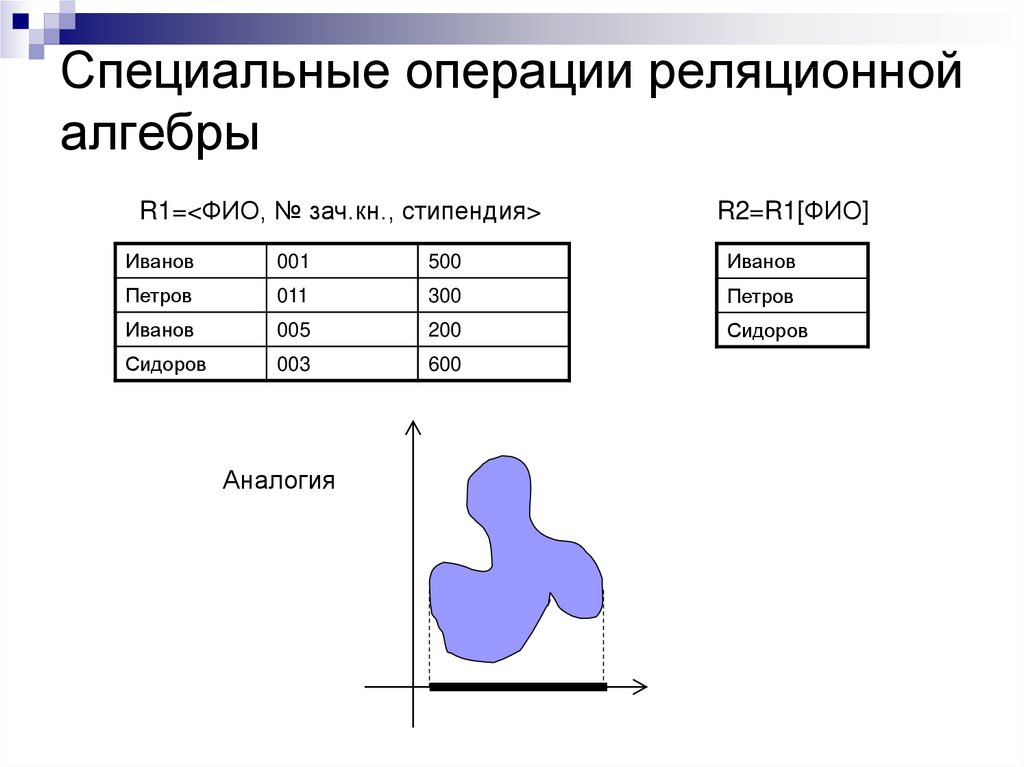
27. Специальные операции реляционной алгебры

Горизонтальная выборка (фильтрация, выборка)
R[ (r)]={r | r R (r)=истина}
где (r) – предикат от атрибутов отношения
R1=<ФИО, № зач.кн., стипендия>
R2=R1[ФИО=‘Иванов’]
Иванов
001
500
Иванов
001
500
Петров
011
300
Иванов
005
200
Иванов
005
200
Сидоров
003
600
Одноместная (унарная) операция

28. Специальные операции реляционной алгебры

Проекция
R=<a1, a2, … am>, B {ai} – множество атрибутов
R[B]={r[B]} – отношение с атрибутами B
Проекция – отношение со схемой B, содержащее кортежи
из исходного отношения, после удаления атрибутов, не
входящих в B. Дубликаты кортежей из результата
удаляются
Одноместная (унарная) операция

29. Специальные операции реляционной алгебры

R1=<ФИО, № зач.кн., стипендия>
R2=R1[ФИО]
Иванов
001
500
Иванов
Петров
011
300
Петров
Иванов
005
200
Сидоров
Сидоров
003
600
Аналогия

30. Специальные операции реляционной алгебры

Условное соединение
Двуместная (бинарная) операция
R = <a1, a2, …>
T = <b1, b2, …>
k {<, >, <=, >=, =, <>} - операции сравнения
={R.ai k T.bj}, k=1, km – предикат сравнения,
определенный для атрибутов отношений
Тогда
R[ ] = {(r,t) | r R, t T и (r.ai k t.bj)=истина, k=1,km)
Условное соединение – конкатенация кортежей по заданному условию
(поэтому условное соединение)
Операция соединения эквивалентна операции декартова произведения и
последующей выборке в соответствии с предикатом соединения

31. Специальные операции реляционной алгебры

Частные случаи условного соединения:
Соединение по эквивалентности. Это соединение в
котором все k – операции сравнения на равенство
Естественное соединение. Это соединение по
эквивалентности двух отношений R и T, выполняемое
по общим атрибутам X, из результатов которого
исключаются по одному экземпляру каждого общего
атрибута
Внешние соединения. (Будут рассмотрены позже)
R2
R1
x
y
y
R1[R1.y=R2.y]R2
z
x
y
y
z
x
y
z
a
1
1
H
a
1
1
H
a
1
H
b
2
1
C
a
1
1
C
a
1
C
3
N
Соединение
по эквивалентности
Естественное
соединение

32. Примеры

Концептуальная схема базы данных
E =<ФИО, Дисц, Оценка> - результаты сдачи
экзаменов
G=<ФИО, Группа> - состав группы
P=<Группа, Дисц> - набор дисциплин, по
которым надо сдавать экзамены группам
1. Получить список студентов, сдавших на
отлично БД
R = ( E[Оценка=5 и Дисц=‘БД’] )[ФИО]

33. Примеры

2. Получить список тех, кто должен был сдавать
экзамен по БД, но пока еще не сдавал
а) Соединить G и P, чтобы получить студентов и
дисциплины, которые они должны сдавать
R1 = (G[G.Группа = P.Группа и P.Дисц = ‘БД’]P) [ФИО]
б) Получить студентов, сдавших экзамен по БД
R2 = (E[E.Дисц=‘БД’])[ФИО]
в) Вычесть из всех, кто должен сдавать тех, кто уже
сдал
R = R1\R2

34. Примеры

3. Получить список студентов, имеющих несколько
двоек (более одной)
Введем E’ – ссылка на то же самое отношение E
(переименование отношения).
R = (E[E.ФИО=E’.ФИО и E.Оц=E’.Оц и E.Оц=2 и
E.Дисц<>E’.Дисц]E’)[ФИО]
E’
E
ФИО
Дисц
Оценка
ФИО
Дисц
Оценка
Иванов
БД
2
Иванов
БД
2
Петров
БД
4
Петров
БД
4
Иванов
ОС
2
Иванов
ОС
2

35. Примеры

4. Получить список круглых отличников
а) Получить список студентов, которые должны что-либо сдавать с
соответствующими дисциплинами
R1=(G[G.Группа=P.Группа]P [ФИО, Дисц]
б) Получить список студентов и дисциплин, уже сданных на отлично.
Но среди студентов будут еще те, которые не все сдали на отлично
или что-то еще не сдали.
R2 = (E[Оценка=5])[ФИО, Дисц]
в) Список студентов, что-либо не сдавших на отлично, или не сдавших
какие-то экзамены
R3 = (R1\R2)[ФИО]
г) Из всех студентов вычесть не сдавших что-либо на отлично и не
сдававших какие-то экзамены
R = R1[ФИО]\R3
(здесь нельзя делать G[ФИО]\R3, т.к. в результат попадут студенты,
которые не должны сдавать экзамены вообще)

36. Примеры

Концептуальная модель производства деталей
P=<Шифр, Название> - номенклатура деталей
D=<Цех> - все цеха завода
F=<Шифр, Цех> - детали, выпускаемые цехами
5. Определить перечень цехов, в которых выпускаются все
детали (вся номенклатура)
R1 = P[Шифр] получить шифры всех деталей
R2 = R1xD моделируется ситуация, когда во всех цехах выпускаются
все детали
R3 = R2\F остаются цеха и детали, не выпускаемые в этих цехах
R4 = R3[Цех] цеха, в которых выпускаются не все детали
R5 = D\R4 цеха, в которых выпускаются все детали