Похожие презентации:
Лекция 6. Сетевые методы и графы в автоматизированном управлении
1. Лекция 6 – по курсу «Сетевые методы и графы в автоматизированном управлении»
Алгоритмы,формулы и рисунки2.
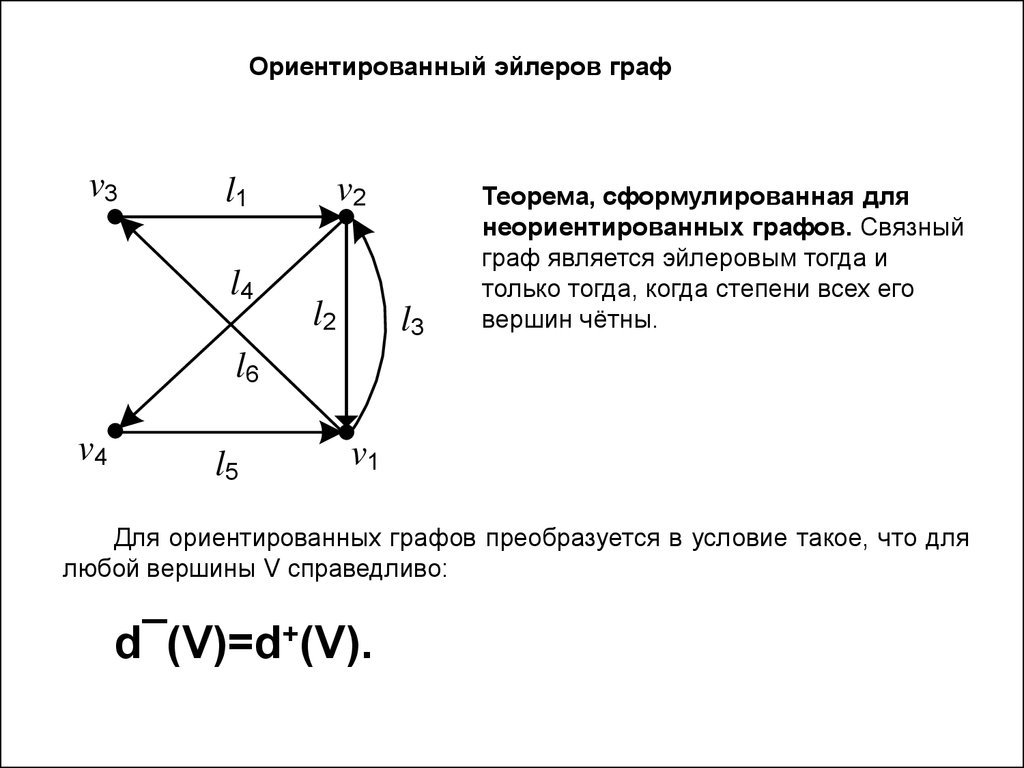
Ориентированный эйлеров графv3
v2
l1
l4
l2
l3
Теорема, сформулированная для
неориентированных графов. Связный
граф является эйлеровым тогда и
только тогда, когда степени всех его
вершин чётны.
l6
v4
l5
v1
Для ориентированных графов преобразуется в условие такое, что для
любой вершины V справедливо:
d¯(V)=d+(V).
3.
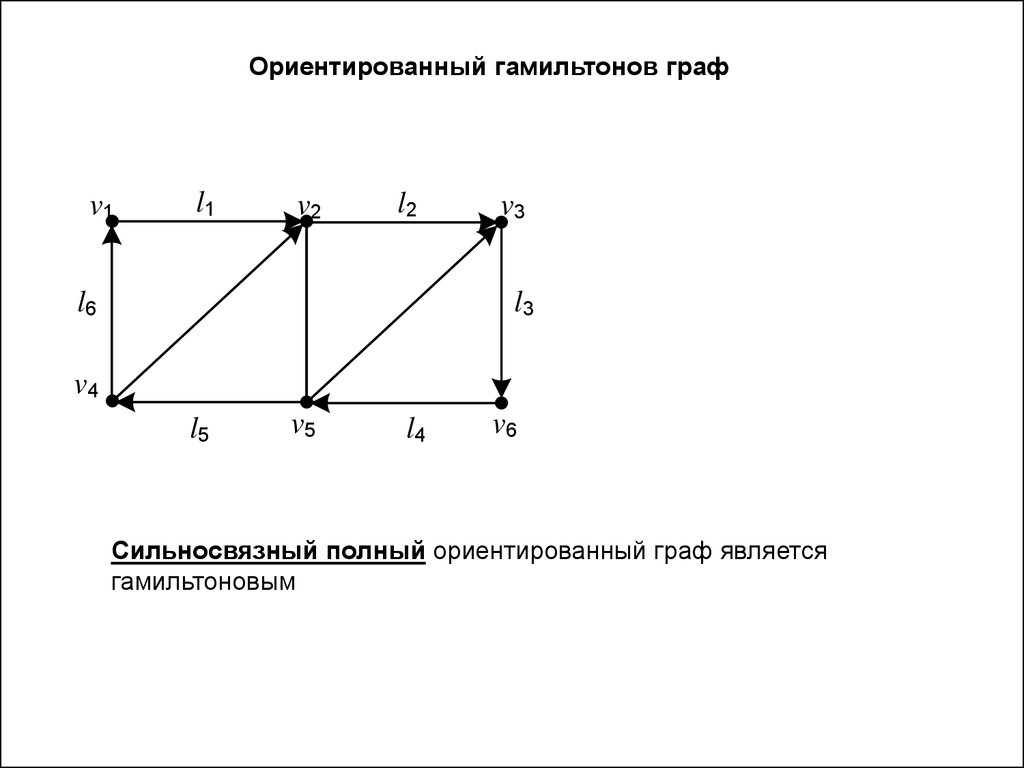
Ориентированный гамильтонов графv1
l1
v2
l2
l6
v3
l3
v4
l5
v5
l4
v6
Сильносвязный полный ориентированный граф является
гамильтоновым
4.
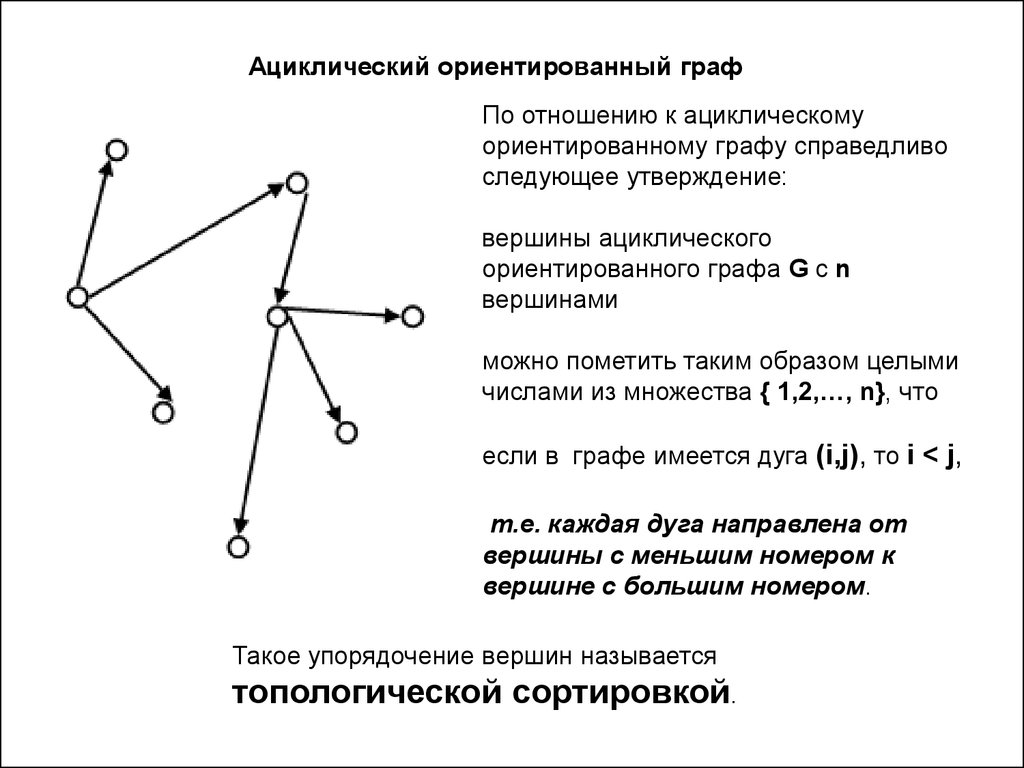
Ациклический ориентированный графПо отношению к ациклическому
ориентированному графу справедливо
следующее утверждение:
вершины ациклического
ориентированного графа G с n
вершинами
можно пометить таким образом целыми
числами из множества { 1,2,…, n}, что
если в графе имеется дуга (i,j), то i < j,
т.е. каждая дуга направлена от
вершины с меньшим номером к
вершине с большим номером.
Такое упорядочение вершин называется
топологической сортировкой.
5.
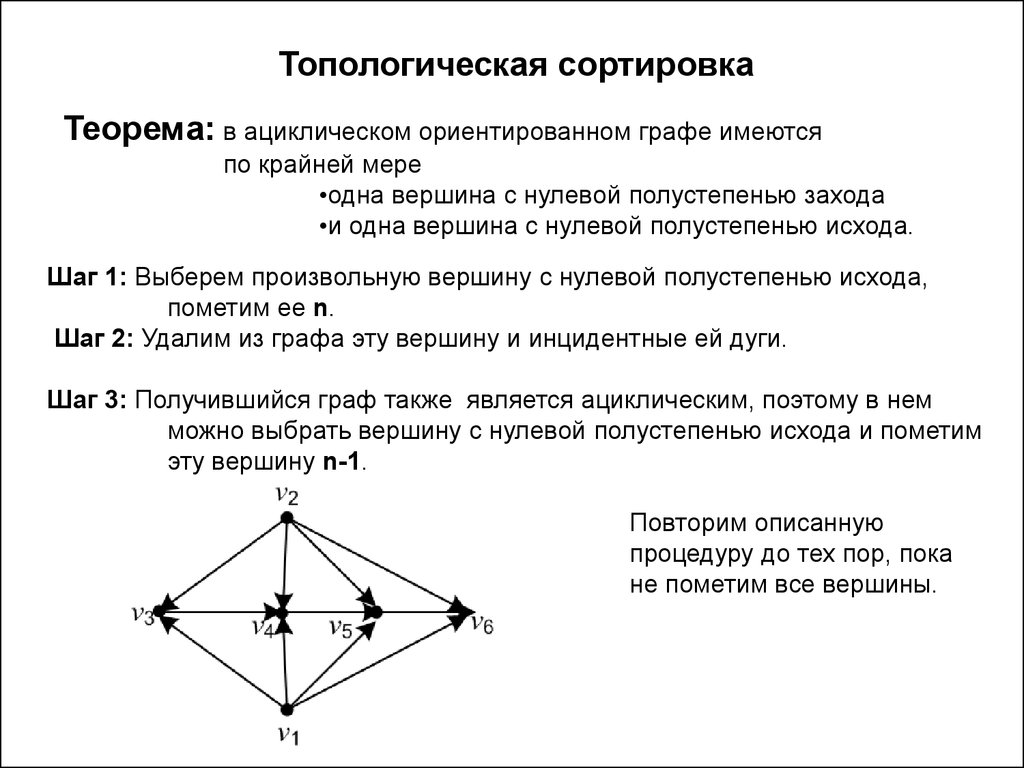
Топологическая сортировкаТеорема: в ациклическом ориентированном графе имеются
по крайней мере
•одна вершина с нулевой полустепенью захода
•и одна вершина с нулевой полустепенью исхода.
Шаг 1: Выберем произвольную вершину с нулевой полустепенью исхода,
пометим ее n.
Шаг 2: Удалим из графа эту вершину и инцидентные ей дуги.
Шаг 3: Получившийся граф также является ациклическим, поэтому в нем
можно выбрать вершину с нулевой полустепенью исхода и пометим
эту вершину n-1.
Повторим описанную
процедуру до тех пор, пока
не пометим все вершины.
6.
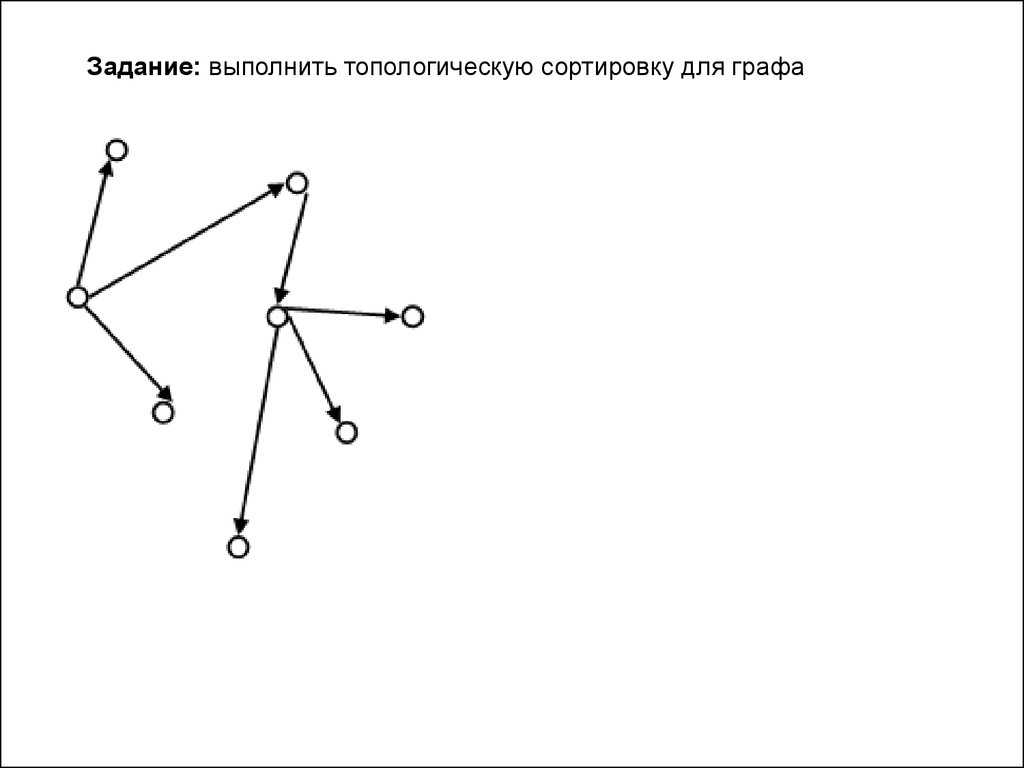
Задание: выполнить топологическую сортировку для графа7.
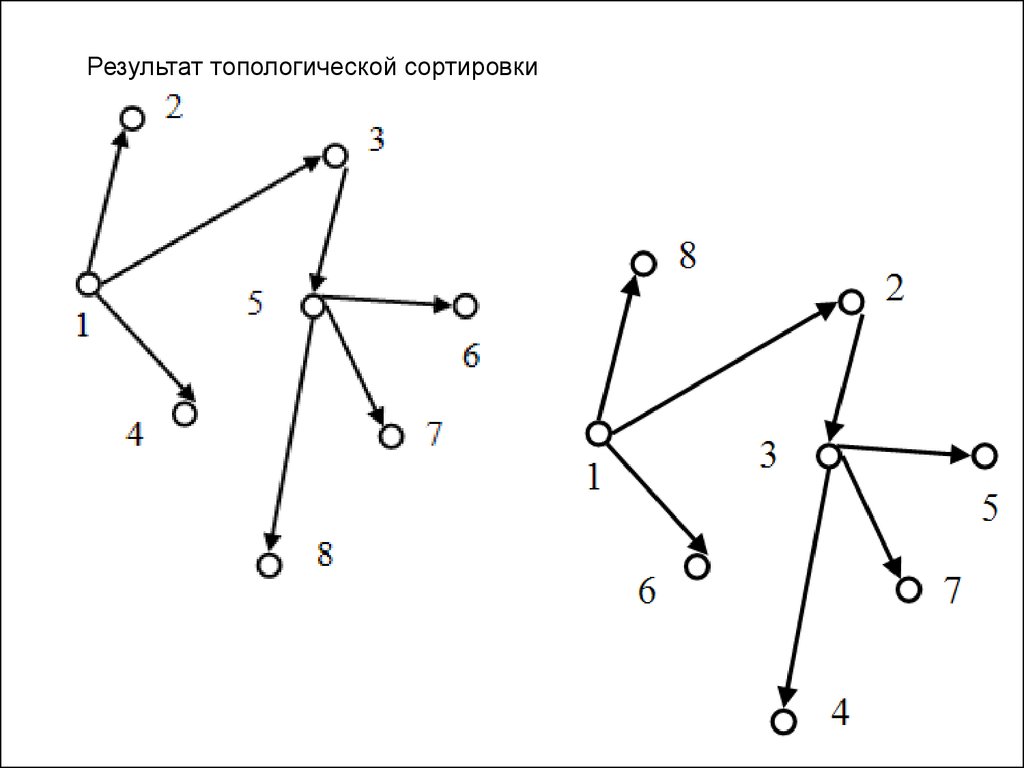
Результат топологической сортировки8.
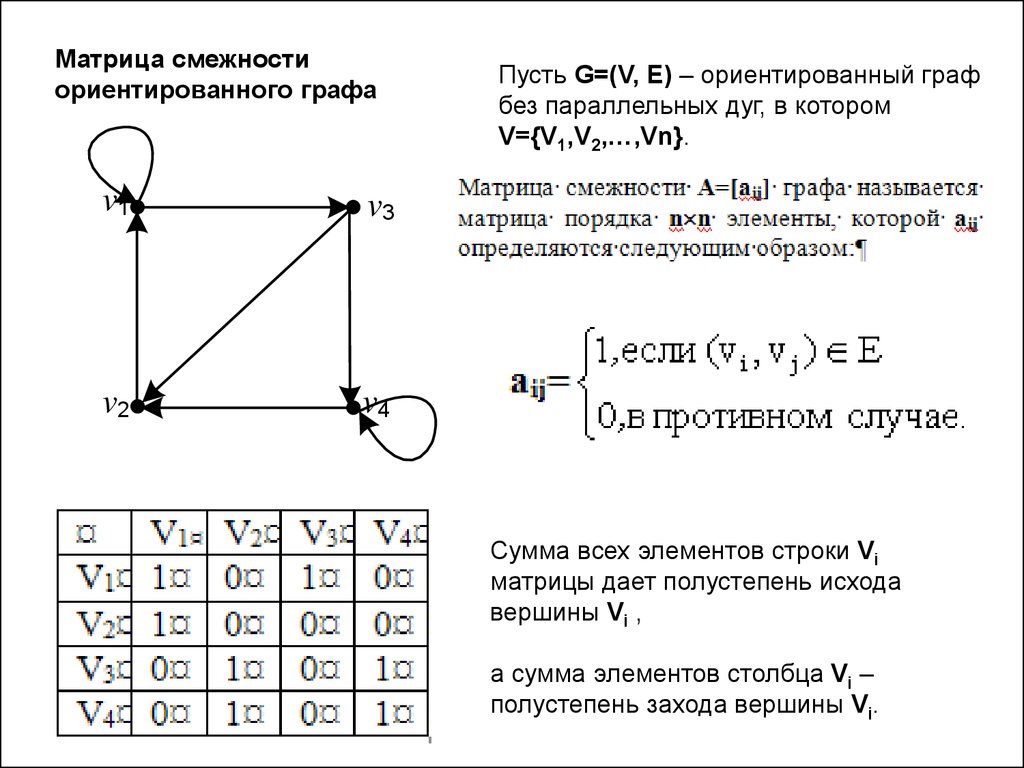
Матрица смежностиориентированного графа
v1
v3
v2
v4
Пусть G=(V, E) – ориентированный граф
без параллельных дуг, в котором
V={V1,V2,…,Vn}.
Сумма всех элементов строки Vi
матрицы дает полустепень исхода
вершины Vi ,
а сумма элементов столбца Vi –
полустепень захода вершины Vi.
9.
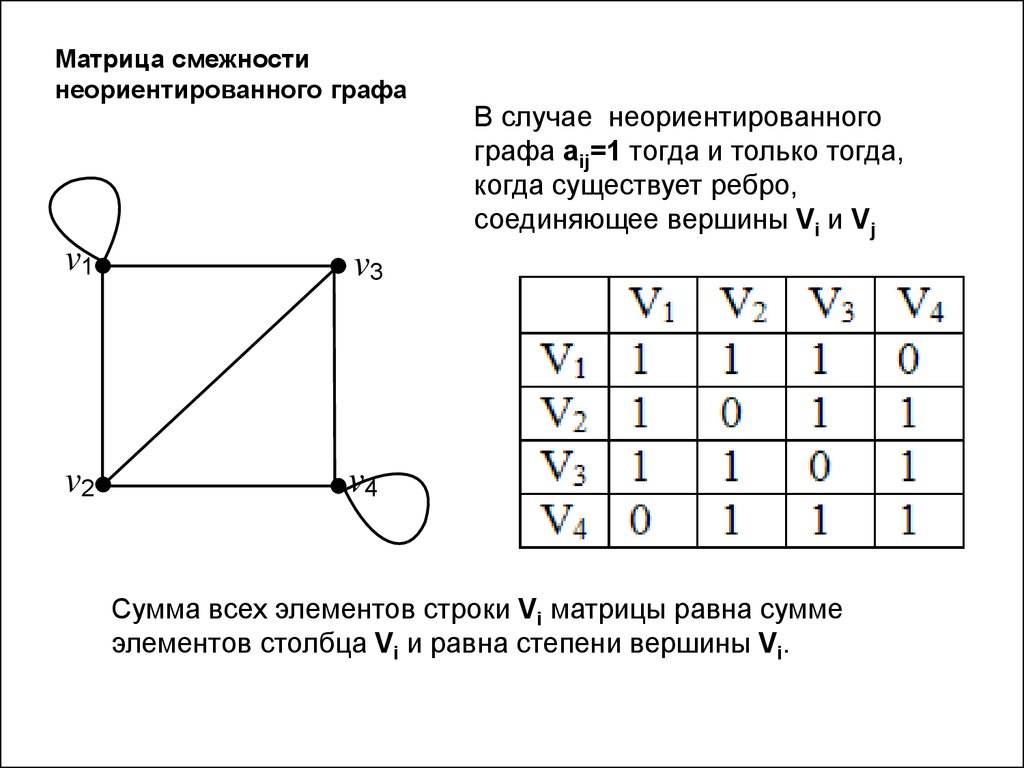
Матрица смежностинеориентированного графа
v1
v3
v2
v4
В случае неориентированного
графа aij=1 тогда и только тогда,
когда существует ребро,
соединяющее вершины Vi и Vj
Сумма всех элементов строки Vi матрицы равна сумме
элементов столбца Vi и равна степени вершины Vi.
10.
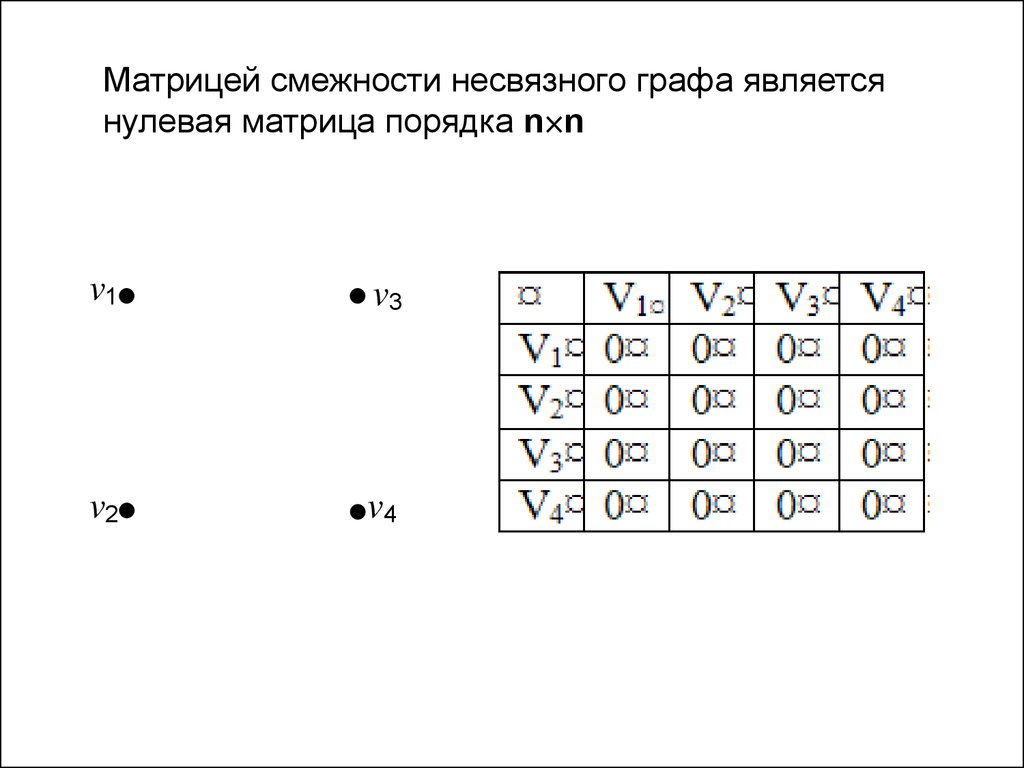
Матрицей смежности несвязного графа являетсянулевая матрица порядка n n
v1
v3
v2
v4
11.
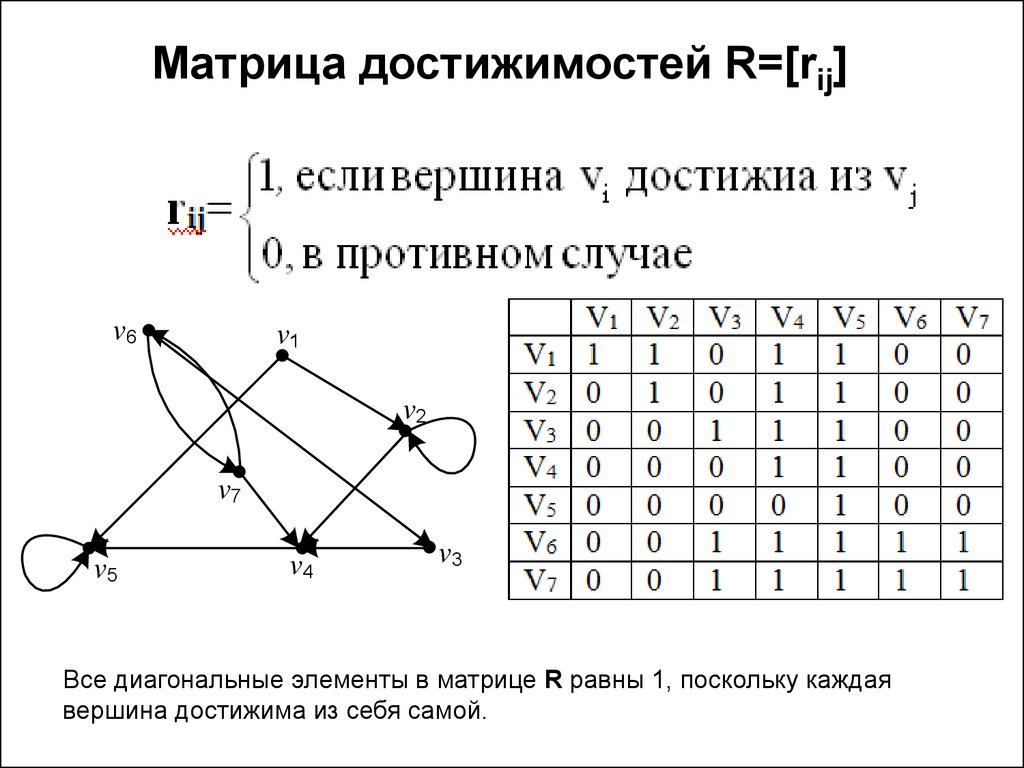
Матрица достижимостей R=[rij]v6
v1
v2
v7
v5
v4
v3
Все диагональные элементы в матрице R равны 1, поскольку каждая
вершина достижима из себя самой.
12.
Вопрос 1.Как будет выглядеть матрица
достижимости для неоринтированного графа?
Вопрос 2.
Как будет выглядеть матрица
достижимости для несвязного графа?
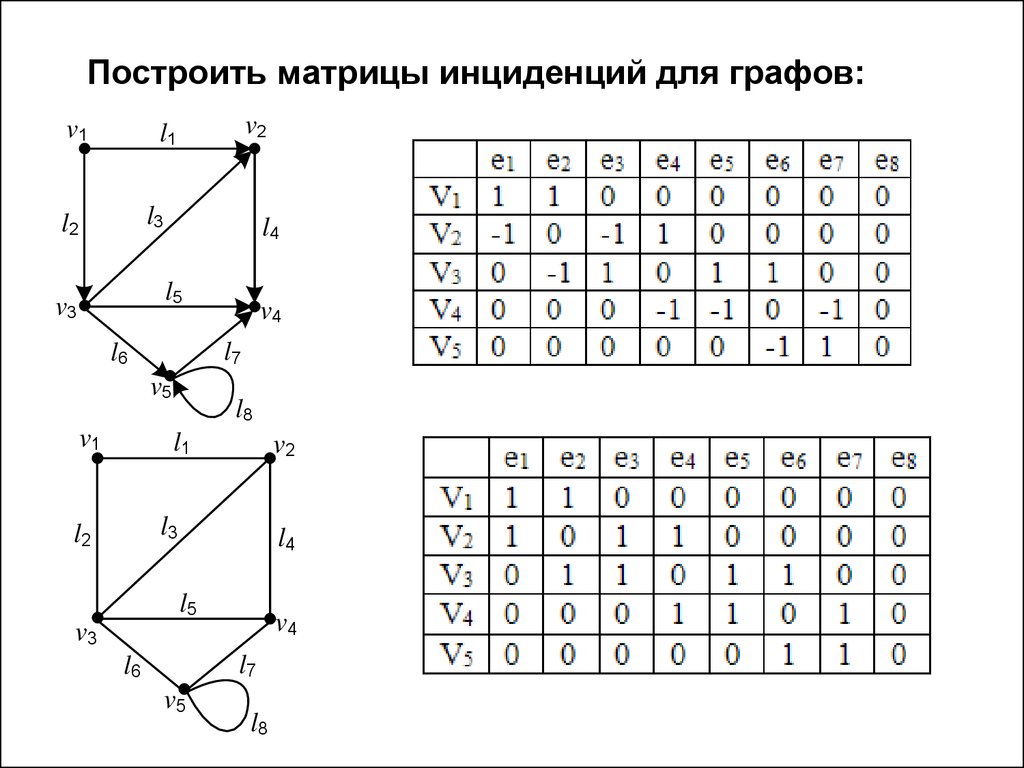
13. Матрица инциденций B=[bij]
Рассмотрим граф G на n вершинах и m ребрахЕсли граф G ориентированный
Если граф G неориентированный
14.
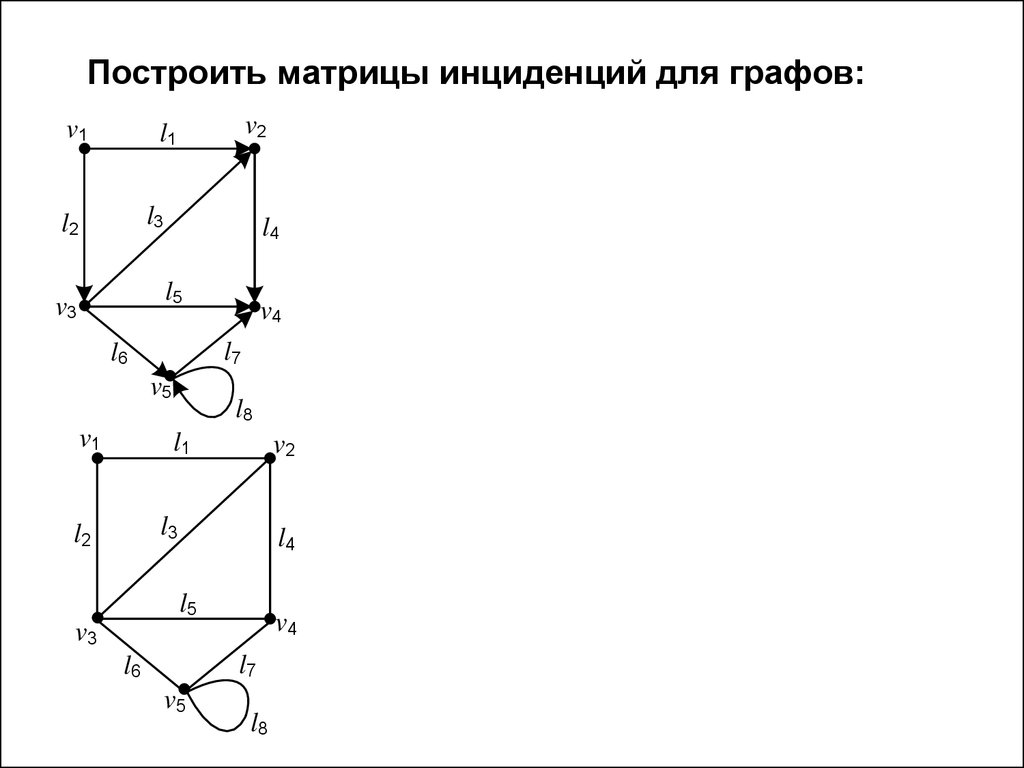
Построить матрицы инциденций для графов:v1
v2
l1
l3
l2
l4
l5
v3
l7
l6
v5
v1
v4
l8
l1
v2
l3
l2
l4
l5
v4
v3
l7
l6
v5
l8
15.
Построить матрицы инциденций для графов:v1
v2
l1
l3
l2
l4
l5
v3
l7
l6
v5
v1
v4
l8
l1
v2
l3
l2
l4
l5
v4
v3
l7
l6
v5
l8
16.
Свойства матриц инциденций для графов:Свойства матрицы инцидентности
неориентированного графа.
1. Сумма элементов матрицы на i-й
строке равна степени вершины i.
2. Сумма элементов матрицы по i-му
столбцы равна 2.
Свойства матрици инцидентности
орграфа.
1. Сумма строк матрицы B(G) является
нулевой строкой.
2. Любая строка матрицы B(G) является
линейной комбинацией остальных строк.
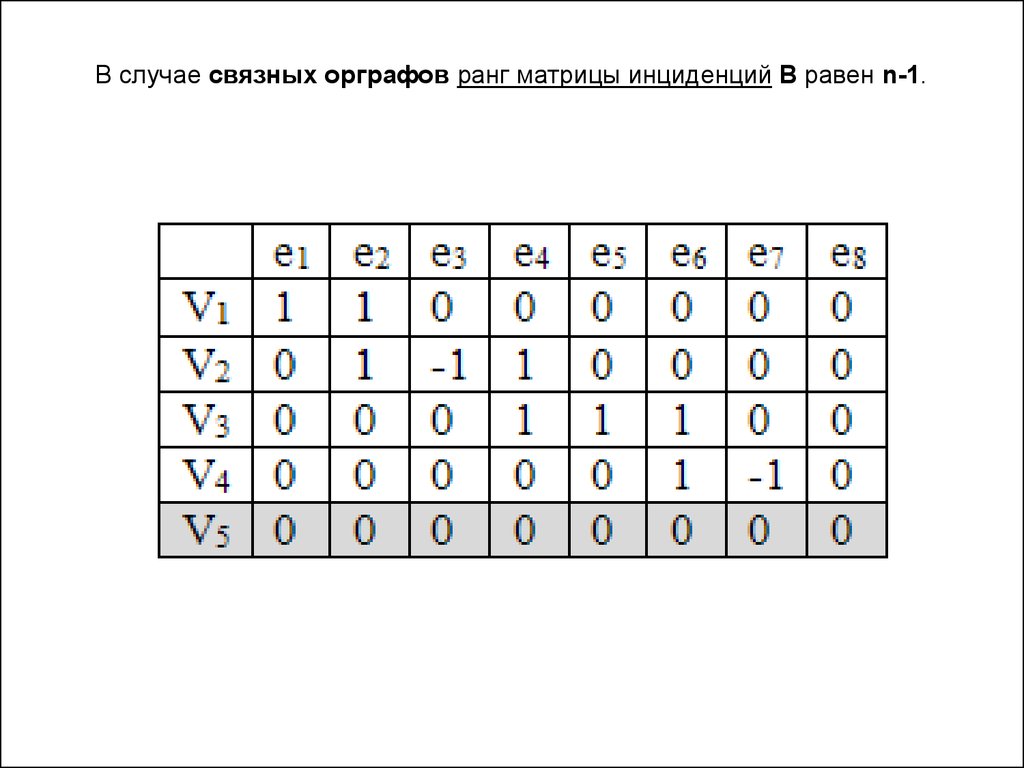
3. Ранг матрицы B(G) равен p-1.
17.
В случае связных орграфов ранг матрицы инциденций В равен n-1.18.
Построить матрицы инциденций для графов:v1
l2
v3
l1
v2
l3
l4
l5
v5
v4
l8
v1
l2
l1
v2
l3
l4
l5
v4
v3
v5
l8
19.
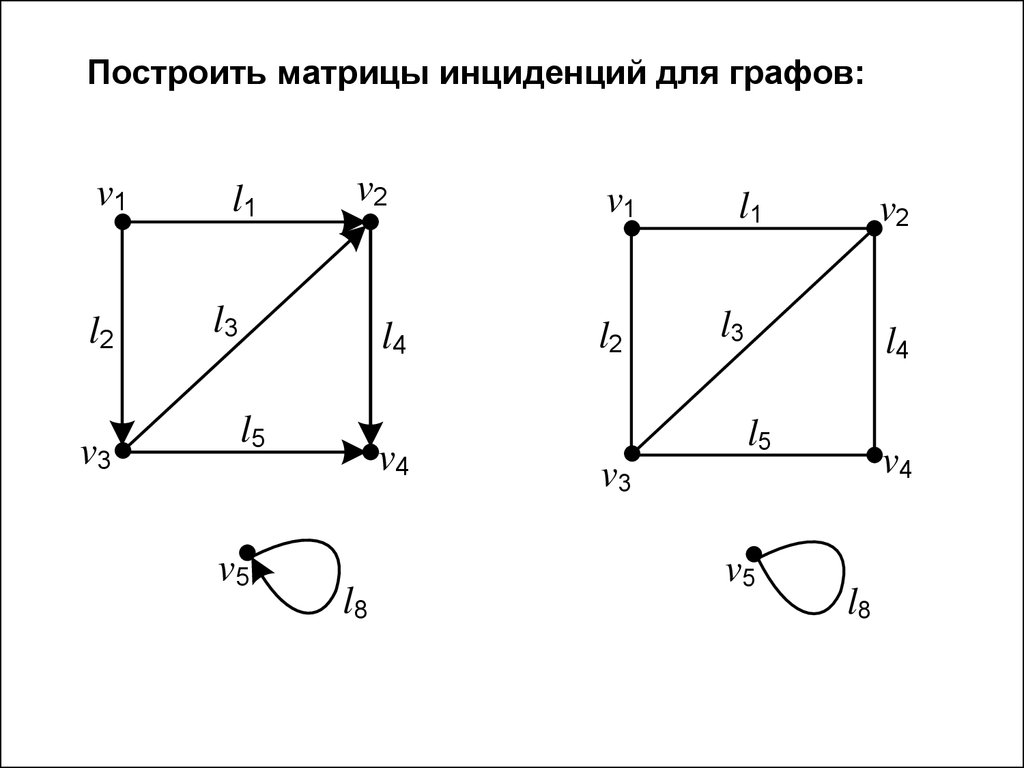
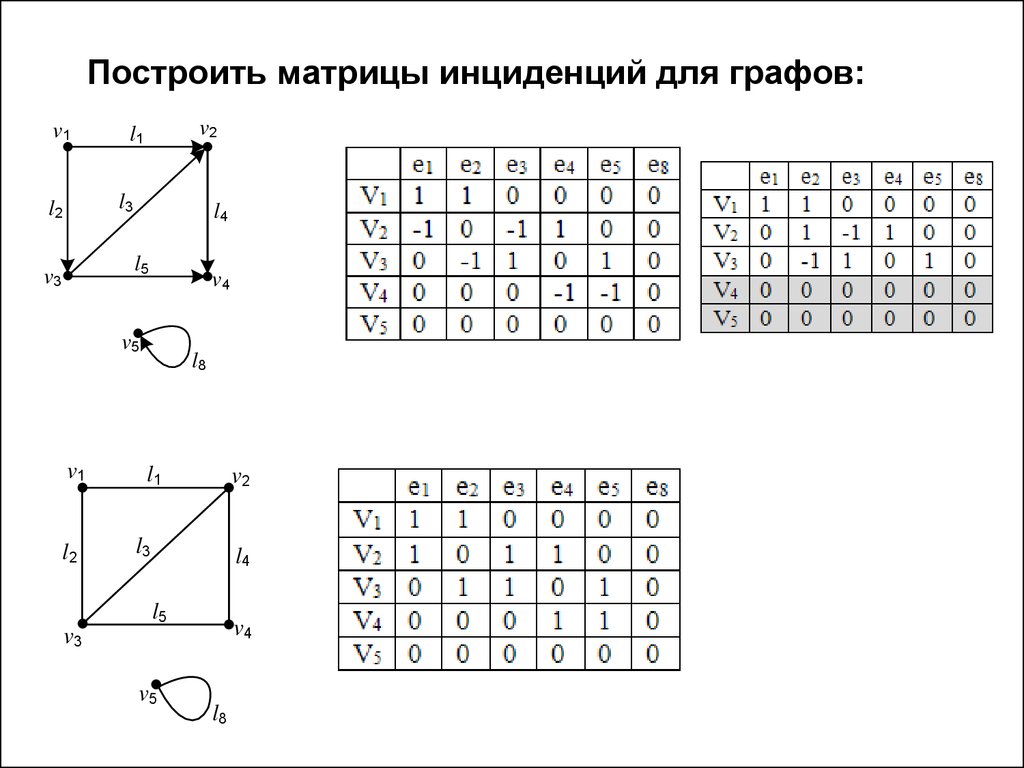
Построить матрицы инциденций для графов:v1
v2
l1
l3
l2
l4
l5
v3
v4
v5
v1
l2
l8
l1
v2
l3
l4
l5
v4
v3
v5
l8


![Матрица инциденций B=[bij] Матрица инциденций B=[bij]](https://cf.ppt-online.org/files/slide/x/XnJP5zZgfHyCoi0w9rBL24v3t6DYasjxKVcueT/slide-12.jpg)

 Информатика
Информатика








