Физико-математические основы ландшафтоведения (Часть II)

1. Географический факультет Московского государственного университета им. М.В.Ломоносова [email protected]

Сысуев В.В.
доктор географических наук, профессор
ФИЗИКО-МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ЛАНДШАФТОВЕДЕНИЯ
(Часть II)
Географический факультет
Московского государственного университета им. М.В.Ломоносова
[email protected]

2. ЭТАПЫ РАЗРАБОТКИ ТЕОРИИ ГЕОСИСТЕМ

1.Систематизация структурообразующих геосистемных процессов
Радиальные процессы
формирования
элементарных геосистем
Латеральное сопряжение
геосистем элементарного
водосбора
Формирование структуры
геосистем высоких
иерархических порядков
2.Формализация пространственной структуры геосистем
Элементарные геосистемы:
земная поверхность в поле гравитации
(конвергенция-дивергенция и ускорениезамедление потоков) и
в поле инсоляции (освещенность, доза
солнечной радиации и др.)
Параметры структуры водосборов:
поверхностных - линии тока,
водоразделы, тальвеги, порядок
водосбора и др.; подземных почвенные и литологические
горизонты и линеаменты, и др.
3.Создание,верификация,идентификация моделей функционирования
Радиальные процессы переноса в элементарных геосистемах:
биогенные (продуктивность, сукцессии, малый биокруговорот );
атмогенные (радиационный, конвективно-диффузионный и др)
гидроциркуляционные (транспирация, трансформация осадков
растительностью, влагомассоперенос в почвах, и др.)
Процессы
латерального
переноса на
водосборах,
барьеры и др.

3.

1. Структурообразующие процессы в геосистемах низкого иерархического уровня
Биоциркуляционные процессы
переноса вещества и энергии
Геоциркуляционные процессы,
почвенные процессы
Латеральные процессы
сопряжения
ландшафтов
1. Фотосинтез и дыхание отдельных органов
2. Поглощение, мембранный и др. транспорт и
перераспределение элементов минерального питания и
ассимилятов внутри органов
3. Поглощение влаги и регулирование транспирации
устьичными механизмами
4. Трансформация параметров микроклимата (радиация,
ветер, температура, влажность, и т.п.) и газового
состава атмосферы внутри и под пологом растений
5. Процессы метаболизма отдельных особей и
некоторых популяций редуцентов
1. Инсоляция и процессы перераспределения и
поглощения радиации
2. Процессы газообмена в приземном слое атмосферы
3. Процессы выпадения и перераспределения твердых
и жидких атмосферных осадков
4. Метаморфизация атмосферных выпадений
биогоризонтами (ярусами растительности)
5. Вертикальный гравитационный тепло-влагоперенос и миграция растворенных веществ в почвах
1. Динамика поверхностного
склонового стока (водный, ионный,
твердый сток) за единичный процесс
2 Формы нахождения химических
веществ в водах стока
3. Биогенные процессы сопряжения:
миграция организмов и биологически
активных соединений
1. Продукционные процессы и накопление биомассы
растением в целом
2. Активные и пассивные процессы обмена растений с
почвой и атмосферой органическими и минеральными
соединениями
3. Трансформация суточного хода параметров
микроклимата, влияние на мезо климатические
процессы (шероховатость поверхности, поле ветра,
осадков и т.п., альбедо поверхности, температура,
давление масс воздуха и т.п.)
4. Динамика популяций редуцентов
1. Выпадение сухих аэрозолей
2. Формирование температурного поля и его суточной
динамики в почвах
3. Испарение, транспирация и капиллярное
сорбционное перераспределение влаги по профилю
почвы
4. Динамика рН, Еh, рХ в верхних горизонтах почв
под влиянием метаболизма
5. Сорбция-десорбция, диффузионные,
коагуляционные и др. процессы перераспределения
минеральных и органических соединений между
фазами и по профилю почвы
1. Поверхностный дождевой сток на
водосборах первых порядков
(водный, ионный, твердый сток)
2. Внутрипочвенный водный и
ионный сток
3. Динамика влажности и
влагозапасов поверхностных
горизонтов почв
4. Динамика катастрофических
процессов: пожары, ветровалы,
наводнения и т.п.
1. Фенологические фазы
2. Формирование продукции вертикальных ярусов
(биогоризонтов)
3. Перенос вещества и энергии по трофическим цепям
4. Динамика опада и накопления мертвого
органического вещества
5. Формирование специфической сезонной динамики
микроклимата
6. Динамика гетеротрофных процессов минерализации
органических веществ, накопление подстилки, торфа,
высвобождение элементов зольного состава и т.д
1. Сезонная динамика температуры почв, промерзание
– оттаивание почв
2. Динамика запасов влаги и воднорастворимых
соединений в почве и снежном покрове
3. Динамика рН – Еh условий почвенной среды и
формирование распределения по профилю
4. Почвенно-ферментативные процессы
5. Динамика содержания элементов питания в почве
6. Динамика состава поглощенных ионов в ППК
7. Реологические и термореологические процессы и
структурообразование в почвах
1. Динамика сезонного стока на
водосборах любого порядка
2. Динамика грунтового стока и
уровня грунтовых вод
3. Балансы питательных веществ и
агрохимикатов на склонах и
водосборах
4. Водно-солевые балансы по
элементам рельефа
5..Гравитационные (механические)
склоновые процессы
Годы – десятилетие
Месяц, сезон
1. Формирование продукции фитоценоза
2. Динамика свойств органогенных горизонтов почв
3. Биогеохимический круговорот углерода и зольных
элементов
4. Эндо- и экзогекнная динамика микросукцессий
1. Стадийное преобразование почвенных минералов и
коллоидов (выветривание легко разрушающихся
минералов, протонация, гидратация, кристаллизация,
матричная достройка глинных минералов и т.п.
2. Матричная достройка гумуса почв
3. Формирование микроморфологии почв
1. Линейная, площадная эрозия и
химическая денудация склонов
2. Уровенный режим рек и водоемов
стока водосборов высокого порядка
3. Пионерное заселение извне,
распространение растений
Десятилетия - века
Год, десятилетие
1. Сукцессионные смены растительности
2. Динамика формирования гумусовых, торфяных и
других органогенных горизонтов почв
3. Малый геохимический круговорот вещества
1. Формирование мезоструктуры почвенных
горизонтов (системы вертикальных трещин и
сквозных пор)
2. Формирование вертикальных почвенных морфонов
1. Формирование микро- мезорельефа
2. Формирование и динамика
деятельного слоя
3. Уровенный режим морей' и
океанов
Ближнее эволюционное
(геологическое)
Столетия, тысячелетие
Формирование структуры растительного покрова
Формирование структуры почвенного покрова
Формирование макро- и мегарельефа,
глобальные геохимические и
литогенные циклы, глобальные
циклы похолодания – потепления и
уровенный режим Мирового океана
Тип процесса
Характерное время
шаг моделирования
Час - несколько часов
Минуты
Сутки -несколько суток
Десятки минут, час
Сезон - год
Сутки, декада

4. Дифференциация ПТК по морфометрическим параметрам распределения солнечной радиации и тепла

Наиболее теплые хорошо дренируемые склоны моренных холмов
и гряд южной экспозиции c максимальной инсоляцией
Теплые дренируемые склоны моренных холмов и гряд южной и
северной экспозиций со средней
инсоляцией
Умеренно прохладные увлажненные склоны моренных холмов
южной и северной экспозиций со
средней инсоляцией
Прохладные переувлажненные
нижние части склонов холмов,
моренных гряд и террасовидных
уступов
Холодные выпуклые центральные части болот
Холодные плоские поверхности
болот
Холодные поверхности плоских
болот и слабонаклонных заболоченных поверхностей
Холодные слабонаклонных болотных поверхностей, долин речек и плоских заболоченных поверхностей холмов и террасовидных уступов
Холодные плоские заболоченных
поверхностей

5. Дифференциация ПТК по морфометрическим параметрам распределения гидрологического стока и заболачивания

Центральные выпуклые части болотных массивов
Болотные массивы (верховые, переходные, низинные),
долины речек
Плоские заболоченные вершины холмов, периферийные участки болот
Краевые части болот
Заболоченные нижние части
склонов моренных холмов и
гряд
Пологие слабо дренируемые
склоны моренных холмов и
гряд
Покатые дренируемые склоны моренных холмов и гряд
Покатые хорошо дренируемые склоны моренных холмов и гряд
Хорошо дренируемые склоны моренных холмов и гряд
Наиболее крутые (до 6о ) хорошо дренируемые склоны
моренных холмов и гряд

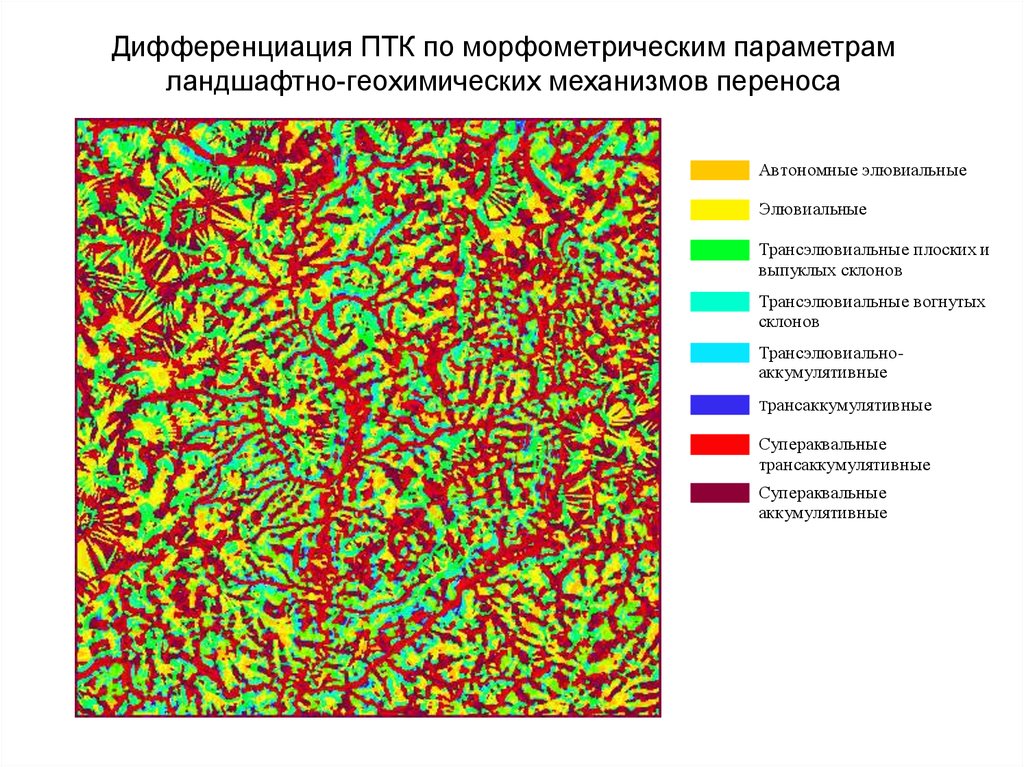
6. Дифференциация ПТК по морфометрическим параметрам ландшафтно-геохимических механизмов переноса

Автономные элювиальные
Элювиальные
Трансэлювиальные плоских и
выпуклых склонов
Трансэлювиальные вогнутых
склонов
Трансэлювиальноаккумулятивные
Трансаккумулятивные
Супераквальные
трансаккумулятивные
Супераквальные
аккумулятивные

7. Дифференциация ПТК по параметрам распределения геофизических полей.

Пологие склоны моренных холмов
и гряд южной экспозиции,
наиболее теплые, хорошо
дренируемые, трансэлювиальные
Плоские поверхности вершин
моренных холмов, гряд и
террасовидных уступов, теплые
дренируемые, элювиальные
Склоны моренных холмов и гряд
северной экспозиций, умеренно
теплые, дренируемые, трансэлювиальные
Склоны северной экспозиции
прохладные, слабодренируемые,
трансэлювиальные
Плоские поверхности болот в
ложбинах стока и котловинах,
холодные, переувлажненные,
супераквальные, трансэлювиальные и трансаккумулятивные
Плоские заболоченные
поверхности моренных холмов,
гряд и террасовидных уступов,
плоские ложбины стока, частично
с временными или постоянными
водотоками, периферийные части
верховых болот, холодные,
переувлажненные,
супераквальные
трансаккумулятивные
Долинный комплекс р. Межи с
низинным заболачиванием,
умеренно холодные,
супераквалные, аккумулятивные и
трансаккумулятивные

8. 2.2. ФУНКЦИОНАЛЬНО-ДИНАМИЧЕСКАЯ КЛАССИФИКАЦИЯ ГЕОСИСТЕМ

Функциональный подход - выявление механизмов современных
взаимодействий, объединяющих природные объекты в функционирующие как
единое целое геосистемы.
Потоки вещества и энергии высокой интенсивности обладают способностью
формировать специфический рельеф (флювиальный, гляциальный, эоловый и
т.д.), а также прямо или косвенно обусловливать распределение и численность
растений и животных, особенности почвенного покрова, воздействовать на
другие потоки. Таким образом, они образуют сферу влияния, которая и есть
геосистема . В бореальных условиях главным структурообразующим потоком
является водный сток.
Следовательно:
геосистемы различных порядков могут быть выделены в соответствии
со схемой Стралера-Философова на множестве элементов рельефа по
значениям морфометрических величин, описывающих распределения
воды в поле гравитации:
водоразделы любого порядка одновременно соответствуют локальным:
максимумам высоты h, минимумам величины удельной площади водосбора
(SCA), а также локальным максимумам kh (положительная величина);
тальвеги соответствуют локальным: минимумам высоты h, локальным
максимумам SCA, а также локальным минимумам kh (отрицательная
величина).

9. Карта структуры геосистем (слева) и гидросети верховий р. Межа [Федяева, 2003] (справа, цифры - порядок водотоков,

автоматическое выделение программы TOPAZ).

10.

Карта ландшафтной структуры геосистем [Козлов, Федяева, 2003]
Цветом показан тип растительного покрова, интенсивностью цвета - характер рельефа по градиенту увлажнения
#
# #
##
##
##
##
##
#
# #
#
#
##
#
#
#
#
##
#
#
#
# ## #
# # #
#
#
#
##
#

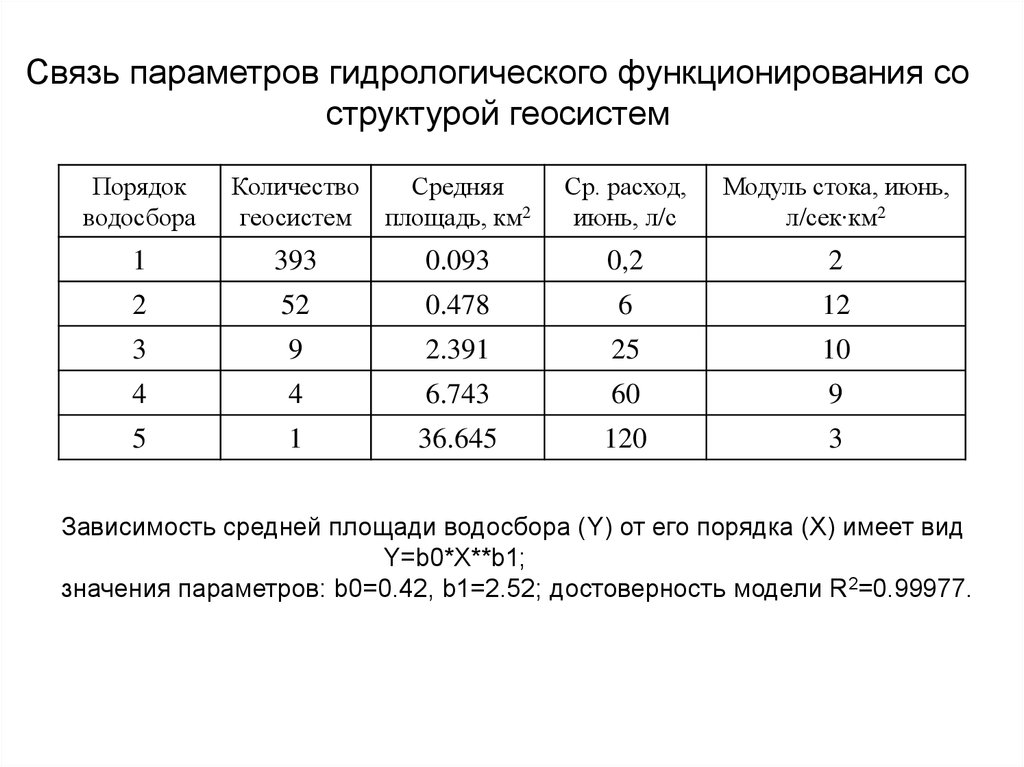
11. Связь параметров гидрологического функционирования со структурой геосистем

Порядок
водосбора
Количество
Средняя
геосистем площадь, км2
Ср. расход,
июнь, л/с
Модуль стока, июнь,
л/сек∙км2
1
393
0.093
0,2
2
2
52
0.478
6
12
3
9
2.391
25
10
4
4
6.743
60
9
5
1
36.645
120
3
Зависимость средней площади водосбора (Y) от его порядка (X) имеет вид
Y=b0*X**b1;
значения параметров: b0=0.42, b1=2.52; достоверность модели R2=0.99977.

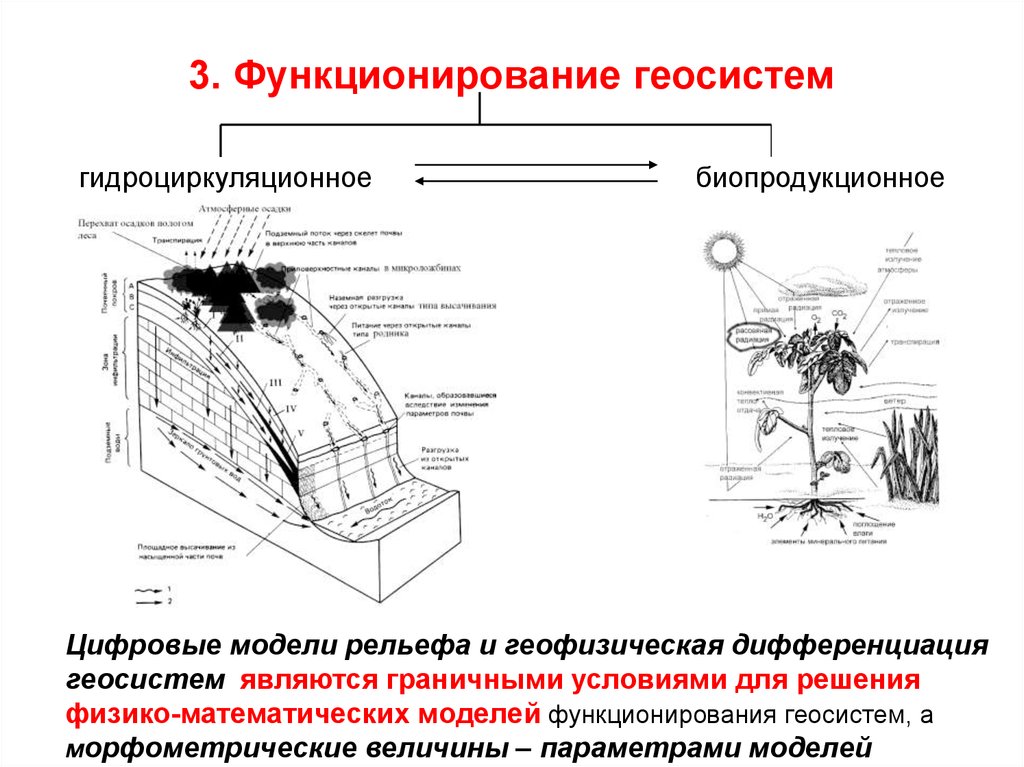
12. 3. Функционирование геосистем гидроциркуляционное биопродукционное

Цифровые модели рельефа и геофизическая дифференциация
геосистем являются граничными условиями для решения
физико-математических моделей функционирования геосистем, а
морфометрические величины – параметрами моделей

13. Методология построения физико-математических моделей (на примере гидроциркуляционного функционирования геосистем)

• материальные
точки (частицы)
• абсолютно твердое тело
• состояние физической системы
• осреднение турбулентного потока в смысле
( масса частиц mi, координаты х, у, z
и компоненты скорости vx , vy , vz
в заданный момент времени t)
• параметры
сплошной среды (в переменных Эйлера)
• система уравнений Рейнольдса (для несжимаемой жидкости )
• модель двумерного стекания воды по поверхности
водосбора (интегрировании системы уравнений Рейнольдса [Кучмент, 1983])
dm
v
dx
• уравнение неразрывности (закон сохранения)
q q( x, t ) v
• закон
движения системы частиц
(закон Ньютона)
• уравнения движения вязкой жидкости (система
уравнений Навье-Стокса для несжимаемой жидкости)
• система уравнений Сен-Венана
•уравнение кинематической волны

14.

Уравнение неразрывности - закон сохранения вещества
qm dt
dm=ρdx
х
(qm+ x qm)dt
(х+dx)
Приращение массы на отрезке среды от х до х+dx равна разности потоков:
t (dm) qm dt (qm x qm )dt x qm dt
Делим на dt·dx обе части уравнения и переносим в одну сторону
qm dm
0
x t dx
q
0
t x
или
v
0
t
x
v
v
0
x
x t
Применяя оператор пространственного дифференцирования для
трехмерного случая:
div v 0
v v 0
v grad div v = 0
t
t
t

15.

- число частиц в точке jh в момент nτ
Тогда в следующий момент при равновероятном перемещении частиц
t
(n+2)τ
(n+1)τ
nτ
τ
{0
{
(n-1)τ
h
x
(j-1)h
jh
(j+1)h
К выводу уравнения диффузии (градиентные законы)

16.

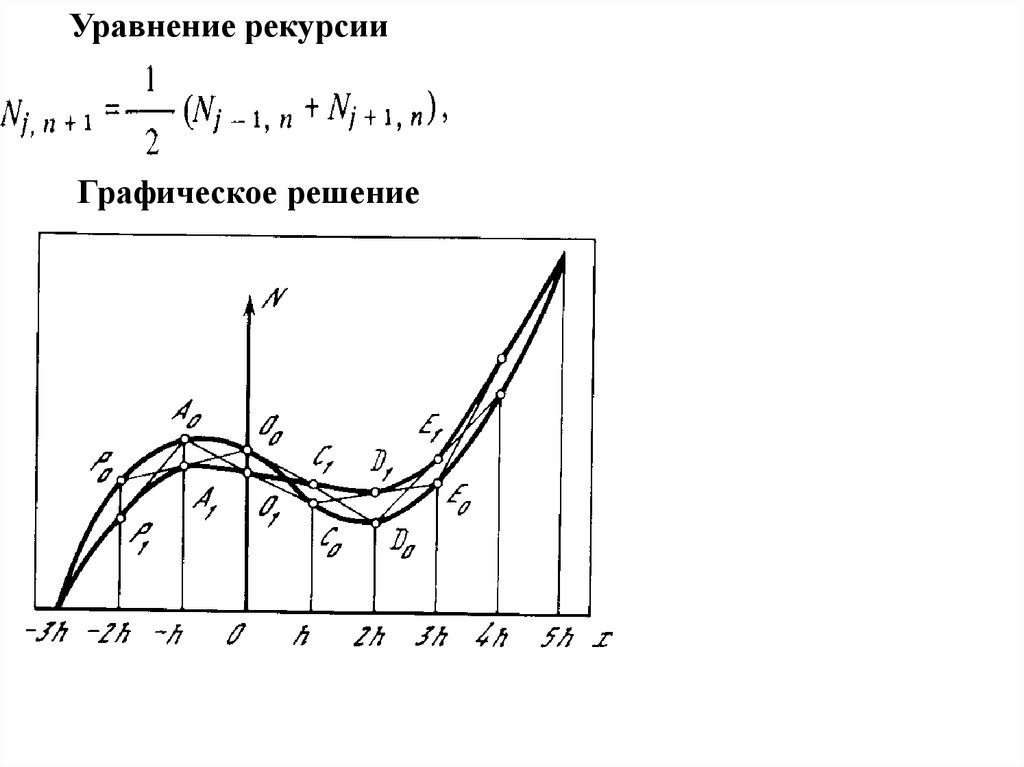
Уравнение рекурсии
Графическое решение

17.

- число частиц в точке jh в момент nτ
При перемещении частиц через точку х=(j+1/2)h в момент t =(п+1/2) в
положительном направлении переместится за единицу времени (Nj, n-Nj+1, n) 2
t
частиц , если масса каждой точки m0? то переместиться вещества:
(n+2)τ
(n+1)τ
nτ
(n-1)τ
{0
x
{
τ
h
(j-1)h
jh
(j+1)h

18.

Уравнения диффузии и дисперсии
Первый закон Фика
для
изотропной
среды:
В многомерном случае:
В случае дисперсии с потоком:
вставляем в уравнение неразрывности
в общем случае:

19.

Полный дифференциал функции нескольких переменных
(х+dx,t+dt)- (х,t)=adx+bdt
x+dx, t dt x, t x+dx, t dt x+dx, t x+dx, t x, t
x, t
x+dx, t x, t
[ x dx
x
x dx, t
x+dx, t dt x+dx, t
[ x dx dt
dt
x dx, t
x, t
[ x dx
[ x dx
dt
x
x, t
x, t
x, t
x, t
[
dx
dt
[
dx
[
dt
[t dx dxdt
x
t
x
x
dt
x
t
d
x, t
x, t
[t dx
[ x dt
x
dt
d x, t dx x, t
d
d
[t
[x
v
dt
x
dt
dt
dx
dt
d dx dy d
d
d
vx
vy
dt x dt y dt dt dx
dy
dt
d d
d
d d
d
vx
vy
vz
v grad
dt dx
dy
dz dt
dt

20.

Тензор напряжений вязкого течения
Напряжения рxx,рxy, pxz в направлении х
рyx, рyy, pyz в направлении у
и pzy, pzz, pzx. в направлении z
Тогда на элементарную площадку dsx = dydz
в направлении х на элемент поверхности ds
действует сила dsxpxx + dsypyx+ dszpzx
В общем случае dfk = dsi рik
Для давления Паскаля dfk =-pdsi
Тензор рik
Уравнение Ньютона
dv
V dt dV V dF
pxx
p yx
pzx
pxy pxz
p yy p yz симметричный
pzy pzz
Идеальная жидкость
уравнение Эйлера

21.

Вывод уравнений движения вязкой жидкости Навье-Стокса
Принимая
получим:
и — коэффициенты первой и второй вязкости. Если жидкость несжимаемая, то divv =0
v
v
pik k i
xi xk
Уравнения Навье-Стокса: движения
вязкой жидкости:
Для несжимаемой жидкости:

22.

Уравнение турбулентного движения для природных потоков
Для несжимаемой жидкости система уравнений Рейнольдса в тензорном виде
Упрощения: 1) вертикальные размеры потоков малы по сравнению с горизонтальными
размерами – тогда и ускорения в осреднением движении жидкости вдоль оси z малы по
сравнению с ускорениями вдоль осей х и у; 2) вертикальные размеров потоков малы значит касательные напряжения в жидкости меняются по оси z гораздо сильнее, чем по осям
х, и у; 3) потоки воды в равнинных условиях имеют малые скорости течения - поэтому
турбулентное давление обусловленное пульсациями скоростей в них мало по сравнению с
осредненным гидродинамическим давлением; 4) молекулярные вязкостные напряжения
малы по сравнению с турбулентными напряжениями и могут быть отброшены; 5) для
природных потоков справедливо приближение Буссинеска - линейная связь между
турбулентными напряжениями и градиентами осредненных скоростей – Тогда:

23.

Интегрирование трехмерных уравнений по z с замыкающим уравнением
неразрывности дает систему уравнений планового движения воды в речном русле:
I x i0
z '
z '
, Iy
x
y
Уравнение Сен-Венана
Интегрирование уравнений поверхностного стока на водосборе
Уравнение кинематической волны
z' (х, у, t) - свободная поверхность воды
z0= (х, у) - поверхность водосбора
- =h - глубина потока
qx , qy - расходы воды по направлениям
Сx, Сy - коэффициенты Шези
R - интенсивность осадков
I - инфильтрация воды в почву

24.

В гидрологии уравнение Сен-Венана в виде
F - площадь живого сечения, q - функция
источника (боковой приток в единицу
времени на единицу длины водотока),
uq- относительная скорость бокового
притока, if - уклон трения по формуле
Шези, i0 - уклон дна, положительный в
сторону уменьшения отметок дна
водотока

25.

3.1. ПОВЕРХНОСТНЫЙ ДОЖДЕВОЙ СКЛОНОВЫЙ СТОК
h i ( x ) 5 3
h R I
t x n( x )
x - пространственная координата вдоль поверхности склона;
h = h(x, t) - глубина потока воды на поверхности почвы;
i(x) - уклон поверхности склона; n(x) – коэф-т шероховатости
Шези- Маннинга; R(t) - интенсивность осадков;
I(t) - интенсивность инфильтрации; t - время.
Начальные условия: h( x , t ) 0; x 0, 0 t t S
т.е. в период от t > 0 до t < tS, слой воды на поверхности почвы отсутствует.
Граничные условия: h( 0, t ) 0; x 0, 0 t t
Q
ХИМИЧЕСКИЙ СОСТАВ ПОВЕРХНОСТНОГО СТОКА
C
S hs C s
S
s s
t
t h t
t
1
C Q C R
I
KF 0
hD
C
C
C
C C a1 C C10 a2CT
R
h x
x h x h
h
h
C s
S
h
s Cs C
t
t hs
S
C Kd C
t
C, CS - концентрация в потоке и в растворе зоны эффективного взаимодействия (мг/л);
D– коэф-т дисперсии; S - концентрация сорбированного вещества в почве (мг/г); R, I – интенсивность
атмосферных осадков и инфильтрации в почву (мм/мин); CR – концентрация атмосферных осадков (мг/л
h - глубина потока и hs - "эффективная глубина взаимодействия";
и s - масса доступной почвы на единицу объема поверхностного и внутрипочвенного потоков (г/м3 );
– коэф-т обмена между потоком и зоной взаимодействия (1/с); и Kd – параметры сорбции-десорбции
F - площадь поверхности растворяющегося твердого вещества (соли); K =D/ - коэф-т растворения сол
– толщина переходного слоя, C0- - концентрации насыщения соли у твердой поверхности

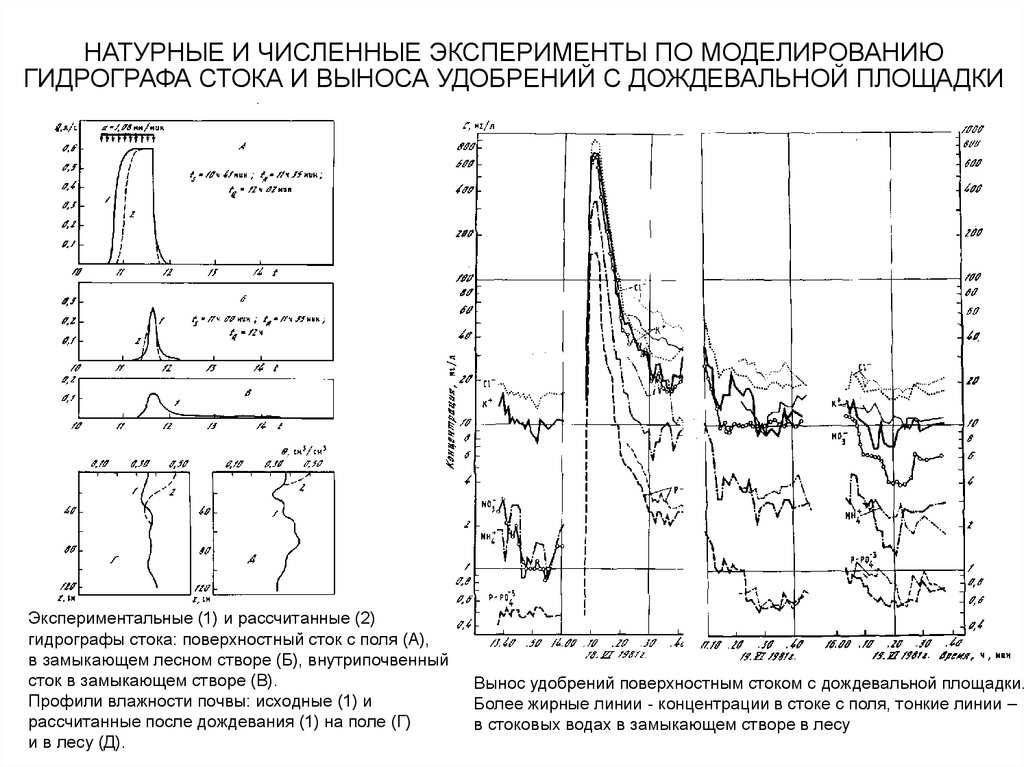
26. НАТУРНЫЕ И ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ПО МОДЕЛИРОВАНИЮ ГИДРОГРАФА СТОКА И ВЫНОСА УДОБРЕНИЙ С ДОЖДЕВАЛЬНОЙ ПЛОЩАДКИ

Экспериментальные (1) и рассчитанные (2)
гидрографы стока: поверхностный сток с поля (А),
в замыкающем лесном створе (Б), внутрипочвенный
сток в замыкающем створе (В).
Профили влажности почвы: исходные (1) и
рассчитанные после дождевания (1) на поле (Г)
и в лесу (Д).
Вынос удобрений поверхностным стоком с дождевальной площадки.
Более жирные линии - концентрации в стоке с поля, тонкие линии –
в стоковых водах в замыкающем створе в лесу

27.

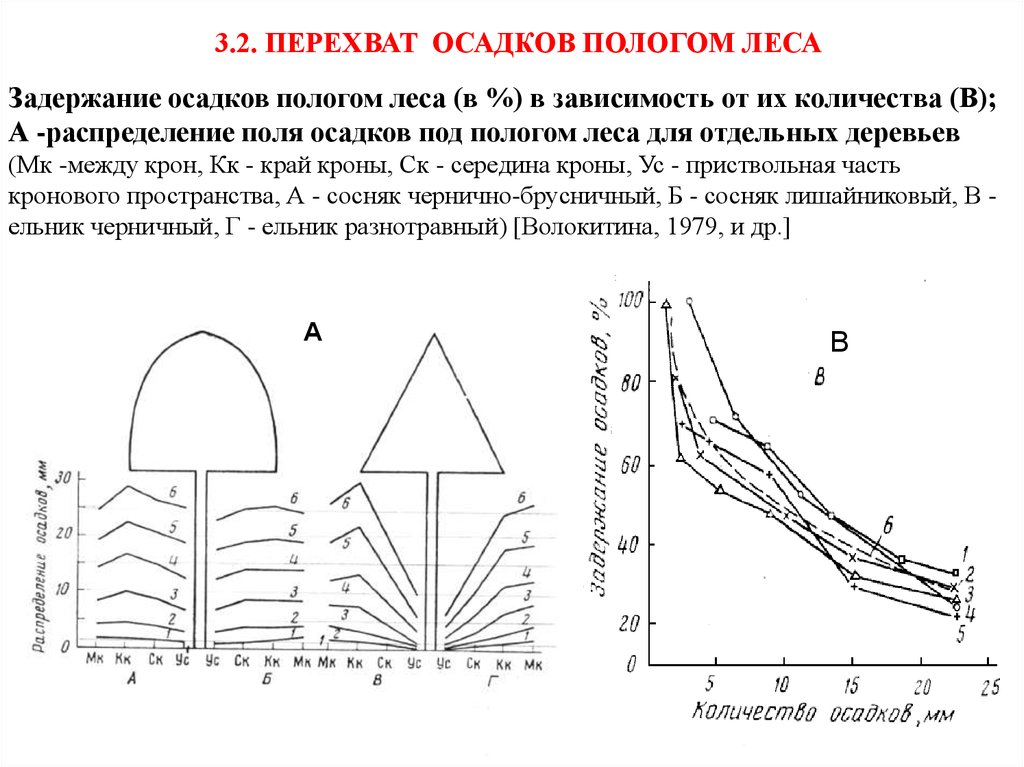
3.2. ПЕРЕХВАТ ОСАДКОВ ПОЛОГОМ ЛЕСА
Задержание осадков пологом леса (в %) в зависимость от их количества (В);
А -распределение поля осадков под пологом леса для отдельных деревьев
(Мк -между крон, Кк - край кроны, Ск - середина кроны, Ус - приствольная часть
кронового пространства, А - сосняк чернично-брусничный, Б - сосняк лишайниковый, В ельник черничный, Г - ельник разнотравный) [Волокитина, 1979, и др.]
А
В

28.

МОДЕЛИРОВАНИЕ ПЕРЕХВАТА ДОЖДЕВЫХ ОСАДКОВ ПОЛОГОМ ЛЕСА
R( z, t )
R( z, t ) D( z, t )U ( z )G ( z )
z
D( z, t )
R( z, t ) D( z, t ) G( z) a( z) 1 D( z, t ) E ( z, t ) a( z)
0
t
С граничным условием
R(0,t) = R0(t) ,
и начальным условием
D(z,0) = D0(z)
,
R(z,t)- интенсивность осадков, см/мин;
Е0 (z,t) - испарение с увлажненной поверхности фитоэлементов (испаряемость), см/мин;
U(z) – площадь поверхности фитоэлементов в единице объема полога на высоте z, 1/см;
G(z) – проекция площади фитоэлементов на единицу поверхности горизонтального
сечения на высоте z;
D(z,t) – безразмерная доля сухих листьев и ветвей в момент t на уровне z;.
(z)- средняя сорбируемость воды на единицу площади фитоэлемента.
z=0 на вершине полога леса, положительна вниз, z=Н – нижняя граница полога
ТРАНСФОРМАЦИЯ ХИМИЧЕСКОГО СОСТАВА ОСАДКОВ ПОЛОГОМ ЛЕСА
C (CR) S
DUK (C0e kRt ) C (1 D)UE0
t
z
t
S
f (C , S )
t
С(z,t) – концентрация компонента в атмосферных осадках, мг/см3 ;
S(z,t) - концентрация компонентов на поверхности клеток фитоэлементов в единице объем
полога леса, мг/см3 ; С0 (z) – начальная концентрация солей и аэрозолей на поверхности
фитоэлементов в единице объема полога, мг/см3 ; k – эмпирический коэффициент; К(z) коэффициент скорости растворения солей, см/мин

29. Интенсивность осадков R и намокаемость фитомассы D по высоте полога леса во времени (R0 - над пологом, D = 1 сухие кроны, ZH -

низ полога)
Интерфейс расчета проникновения
дождевых осадков под крону ели
с учетом разбрызгивания

30.

3.3. ВЕРТИКАЛЬНОЕ ДВИЖЕНИЕ ВЛАГИ В ПОЧВЕ :
DW ( ) K ( ) S ( z, t )
t z
z
вз
K ( ) K f
пв
вз
DW ( ) K ( )
= (z, t) - объемная влажность почвы; z - положительно вниз; t - время;
S(х, t) - расход влаги корнями растений на единицу объема почвы;
К( ) - коэффициент гидравлической проводимости почвы:
3,5
0,25
вз
( ) PB
пв
вз
‚
S ( z, t ) r1 ( z ) E0 ln å‚
ПВ ( 0, t )
E( t ) r2 d ( t ) exp
ПВ
Кf - коэффициент фильтрации в вертикальном направлении;
ВЗ влажность, соответствующая прочно- и рыхлосвязанной воде (ВЗ); ПВ - влажность насыщения (ПВ);
DW( ) - коэффициент диффузии влаги:
РB - капиллярно-сорбционный потенциал насыщения почвы с защемленным воздухом.
(z) - концентрация корней
E(t) – испарение с поверхности почвы; d(t) - дефицит влажности воздуха,
r1 ,r2- эмпирические коэффициенты.
.
Начальные условия:
( z ,0 ) н ( z )
Граничные условия
R( t ) E ( t ) K ( ) 1
z
z 0
ВЕРТИКАЛЬНЫЙ МАССОПЕРЕНОС В ПОЧВАХ
C
mCm imCim f Sm 1 f Sim m D m qCm
t
t
t
t
x
x x
1 f Sim imC im Cm Cim
t
t
S KC N
С - концентрация подвижного растворенного компонента, мг/л;
S- концентрация адсорбированного компонента, мг/г;
D - коэффициент гидродинамической дисперсии;
v - скорость течения воды в порах; - объемное содержание воды в порах;
- объемный вес пористой среды; t - время; z - расстояние;
- коэффициент массопереноса в 1/день; K, N - коэффициенты изотермы сорбци
Индексы m, im -обозначение мобильной и иммобильной зон.
Для почвенной колонки мощностью L граничные условия:
qCo qC m
C
D m ; z 0 , t 0,
m
m
z
С m
0, z L, t 0.
z
начальные условия:
C m ( z,0) C н ( z ); z 0; t 0
C im ( z,0) C1 ( z ); z 0; t 0.

31. НАТУРНЫЕ НАБЛЮДЕНИЯ И ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ПО ВЛАГО- И МАССОПЕРЕНОСУ В ДЕРНОВО-ПОДЗОЛИСТЫХ ПОЧВАХ

НАТУРНЫЕ НАБЛЮДЕНИЯ И ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ПО ВЛАГОИ МАССОПЕРЕНОСУ В ДЕРНОВО-ПОДЗОЛИСТЫХ ПОЧВАХ
Интенсивность фильтрации растворов и промывных вод
в экспериментах на монолитах дерново-подзолистых почв.
А - намытая среднесуглинистая, монолит 3;
Б - среднесуглинистая на покровных суглинках, монолит 4;
1 - температура воды; 2 - подача раствора удобрений;
3 - расходы фильтрата, л/ч.
Ход осадков (а), рассчитанные интенсивности
транспирации (б) и испарения (в), а также профили
влажности почв 12 июня (г), 22 июня (д) и
измеренная концентрация корней (е). 1 рассчитанные профили; 2 - измеренные профили
влажности почв
Экспериментальные данные (точки) и рассчитанные в
численном эксперименте выходные кривые для
дерново-подзолистой среднесуглинистой почвы
под ельником-кисличником

32.

3.4. ГРУНТОВЫЙ И ПОДЗЕМНЫЙ СТОК В ГЕОСИСТЕМАХ
К ВЫВОДУ ЗАКОНА ДАРСИ
Равновесие элементарного столбика жидкости
P1= p1 ,
P1–P2+G sin = или
P2= p2 ,
p1 -p2 + g l sin = , Так как
G = g l
l sin =z1-z2
p1 -p2 + g (z1-z2) = .
H =p/ g+z – пьезометрический (гидростатический) напор
Q=-k (H2-H1)/ l=-k ( H/ l)
совершая предельный переход:

33.

Движение грунтовых вод над горизонтальным водоупором
при отсутствии фильтрационного питания
Граничные условия:
H=h1 при x=x1;
H=h2 при x=x2;
разделим переменные и проинтегрируем
дифференциальное уравнение Дарси с
учетом пределов изменения переменных
величин h и х:
Кривая депрессии потока грунтовых вод:

34.

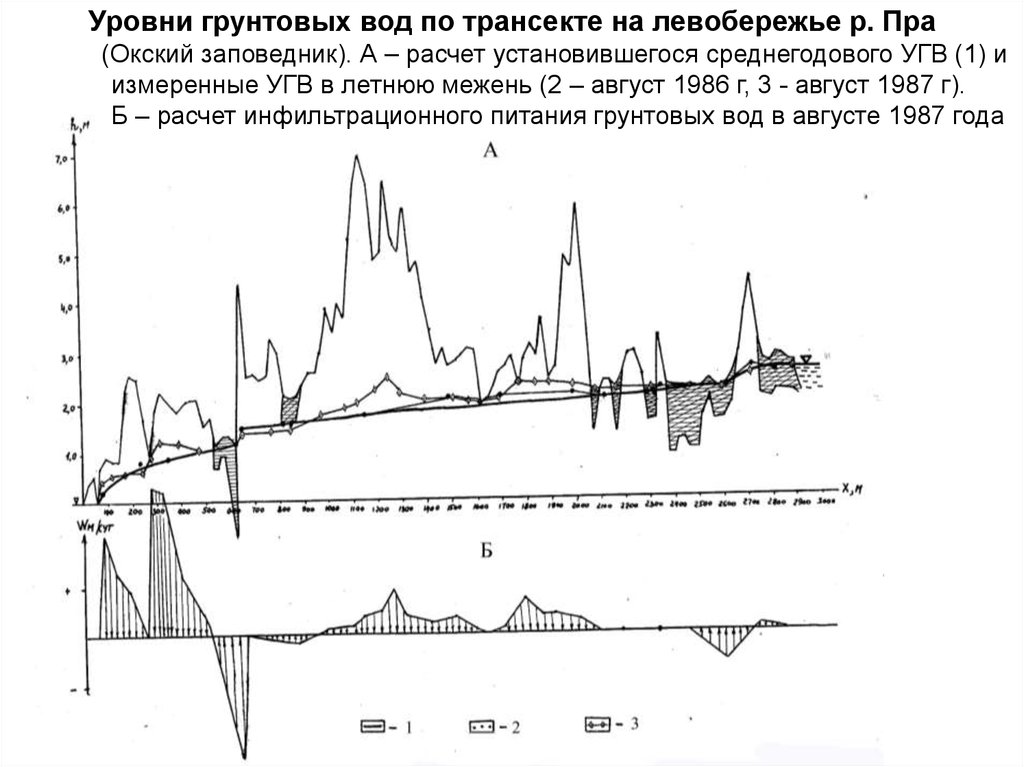
Уровни грунтовых вод по трансекте на левобережье р. Пра
(Окский заповедник). А – расчет установившегося среднегодового УГВ (1) и
измеренные УГВ в летнюю межень (2 – август 1986 г, 3 - август 1987 г).
Б – расчет инфильтрационного питания грунтовых вод в августе 1987 года

35.

36.

Теплоперенос в различных средах
Если T= Т(х, t) - температура тела в точке х в момент t, тогда плотность
тепловой энергии Q можно записать
Q = с 0 Т
0 - массовая линейная плотность тела, с - коэффициент теплоемкости
кал/(г·град) при небольших изменениях Т можно принять постоянным.
Чтобы получить из общего уравнения переноса уравнение переноса теплоты,
вводим потенциал переноса в виде = С Т.
Согласно градиентному закону Фурье:
qQ T x
(1)
- коэффициент теплопроводности, кал/(см °С·сут) или Дж/(с∙м∙0С) = Вт/(м·К),
можно считать постоянным. Подставляя (1) в уравнение неразрывности для
тепловой энергии:
(2)
вынося и с 0 за скобки и обозначая kT= /c 0 коэффициент температуро2
проводности, получаем уравнение теплопроводности:
T
T
kT 2
t
x (3)
В общем виде уравнение
(2) переноса теплоты

37.

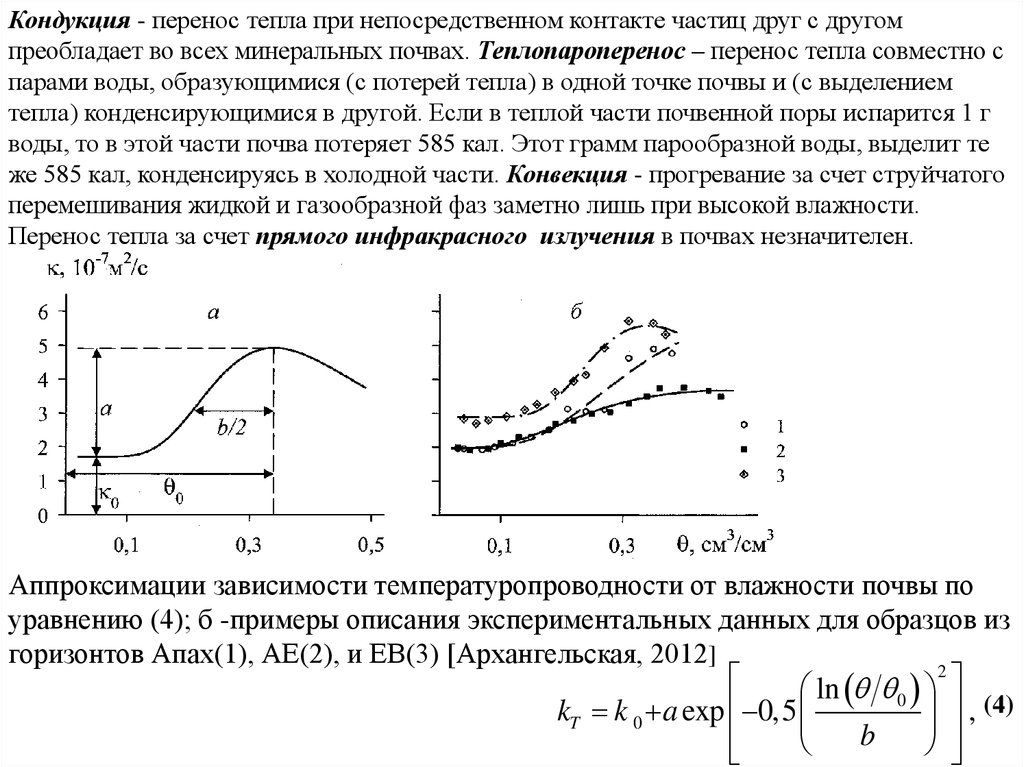
Кондукция - перенос тепла при непосредственном контакте частиц друг с другом
преобладает во всех минеральных почвах. Теплопароперенос – перенос тепла совместно с
парами воды, образующимися (с потерей тепла) в одной точке почвы и (с выделением
тепла) конденсирующимися в другой. Если в теплой части почвенной поры испарится 1 г
воды, то в этой части почва потеряет 585 кал. Этот грамм парообразной воды, выделит те
же 585 кал, конденсируясь в холодной части. Конвекция - прогревание за счет струйчатого
перемешивания жидкой и газообразной фаз заметно лишь при высокой влажности.
Перенос тепла за счет прямого инфракрасного излучения в почвах незначителен.
Аппроксимации зависимости температуропроводности от влажности почвы по
уравнению (4); б -примеры описания экспериментальных данных для образцов из
горизонтов Апах(1), АЕ(2), и ЕВ(3) [Архангельская, 2012]
2
ln 0
kT k 0 a exp 0,5
b
, (4)

38.

Распределения температуры при наличии фазового перехода и
движения раздела фаз
Условие на границе промерзания воды
при t 0 условие на
границе раздела фаз
с дополнительными условиями:
граничное условие:
начальное условие:
С условиями на границе промерзания воды:
Условие в почве с содержанием воды:
Совместный эффект влияния на тепло- и влагоперенос термических и влажностных
градиентов в почвах:

39.

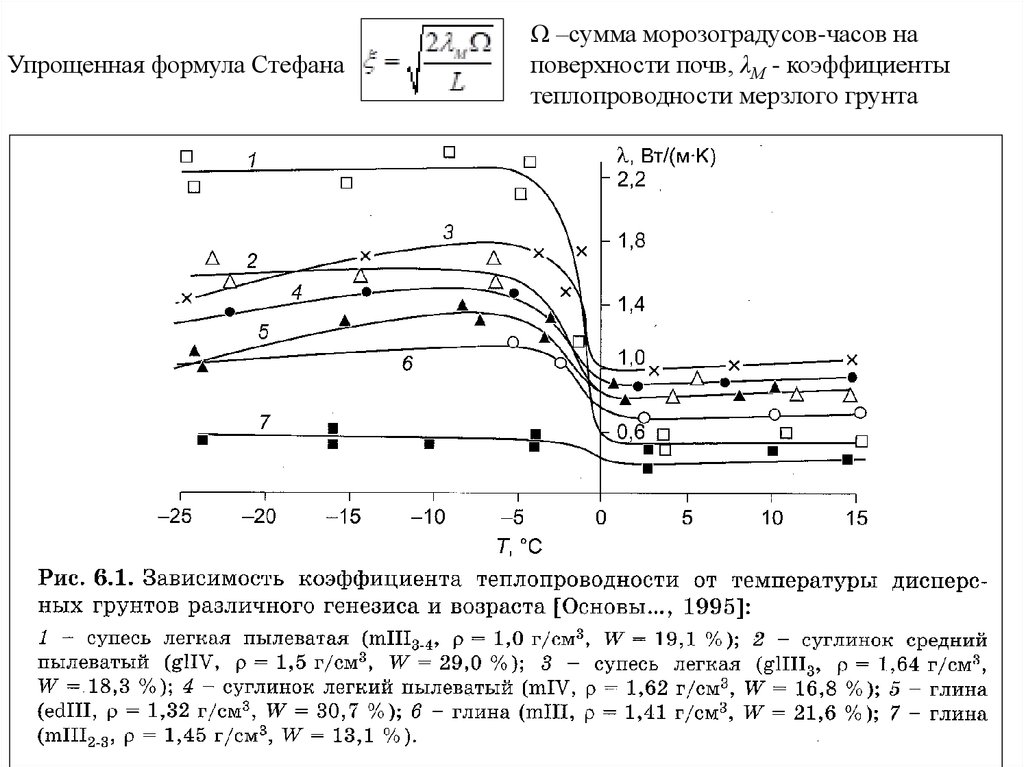
Упрощенная формула Стефана
Ω –сумма морозоградусов-часов на
поверхности почв, λМ - коэффициенты
теплопроводности мерзлого грунта

40.

Гидрологическое функционирование и структура болотных
ландшафтов
Схема роста простого выпуклого симметричного болотного массива

41.

42.

43.

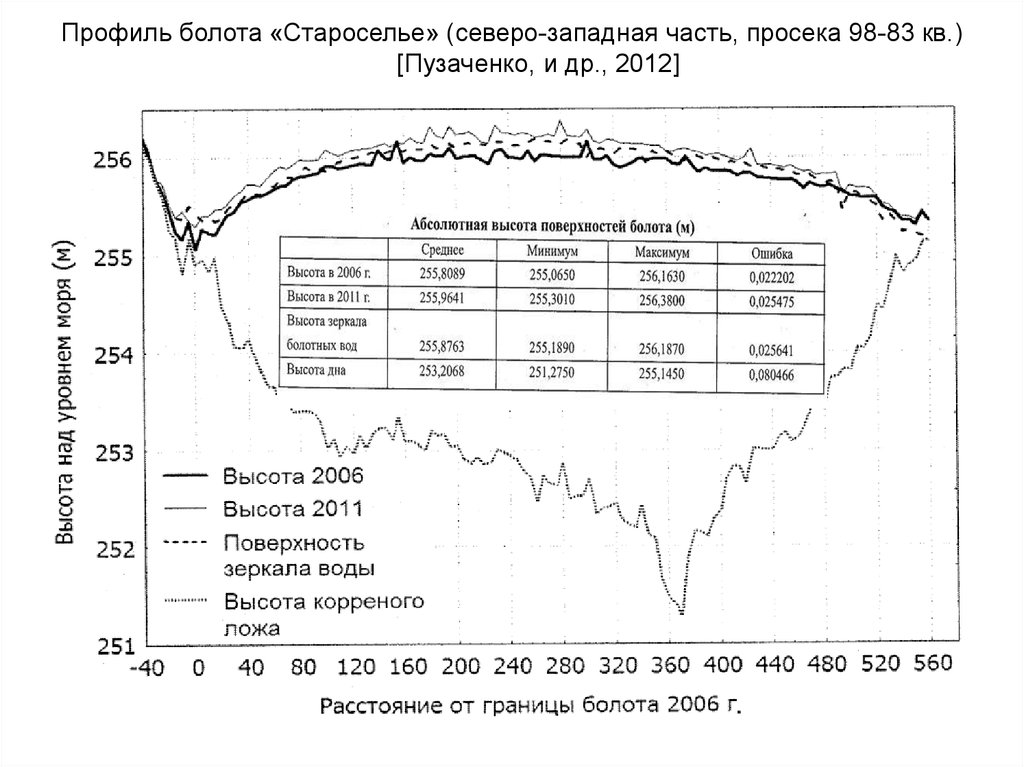
Профиль болота «Староселье» (северо-западная часть, просека 98-83 кв.)
[Пузаченко, и др., 2012]

44.

Фильтрационные характеристики болотной фации
q k grad h
В простом одномерном случае:
q k0 ( z0 z )i
у - расстояние
по вертикали от начала координат до уровня грунтовых вод , y1 - до
поверхности болота; z - уровень грунтовых вод от поверхности массива: z =f(r, у, ); zо
толщина деятельного горизонта: z0 = (r, у, );
w f
Р - интенсивность прихода влаги на единицу площади болота:
p
t
w и f - соответственно объемы осадков и испарения за время t.
Уклон поверхности болотного массива i ;
Коэффициент фильтрации kz в деятельном горизонте, k0 – средний в слое (zo-z),
kмакс - коэффициент фильтрации при z=0 (т. е. у поверхности болота)
Проточность qz (горизонтальный фильтрационный расход через вертикальное
поперечное сечение высотой (zo—z) и шириной, равной единице)
Модуль горизонтальной проточности Mz.
z
z0
kz dz
k z kмакс
z0
z 1
kì àêñ
dz
k0
z0 z z0 z z z 1 m
z
m
0
,
qz i k z dz
z
qz i z0 z k0
z
qz 0
M z k z dz
i
z

45.

Коэффициент фильтрации kz=f(z) в деятельном горизонте разных болотных фаций
[Иванов, 1984]. 1 - осоково-гипновый; 2 - вейниково-березовый; 3 - сосново-сфагново-кустарничковый,
элемент микрорельефа - повышение; 4 - комплекс группы фаций ленточногрядовой структуры, элемент
микрорельефа - гряда сфагново-кустарничково-сосновая; 5 - то же, элемент микрорельефа - гряда
сфагново-кустарничковая, облесенная сосной; 6 - сфагново-кустарничковый, облесенный сосной, элемент
микрорельефа - повышение

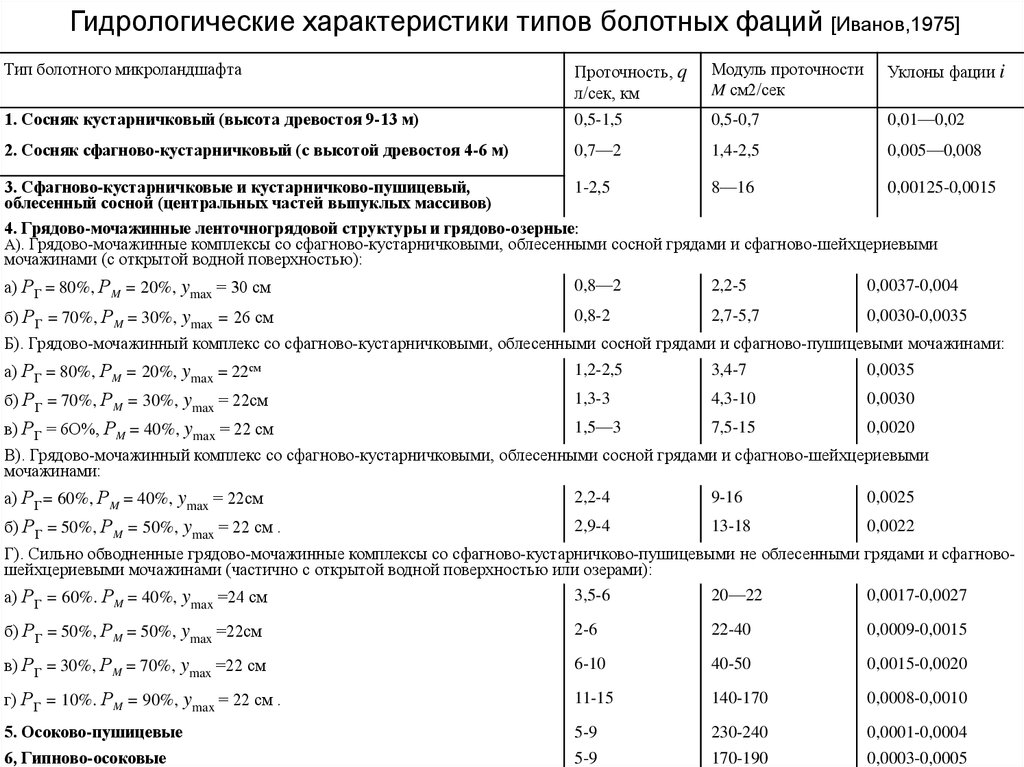
46.

Гидрологические характеристики типов болотных фаций [Иванов,1975]
Тип болотного микроландшафта
Проточность, q
л/сек, км
Модуль проточности
M см2/сек
Уклоны фации i
1. Сосняк кустарничковый (высота древостоя 9-13 м)
0,5-1,5
0,5-0,7
0,01—0,02
2. Сосняк сфагново-кустарничковый (с высотой древостоя 4-6 м)
0,7—2
1,4-2,5
0,005—0,008
3. Сфагново-кустарничковые и кустарничково-пушицевый,
облесенный сосной (центральных частей выпуклых массивов)
1-2,5
8—16
0,00125-0,0015
4. Грядово-мочажинные ленточногрядовой структуры и грядово-озерные:
А). Грядово-мочажинные комплексы со сфагново-кустарничковыми, облесенными сосной грядами и сфагново-шейхцериевыми
мочажинами (с открытой водной поверхностью):
а) РГ = 80%, РM = 20%, ymax = 30 см
0,8—2
2,2-5
0,0037-0,004
б) РГ = 70%, РM = 30%, ymax = 26 см
0,8-2
2,7-5,7
0,0030-0,0035
Б). Грядово-мочажинный комплекс со сфагново-кустарничковыми, облесенными сосной грядами и сфагново-пушицевыми мочажинами:
а) РГ = 80%, РM = 20%, ymax = 22см
1,2-2,5
3,4-7
0,0035
б) РГ = 70%, РM = 30%, ymax = 22см
1,3-3
4,3-10
0,0030
в) РГ = 6О%, РM = 40%, ymax = 22 см
1,5—3
7,5-15
0,0020
В). Грядово-мочажинный комплекс со сфагново-кустарничковыми, облесенными сосной грядами и сфагново-шейхцериевыми
мочажинами:
а) РГ= 60%, РM = 40%, ymax = 22см
2,2-4
9-16
0,0025
б) РГ = 50%, РM = 50%, ymax = 22 см .
2,9-4
13-18
0,0022
Г). Сильно обводненные грядово-мочажинные комплексы со сфагново-кустарничково-пушицевыми не облесенными грядами и сфагновошейхцериевыми мочажинами (частично с открытой водной поверхностью или озерами):
а) РГ = 60%. РM = 40%, ymax =24 см
3,5-6
20—22
0,0017-0,0027
б) РГ = 50%, РM = 50%, ymax =22см
2-6
22-40
0,0009-0,0015
в) РГ = 30%, РM = 70%, ymax =22 см
6-10
40-50
0,0015-0,0020
г) РГ = 10%. РM = 90%, ymax = 22 см .
11-15
140-170
0,0008-0,0010
5. Осоково-пушицевые
5-9
230-240
0,0001-0,0004
6, Гипново-осоковые
5-9
170-190
0,0003-0,0005

47.

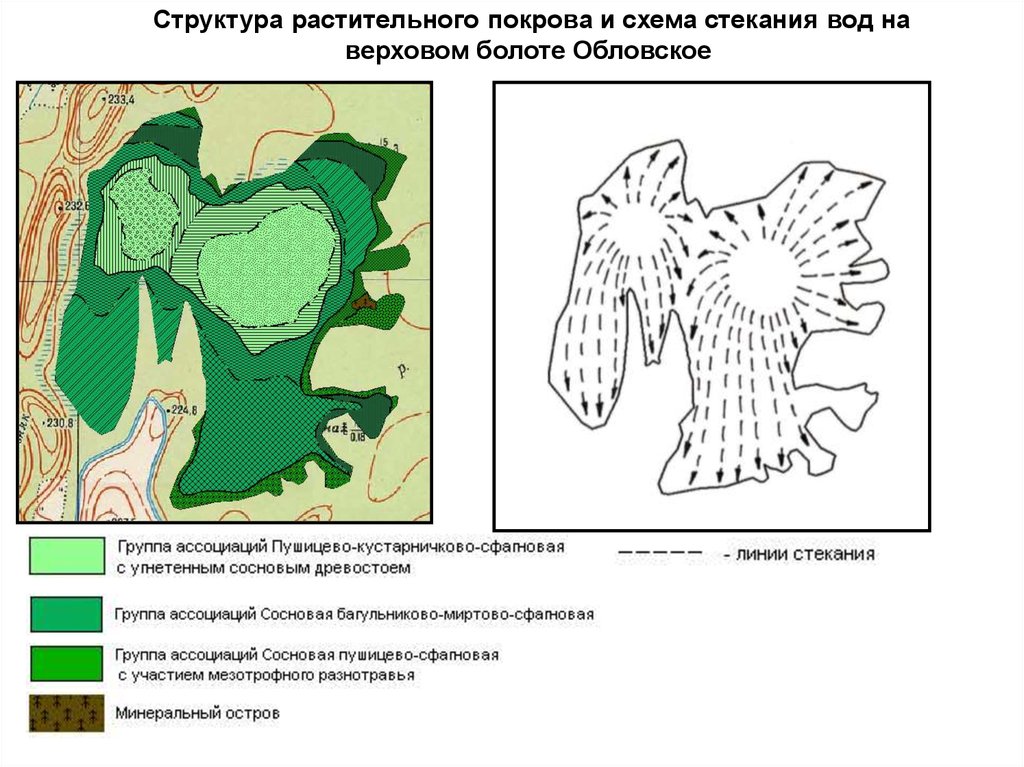
48.

Структура растительного покрова и схема стекания вод на
верховом болоте Обловское

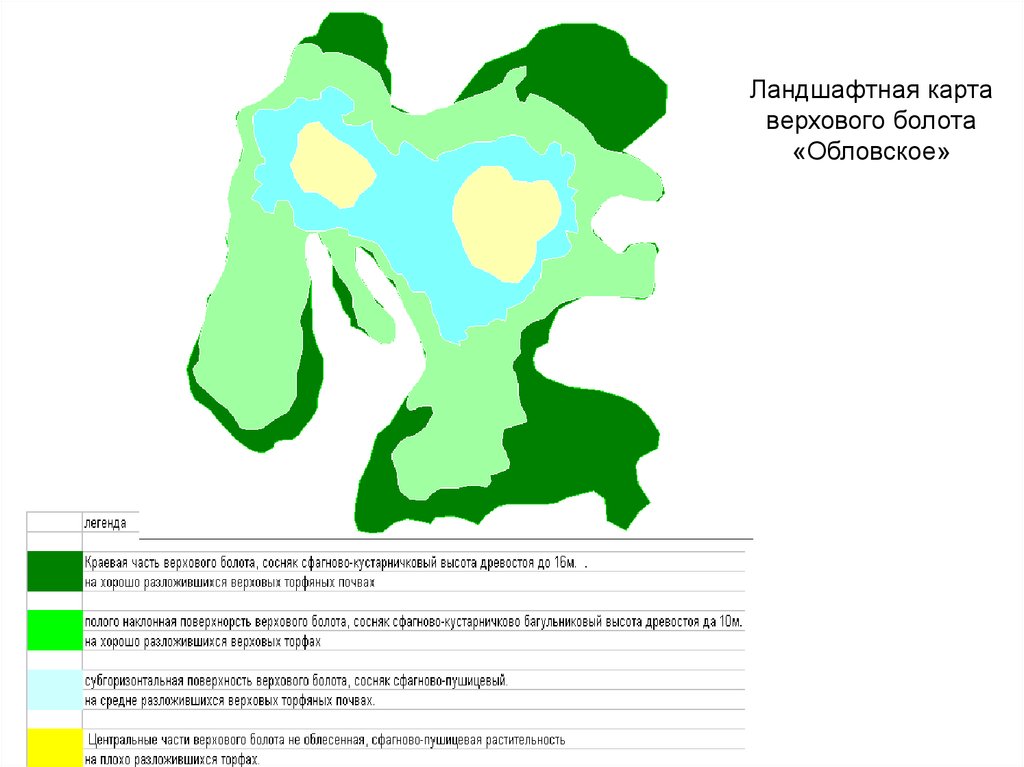
49.

Ландшафтная карта
верхового болота
«Обловское»

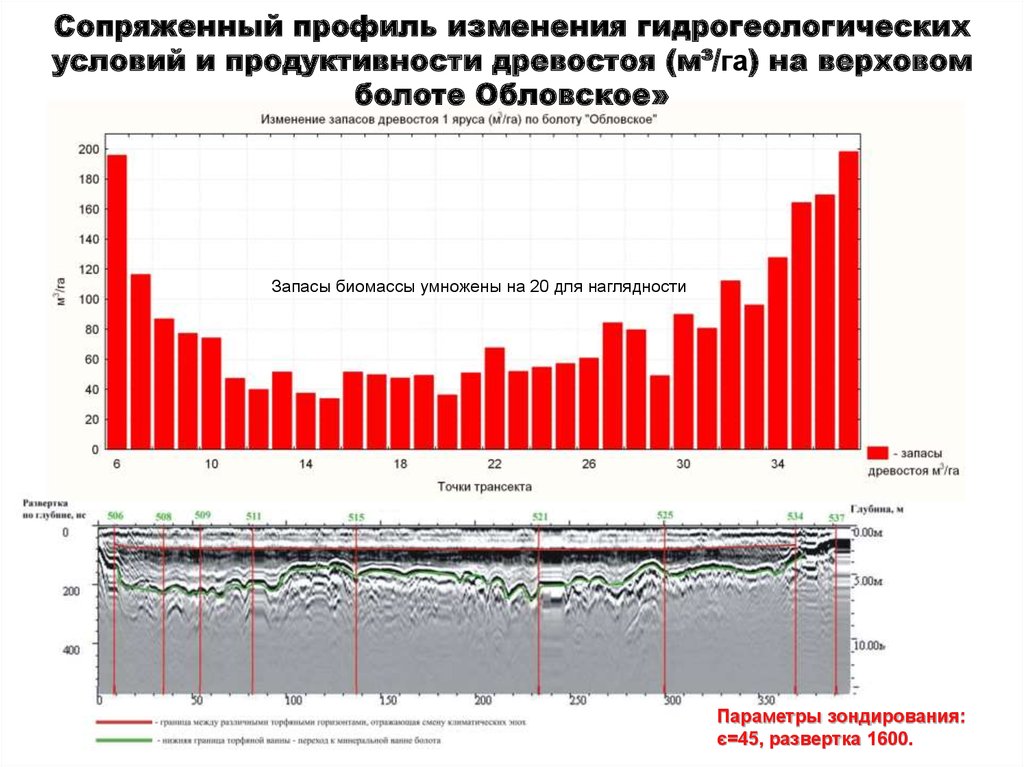
50.

Сопряженный профиль изменения гидрогеологических
условий и продуктивности древостоя (м³/га) на верховом
болоте Обловское»
Запасы биомассы умножены на 20 для наглядности
Параметры зондирования:
є=45, развертка 1600.

51. Пространственный анализ гидроморфологических связей в болотном массиве.

Разрез болотного массива вдоль линии cтока.
1- поверхность болота, 2 - уровень грунтовых вод,
3 - граница деятельного горизонта и торфяная залежь,
4 - дно болота и подстилающий минеральный грунт.
s - расстояния вдоль линии стока; bs - длина дуги
горизонтали на расстоянии s; b0—длина дуги
горизонтали в начале участка; q0 - единичный
расход в деятельном горизонте в начале участка;
qs - единичный расход на расстоянии s;
Тип ПТК характеризуется: средним модулем
проточности Ms, формой потока в плане - b0, bS ,.и
внешним (q0) и внутренним ( pS) питанием.
Гидродинамический профиль
s1
qsbs q0b0 psbs ds ,
0
qs
s1
q0b0 psbs ds
0
bs
qs M si
i =dy/ds
При наличии водораздельных точек (линий), для которых s=0 и внешнее питание q0 =0 и
соответственно i=0 уравнение гидродинамического профиля упрощаем:
Интегрирование уравнения при ряде упрощающих
предположений дает выражение:
n – характеризует сходимость-расходимость линий тока,
на симметричном круглом болоте растекание от водораздела внутри массива, при n=1 и замене s на r (линии
тока совпадают с радиусами) дает [Иванов, 1975 ]:

52.

Нормальный профиль выпуклых болотных массивов верхового типа
В соответствии с уравнением Дарси
pr
q
z0 zq k0i Mi
2
q kh grad h
mr
dy
M
2
dr
m 2 2
r0 r
► ymax y
4M
ymax - превышение высшей точки массива над его окраинами; rо - радиус болотного массива
Если ω - площадь данного болотного массива то r0 = rn
rn
,
Нормальные профили болот при М = 2,5 и 20 см2/сек. и максимальных
выпуклостях уmax= 2, 4 и 6 м.

53.

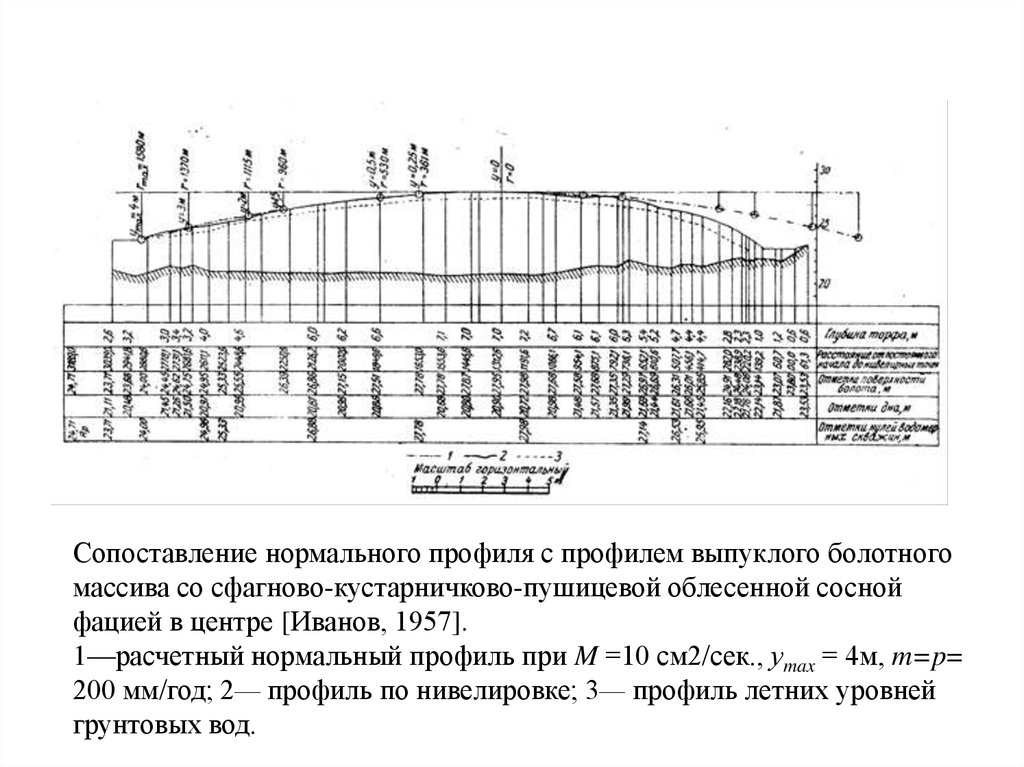
Сопоставление нормального профиля с профилем выпуклого болотного
массива со сфагново-кустарничково-пушицевой облесенной сосной
фацией в центре [Иванов, 1957].
1—расчетный нормальный профиль при M =10 см2/сек., уmax = 4м, m=p=
200 мм/год; 2— профиль по нивелировке; 3— профиль летних уровней
грунтовых вод.

54.

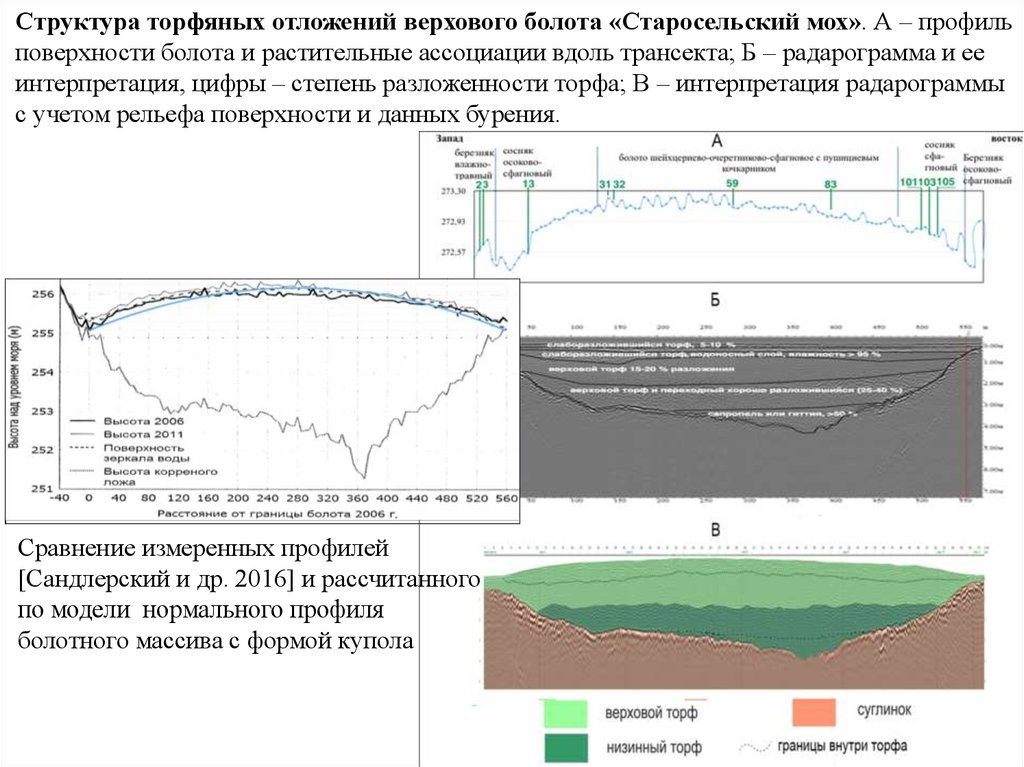
Структура торфяных отложений верхового болота «Старосельский мох». А – профиль
поверхности болота и растительные ассоциации вдоль трансекта; Б – радарограмма и ее
интерпретация, цифры – степень разложенности торфа; В – интерпретация радарограммы
с учетом рельефа поверхности и данных бурения.
Сравнение измеренных профилей
[Сандлерский и др. 2016] и рассчитанного
по модели нормального профиля
болотного массива с формой купола

55.

Вертикальный профиль торфа верхового болота Обловское тр№6
224
223
222
поверхность
220
минеральное дно
219
УГВ
218
217
216
39
37
35
33
31
29
27
25
23
21
19
17
15
13
11
9
7
5
3
215
1
Набс
221

56.

Разделяя переменные проинтегрируем при условии М = const,
но в пределах изменения r от 0 до rn и у от 0 до yтaх получим
уравнение связывает: средний модуль стока (т) с болотного массива, средний
модуль проточности M (сочетание типов болотных фаций, составляющих
болотный массив), средний линейный размер массива r (или его площадь ω) и
величину максимального превышения поверхности над его окраинами ymax.
Массивы верховых сосново-сфагновых ландшафтов объединены в зону олиготрофных и
евтрофных сосново-сфагновых торфяников [Пьявченко, 1985] с границами приблизительно
по изолиниям годовой нормы стока 250 мм на севере и 160 мм на юге ЕТР (до 100мм/год в
Сибири). Большие грядово-мочажинные комплексы реализуются в зоне выпуклых
олиготрофных торфяников с нормой стока 250-300мм/год в ЕТР (до 150мм/год в Сибири).

57.

Математическое моделирование снежных лавин
v - скорость лавины вдоль склона (м/с), mл - масса
лавины (кг); g - ускорение свободного падения (м/с2);
φ - угол склона, градусы; Кg - проекция суммарной
Критическая толщина пласта Hn
силы сопротивления движению лавины (м/с2)
ρс - плотность снега; ∆р – разность давления (р1-р2); С
– сила сцепления;
Система моделирования снежных лавин RAMMS
ρ – плотность потока; H – высота потока; U –
скорость потока; μ - коэффициентом силы сухого
кулоновского трения; ξ – коэффициент силы
турбулентного сопротивления, пропорциональной
квадрату скорости движения снежной массы
Коэффициенты сопротивления для
моделирования лавин в горах Алатау
по модели RAMMS [Благовещенский и
др., 2017]

58.

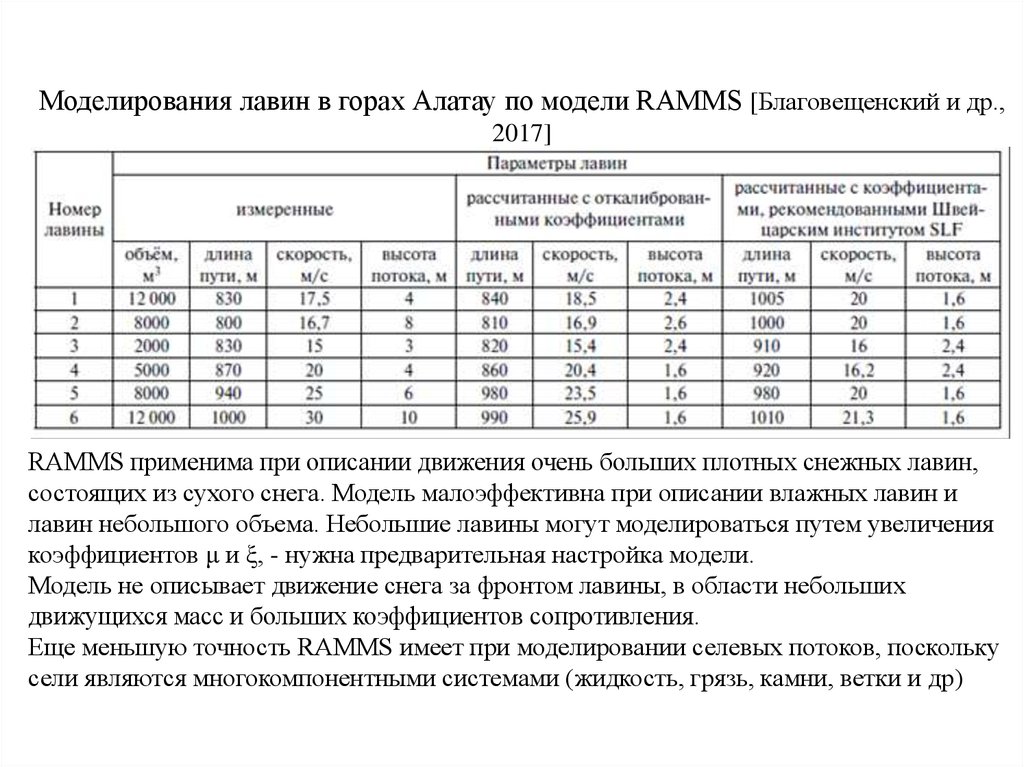
Моделирования лавин в горах Алатау по модели RAMMS [Благовещенский и др.,
2017]
RAMMS применима при описании движения очень больших плотных снежных лавин,
состоящих из сухого снега. Модель малоэффективна при описании влажных лавин и
лавин небольшого объема. Небольшие лавины могут моделироваться путем увеличения
коэффициентов μ и ξ, - нужна предварительная настройка модели.
Модель не описывает движение снега за фронтом лавины, в области небольших
движущихся масс и больших коэффициентов сопротивления.
Еще меньшую точность RAMMS имеет при моделировании селевых потоков, поскольку
сели являются многокомпонентными системами (жидкость, грязь, камни, ветки и др)

59.

Моделирование снежной лавины на основе метода сглаженных частиц
Состояние элемента снега i определяется
X – вдоль склона, Y – вертикальная
декартовыми координатами его центра (xi ,yi)
и двумя составляющими скорости (vxi, vyi);
FУij и FВij – силы упругого и вязкого
взаимодействия элементов снега i и j; NЭ –
общее количество элементов снега в модели.
1) Если элементы i и j не связаны, то
2) Если элементы i и j связаны и слабо взаимодействуют
3) Если элементы i и j связаны и сильно взаимодействуют
FУxij и FУyij – составляющие силы FУij;
cО и cС – жесткости упругого слабого и
сильного взаимодействия элементов,

60.

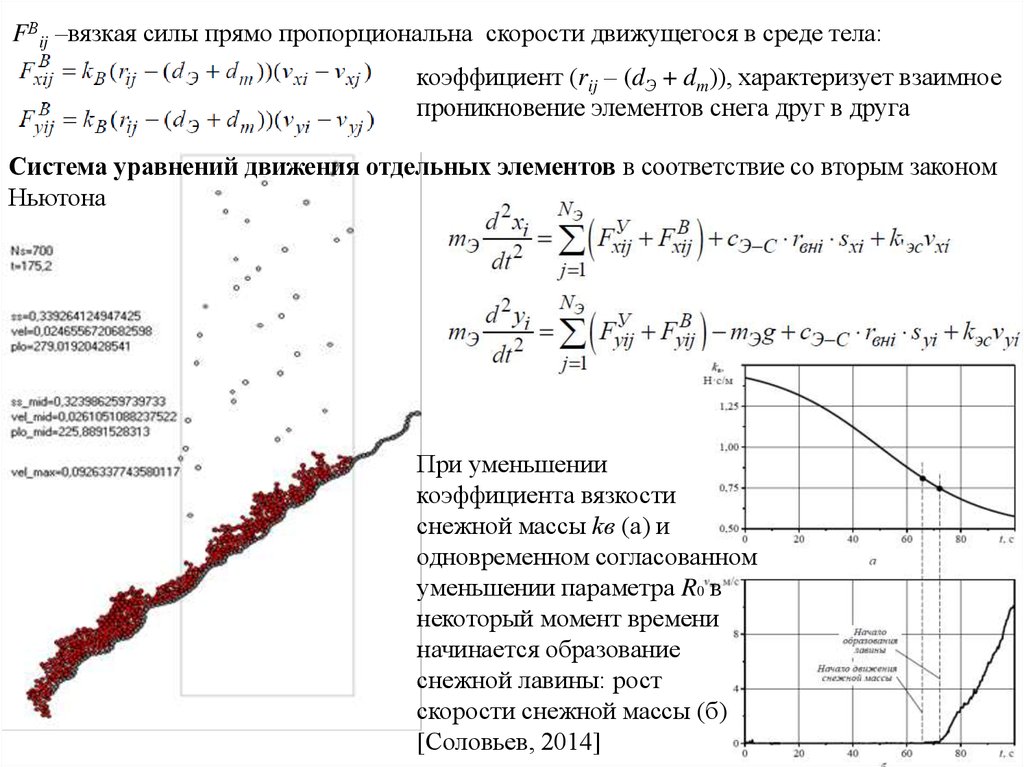
FВij –вязкая силы прямо пропорциональна скорости движущегося в среде тела:
коэффициент (rij – (dЭ + dm)), характеризует взаимное
проникновение элементов снега друг в друга
Система уравнений движения отдельных элементов в соответствие со вторым законом
Ньютона
При уменьшении
коэффициента вязкости
снежной массы kв (а) и
одновременном согласованном
уменьшении параметра R0 в
некоторый момент времени
начинается образование
снежной лавины: рост
скорости снежной массы (б)
[Соловьев, 2014]

61.

Траектории движения снежных фрагментов по
склону при движении снежной массы. Белые
круги - последовательные положения снежных
элементов [Соловьев, 2014]. На склонах малой
крутизны, снежные фрагменты скользят по
склону или по нижележащим слоям снега.
Скорость скольжения элементов, находящихся в
непосредственном соприкосновении со склоном
минимальна, и чем выше по отношению к склону
расположен фрагмент снега, тем больше его
скорость (φ ≤ 40°). При большой крутизне склона
движение фрагментов снега начинается так же как
скольжение, однако через незначительное время
сменяется "прыжками" (φ = 50°). Фрагменты снега
в лавине находятся в «прыгающем» постоянно
ускоряющемся движении фрагментов с
интервалом 0,5 с
Верификация модели
Распределения давления по
высоте снежной массы h (а), и
влияние угла склона α на длину
пробега лавины L(б) [Соловьев,
2014]

62. Заключение

Единая теоретическая база уравнений математической физики использована
для описание структуры и функционирования геосистем. Наименьшими
материальными объектами (точками), из которых состоят пространственнотерриториальные комплексы, выступают элементы поверхности рельефа
(пиксели ЦМР), имеющие географические координаты, а их состояние
описывается параметрами градиентов геофизических полей.
На логике классических определений ландшафтоведения предложены
алгоритмы выделения однородных по параметрам геосистем. Результаты
моделирования показывают необходимость учитывать роль факторов
дифференциации ПТК в конкретных физико-географических условиях.
Получены достоверные взаимосвязи структуры и функционирования геосистем
низкого иерархического уровня. Морфометрическое описание рельефа и
геофизическая дифференциация ПТК являются адекватными граничными
условиями для физико-математических моделей функционирования геосистем
Проведено дедуктивное построение теории гидроциркуляционного
функционирования геосистем от постулатов до уравнений теоретической
гидромеханики, показаны пути упрощения и использования этих уравнений для
моделирования структурообразующих процессов в геосистемах.
Уникальным примером синтеза ландшафтно-морфологического,
биогеофизического и гидродинамического описания болотных ландшафтов
являются работы К.Е. Иванова, выполненые полвека тому назад.
Таким образом, единый физический подход, основанный на общенаучных
понятиях и терминах уравнений теории поля, имеет важнейшее значение в
плане включения любых частных процессов и систем в более общие
геосистемы, для построения общей теории геосистем.