Похожие презентации:
Основы программирования на языке Python. Логическая операция
1. 13 занятие
Школа::Кода«Основы программирования на языке Python»
2.
Проверка присутствия2
3.
Логическая операция – способ построениясложного
высказывания
из
данных
высказываний,
при
котором
значение
истинности сложного высказывания полностью
определяется значениями истинности исходных
высказываний.
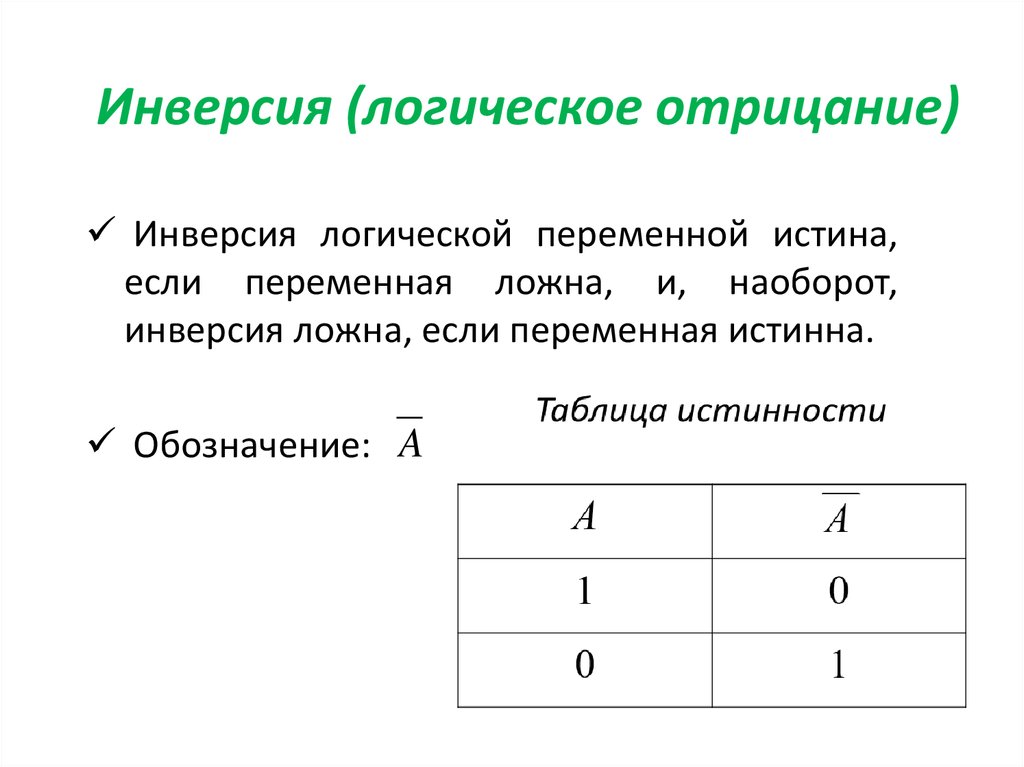
4. Инверсия (логическое отрицание)
Инверсия логической переменной истина,если переменная ложна, и, наоборот,
инверсия ложна, если переменная истинна.
Обозначение: A
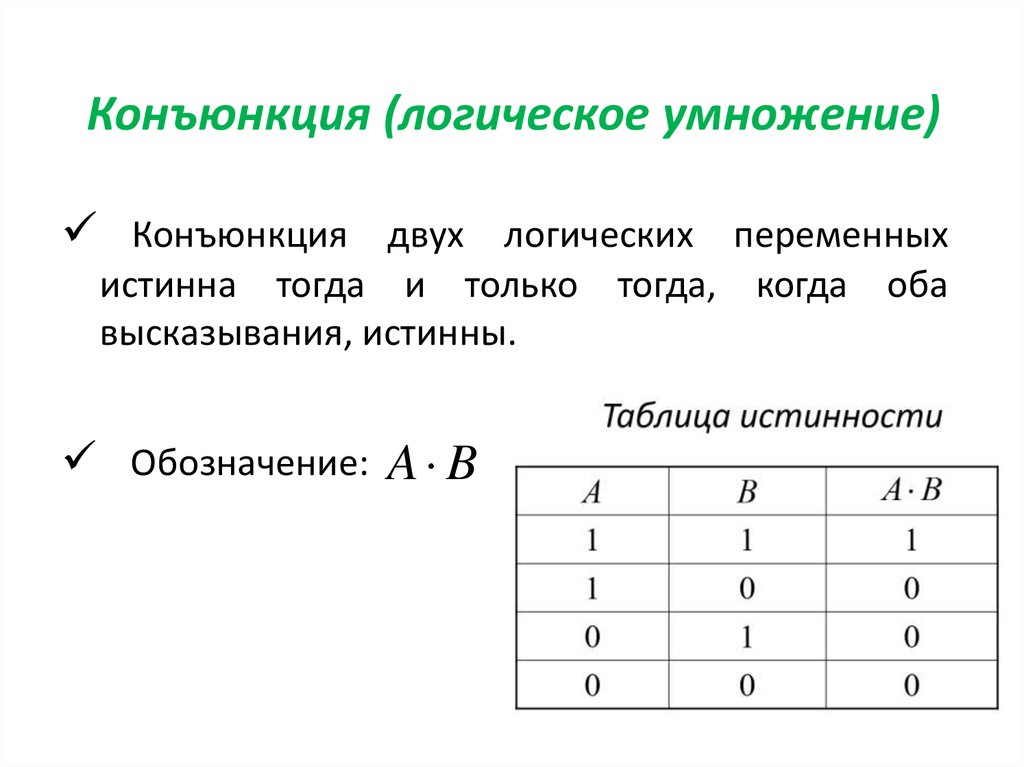
5. Конъюнкция (логическое умножение)
Конъюнкция двух логических переменныхистинна тогда и только тогда, когда оба
высказывания, истинны.
Обозначение: A B
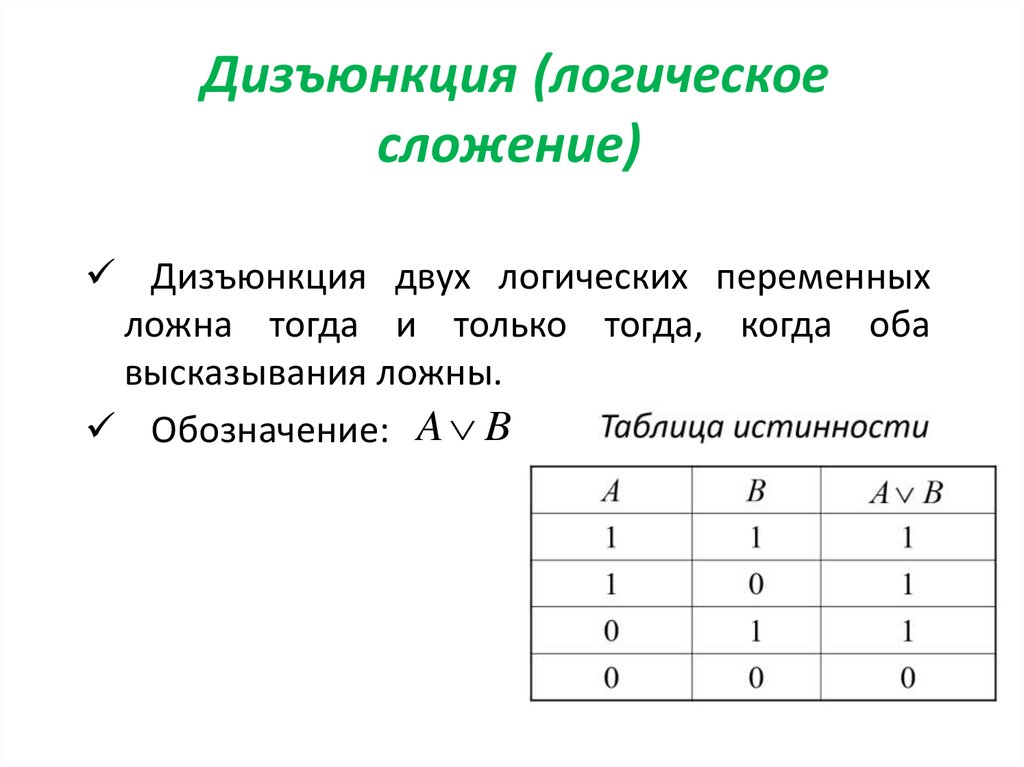
6. Дизъюнкция (логическое сложение)
Дизъюнкция двух логических переменныхложна тогда и только тогда, когда оба
высказывания ложны.
Обозначение: A B
7. Импликация (логическое следование)
Импликация двух логических переменныхложна тогда и только тогда, когда из истинного
основания следует ложное следствие.
Обозначение: A B
А - условие
В - следствие
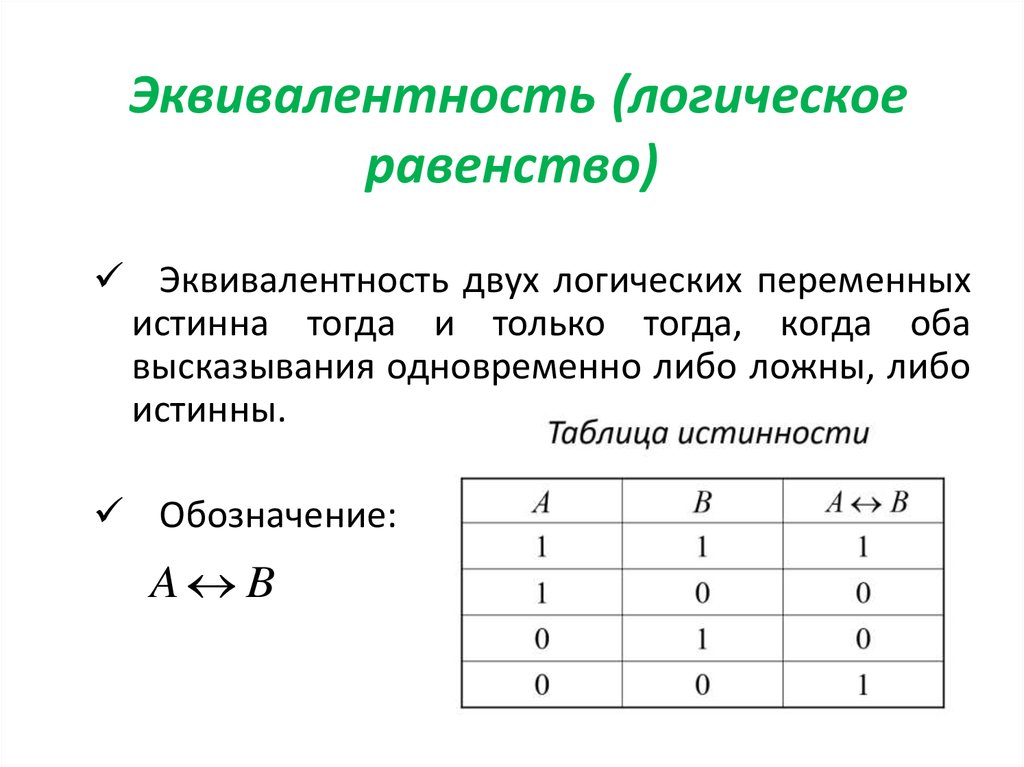
8. Эквивалентность (логическое равенство)
Эквивалентность двух логических переменныхистинна тогда и только тогда, когда оба
высказывания одновременно либо ложны, либо
истинны.
Обозначение:
A B
9. Приоритет выполнения логических операций
При вычислении значения логического выражения(формулы) логические операции вычисляются в
определенном порядке, согласно их приоритету:
1.инверсия,
2.конъюнкция,
3.дизъюнкция,
4.импликация и эквивалентность.
Операции одного приоритета выполняются слева
направо.
Для
изменения
порядка
действий
используются скобки.
10. Пример
Дана формулаA B C D A
Определите порядок вычисления.
Порядок вычисления:
Инверсия – A
Конъюнкция – C D
Дизъюнкция – A B
Импликация – A B C D
Эквивалентность –
A B C D A
11.
Таблица истинности - таблица, показывающая,какие
значения принимает составное высказывание при всех
сочетаниях (наборах) значений входящих в него простых
высказываний.
Логическое выражение - составные высказывания в виде
формулы.
Равносильные логические выражения – логические
выражения, у которых последние столбцы таблиц
истинности совпадают. Для обозначения равносильности
используется знак «=».
11
12.
Алгоритм построения таблицы истинности:1.
подсчитать количество переменных n в логическом
выражении;
2. определить число строк в таблице по формуле m=2n,
где n - количество переменных;
3.
подсчитать количество логических операций в
формуле;
4.
установить последовательность выполнения
логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных +
число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам,
выполняя логические операции в соответствии с
установленной в пункте 4 последовательностью.
12
13.
Заполнение таблицы:1.
разделить колонку значений первой переменной
пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2.
разделить колонку значений второй переменной на
четыре части и заполнить каждую четверть чередующимися
группами «0» и «1», начиная с группы «0»;
3.
продолжать деление колонок значений последующих
переменных на 8, 16 и т.д. частей и заполнение их группами
«0» или «1» до тех пор, пока группы «0» и «1» не будут
состоять из одного символа.
13
14.
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицуистинности.
Количество логических переменных 3,
следовательно, количество строк - 23 = 8.
Количество логических операций в формуле 5, количество
логических переменных 3, следовательно количество
столбцов - 3 + 5 = 8.
14
15.
Пример 2. Определите истинность логическоговыражения F(А, В) = (А\/ В)/\(¬А\/¬В)
Пример 3. Постройте таблицу истинности для логического
выражения F = (A\/ B) /\ ¬С
Пример 4. Определите истинность формулы:
F = ((С \/В) => В) /\ (А /\ В) => В.
15
16.
Пример 5. Символом F обозначено одно из указанныхниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
X Y Z F
0
0
0
1
0
0
1
0
0
1
0
1
Какое выражение соответствует F?
1) ¬X/\¬Y/\Z
2) ¬X\/¬Y\/Z
3) X\/Y\/¬Z
4) X\/Y\/Z
16











 Математика
Математика Программирование
Программирование








