Похожие презентации:
Применение математического инструментария при решении олимпиадных заданий по обществознанию
1.
Мастер-класс«Применение математического
инструментария при решении олимпиадных
заданий по обществознанию»
2.
Стратегической целью российскогообразования является воспитание
успешного поколения граждан страны,
владеющих адекватными времени
знаниями, навыками и компетенциями,
на идеалах демократии и правового
государства, в соответствии с
национальными и общечеловеческими
ценностными установками
3.
Одаренность- системное, развивающееся в течение
жизни качество психики, которое
определяет возможность достижения
человеком более высоких (необычных,
незаурядных) результатов в одном или
нескольких видах деятельности по
сравнению с другими людьми.
4.
Формы поддержки и работыс одаренными детьми
• проведение школьных интеллектуальных
соревнований: предметных олимпиад, конкурсов,
фестивалей, конференций;
• поддержка участия в региональных и всероссийских
конкурсах, олимпиадах, фестивалях и конференциях;
• организация научных обществ учащихся в
образовательных учреждениях;
• привлечение преподавателей ВУЗов для работы с
одаренными детьми по различным предметным
направлениям.
5.
Олимпиадные задания по обществознаниюможно разделить на несколько типов:
1. Задания с выбором ответа
2. Задания с рядами понятий, имен, фактов общественной жизни
и т.д.
3. Выбор из перечня перечне элементов по определенным
критериям
4.Работа с обществоведческими терминами
5. Работа с иллюстративным рядом
6. Работа с картой.
7. Работа со схемами, с таблицами, графиками и диаграммами по
анализу приведенных данных
8. Работа с текстовыми и другими источниками социальной
информации
9. Обществоведческие задачи (правовые, социологические,
политологические, экономические, логические)
10. Сочинение-эссе.
6.
Включение логических заданий в олимпиады пообществознанию обусловлено тремя важными
обстоятельствами
• Во-первых, знание общих принципов и законов
рационального мышления является неотъемлемым
требованием при изучении темы «Познание».
• Во-вторых, базисные логические знания и навыки
входят в ядро методологии общественных наук, и
без них невозможно представить себе никакое
рациональное исследование общества.
• В-третьих, логические задания обладают большим
методическим потенциалом в части обнаружения,
применения и развития навыков нестандартного,
эвристического мышления.
7.
Проблемы:1.Отсутствие в школьной программе отдельного
предмета «Логика».
2.Требуются знания и связь с другими дисциплинами,
такими как:
• алгебра (метод абстрактного символического
представления знаний),
• геометрия (аксиоматический метод, понятие
доказательства),
• информатика (понятие алгоритма, базовая алгебра
логики, основы комбинаторики),
• история (системный подход, модельное мышление)
• русский язык и литература (культура речи, основы
риторики).
8.
Решение проблемы:Выяснить способы и методы, с
помощью которых можно
решать различные логические
задачи на олимпиадах по
обществознанию с
минимальными временными
затратами.
9.
Типы логических заданий:1. Задания на понимание логической
формы (связанные с умением
правильно определять число
отрицаний в высказывании,
отличать логический смысл союзов
(и/или, если/только если), кванторов
(все/некоторые) и модальных
операторов (необходимо/возможно,
разрешено/запрещено) и т. д.);
10.
Закона двойного отрицания:Предполагается знание одного из
фундаментальных законов классической
логики: отрицание отрицания даёт
утверждение, или: повторенное
дважды отрицание даёт
утверждение.
Например: «Если неверно, что
Вселенная не является
бесконечной, то она бесконечна».
11.
Задача «Учитель»Учитель не стал дезавуировать отказ
от запрета использования шпаргалок
во время экзамена.
Означает ли это, что он разрешил
использование шпаргалок?
12.
Задача «Учитель»Решение: Учитель не стал
дезавуировать отказ от запрета
использования шпаргалок во время
экзамена.
Отрицаний 4, значит, они все
сократятся. Он за использование
шпаргалок.
Ответ: (1) Да,
13.
Типы логических заданий:2. Задания на выведение
правильного заключения из
предложенных посылок (они могут
быть как открытыми, так и
закрытыми);
14.
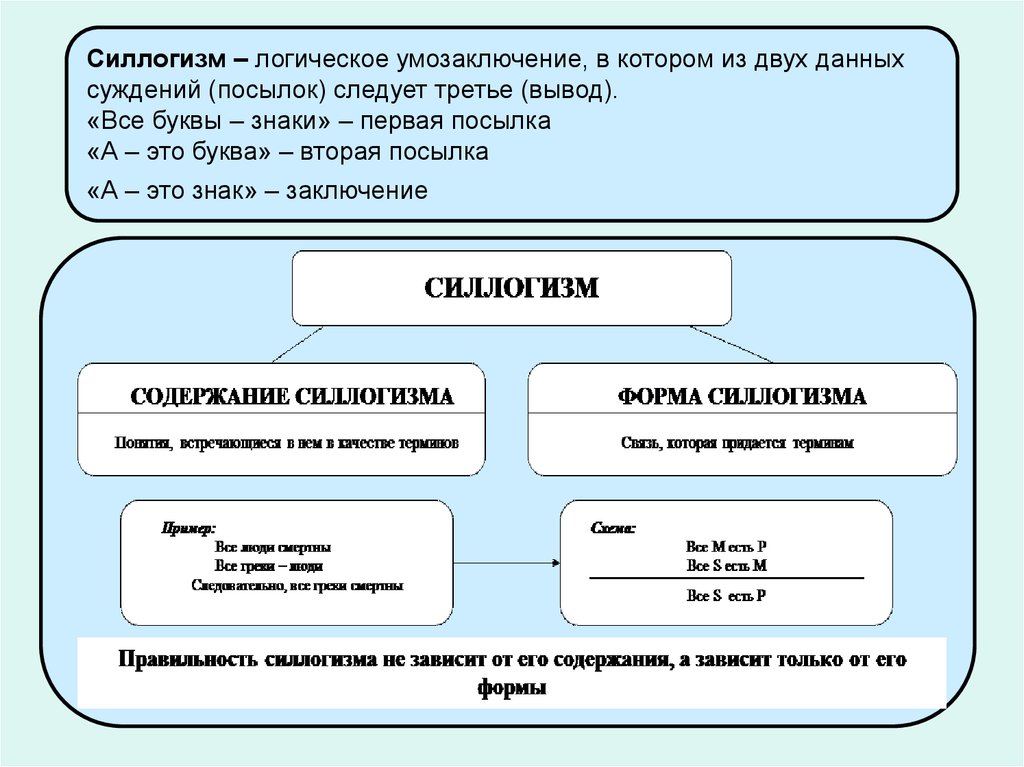
Силлогизм – логическое умозаключение, в котором из двух данныхсуждений (посылок) следует третье (вывод).
«Все буквы – знаки» – первая посылка
«А – это буква» – вторая посылка
«А – это знак» – заключение
15.
Задача «Типичный силлогизм»:1). Всякое преступление (М) есть
правонарушение (Р)
2). Кража (S) есть преступление (М)
3). Следовательно, кража (S) есть
правонарушение (Р)
16.
Типы логических заданий:3. Задания на установление
соответствия (где, исходя из
заданной на множестве объектов
системе свойств и отношений
(«старше», «моложе», «начальник»,
«коллега», «отец» и т. д.),
необходимо определить, кто есть
кто);
17.
Задача «Трое друзей»Беседуют трое друзей: Степанов,
Иванов, Петров.
Ваня сказал Степанову:
«Любопытно, один из нас Иван,
Другой – Петр, третий Степан, но
ни у кого имя не соответствует
фамилии». Как звали каждого
друга?
18.
Решение логических задач спомощью таблиц
Степан
Степанов
Иванов
Петров
Иван
Петр
19.
Решение логических задач спомощью таблиц
Степан
Степанов
Иванов
Петров
Иван
Петр
-
20.
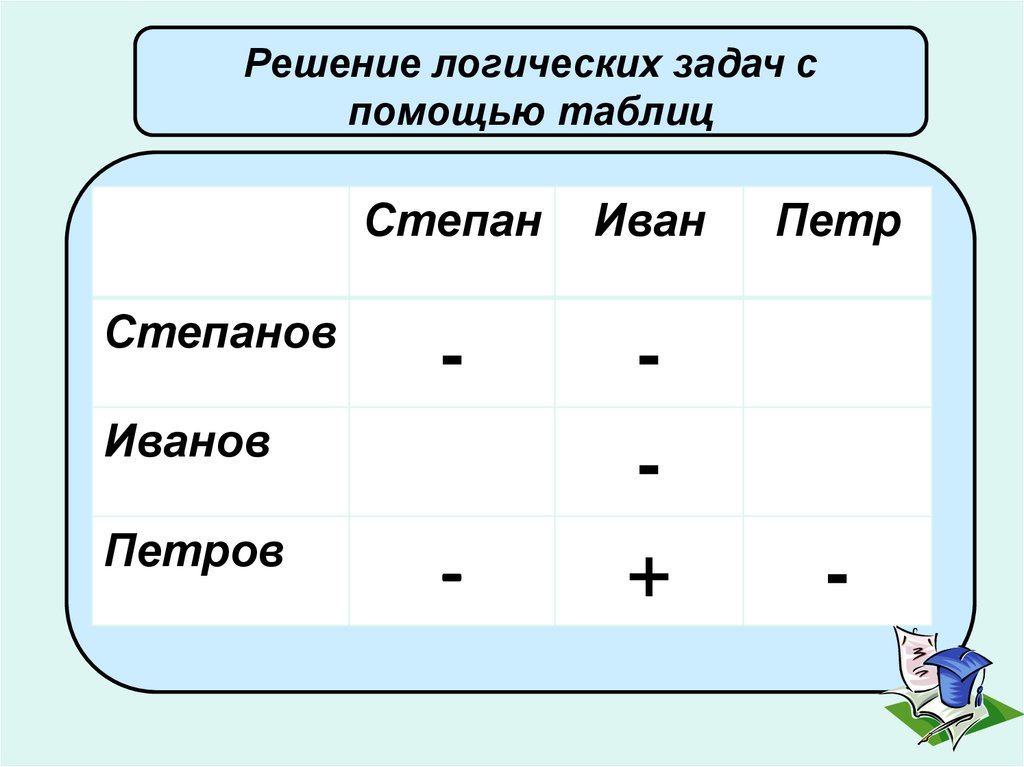
Решение логических задач спомощью таблиц
Степанов
Степан
Иван
Петр
-
+
-
Иванов
Петров
-
21.
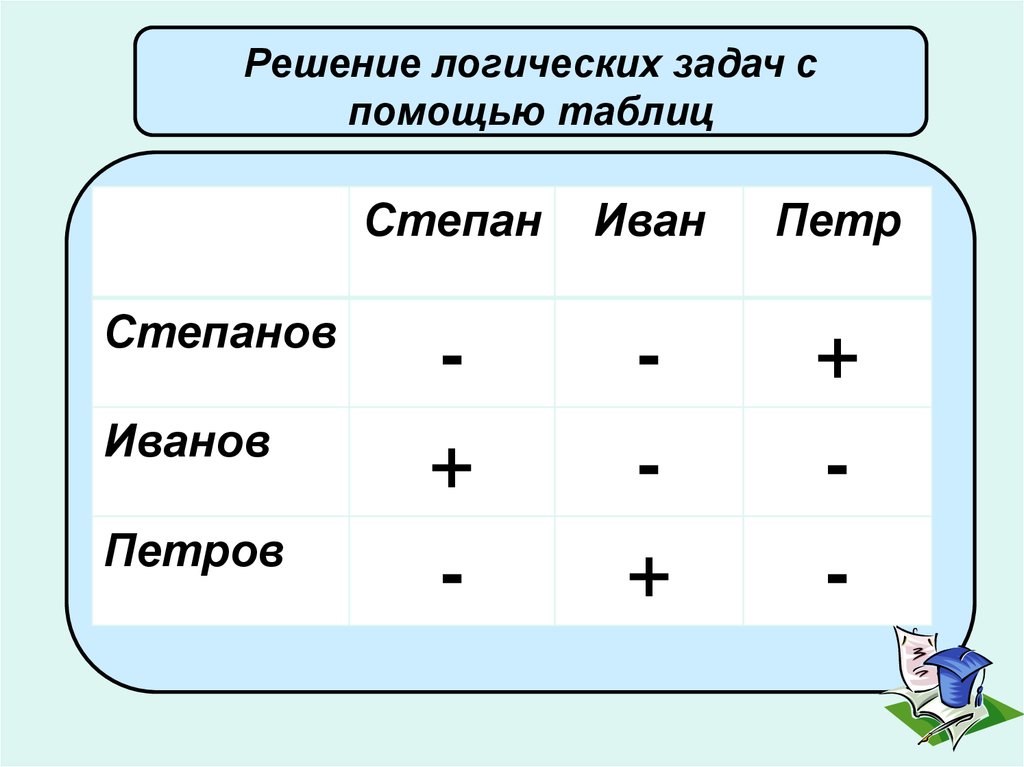
Решение логических задач спомощью таблиц
Степанов
Иванов
Петров
Степан
Иван
Петр
+
-
+
+
-
22.
Типы логических заданий:4.Задания с рекурсивными
условиями (когда одни
высказывания ссылаются на другие,
другие — на третьи, и т. д., что
приводит к возникновению сложной
системы логических
взаимозависимостей между
сравнительно простыми по своему
содержанию высказываниями)
23.
Задача: «Странная семья»В семье четверо детей, причем все
мальчики в ней (если таковые есть)
лгут, а все девочки (если таковые
есть) говорят правду. Один ребенок
сказал: «У меня сестер и братьев
поровну», другой: «У меня ровно один
брат», третий: «У меня ровно два
брата», четвертый: «У меня ровно
две сестры». Определите, сколько в
этой семье мальчиков.
24.
Решение методом «от противного»:1. Допустим, что первый ребенок – девочка. Тогда её
высказывание должно быть истинным, но это
невозможно, т.к. в семье четное число детей и ни у
одного ребенка не может быть братьев и сестер
поровну. Следовательно, первый ребенок – мальчик.
2. Допустим, что второй ребенок – девочка. Тогда её
высказывание должно быть истинным, т.е. у нее
должен быть один брат и две сестры. Поскольку
первый ребенок уже точно является мальчиком (см.
выше), девочками должны быть дети № 3 и № 4. Но
при таких условиях ребенок № 3 не может быть
девочкой, т.к. говорит явную ложь: «У меня ровно
два брата». Противоречие. Следовательно, второй
ребенок – мальчик.
25.
Решение методом «от противного»:3. Поскольку двое детей уже точно являются
мальчиками, высказывание четвертого ребенка «У
меня ровно две сестры» заведомо ложно.
Следовательно, четвертый ребенок – тоже
мальчик.
4. В таком случае уже трое детей гарантированно
являются мальчиками, и, следовательно,
высказывание третьего ребенка «У меня ровно два
брата» заведомо ложно. Значит, он тоже является
мальчиком.
Ответ: В семье 4 мальчика
26.
Типы логических заданий:5. Задания на нестандартное
мышление (содержащие какойлибо логический «подвох»,
который требуется выявить,
или стереотип, который
следует преодолеть).
27.
Задача «Три шкатулки»Перед вами три непрозрачные
шкатулки. В каждой из них лежит
либо миллион рублей, либо один
рубль. Точнее говоря, рубль лежит в
шкатулке, только если надпись на
ней истинна, а миллион – только
если надпись на ней ложна.
Количество истинных и ложных
надписей никак не регламентировано:
может быть, они все истинные, а
может быть, все ложные.
28.
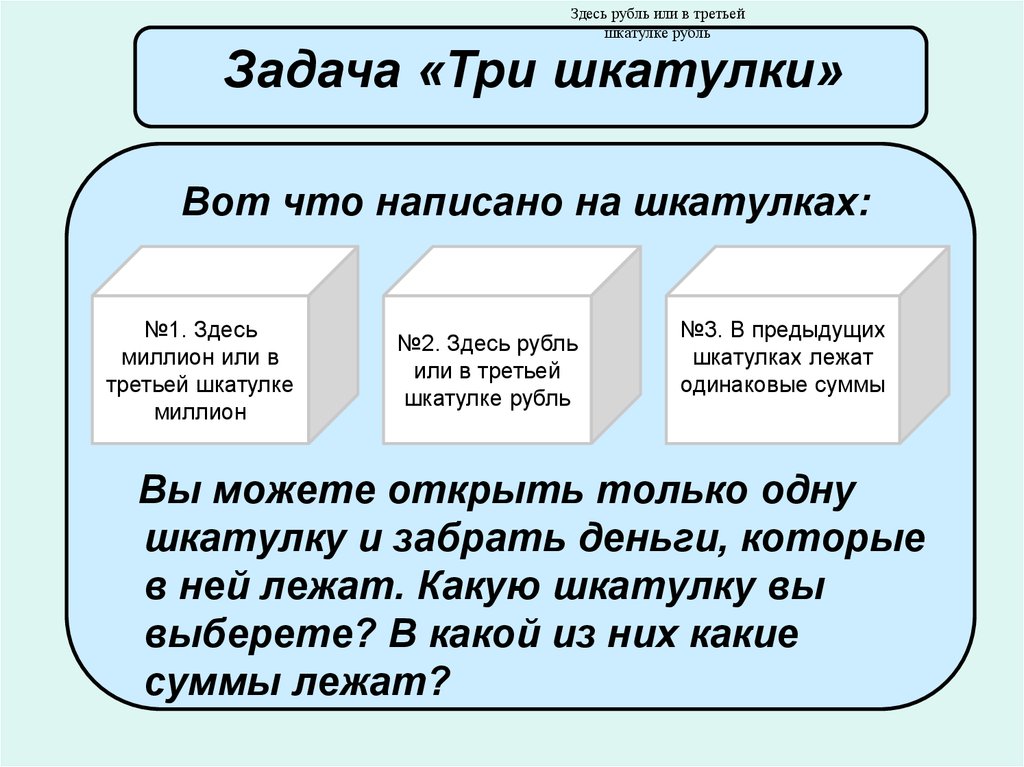
Здесь рубль или в третьейшкатулке рубль
Задача «Три шкатулки»
Вот что написано на шкатулках:
№1. Здесь
миллион или в
третьей шкатулке
миллион
№2. Здесь рубль
или в третьей
шкатулке рубль
№3. В предыдущих
шкатулках лежат
одинаковые суммы
Вы можете открыть только одну
шкатулку и забрать деньги, которые
в ней лежат. Какую шкатулку вы
выберете? В какой из них какие
суммы лежат?
29.
Решать методом «от противного»Ключ к задаче:
1) Допустим, в 1 шкатулке миллион. Значит, надпись на ней
ложна: ни в 1, ни в 3 шкатулке миллиона нет (союз «или»
дает ложь, только если оба связанные им предложения
ложны). Получаем противоречие. Значит, наше допущение
было неверным – на самом деле, в 1 шкатулке рубль.
2) Поскольку в 1 шкатулке рубль, 1 надпись истинна (по
условию). То есть миллион действительно в 1 или в 3. Но
в 1 точно не миллион, как мы уже установили (см. шаг 1).
Следовательно, миллион в 3.
3) Поскольку в 3 шкатулке миллион, надпись на ней должна
быть ложной (по условию). Это значит, что в 1 и 2 не
одинаковые суммы. А поскольку мы уже знаем, что в 1
шкатулке рубль, получается, что во 2 шкатулке не рубль
(т.е. миллион, так как других вариантов, согласно
условию, нет).
30.
Типы логических заданий:6. Задания на когнитивное
моделирование (предполагающие
умение не только строить
собственные рассуждения «от
первого лица», но и одновременно
моделировать рассуждения других
участников познавательной
ситуации, их представления о том,
что кому из них известно и т. д. —
например, классические задачи про
«мудрецов в колпаках»)
31.
Задача «Три профессора»Три профессора логики – Иванов, Петров и Сидоров, –
участвуют в интеллектуальном конкурсе. Пока у них
завязаны глаза, им надевают на головы колпаки (по
условиям игры, имеются три красных колпака, один синий
и один зеленый; оставшиеся после распределения колпаки
убирают так, чтобы их было не видно участникам). Когда
повязки сняты, каждый из них может видеть, какого
цвета колпаки на соперниках, но не на нем самом. После
этого наступает первая фаза игры – каждый из них
должен произнести одно истинное утверждение о том,
что ему стало известно (из непосредственных
наблюдений или из реплик других игроков). Естественно,
игроки прекрасно слышат друг друга. Когда все
высказались, наступает вторая фаза: каждый должен
написать на бумаге ответ, какого цвета колпак у него
самого. Видеть ответы друг друга они уже не могут.
32.
Задача «Три профессора»Вот что сказали участники во время первой фазы
1). Иванов: на мне не зеленый колпак.
2). Петров: на мне не красный колпак.
3). Сидоров: на мне не синий колпак.
Вопросы:
1) У кого из них какой колпак? 2) Все ли игроки смогли
узнать цвет своего колпака? Если да, то в каком
порядке? 3) Если бы реплики игроков шли в
обратном порядке, какими был бы ваш ответ на 1
вопрос? 4) Если бы реплики игроков шли в обратном
порядке, какими был бы ваш ответ на 2 вопрос?
33.
Решение1) Иванов мог понять, что у него не зеленый колпак, только
если увидел одного из своих соперников в зеленом
(методом исключения). Заметим, что после реплики
Иванова тот, у кого зеленый колпак (Петров или Сидоров)
моментально узнает об этом (увидев, что у остальных
не зеленые колпаки, он приходит к выводу, что зеленый
колпак может быть только на нем самом).
2) Реплика Петрова свидетельствует о том, что он уже
узнал, какого именно цвета у него колпак. Ведь из одних
лишь непосредственных наблюдений этот вывод никак не
сделать (красных колпаков три!) – значит, он основан не
только на наблюдениях, а на реплике Иванова. Как уже
было сказано, из его реплики можно узнать только одну
вещь – что у тебя зеленый колпак (когда ты видишь
третьего игрока не в зеленом). Итак, Петров в зеленом
колпаке и знает это.
34.
Решение3) Поскольку Сидоров, в отличие от Петрова, из
прозвучавших реплик свой ответ вывести не мог (это
легко показать перебором вариантов), его реплика
свидетельствует о том, что он видит перед собой когото в синем колпаке (по аналогии с шагом 1). Поскольку
Петров в зеленом, остается признать, что Иванов в
синем. Конечно, после реплики Сидорова сам Иванов это
мгновенно понимает.
4) Таким образом, Петров и Иванов уже знают, какие у них
колпаки. Знает ли Сидоров? Конечно, причем он узнал об
этом раньше всех (до анализа реплик). Поскольку синий и
зеленый колпаки, которые он видит на соперниках, даны в
одном экземпляре, он легко понимает, что у него красный
колпак. Итак, все три профессора знают, какие у них
колпаки. (Сидоров >> Петров >> Иванов)
35.
Решение5) Если бы реплики шли в обратном порядке, то вывод
Петрова опирался бы не на реплику Иванова, а на реплику
Сидорова. Это меняет ответ, хотя сам ход рассуждения
остается прежним. При наличии существенных ошибок и
пробелов в обосновании рассуждения не засчитываются.
При наличии незначительных неточностей и/или легко
восстанавливаемых из контекста пробелов в
обосновании рассуждения могут быть засчитаны
частично.
Ответы:
1) Иванов – синий, Петров – зеленый, Сидоров – красный.
2) Сидоров >> Петров >> Иванов.
3) Иванов – красный, Петров – синий, Сидоров – зеленый.
4) Иванов >> Петров >> Сидоров
36.
При решении логических задач следуетучесть критерии решения:
1. Задача считается решенной полностью
только при наличии правильного ответа и
исчерпывающего обоснования.
2. Всевозможные схемы, таблицы, графики,
разметки не считаются обоснованием, если
не сопровождаются четко
сформулированной последовательностью
умозаключений
37.
Часто встречающиеся ошибки:1. Неправильно проанализирована логическая
форма.
2. Утверждаемое заключение не следует
логически из посылок.
3. Пробел в рассуждениях.
4. Подмена логических обоснований
психологическими (или любыми другими,
нерелевантными сути задачи)
рассуждениями.
5. Подмена логических обоснований примерами
или иллюстрациями.
38.
ЗаключениеЗадача учителя, который готовит
одаренного ребенка к олимпиаде – не
завалить его огромным количеством
материала, а научить самостоятельно
применять минимальный набор
фактических знаний!
39.
РефлексияДискуссия по
результатам совместной
деятельности Мастера и
слушателей.
40.
Список использованных источников:1. Богомолова О.Б. Логические задачи. – М.: БИНОМ, 2013. – 277с.
2. Вечканов В. Шпаргалка по логике. – М., 2006. –90 с.
3. Всероссийская олимпиада школьников. [Электронный ресурс]:
офиц. сайт. - ФГАОУ ДПО АПК и ППРО, 2014-2017. - Режим
доступа: http:// olymp.apkpro.ru
4. Горбатов В.В. ЛОГИКА: Учебное пособие / Московский
государственный университет экономики, статистики и
информатики. – М., 2005. – 213 с.
5. Ильин Е. П. Психология творчества, креативности, одарённости. Спб.: Питер, 2011, с. 147.
6. Олимпиада для школьников. [Электронный ресурс]. - Режим
доступа: Olimpiada.ru
7. Психология одаренности детей и подростков/ Под ред. Н.С.
Лейтеса. — М.: Издательский центр «Академия», 1996. - 416 с.
8. Федеральный государственный образовательный стандарт:
основное общее образование. [Электронный ресурс]. - Режим
доступа: http://standart.edu.ru/catalog.aspx?CatalogId=2589




































 Математика
Математика Экономика
Экономика








