Похожие презентации:
Енергія, робота та потужність.Закон збереження енергії. Лекція 5
1.
Лекція № 5.Енергія, робота та потужність
Закон збереження енергії
1. Енергія, робота та потужність
2. Кінетична енергія поступального та
обертального рухів
3. Потенціальна енергія. Енергія пружно
деформованого тіла
4. Гравітаційне поле та його характеристики.
Потенціальна енергія матеріальної точки у
гравітаційному полі
5. Потенціальні сили та консервативні системи
6. Закон збереження енергії у механіці
2. 1. Енергія, робота та потужність
Енергія – це скалярнафізична величина, що є
універсальною кількісною
мірою руху і взаємодії усіх
видів матерії. Тіло, що має
енергію
спроможне
виконати роботу.
Е Дж (джоуль ).
3.
4.
Робота – це скалярнафізична величина, що чисельно
дорівнює
скалярному
добутку сили на переміщення:
А F r Fs cos ,
[ A] Дж H м.
Для змінної сили робота дорівнює
або
dА F ds cos
S
А12 F cos ds .
0
F
r
F
5.
6.
Потужність – це скалярна фізична величина,що характеризує роботу системи, яку вона виконує
за одиницю часу:
A
dA Fds
N
F ,
або N
t
dt
dt
Дж
[ N ] Вт
.
с
7.
Якщо система мала у першому стані 1 енергіюЕ1 і переходить у стан 2 з енергією Е2, то A12=E1-E2,
тобто зміна енергії системи іде на виконання нею
роботи.
8. 2. Кінетична енергія поступального та обертального рухів
Кінетична енергія – скалярна фізичнавеличина, що є універсальною кількісною мірою
руху матерії.
9.
Кінетична енергіяпоступальний рух:
тіла,
m
.
2
2
Eк пост
що
здійснює
10.
Оскільки лінійна і кутова швидкості пов’язанізалежністю υ=ω·r, тоді .
mr
Eк
,
2
2
2
або, якщо врахувати, що mr2=I, можна отримати
формулу
кінетичної
енергії
тіла
при
обертальному русі:
I
.
2
2
Eк обер
11.
Повна кінетична енергія тіла, що здійснюєодночасно і поступальний і обертальний рухи:
m
I
Eк
.
2
2
2
2
12. 3. Потенціальна енергія. Енергія пружно деформованого тіла
Потенціальна енергія – скалярна фізичнавеличина, що є універсальною кількісною мірою
взаємодії усіх видів матерії (тіла з іншим тілом чи
полем), визначається взаємним розміщенням тіл
або тіла у полі.
13.
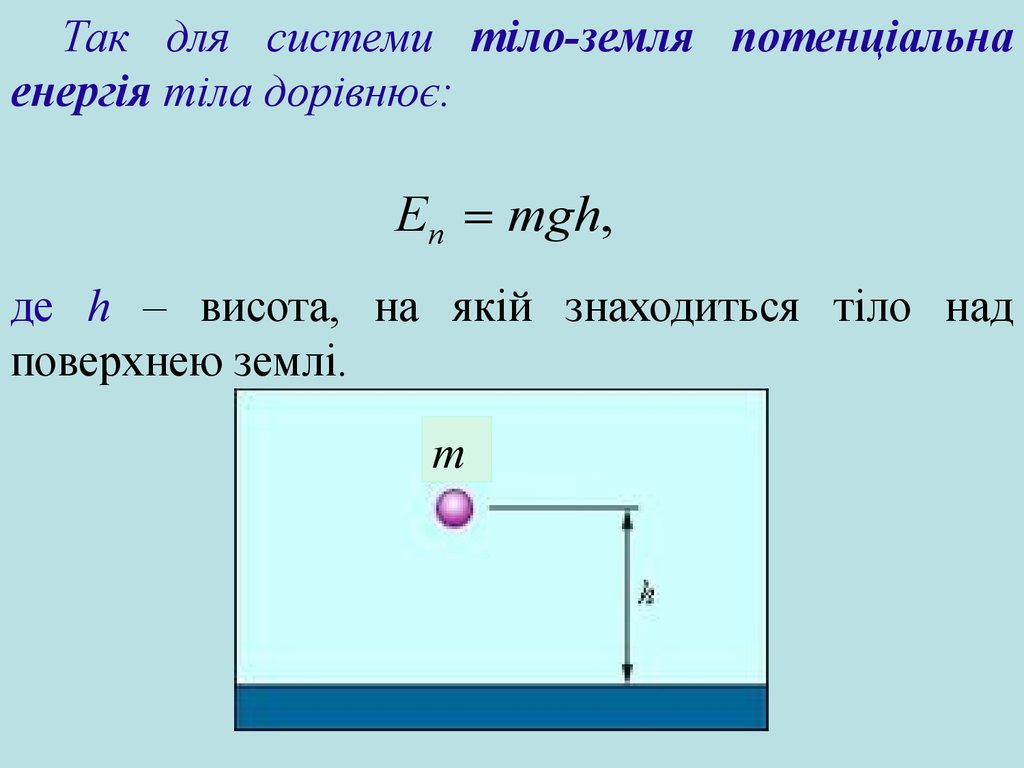
Так для системи тіло-земля потенціальнаенергія тіла дорівнює:
Eп mgh,
де h – висота, на якій знаходиться тіло над
поверхнею землі.
m
14.
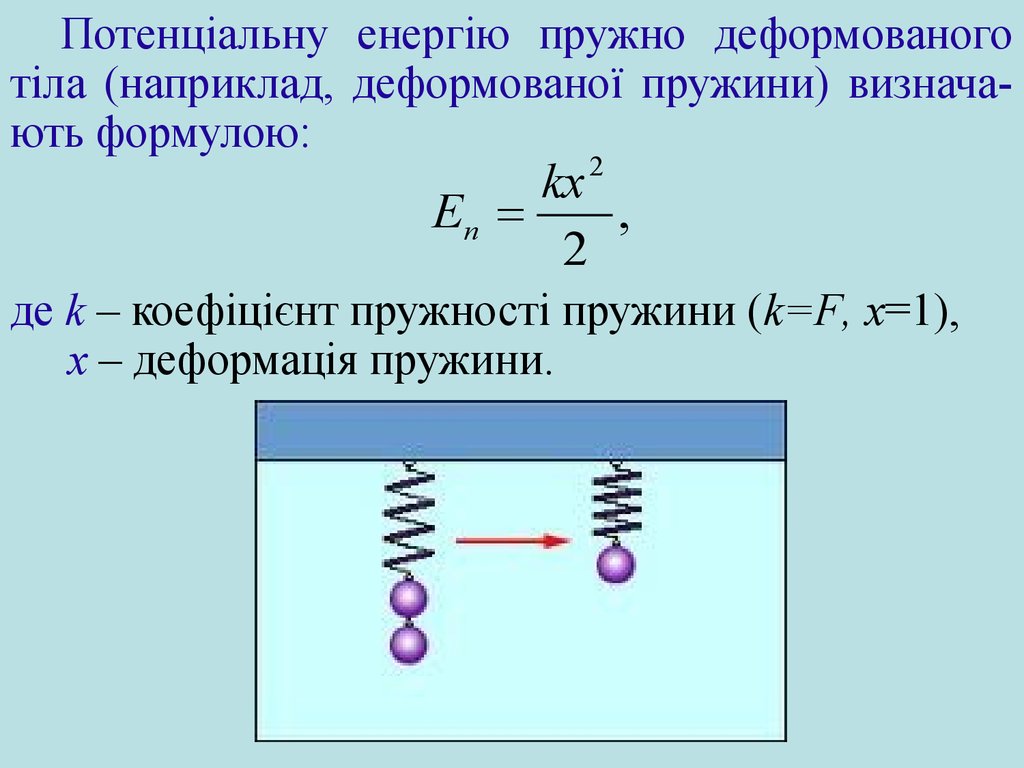
Потенціальну енергію пружно деформованоготіла (наприклад, деформованої пружини) визначають формулою:
2
kx
Eп
,
2
де k – коефіцієнт пружності пружини (k=F, x=1),
x – деформація пружини.
15. 4. Гравітаційне поле та його характеристи-ки. Потенціальна енергія матеріальної точки у гравітаційному полі
4. Гравітаційне поле та його характеристики. Потенціальна енергія матеріальноїточки у гравітаційному полі
Англійський
фізик
Ісаак
Ньютон, вивчаючи рух небесних
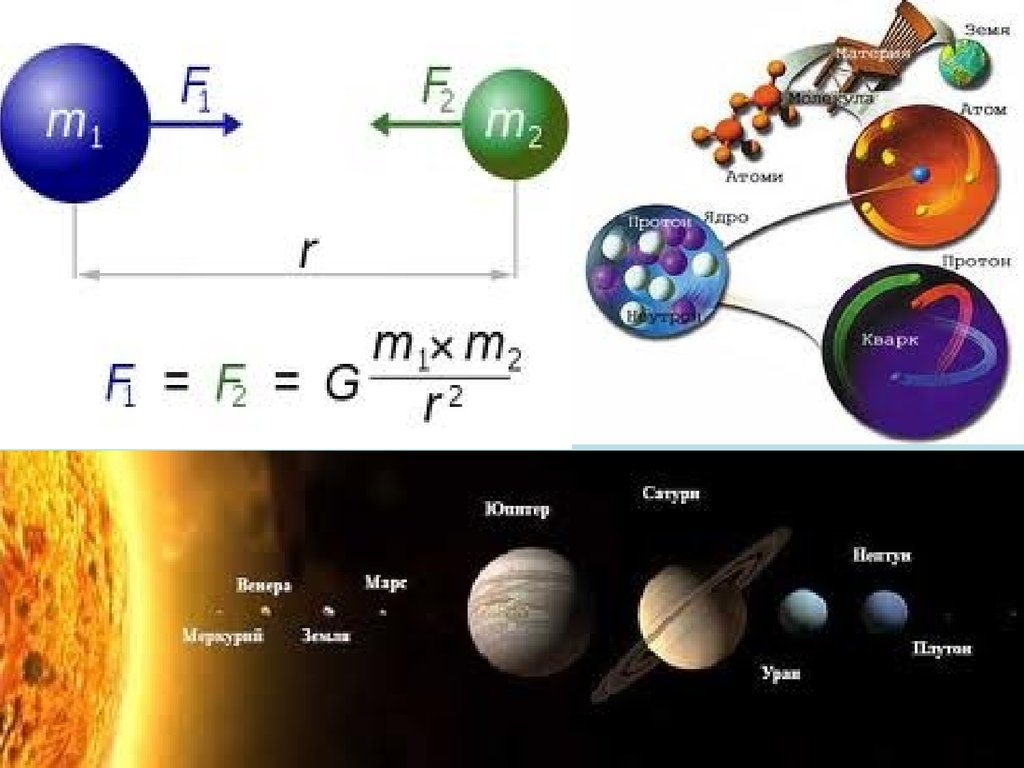
тіл, дійшов висновку, що всі тіла
притягуються одне до одного із
силою, що дорівнює:
m1m2
F G 2 ,
r
3
м
– гравітаційна стала,
2
кг с
де G 6 ,67 10
m1 і m2 – маси тіл,
r – відстань між ними.
12
16. Англ. фізик Генрі Кавендліш експериментально визначив гравітаційну сталу, що дало можливість вперше визначити і масу Землі
17.
18.
Гравітаційна взаємодія між тілами передаєтьсячерез гравітаційне поле – матеріальне середовище,
яке існує навколо тіл і через яке відбувається
взаємодія між тілами.
Для характеристики гравітаційного поля вводять
два параметри:
1) силову характеристику – напруженість поля;
2) енергетичну характеристику – потенціал поля.
19.
1) Напруженість гравітаційного поля Е – цевекторна фізична величина, що є силовою
характеристикою гравітаційного поля та чисельно
дорівнює силі, яка діє на тіло одиничної пробної
маси, внесене
в дану точку поля:
F
Е
,
m0
так як
mm0
F G 2 ,
r
то
m
E G 2.
r
F m0
m
r
20.
Оскільки сила, з якою Земля притягує до себетіла поблизу своєї поверхні дорівнює
F mg, а з
іншого боку за законом всесвітнього тяжіння
Mз .
M з m, то
Mз m і
F G
g G 2
mg G
2
2
Rз
Rз
Rз
.
Звідси слідує, що напруженість гравітаційного поля
Землі чисельно дорівнює прискоренню вільного падіння:
E землі g .
21.
2) Потенціал гравітаційного поля φ – цескалярна фізична величина, що є енергетичною
характеристикою гравітаційного поля та чисельно
дорівнює відношенню потенціальної енергії
гравітаційного поля до пробної маси m0:
Eп
.
mo
m
Eп m0
r
22.
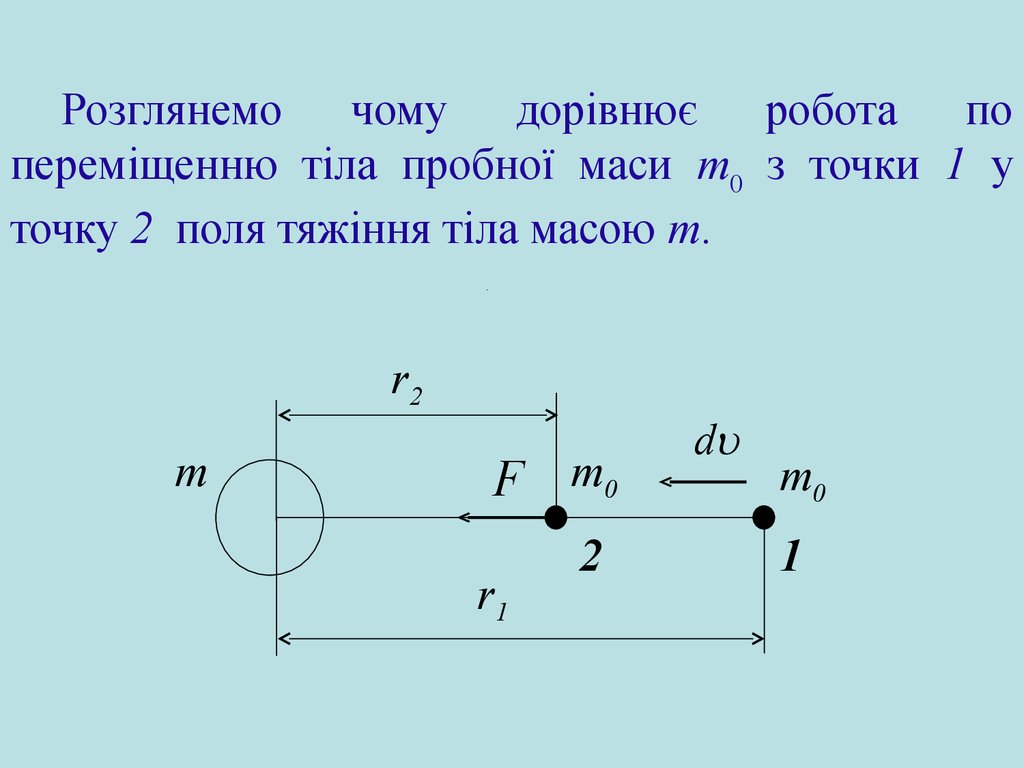
Розглянемочому
дорівнює
робота
по
переміщенню тіла пробної маси m0 з точки 1 у
точку 2 поля тяжіння тіла масою m.
r2
m
F m0
r1
2
d
m0
1
23.
Елементарна робота дорівнює, де
dА F ds
, тобто є функцією відстані r.
mm0
F G 2
Отже: r
mmo
.
dА G
r
2
dr.
Проінтегрувавши даний вираз в межах від r1 до r2
отримаємо повну роботу
r1
mm0 mm0
mm0
mm0
mm0
G
А12 G 2 dr G
G
r
r1
r1
r2
r2
r2
З іншого боку, виконана над тілом робота
дорівнює зміні його потенціальної енергії:
А12 Eп1 Eп2 .
24.
Потенціальна енергія тіла масою m0 у політяжіння Землі дорівнює:
mm0
Еп G
.
r
Тоді потенціал гравітаційного поля у даній точці
дорівнюватиме:
m
G .
r
25.
Потенціал φ і напруженість гравітаційного поляE пов’язані між собою рівнянням:
d
Е
dr
де знак
“–“
показує,
що
вектор
напруженості
поля Е протилежно направлений до зростання
d
потенціалу dφ, величину
називають градієнтом
dr
потенціалу, вона показує зміну потенціалу з
одиницею довжини.
У математиці вводять операторgrad i x j y k z,
тобто:
grad E.
26. Гравітаційні сили порівняно слабкі, наприклад, вони значно слабкіші за електричні. Однак сили гравітації стають відчутними для космічних
Гравітаційні сили порівняно слабкі, наприклад,вони значно слабкіші за електричні. Однак сили
гравітації стають відчутними для космічних тіл
великих мас: планет або зірок, а також відіграють
основну роль в формуванні зір і планетних систем
із туманностей тощо.
Справедливість закону
всесвітнього
тяжіння
продемонстровано
на
рисунку, де зображено одне
з найкрасивіших небесних
видовищ – кульове зоряне
скупчення М13 у сузір’ї
Геркулес, кожна точка якого
– це зоря.
27. 5. Потенціальні сили та консервативні системи
Силу, що діє на матеріальнуточку або на тіло, яке рухається
поступально, називають консервативною
або
потенціальною
силою, якщо робота
A1-2, яка
виконується під дією цієї сили при 1
переміщенні точки (тіла) з одного
довільного положення 1 в інше 2,
не залежить від форми траєкторії,
вздовж
якої
відбулось
це
переміщення:
A1-a-2=A1-b-2=A1-2.
2
a
b
28.
Зміна напрямку руху вздовжтраєкторії
на
протилежний
спричинює зміну знака роботи
(кут замінюється на π-α і cos
змінює свій знак). Тому робота
консервативної
сили
при
переміщенні матеріальної точки 1
вздовж замкненої траєкторії L (1а-2-b-1) тотожно дорівнює нулю:
( F , dr ) A1 a 2 A2 b 1 0.
L
2
a
b
29.
Прикладами консервативних сил можуть бутисили тяжіння, гравітаційні сили, сили пружності,
сили електростатичної взаємодії між зарядженими
тілами.
Прикладами неконсервативних сил є сили тертя,
сили опору середовища.
30.
Механічні системи, на тіла яких діють тількиконсервативні сили, називають консервативними
системами (в них можуть відбуватися тільки
перетворення кінетичної енергії в потенціальну і
навпаки в еквівалентних кількостях, так що повна
механічна енергія залишається сталою).
Дисипативні системи – це системи, в яких
механічна енергія поступово зменшується за
рахунок перетворення в інші (немеханічні) форми
енергії (у системі, в якій діють такі
неконсервативні сили, наприклад сили тертя, повна
механічна енергія системи не зберігається, але при
цьому завжди виникає еквівалентна кількість
енергії іншого виду).
Таким чином, енергія ніколи не зникає і не
з'являється знову, вона тільки переходить з
одного виду в інший.
31. 6. Закон збереження енергії у механіці
Повна енергія тіла складається з• кінетичної,
• потенціальної,
• внутрішньої.
32.
Енергія системи не може самовільно виникнутиабо безслідно зникнути, вона може лише перерозподілятися між тілами системи чи переходити з
одних видів у інші – закон збереження
механічної енергії.
33.
Для системи, в якій відсутні сили тертя абоопору (консервативна система), сума кінетичної і
потенціальної енергії є величиною сталою – закон
збереження механічної енергії для консервативних систем:
n
E
i 1
n
кi
E n i const
i 1
Еп
Ек
або
n
mi
I i
En i const.
2
2
i 1
i 1
i 1
n
2
i
n
2
i
34.
35.
Лекція № 5.Енергія, робота та потужність
Закон збереження енергії
1. Енергія, робота та потужність
2. Кінетична енергія поступального та
обертального рухів
3. Потенціальна енергія. Енергія пружно
деформованого тіла
4. Гравітаційне поле та його характеристики.
Потенціальна енергія матеріальної точки у
гравітаційному полі
5. Потенціальні сили та консервативні системи
6. Закон збереження енергії у механіці































 Физика
Физика








