Похожие презентации:
Динамический характер адсорбции. Лекция 2
1. Лекция 2 Динамический характер адсорбции
Основные темы:-Динамический характер адсорбции на
поверхности раздела сопредельных фаз.
-Миграция адсорбированных молекул по
поверхности.
-Классические теоретические уравнения
изотерм адсорбции Генри, Ленгмюра,
Фаулера- Гугенгейма, БЭТ и др.
-Оценка площадок, занимаемых адсорбированными молекулами в заполненном
монослое.
1
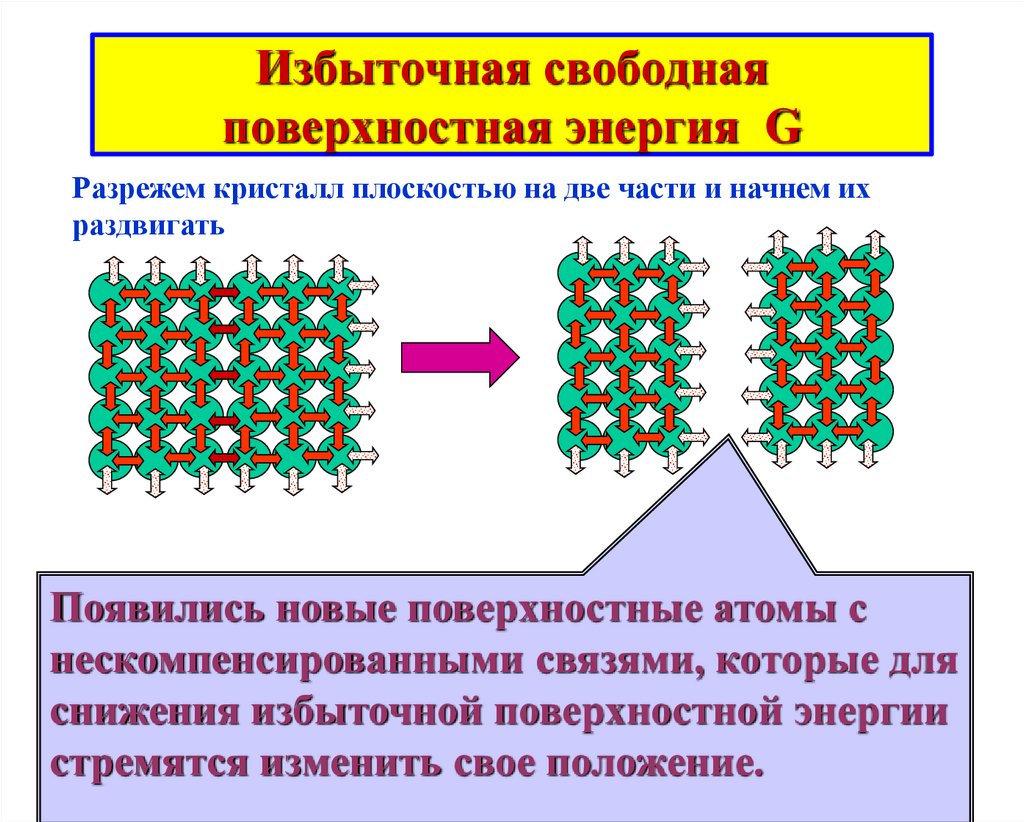
2. Избыточная свободная поверхностная энергия G
Разрежем кристалл плоскостью на две части и начнем ихраздвигать
Появились новые поверхностные атомы с
нескомпенсированными связями, которые для
снижения избыточной поверхностной энергии
стремятся изменить свое положение.
2
3. Избыточная свободная поверхностная энергия F
Приповерхностная зона может перестраиваться.Перестройка захватывает несколько слоев,
осуществляется сравнительно быстро в
жидкостях и медленно – в тв. фазах, зависит от
взаимодействий в объеме, Т , в жидкостях – от
вязкости и т.д.
Наиболее сложна в твердых фазах.
3
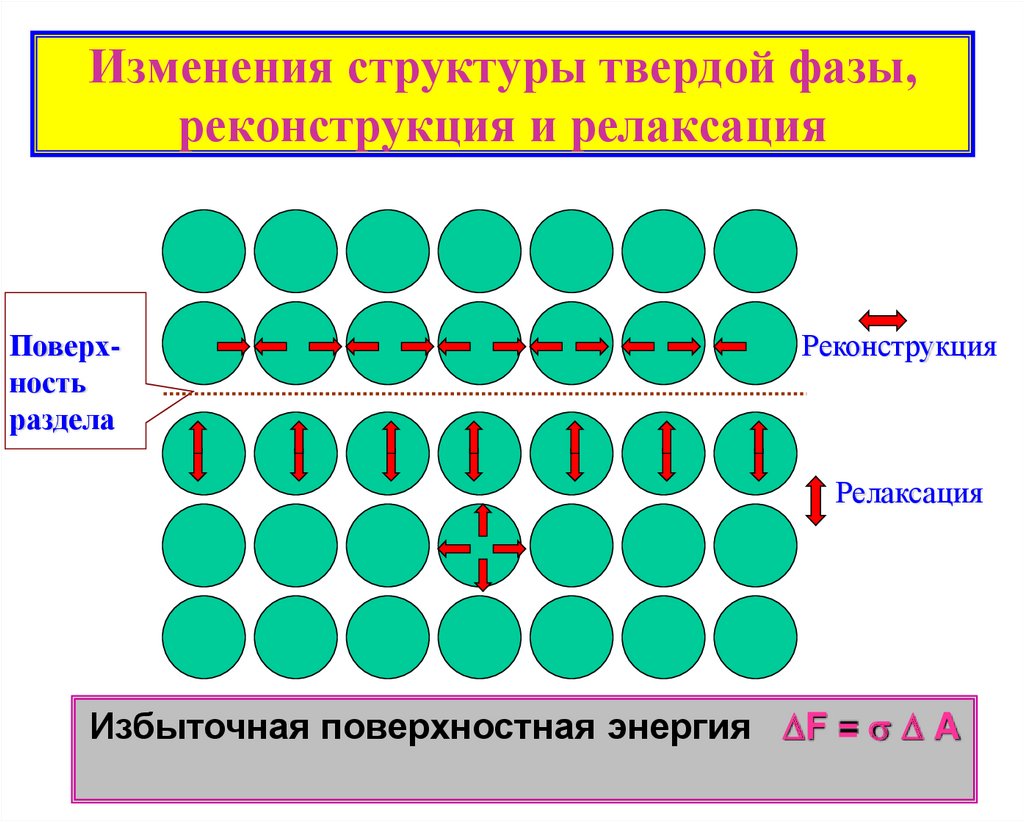
4. Изменения структуры твердой фазы, реконструкция и релаксация
Поверхностьраздела
Реконструкция
Релаксация
Избыточная поверхностная энергия F = A
4
5. Изменения структуры твердой фазы
•Адсорбция изменяет ситуацию наповерхности и также сопровождается
различными типами ее перестройки,
наиболее радикальна при химической
адсорбции, где часто отмечают
реконструктивную хемосорбцию
(например, при хемосорбции О2 на
металлах).
5
6. Изменения структуры твердой фазы
•Поэтому приповерхностная часть адсорбентаи окружающая среда находятся в динамическом равновесии, изменение внешних
условий сопровождается деформациями в
адсорбенте.
•Динамический характер адсорбции еще
более ярко проявляется на поверхности со
стороны газовой фазы.
6
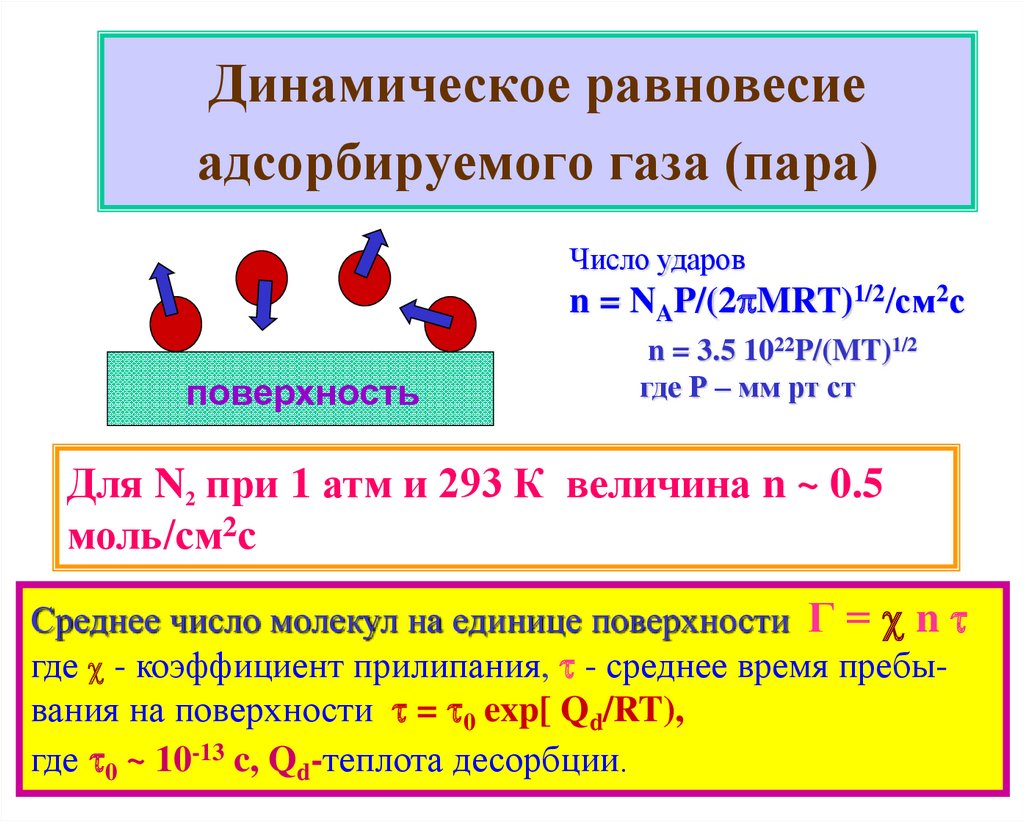
7. Динамическое равновесие адсорбируемого газа (пара)
Число ударовn = NAP/(2 MRT)1/2/см2с
поверхность
n = 3.5 1022P/(MT)1/2
где Р – мм рт ст
Для N2 при 1 атм и 293 К величина n ~ 0.5
моль/см2с
Среднее число молекул на единице поверхности Г = n
где - коэффициент прилипания, - среднее время пребывания на поверхности = 0 exp[ Qd/RT),
где 0 ~ 10-13 c, Qd-теплота десорбции.
7
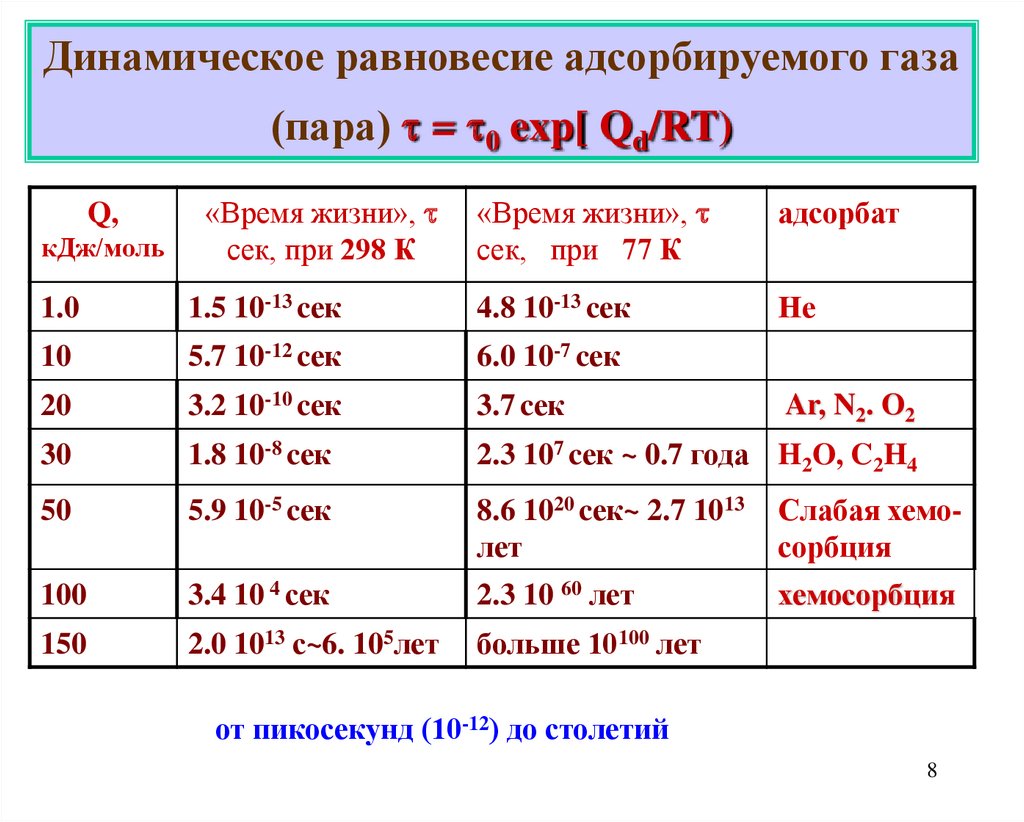
8.
Динамическое равновесие адсорбируемого газа(пара) = 0 exp[ Qd/RT)
Q,
кДж/моль
«Время жизни»,
сек, при 298 К
«Время жизни»,
сек, при 77 К
адсорбат
Не
1.0
1.5 10-13 cек
4.8 10-13 cек
10
5.7 10-12 cек
6.0 10-7 cек
20
3.2 10-10 cек
3.7 cек
30
1.8 10-8 cек
2.3 107 cек ~ 0.7 года H2O, C2H4
50
5.9 10-5 cек
8.6 1020 cек~ 2.7 1013
лет
Слабая хемосорбция
100
3.4 10 4 сек
2.3 10 60 лет
хемосорбция
150
2.0 1013 с~6. 105лет
больше 10100 лет
Ar, N2. O2
от пикосекунд (10-12) до столетий
8
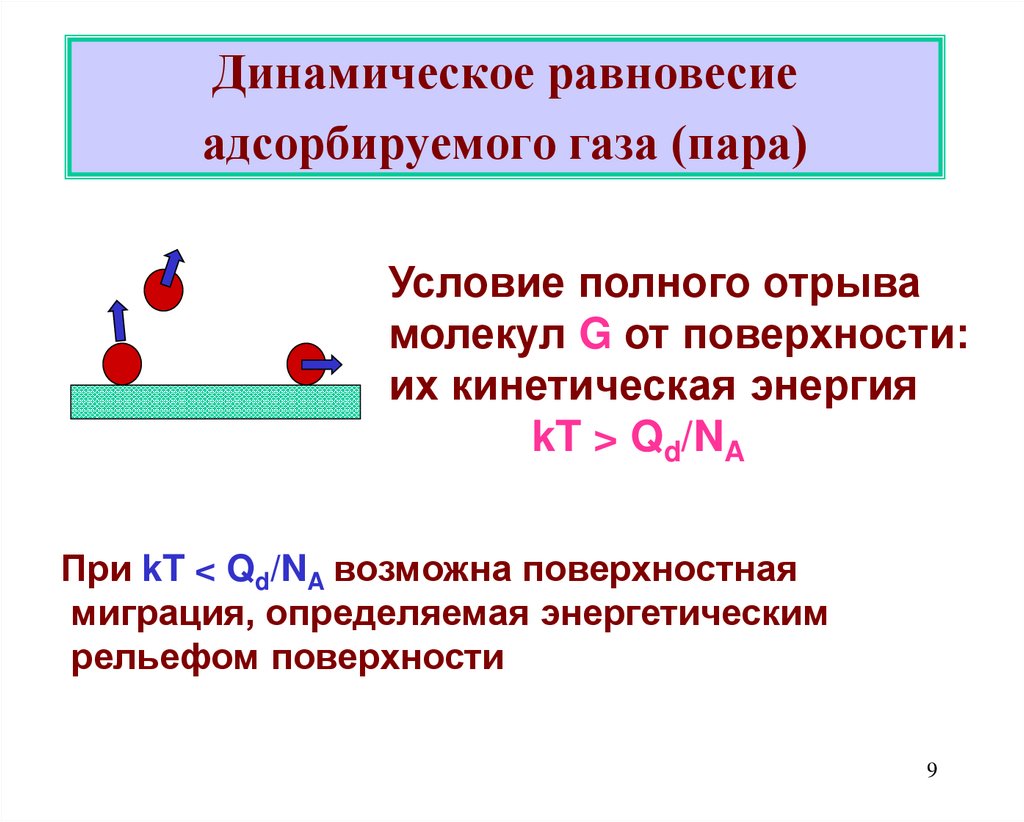
9. Динамическое равновесие адсорбируемого газа (пара)
Условие полного отрывамолекул G от поверхности:
их кинетическая энергия
kT > Qd/NA
При kT < Qd/NA возможна поверхностная
миграция, определяемая энергетическим
рельефом поверхности
9
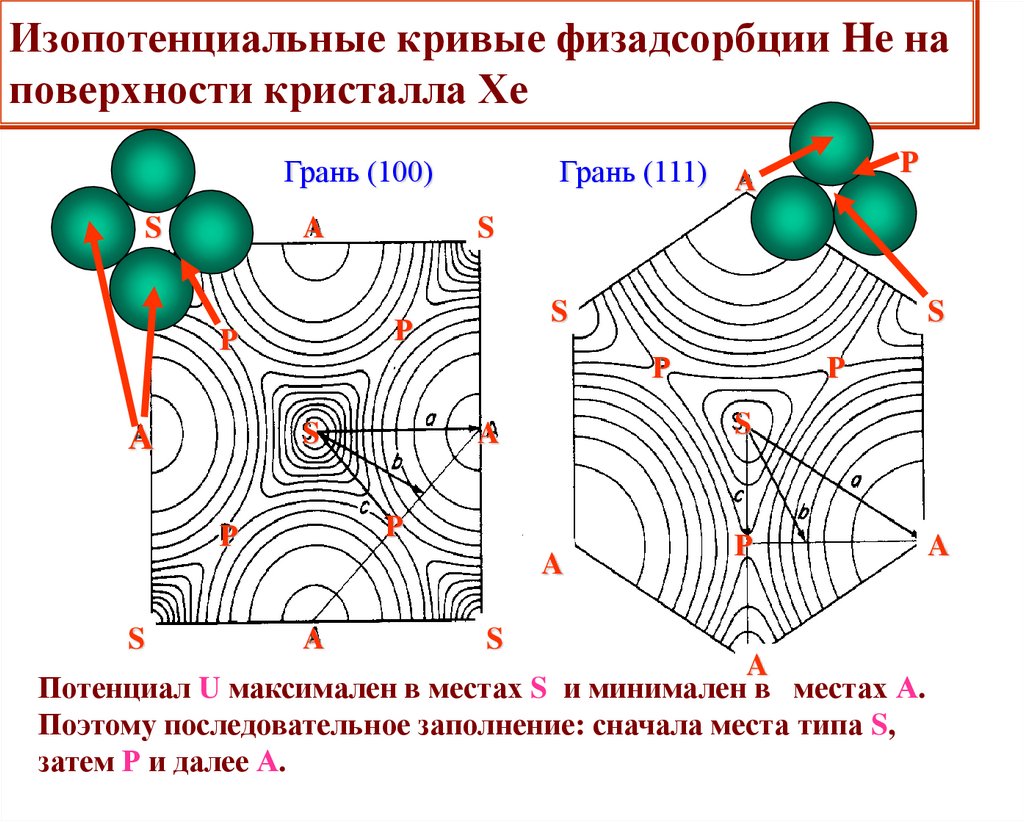
10. Изопотенциальные кривые физадсорбции He на поверхности кристалла Хе
Грань (100)SS
A
S
A
A
S
Р
S
A
Р
Р
S
S
Р
S
A
S
Р
Р
Р
Грань (111) A
Р
A
A
Потенциал U максимален в местах S и минимален в местах А.
Поэтому последовательное заполнение: сначала места типа S,
затем Р и далее А.
10
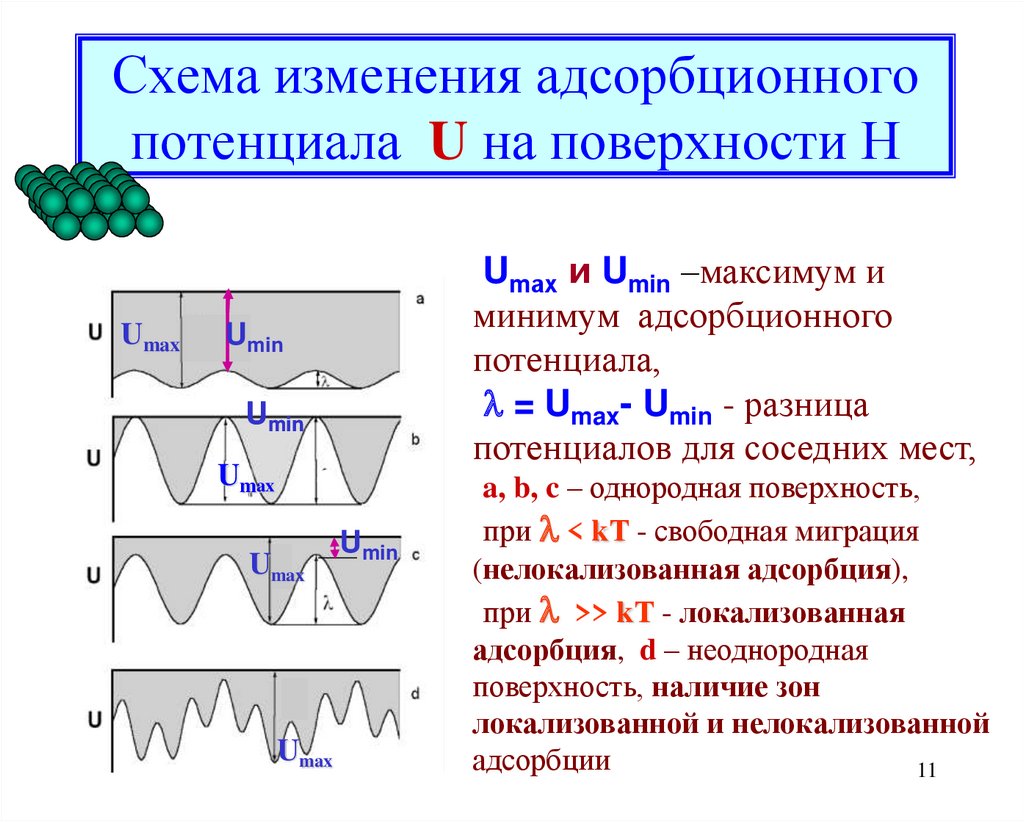
11. Схема изменения адсорбционного потенциала U на поверхности Н
aUmax
Umin
b
Umin
Umax
Umax
Umax
Umin
Umах и Umin –максимум и
минимум адсорбционного
потенциала,
= Umax- Umin - разница
потенциалов для соседних мест,
a, b, c – однородная поверхность,
c при < kТ - свободная миграция
(нелокализованная адсорбция),
при >> kТ - локализованная
d адсорбция, d – неоднородная
поверхность, наличие зон
локализованной и нелокализованной
адсорбции
11
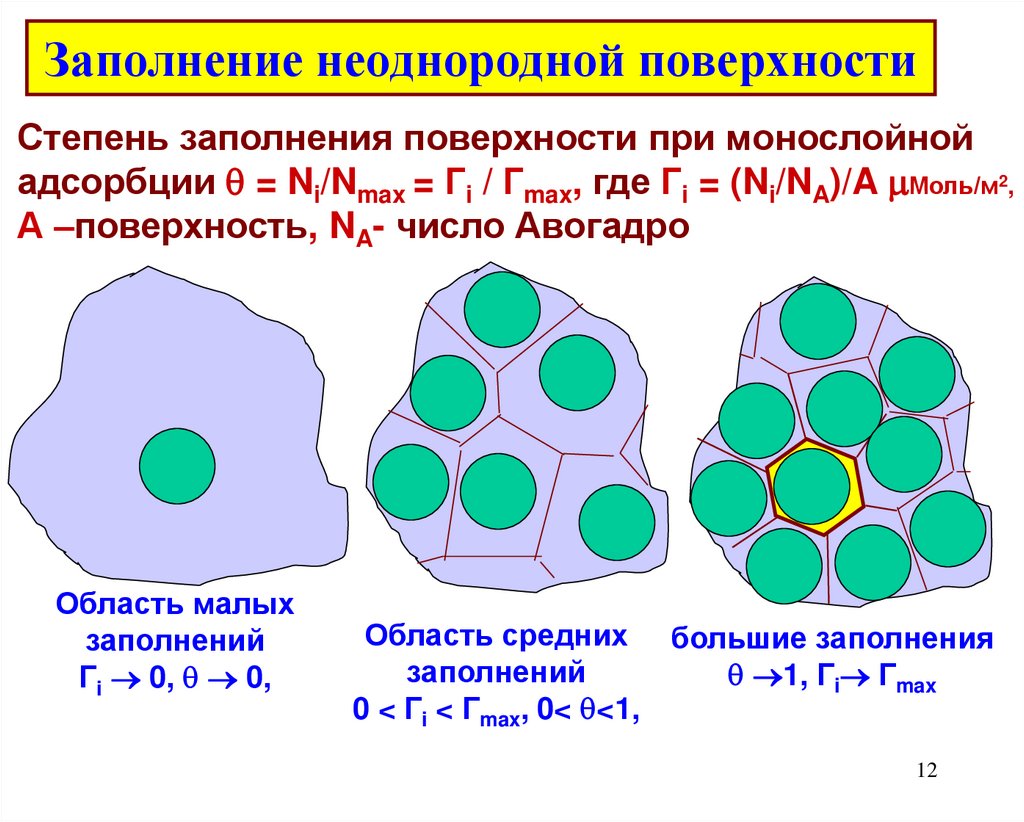
12. Заполнение неоднородной поверхности
Степень заполнения поверхности при монослойнойадсорбции = Ni/Nmax = Гi / Гmax, где Гi = (Ni/NA)/A Моль/м2,
А –поверхность, NA- число Авогадро
Область малых
заполнений
Гi 0, 0,
Область средних большие заполнения
заполнений
1, Гi Гmax
0 < Гi < Гmax, 0< <1,
12
13. Средняя площадка, приходящаяся на одну молекулу в заполненном монослое
Средняя площадка, приходящаяся на однумолекулу в заполненном монослое
Гмах ( Моль/м2) = (Nmax/NA)/A
Обозначим площадку на одну молекулу в
заполненном монослое как
= А/Nmax (размерность: Å2/шт или нм2/шт).
В результате
Гмах= 1/ NA = 166.1/ Моль/м2
Величина удельной поверхности (м2/г)
А = Nmax или А = (аm/NA) , где аm- адсорбция в
заполненном монослое (моль/г):
=Апр/(1- S)
Апр –проекция молекулы на плоскость;
S- доля промежутков между проекциями (двумерная
пористость монослоя, 1- S – доля поверхности, занятая
проекциями адсорбированных молекул)
13
14. Область малых заполнений - изотерма адсорбции Генри
число ударов n = NAP/(2 MRT)1/2/см2суравнение изотермы:
Г
Р
при Т= Const
Г = n ( е Q/RT) = Кг P
0
Г – среднее число молекул на единице
поверхности , Кг – коэффициент Генри,
- коэффициент прилипания.
В этой области межмолекулярное взаимодействие
адсорбат/адсорбат (G/G) пренебрежимо мало и
определяющим является взаимодействие
адсорбат/адсорбент (G/H). Адсорбционные измерения в
области Генри используют для определений
взаимодействия G/H.
Уравнение Генри – предельная форма всех изотерм 14
адсорбции при Р 0 или = Г/Гмах 0,
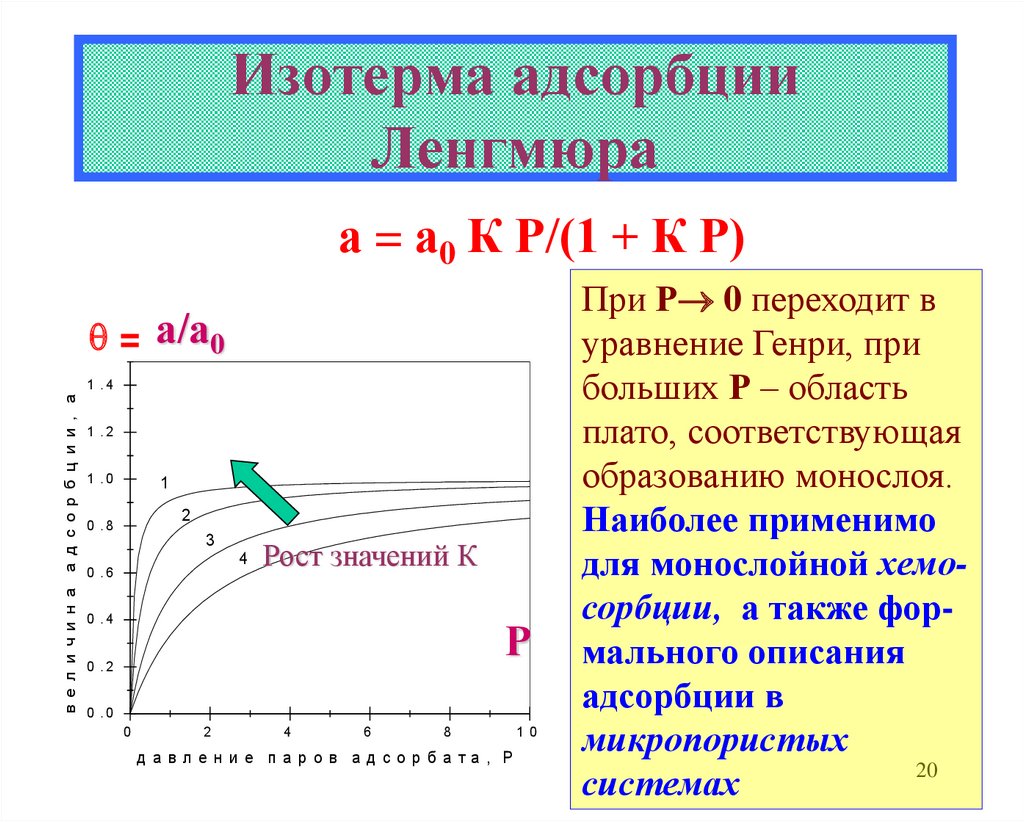
15. Изотерма адсорбции Ленгмюра
•Это уравнение предложил в 1918 гИрвинг Ленгмюр (1881-1957)нобелевский лауреат 1932 г.
По смыслу вывода – это уравнение
мономолекулярной адсорбции на
однородной поверхности без учета
взаимодействия G/G, т.е между
адсорбированными молекулами
15
16. Изотерма адсорбции Ленгмюра
Молекулыгостя G
Вид на поверхность сверху
Поверхность хозяина, H
На поверхности занято = Z/Z0 от общего числа
центров Z0.
Доля свободных центров 1- .
Взаимодействием между адсорбированными
молекулами в этой модели пренебрегают.
16
17. Изотерма адсорбции Ленгмюра
Допущения в модели Ленгмюра• Однородность поверхности (все адсорбционные
центры эквивалентны)
• Адсорбция локализованная, т.е. частицы
адсорбируются в определенных местах поверхности
• Каждый адсорбционный центр может принять
только одну частицу
• Адсорбированные частицы не взаимодействуют
друг с другом
Сформулированные допущения позволяют осуществить строгий вывод
уравнения изотермы Ленгмюра в рамках классической статистической
механики, и следовательно уравнение Ленгмюра не противоречит
термодинамике.
18. Изотерма адсорбции Ленгмюра
Простейший квазихимический вывод:G + [Z] [GZ]
РG (1 - )
[Z] – активный центр на поверхности адсорбента
(хозяина),
[GZ] –образующийся активный комплекс
Скорость прямой реакции ~k1P(1 - )
Скорость обратной реакции ~ k2
Константа равновесия К = /РG(1 - )
18
19. Изотерма адсорбции Ленгмюра
Из К = /Р(1- ) следует= КР/(1 + К Р) = Г/Гмах = а/а0
уравнение Ленгмюра
а = а0 К Р/(1 + К Р)
другие часто используемые формы записи:
= КР/(1 + К Р) или Р = [ /К (1- )]
19
20. Изотерма адсорбции Ленгмюра
а = а0 К Р/(1 + К Р)= а/а0
в е л и ч и н а
а д с о р б ц и и , а
1 .4
1 .2
1 .0
1
2
0 .8
3
0 .6
4
Рост значений К
0 .4
Р
0 .2
0 .0
0
2
4
6
8
д авл ение п аров ад сорб ата, Р
1 0
При Р 0 переходит в
уравнение Генри, при
больших Р – область
плато, соответствующая
образованию монослоя.
Наиболее применимо
для монослойной хемосорбции, а также формального описания
адсорбции в
микропористых
20
системах
21. Изотерма адсорбции Ленгмюра а = а0 К Р/(1 + К Р)
Линеализируется в координатах Р/а = 1/(а0К) + (1/а0)Р;или а/Р = Ка0 - Ка или 1/а = 1/а0 + (1/а0 К) (1/Р ), что
позволяет определять коэффициенты а0 и К,
Последний пропорционален коэффициенту Генри.
Р/а
Р/а=1/(а0К) + (1/а0)Р
tg = а0-1
(а0К)-1`
P
21
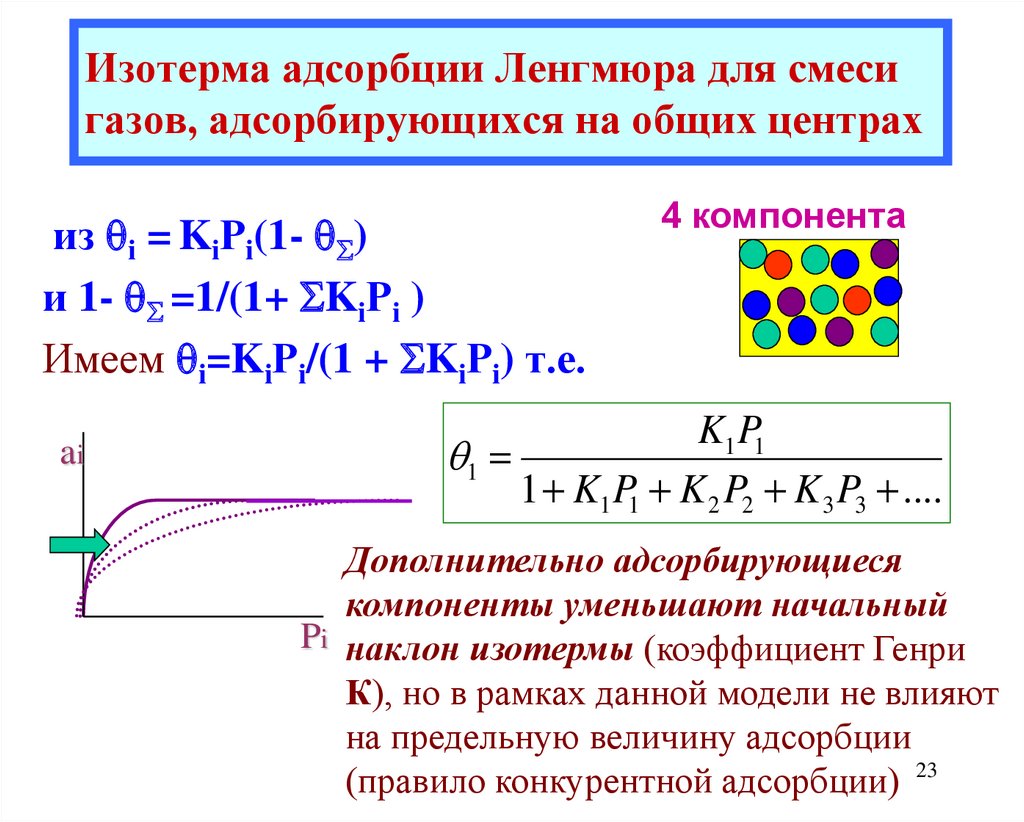
22. Изотерма адсорбции Ленгмюра для смеси газов А и В, адсорбирующихся на общих центрах.
простейший квазихимический выводА + [Z] [AZ] константа скорости
РА (1- )
А
KA= А/ РА(1- );
B + [Z] [BZ]
РB (1- )
B
KB= B/ РB(1- )
i = KiРi(1 - )
= i = KiРi(1 - ) = (1- ) KiРi
доля занятой поверхности = KiРi/(1+ KiРi )
1- =1/(1+ KiРi )
22
23. Изотерма адсорбции Ленгмюра для смеси газов, адсорбирующихся на общих центрах
из i = KiРi(1- )и 1- =1/(1+ KiРi )
Имеем i=KiРi/(1 + KiРi) т.е.
ai
4 компонента
K1 P1
1
1 K1 P1 K 2 P2 K 3 P3 ....
Дополнительно адсорбирующиеся
компоненты уменьшают начальный
Pi наклон изотермы (коэффициент Генри
К), но в рамках данной модели не влияют
на предельную величину адсорбции
(правило конкурентной адсорбции) 23
24. Изотерма Ленгмюра для адсорбции с диссоциацией молекулы на два фрагмента
При равновесии по схеме А2 + 2 [Z] 2[AZ]адсорбция А2 в виде 2А требует наличия пары
свободных центров, число свободных пар
пропорционально (1- A)2 ,
для десорбции требуется два соседних атома на
поверхности, число таких пар пропорционально A2,
константа равновесия
K = А2/(1- А)2PА
В результате
А = (КPA)1/2 /[1 + (КPA)1/2]
24
25. Модельный пример: адсорбция О3
Молекулярная (О3):= КР/( 1 + КР)
Диссоциативная (О2 + О)
= КР1/2/( 1 + КР1/2)
Диссоциативная (О + О + О)
= КР1/3/( 1 + КР1/3)
25
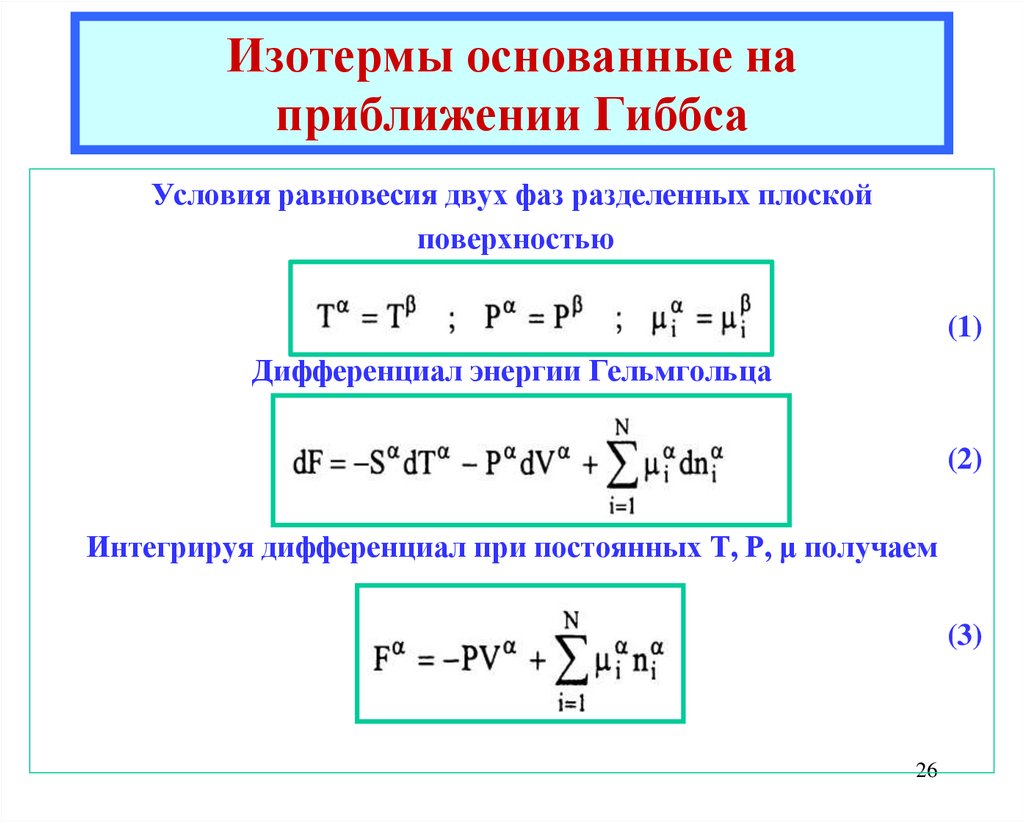
26. Изотермы основанные на приближении Гиббса
Условия равновесия двух фаз разделенных плоскойповерхностью
(1)
Дифференциал энергии Гельмгольца
(2)
Интегрируя дифференциал при постоянных T, P, μ получаем
(3)
26
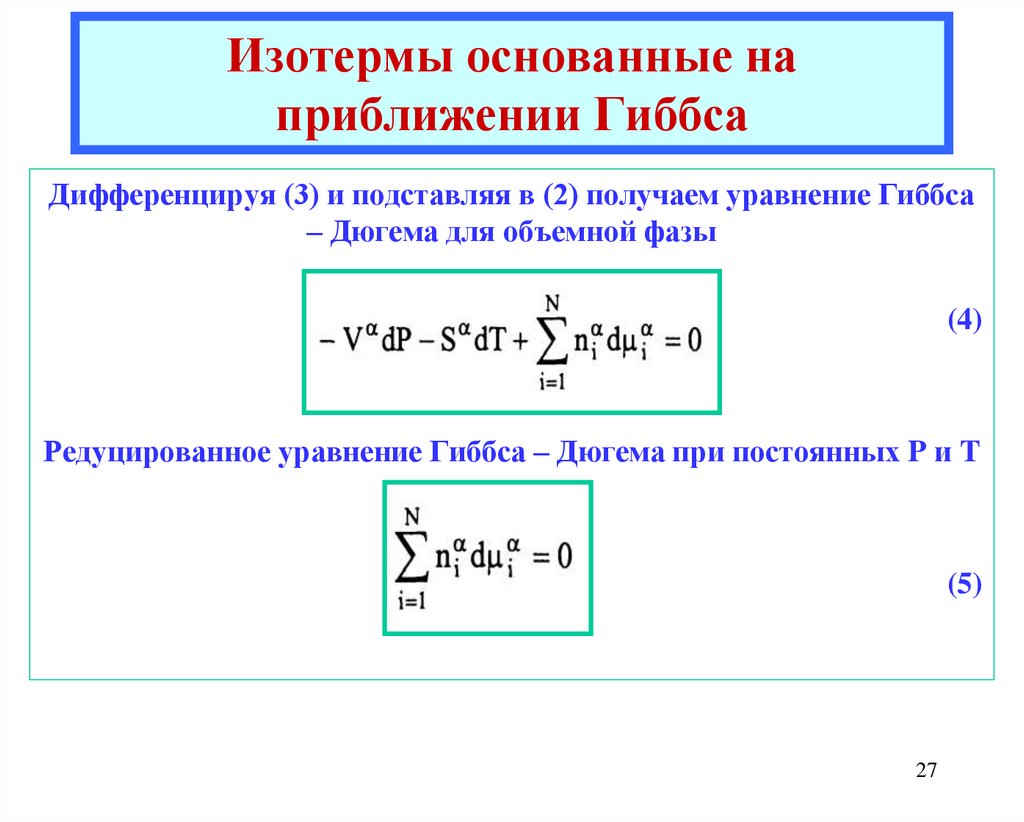
27. Изотермы основанные на приближении Гиббса
Дифференцируя (3) и подставляя в (2) получаем уравнение Гиббса– Дюгема для объемной фазы
(4)
Редуцированное уравнение Гиббса – Дюгема при постоянных P и T
(5)
27
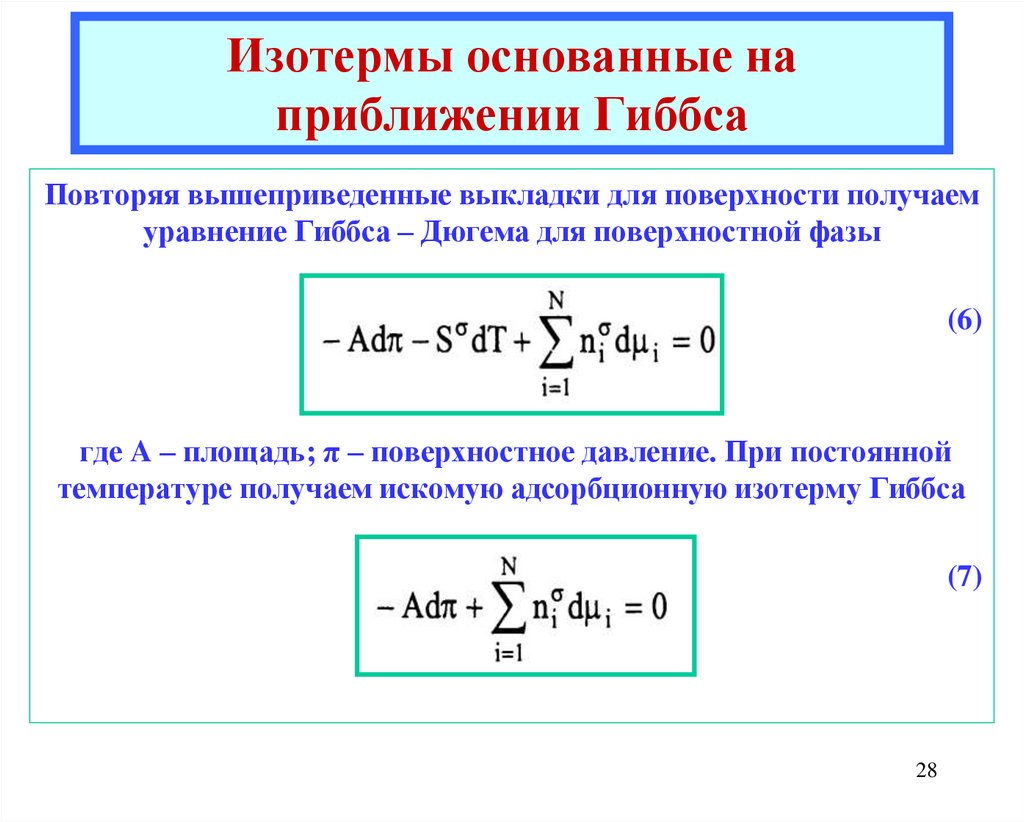
28. Изотермы основанные на приближении Гиббса
Повторяя вышеприведенные выкладки для поверхности получаемуравнение Гиббса – Дюгема для поверхностной фазы
(6)
где A – площадь; π – поверхностное давление. При постоянной
температуре получаем искомую адсорбционную изотерму Гиббса
(7)
28
29. Изотермы основанные на приближении Гиббса
Для однокомпонентной адсорбции уравнение изотермы принимаетследующий вид
(8)
Используя условия равновесия (1) между поверхностью и газовой
фазой можно записать (считая газ идеальным)
(9)
Из (8), (9) получаем следующее уравнение адсорбционной изотермы
Гиббса
(10)
29
30. Изотермы основанные на приближении Гиббса
Линейная изотерма (закон Генри)Для однородной поверхности в области предельно малого
заполнения уравнение состояния поверхности тождественно
уравнению состояния идеального газа
(11)
Подставляя (11) в (10) получаем
Из (11), (12) следует
(12)
- закон Генри, где K(T) –
постоянная Генри
31. Область малых заполнений - изотерма адсорбции Генри (кинетический подход)
число ударов n = NAP/(2 MRT)1/2/см2суравнение изотермы:
Г
Р
при Т= Const
Г = n ( е Q/RT) = Кг P
0
Г – среднее число молекул на единице
поверхности , Кг – коэффициент Генри,
- коэффициент прилипания.
В этой области межмолекулярное взаимодействие
адсорбат/адсорбат (G/G) пренебрежимо мало и определяющим
является взаимодействие адсорбат/адсорбент (G/H).
Адсорбционные измерения в области Генри используют для
определений взаимодействия G/H. Уравнение Генри – предельная
форма всех «правильных»изотерм адсорбции при Р 0 или =
Г/Гмах 0,
31
32. Изотермы основанные на приближении Гиббса
Изотерма ФольмераУравнение состояния поверхностного газа с учетом размера частиц
для делокализованной адсорбции
(13)
Повторяя выкладки предыдущих слайдов получаем уравнение
Фольмера
(14)
Уравнение (13) является точным уравнением для системы жестких стержней на
прямой (уравнение Тонкса). Соответственно уравнение Фольмера является точным
для этого случая.
33. Изотермы основанные на приближении Гиббса
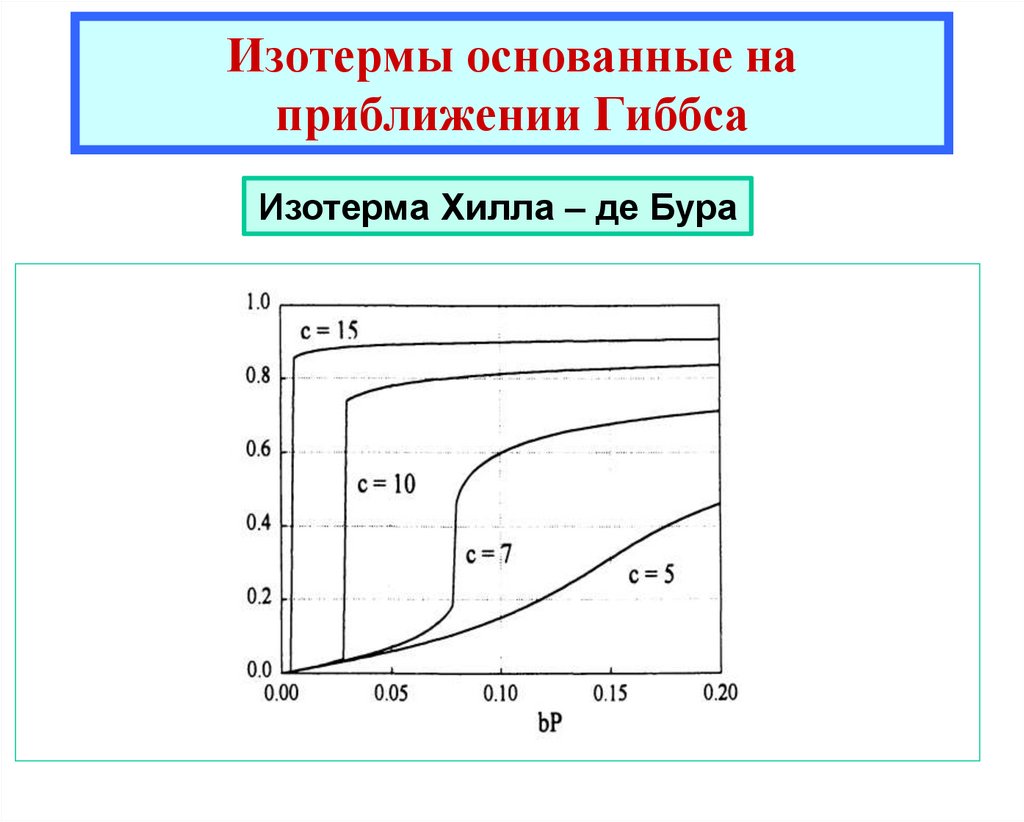
Изотерма Хилла – де БураЕсли в качестве уравнения состояния поверхностного газа взять
уравнение Ван-дер-Ваальса
(15)
то получаем уравнение Хилла-де-Бура
(16)
Уравнение (16) описывает делокализованную адсорбцию с учетом жесткой
сердцевины и притяжения ближайших соседей.
34. Изотермы основанные на приближении Гиббса
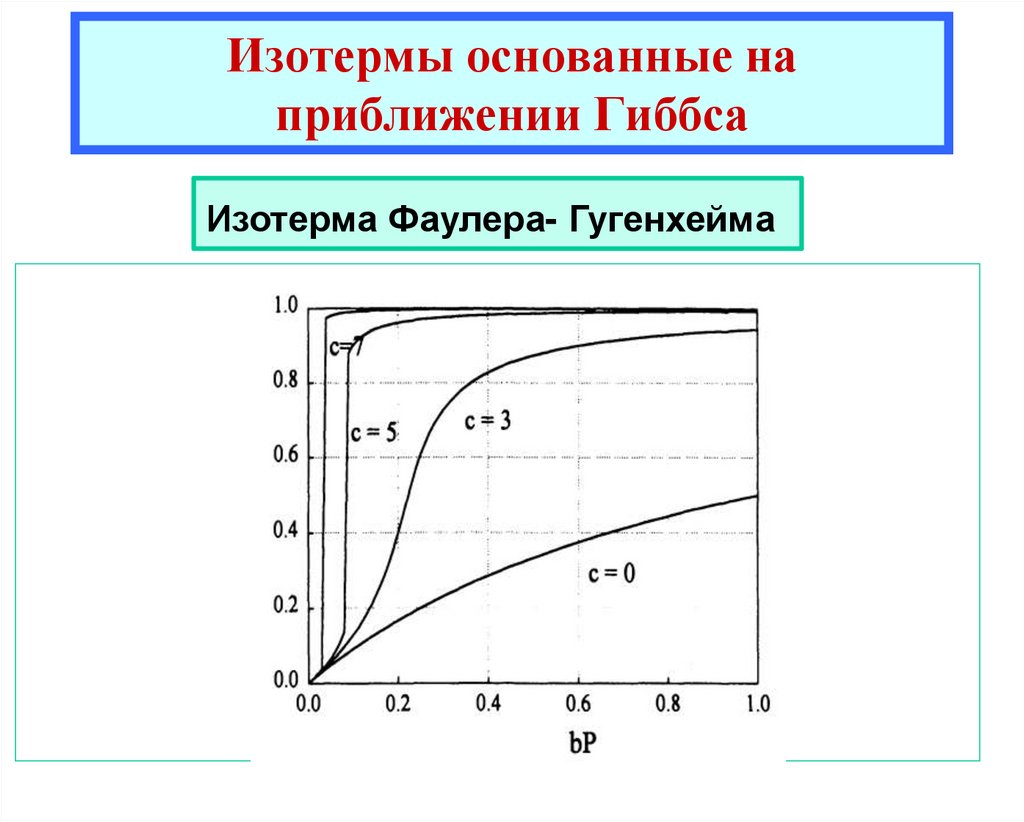
Изотерма Фаулера- ГугенхеймаЕсли вместо делокализованной адсорбции рассмотреть
локализованную то из уравнения Хилла-де-Бура мы получим
уравнение Фаулера - Гугенхейма
(17)
Уравнение (17) описывает локализованную адсорбцию с учетом взаимодействия
ближайших соседей.
35. Изотермы основанные на приближении Гиббса
Изотерма Фаулера- Гугенхейма36. Изотермы основанные на приближении Гиббса
Изотерма Хилла – де Бура37. Изотермы основанные на приближении Гиббса
38. Метод БЭТ
Полимолекулярная адсорбцияМетод БЭТ
Stephen Brunauer,
Pаule H. Emmett
Edward Teller
J. Amer. Chem. Soc. 60, 2309, 1938.
Стефан Брунауэр, Адсорбция газов и паров
М., ИЛ, 1948 г (амер. издание 1945) 781 стр
• Редактор русск перевода акад М.М. Дубинин
38
39. Уравнение БЭТ (Брунауэр-Эмметт-Теллер)
Уравнение БЭТ (БрунауэрЭмметт-Теллер)полимолекулярная
адсорбция по БЭТ
монослой
Ленгмюра
Модель БЭТ рассматривает адсорбцию
на однородной поверхности как серию
квазихимических реакций образования
комплексов из одной, двух и т.д. молекул
(в виде вертикальных столбиков):
G + свободная поверхность H [единичные комплексы G/H]
G + комплекс G/H [двойной комплекс G2/H]
G + комплекс G2/H [тройной комплекс G3/H] и т.д.
без учета взаимодействия между комплексами
39
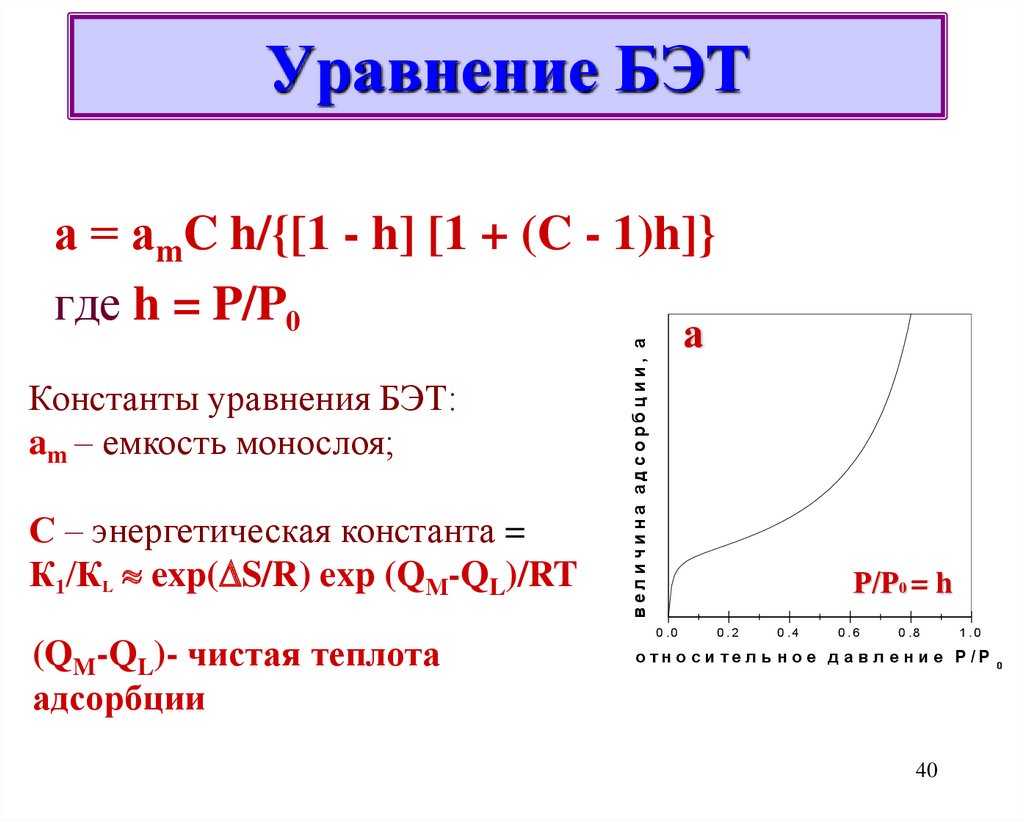
40. Уравнение БЭТ
а = аmC h/{[1 - h] [1 + (C - 1)h]}где h = P/P0
С – энергетическая константа =
К1/КL exp( S/R) exp (QМ-QL)/RT
(QM-QL)- чистая теплота
адсорбции
величина адсорбции, а
Константы уравнения БЭТ:
am – емкость монослоя;
а
Р/Р0 = h
0 .0
0 .2
0 .4
0 .6
0 .8
1 .0
о тн о с и те л ь н о е д а в л е н и е Р /Р
40
0
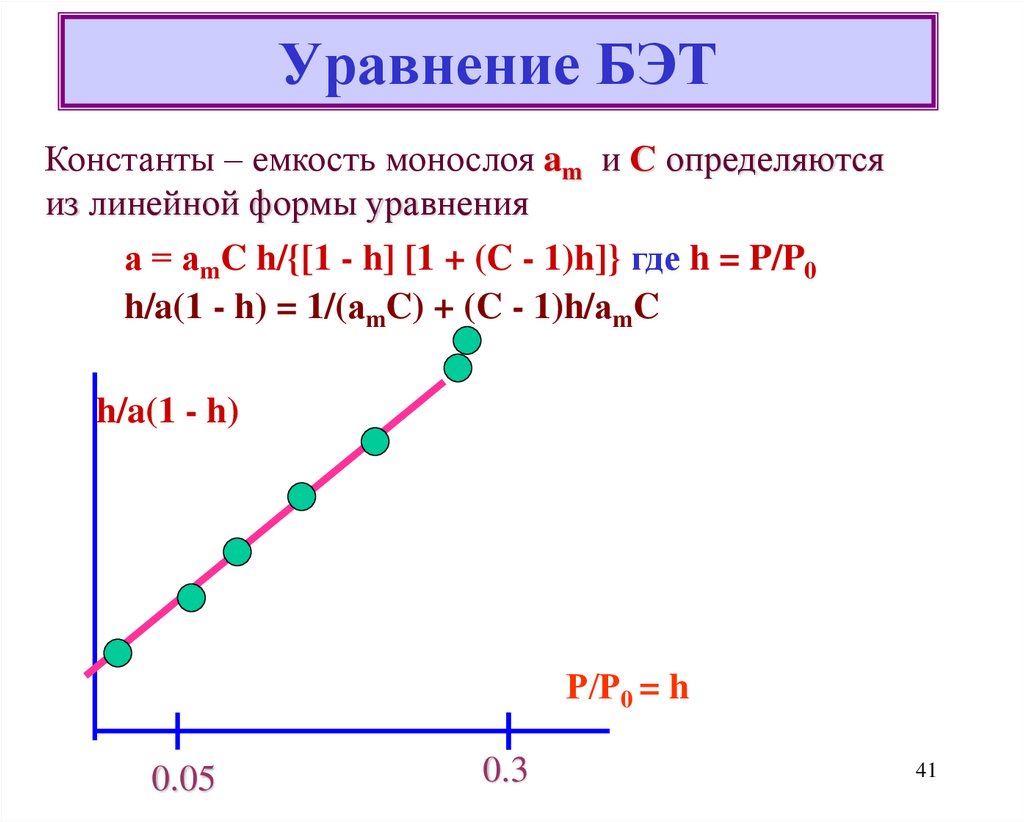
41. Уравнение БЭТ
Константы – емкость монослоя am и С определяютсяиз линейной формы уравнения
а = аmC h/{[1 - h] [1 + (C - 1)h]} где h = P/P0
h/a(1 - h) = 1/(аmC) + (C - 1)h/аmC
h/a(1 - h)
Р/Р0 = h
0.05
0.3
41
42. Уравнение БЭТ
Величину am (мМоль/г) используют длярасчета удельной поверхности А
А = аm NA
где NA - число Авогадро,
- площадка, приходящаяся на одну
молекулу в заполненном монослое на
поверхности адсорбента.
=АПР/(1- S)
Апр –площадь проекции молекулы
на плоскость.
42
43. Молекулярные площадки в монослое
Молекулярные площадки в монослоеДля расчета Брунауэр и Эмметт предложили уравнение
сф = 1.091(М/NA ) 2/3
которое получено при допущении сферической формы молекул G,
которые образуют плотнейшую упаковку на поверхности и в объеме.
Для стандартного в большинстве публикаций адсорбата - N2 при 77K
N2 = 0.162 нм2
Однако расчеты для других адсорбатов обычно дают несогласованные
значения АiБЭТ
АiБЭТ AN2БЭТ
Поэтому для других адсорбатов на практике используют «приведенные»
значения i. Для выполнения условия А = Const
amN2NA N2 = amINA i = А,,откуда
i = N2 (amN2/ami)
В литературе предложены таблицы рекомендуемых значений i
для многих адсорбатов.
43
44. Метод БЭТ
Стандартные измерения – N2, 77 K,= 0.162 нм2
N2
Но применение метода БЭТ может быть
корректным при полном отсутствии
микропор и химических модификаторов
поверхности при щупа = Const
44
45. Метод БЭТ
4546.
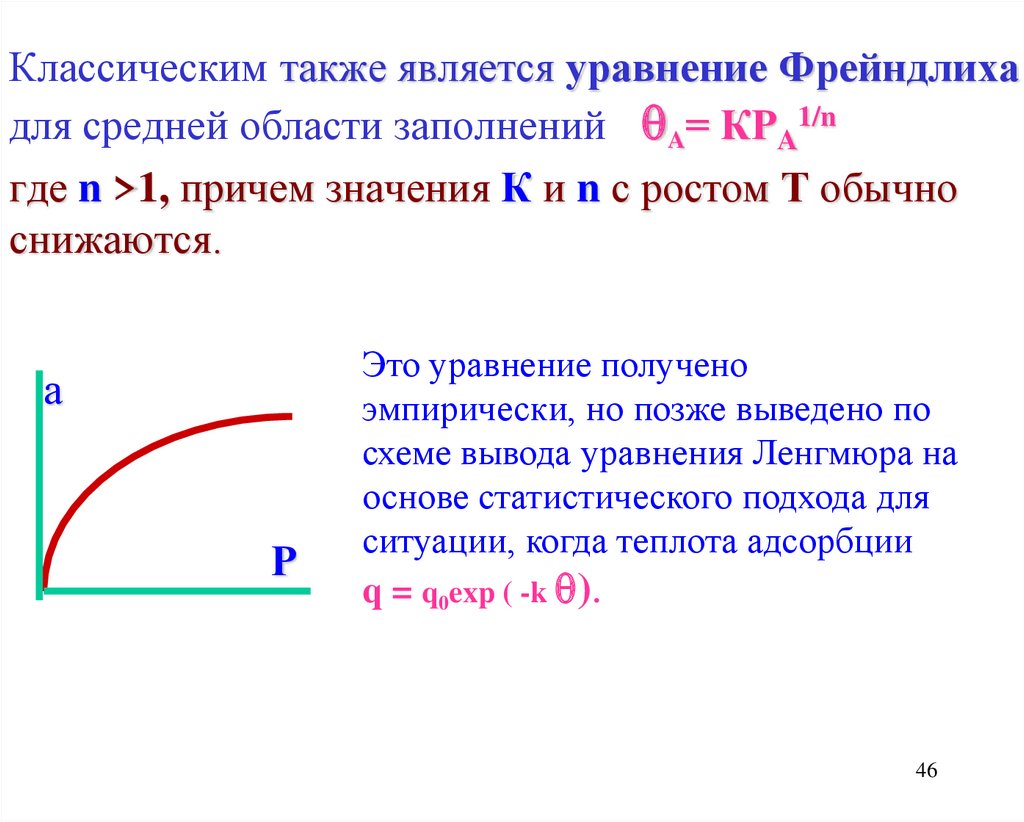
Классическим также является уравнение Фрейндлихадля средней области заполнений A= КPA1/n
где n >1, причем значения К и n с ростом Т обычно
снижаются.
а
Р
Это уравнение получено
эмпирически, но позже выведено по
схеме вывода уравнения Ленгмюра на
основе статистического подхода для
ситуации, когда теплота адсорбции
q = q0exp ( -k ).
46
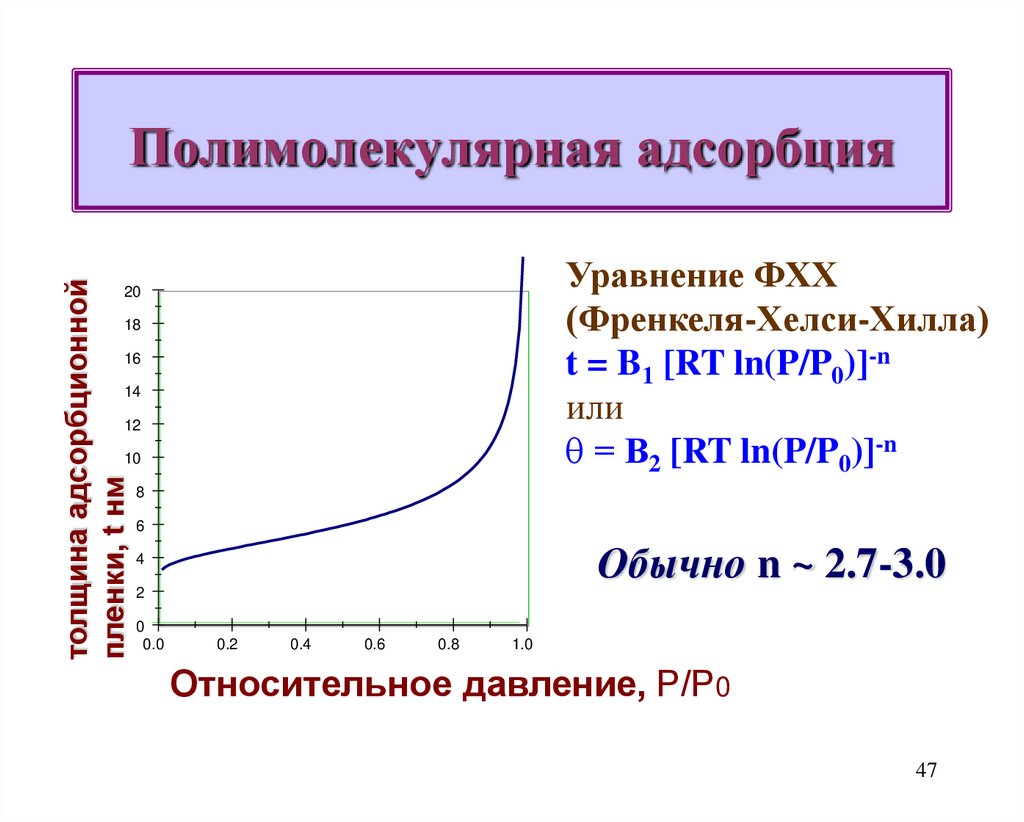
47. Полимолекулярная адсорбция
толщина адсорбционнойпленки, t нм
Полимолекулярная адсорбция
Уравнение ФХХ
(Френкеля-Хелси-Хилла)
t = B1 [RT ln(P/P0)]-n
или
= В2 [RT ln(P/P0)]-n
20
18
16
14
12
10
8
6
Обычно n ~ 2.7-3.0
4
2
0
0.0
0.2
0.4
0.6
0.8
1.0
Относительное давление, Р/Р0
47




























 Химия
Химия








