Геометрическая кристаллография

1. Раздел 1. Геометрическая кристаллография

Основные понятия кристаллографии
Элементы симметрии континуума
и теоремы их сложения
Классы симметрии (точечные группы)
Элементы симметрии дисконтинуума.
Системы трансляций Бравэ. Базис.
Пространственные группы,
правильные системы точек
1

2. Лекция 1.1. Основные понятия кристаллографии

Понятие о кристалле
Пространственная решетка
Элементарная ячейка
Категории и сингонии
Индексы плоскостей и направлений
кристалла
Проекции кристаллов
2

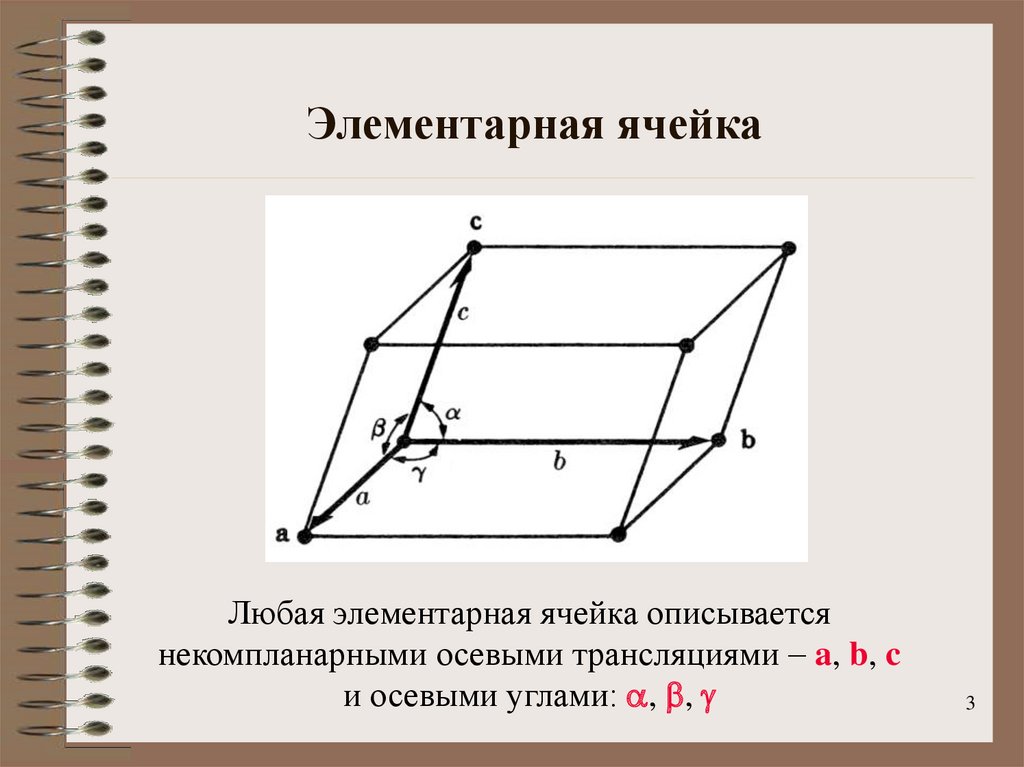
3. Элементарная ячейка

Любая элементарная ячейка описывается
некомпланарными осевыми трансляциями - a, b, c
и осевыми углами: a, b, g
3

4. Правила выбора элементарной ячейки

элементарная ячейка должна лучшим образом
отражать симметрию решетки;
предпочтение отдается перпендикулярным
и равным друг другу трансляциям, т.е.
число прямых углов и одинаковых
трансляций должно быть максимальным;
объем ячейки должен быть минимальным.
4

5. Разделение кристаллов на сингонии и категории

Сингония
Оси координат
триклинная
a ≠b ≠ c
a ≠ b ≠ g ≠ 90
a≠b≠c
a = g = 90 , b ≠ 90
a≠b≠c
a = b = g = 90
a=b=c
a = b = g ≠ 90
a=b≠c
a = b = g = 90
a=b≠c
a = b = 90 , g = 120
a=b=c
a = b = g = 90
моноклинная
ромбическая
тригональная
тетрагональная
гексагональная
кубическая
Категория
низшая
средняя
высшая
5

6. Индексы плоскостей и направлений кристалла

[[m, p, q]] координаты узла
индексы направления - три целых,
взаимно простых числа, пропорциональных
координатам любой точки, лежащей на
этом направлении, если оно проходит через
начало координат
[uvw]
[uvw]
z
y
x
(hkl)
z
(hkl)
y
x
индексы плоскости – три целых, взаимно
простых числа, обратно пропорциональных
отрезкам, отсекаемым этой плоскостью на
осях координат
6

7. Межплоскостное расстояние

z
d(hkl)
n(hkl)
(hkl)
y
x
(hkl) – семейство параллельных плоскостей
d(hkl) – межплоскостное расстояние
7

8. Совокупность плоскостей

1
2
d гекс
1
2
d куб
4(h 2 hk k 2 ) l 2
2
2
3a
c
h 2 k 2 l2
a2
1
d 2ромбич
1
d 2тетр
h 2 k 2 l2
2 2 2
a
b
c
h 2 k 2 l2
2
2
a
c
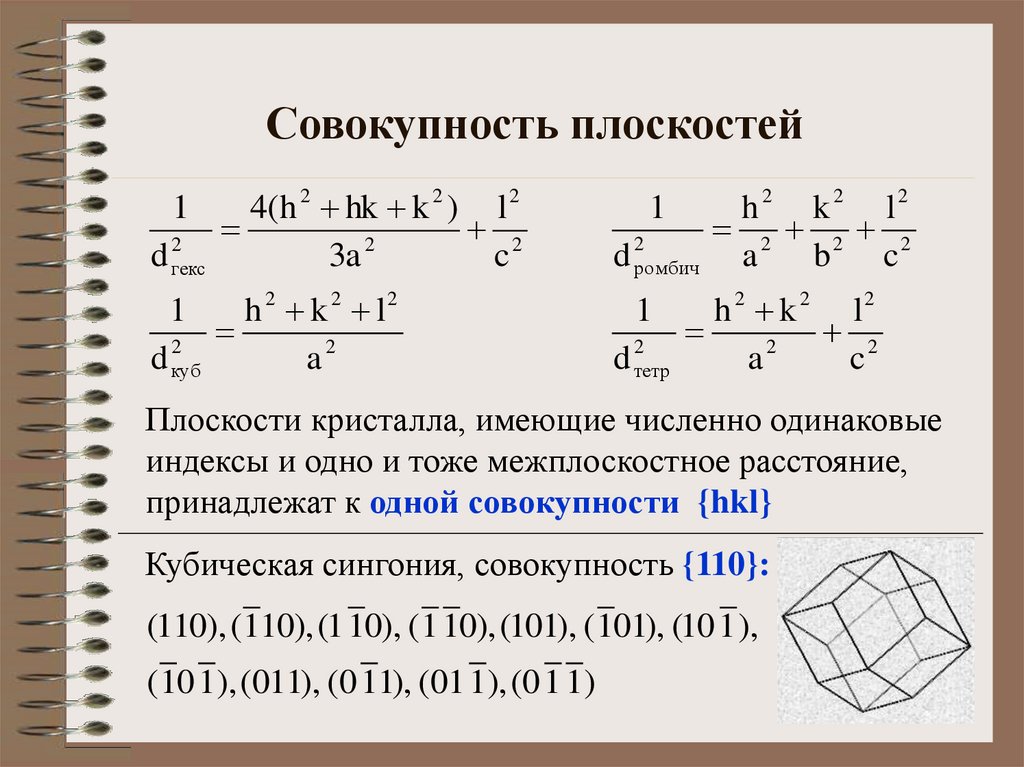
Плоскости кристалла, имеющие численно одинаковые
индексы и одно и тоже межплоскостное расстояние,
принадлежат к одной совокупности {hkl}
Кубическая сингония, совокупность {110}:
(110),(110),(1 10), (1 10),(101), (101), (10 1),
(10 1),(011), (0 11), (01 1),(0 1 1)
8

9. Зона плоскостей

Плоскости кристалла, параллельные одному общему
направлению, образуют зону плоскостей, а это общее
направление называется осью зоны.
Условие зональности:
hu + kv + lw = 0,
т.е. плоскость (hkl)
принадлежит зоне с
осью [uvw]
9

10. Лекция 1.2. Элементы симметрии континуума и теоремы их сложения

Элементы симметрии континуума
Эпюры элементов симметрии
Теоремы сложения элементов симметрии
Определяющие элементы симметрии
Установка кристалла
10

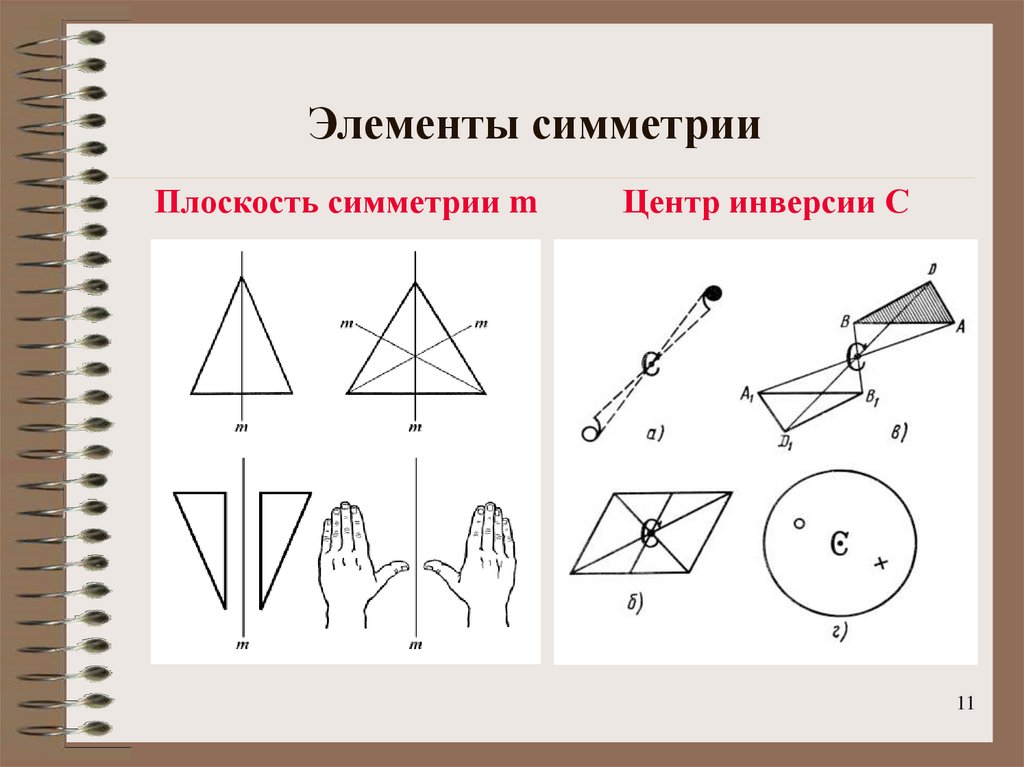
11. Элементы симметрии

Плоскость симметрии m
Центр инверсии С
11

12. Элементы симметрии

Плоские фигуры с осями симметрии
разного порядка
2-го порядка
3-го порядка
4-го порядка
5-го порядка
6-го порядка
12

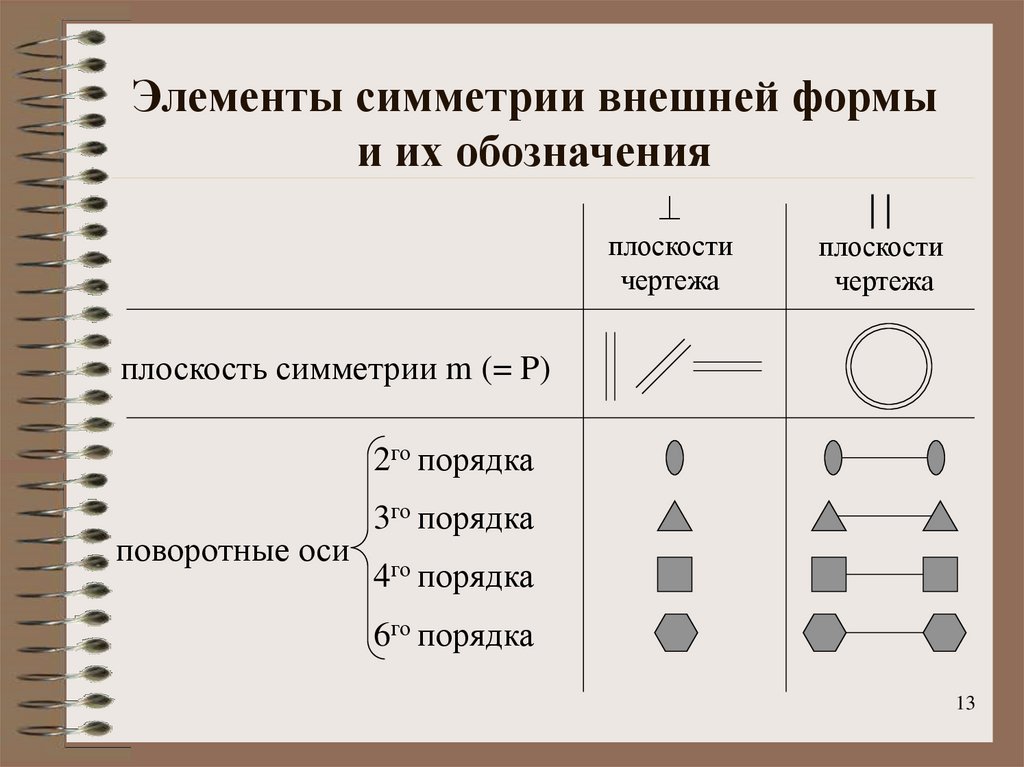
13. Элементы симметрии внешней формы и их обозначения

||
плоскости
чертежа
плоскости
чертежа
плоскость симметрии m (= P)
2го порядка
поворотные оси
3го порядка
4го порядка
6го порядка
13

14. Элементы симметрии внешней формы и их обозначения

||
плоскости
чертежа
плоскости
чертежа
центр симметрии 1 ( C )
3го порядка
инверсионные
оси
4го порядка
6го порядка
14

15. Иллюстрация равенства

m 2
15

16. Теоремы сложения элементов симметрии

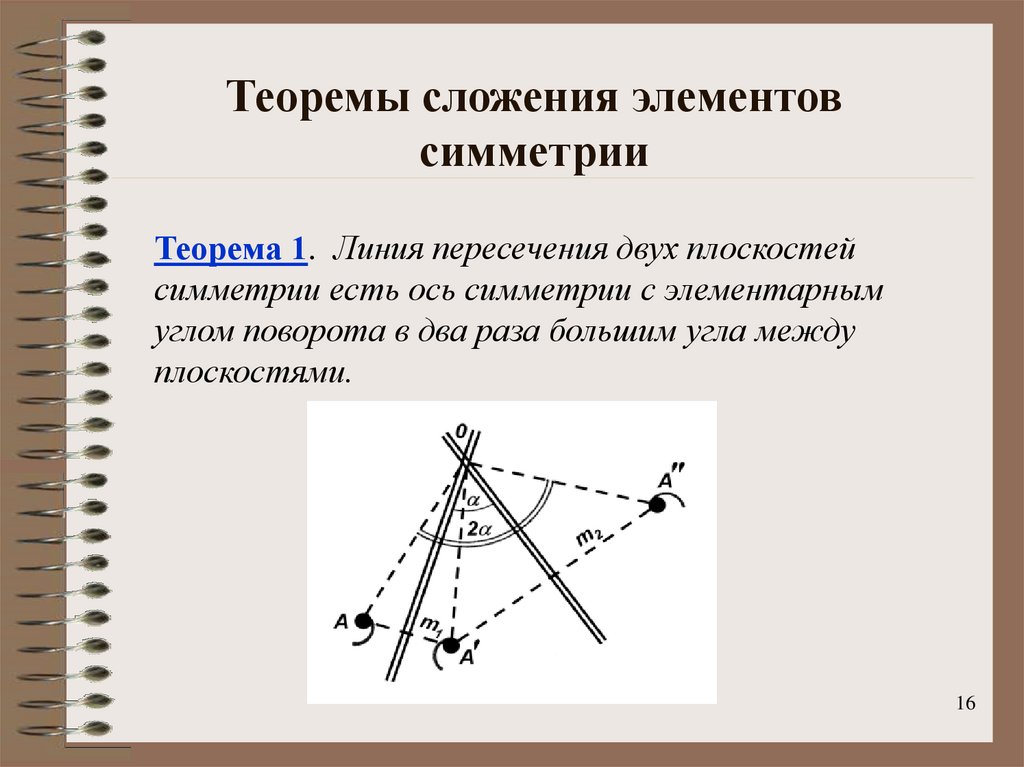
Теорема 1. Линия пересечения двух плоскостей
симметрии есть ось симметрии с элементарным
углом поворота в два раза большим угла между
плоскостями.
16

17. Теоремы сложения элементов симметрии

Теорема 2. Через точку пересечения двух осей
симметрии проходит третья, равнодействующая им.
Теорема 3. В точке пересечения оси четного порядка
с перпендикулярной ей плоскостью симметрии
расположен центр инверсии.
Cледствие:
В центросимметричном кристалле сумма осей
симметрии четного порядка равна числу плоскостей
симметрии.
17

18. Теоремы сложения элементов симметрии

Теорема 4. Если перпендикулярно оси порядка n
расположена хотя бы одна ось второго порядка,
то число таких осей второго порядка равно n.
18

19. Теоремы сложения элементов симметрии

Теорема 5. Если через ось порядка n проходит хотя
бы одна плоскость симметрии, то всего таких
плоскостей симметрии должно быть n.
19

20. Характерная симметрия и установка кристалла в зависимости от сингонии

низшая категория
Характерная симметрия и установка
кристалла в зависимости от сингонии
Сингония
Характерная
симметрия
Расположение осей
триклинная
1 или 1
по ребрам кристалла
моноклинная
2 или 2 ( m)
осьY 2 или m
ромбическая
три оси 2 или
три оси 2 ( m)
оси X , Y , Z 2 или m
20

21. Характерная симметрия и установка кристалла в зависимости от сингонии

высшая средняя категория
Сингония
Характерная
симметрия
тригональная
ось 3 или 3
тетрагональная
ось 4 или 4
гексагональная
ось 6 или 6
кубическая
четыре оси 3
Расположение осей
главная ось
параллельна Z,
остальные – в
плоскости XY
оси X , Y , Z трем
осям 4, 4 или 2
21

22. Лекция 1.3. Классы симметрии (точечные группы)

Классы симметрии (точечные группы)
Главные направления
Общее и частное положения
22

23. Классы симметрии

Класс симметрии – множество элементов симметрии,
действующих на плоскости и направления в кристалле.
Вывод классов симметрии – перебор всех возможных
сочетаний элементов симметрии, пересекающихся
в одной точке.
Возможные варианты:
1) Классы с одной поворотной осью
2) Классы с одной инверсионной осью
3) Классы с 1ой поворотной осью и осями 2го порядка
4) Классы с одной поворотной осью и плоскостью
5) Классы с несколькими осями высшего порядка 23

24. Пример вывода классов симметрии

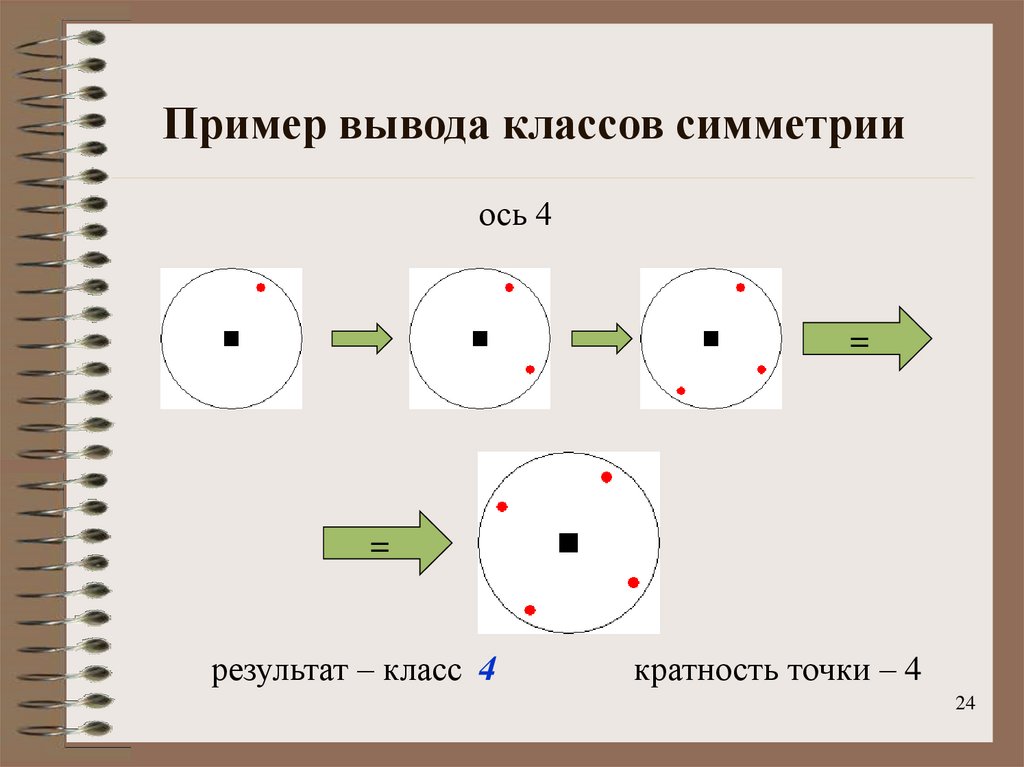
ось 4
=
=
результат – класс 4
кратность точки – 4
24

25. Пример вывода классов симметрии

ось 4 + 1
=
=
результат – класс 4/m
кратность точки – 8
25

26. Пример вывода классов симметрии

ось 4 + m
=
=
результат – класс 4/m
кратность точки – 8
26

27. Пример вывода классов симметрии

ось 4 + || m
=
результат – класс 4mm
кратность точки – 8
27

28. Пример вывода классов симметрии

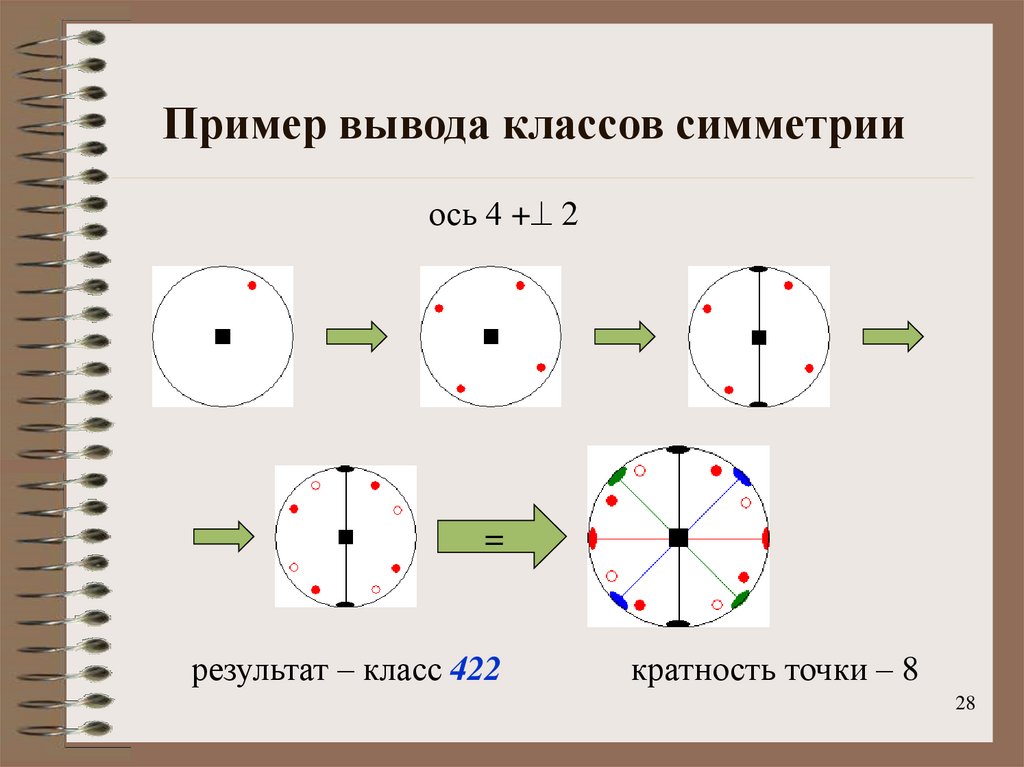
ось 4 + 2
=
результат – класс 422
кратность точки – 8
28

29. Пример вывода классов симметрии

ось 4 + || m + 1
или ось 4 + 2 + 1
=
результат – класс 4/m 2/m 2/m
кратность точки – 16
29

30. Главные направления

сингония
вектора
индексы
моноклинная
b
[010]
ромбическая
c, b, a
[001], [010], [100]
тригональная
c, b, a – b
[001], [010], [110]
тетрагональная
c, b, a – b
[001], [010], [110]
гексагональная
c, b, a – b
[001], [010], [110]
c, a + b + c, a – b
[001], [111], [110]
кубическая
30

31. Лекция 1.4. Элементы симметрии дисконтинуума

Системы трансляций Бравэ
Элементы симметрии дисконтинуума
Базис
31

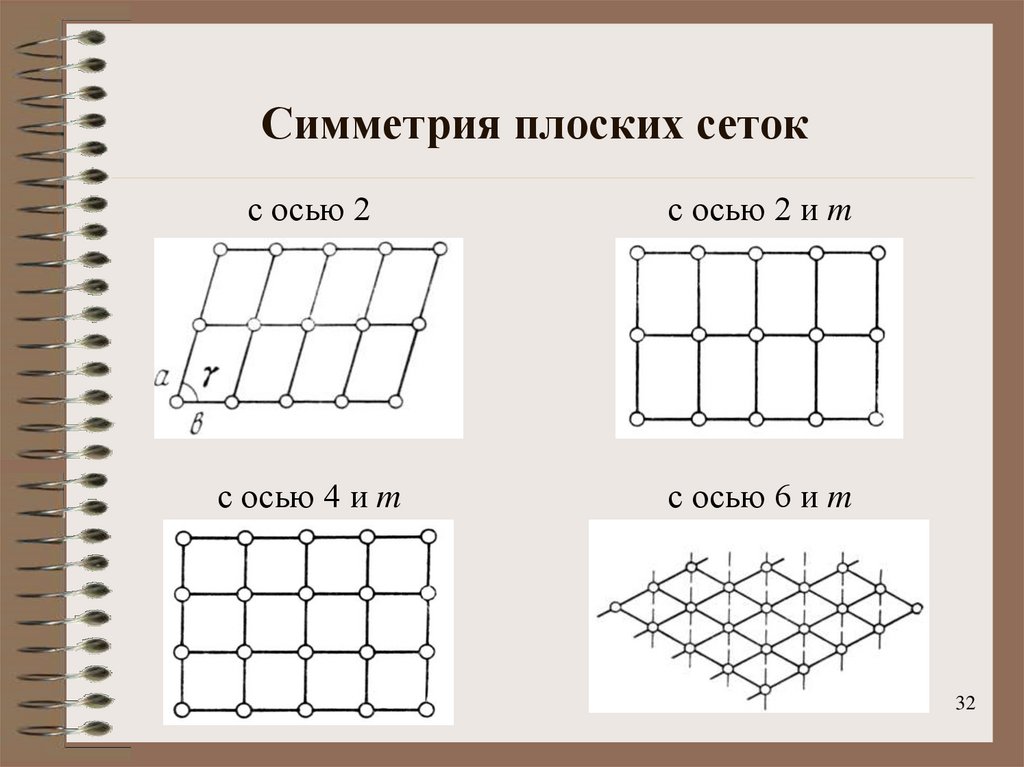
32. Симметрия плоских сеток

с осью 2
с осью 2 и m
с осью 4 и m
с осью 6 и m
32

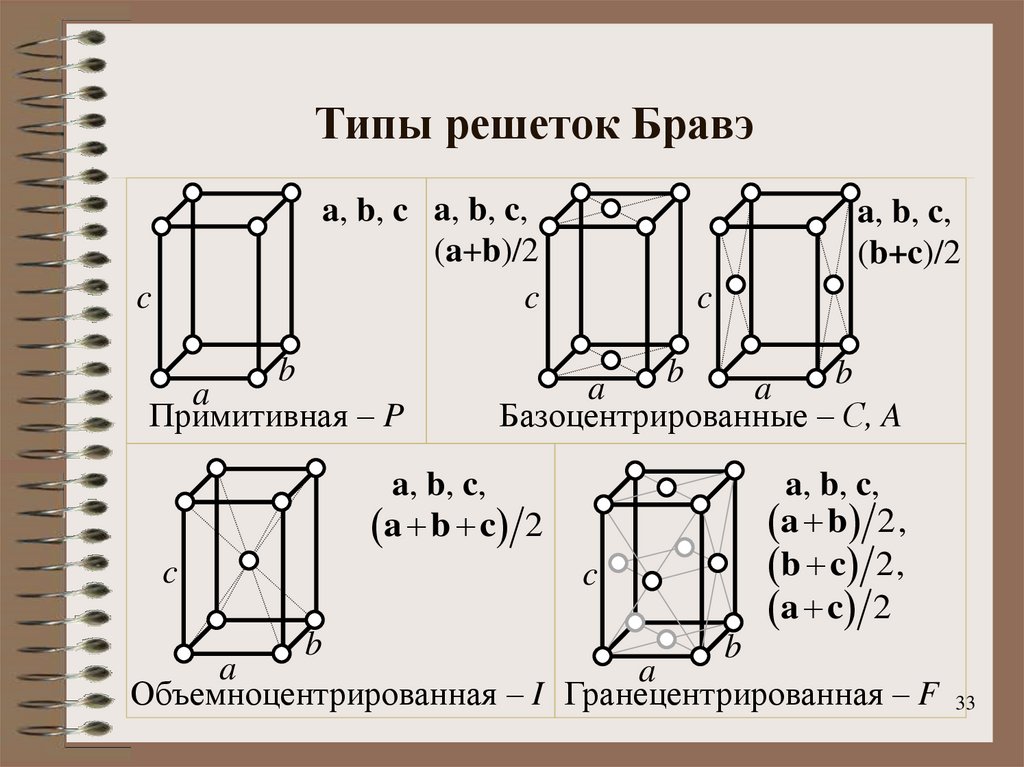
33. Типы решеток Бравэ

a, b, c a, b, c,
(a+b)/2
c
c
b
a
Примитивная – P
a, b, c,
(b+c)/2
c
b
b
a
a
Базоцентрированные – С, A
a, b, c,
a b c 2
c
c
a, b, c,
a b 2,
b c 2,
a c 2
b
b
a
a
Объемноцентрированная – I Гранецентрированная – F
33

34. Возможные решетки Бравэ в тетрагональной и кубической сингониях

Тетрагональная сингония
Кубическая сингония
34

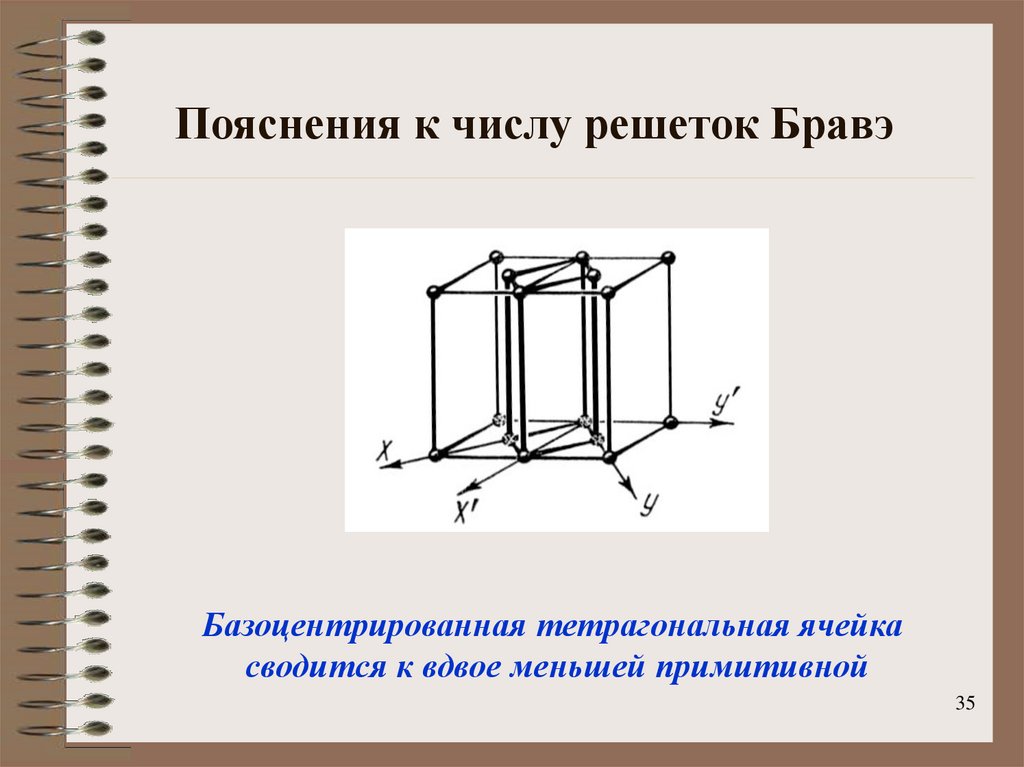
35. Пояснения к числу решеток Бравэ

Базоцентрированная тетрагональная ячейка
сводится к вдвое меньшей примитивной
35

36. Элементы симметрии дисконтинуума

Зеркальная плоскость симметрии m и
плоскость скользящего отражения a
36

37. Элементы симметрии дисконтинуума

t
t/4
ось 41
винтовая ось 41
37

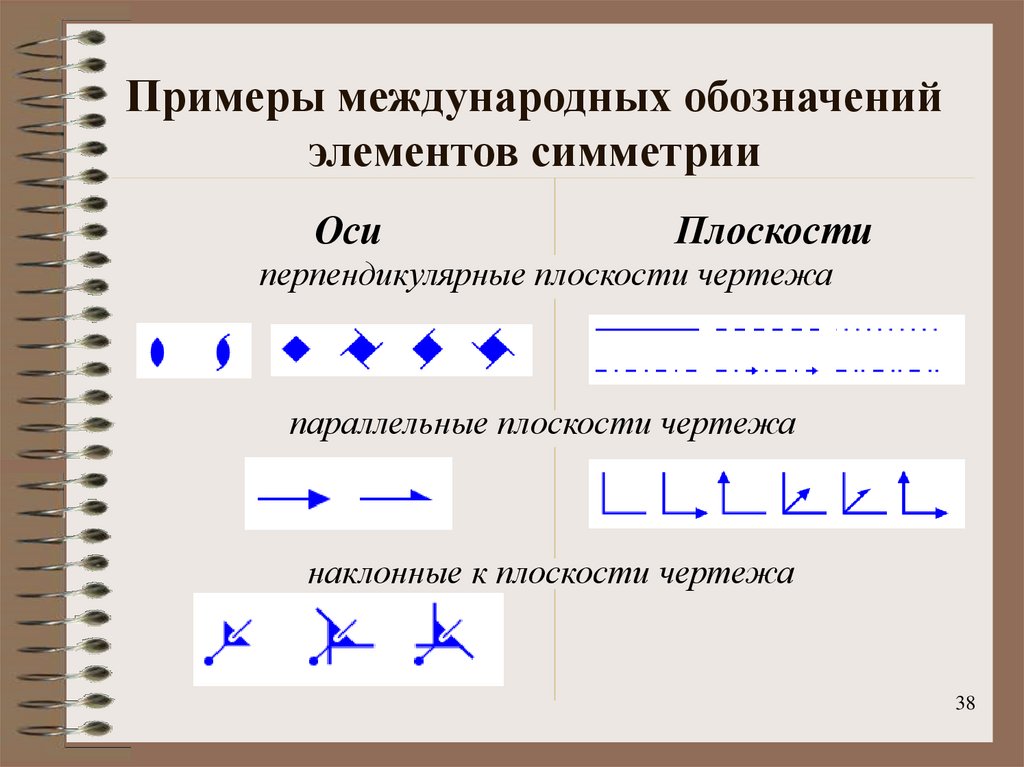
38. Примеры международных обозначений элементов симметрии

Оси
Плоскости
перпендикулярные плоскости чертежа
параллельные плоскости чертежа
наклонные к плоскости чертежа
38

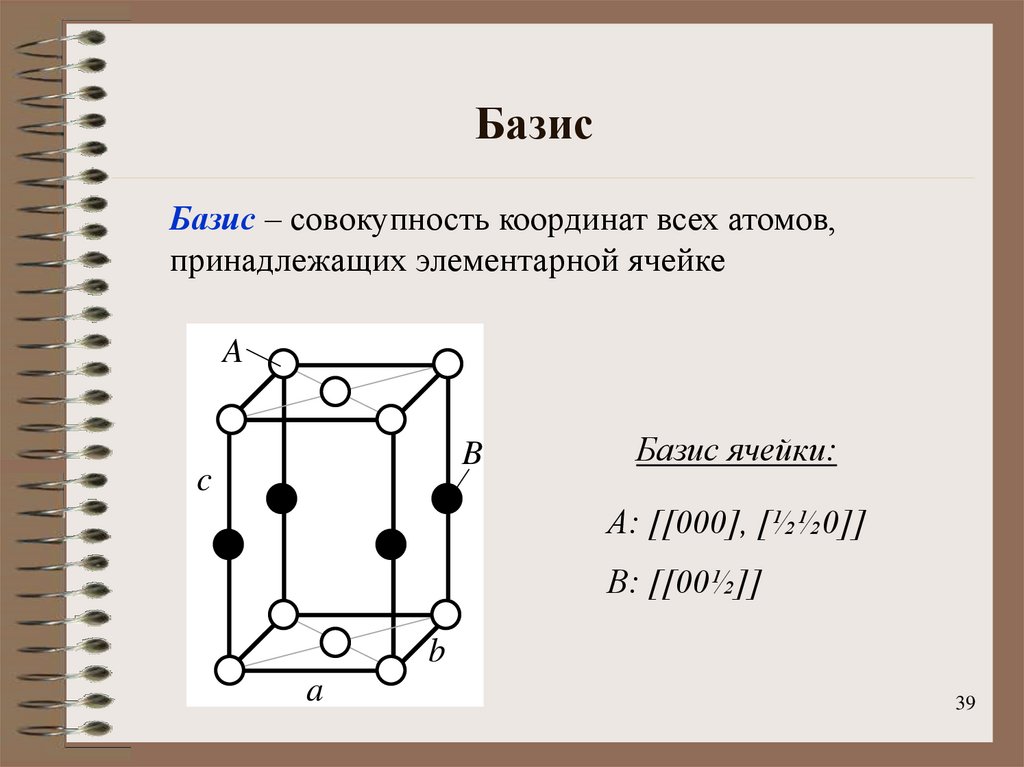
39. Базис

Базис – совокупность координат всех атомов,
принадлежащих элементарной ячейке
A
B
c
Базис ячейки:
A: [[000], [½½0]]
B: [[00½]]
b
a
39

40. Лекция 1.5. Пространственные группы

Пространственные группы
Правильные системы точек
40

41. Пространственная группа

Пространственная группа – совокупность элементов
симметрии, действующих на одну систему трансляций
(ячейку Бравэ).
4
2
F
3
m
m
I
II
III
IV
I – тип решетки Бравэ
II, III, IV – элементы симметрии в 1ом,
2ом и 3ем главных направлениях
41

42. Примеры пространственных групп

кубическая сингония
41 2
F 3
P23 P 43m
d m
тетрагональная сингония
41 2 2
4 2 2
I
I
a md
mmm
ромбическая сингония
P 222 Pnma Pmc21
гексагональная сингония
63 2 2
P
mmc
P6mm
P6
тригональная сингония
P32
P3m
моноклинная сингония
С2
P 21 m
42

43. Правильные системы точек

Правильная система точек (ПСТ) – совокупность
симметрично эквивалентных позиций (точек),
связанных преобразованиями пространственной группы
Обозначения для ПСТ:
2
(c) : ½ y 0
I
II
III
I – кратность позиции
II – тип позиции (по алфавиту из справочника)
III – координаты любого атома из ПСТ
43

44. ПСТ в группе P2/m

частное положение
b
a
z=0
z=0
z= 0
z= 0
z=0
Тип позиции:
z=0
1(a): 0 y 0
1(a): 0 y 0
44

45. ПСТ в группе P2/m

частное положение
b
a
z=½
z=½
z= 0
z= 0
z=½
Тип позиции:
z=½
1(b): 0 y ½
1(b): 0 y ½
45

46. ПСТ в группе P2/m

частное положение
b
z= 0
a
z=0
Тип позиции:
z= 0
1(с): ½ y 0
46

47. ПСТ в группе P2/m

частное положение
b
z= 0
a
z=½
Тип позиции:
z= 0
1(d): ½ y ½
47

48. ПСТ в группе P2/m

общее положение
b
z= 0
a
z= 0
Тип позиции:
Координаты точек:
2(e): x y z
xyz и xyz
48

49. Пример из Международных таблиц

49