Похожие презентации:
Планирование исследований
1. ПЛАНИРОВАНИЕ ИССЛЕДОВАНИЯ
2.
Экспериментальный план(экспериментальная схема)
Экспериментальный дизайн
(DESIGN)
3.
4.
• Проект конкретной последовательностиманипуляции со специально
сформированными группами называется
планом или дизайном (от англ. design —
проект, план, оформление)
исследования
(Александров, Максимова, 2001).
5. Классификации планов
6.
Экспериментальная выборкаКонтрольная выборка
7.
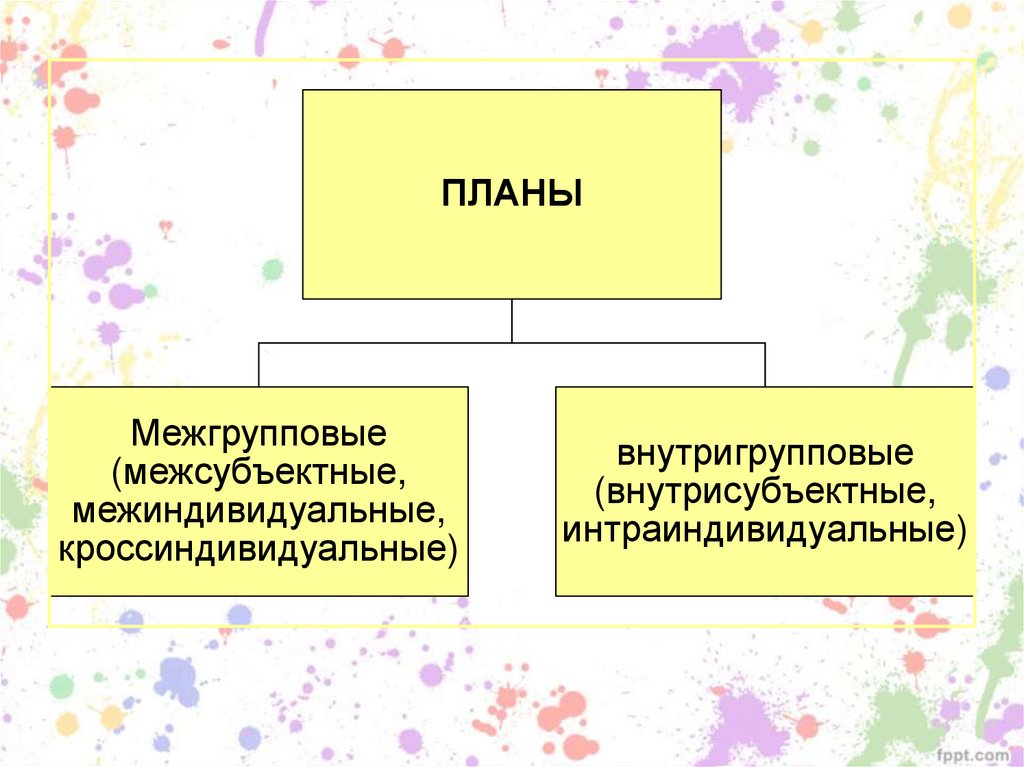
ПЛАНЫМежгрупповые
(межсубъектные,
межиндивидуальные,
кроссиндивидуальные)
внутригрупповые
(внутрисубъектные,
интраиндивидуальные)
8.
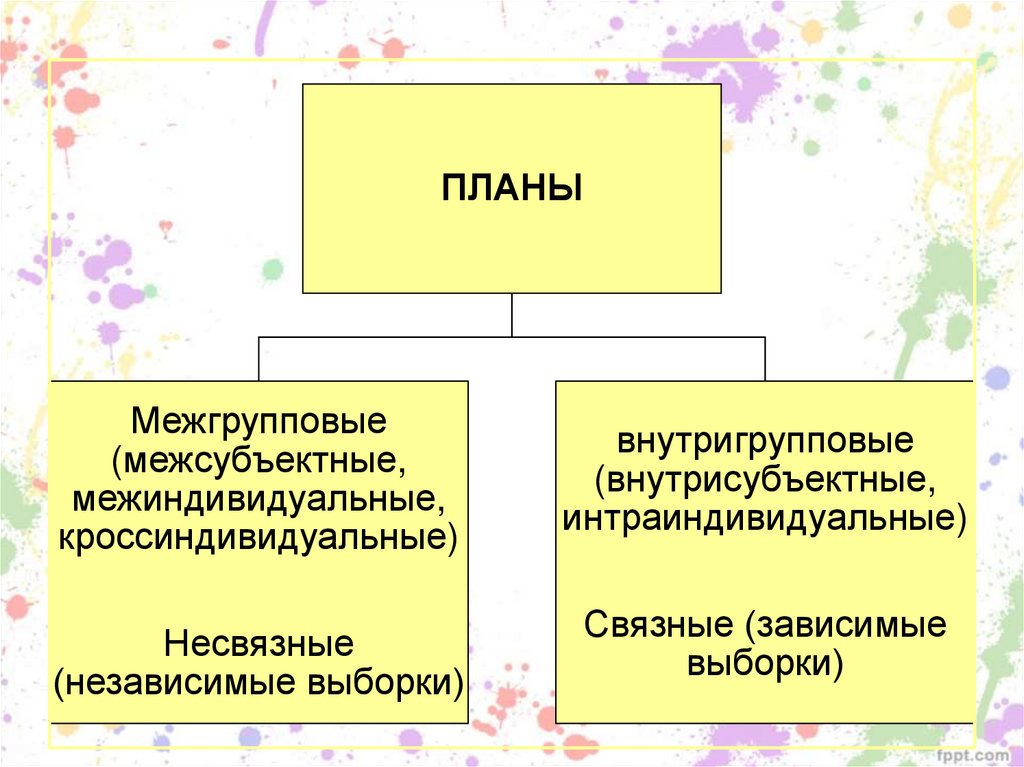
ПЛАНЫМежгрупповые
(межсубъектные,
межиндивидуальные,
кроссиндивидуальные)
Несвязные
(независимые выборки)
внутригрупповые
(внутрисубъектные,
интраиндивидуальные)
Связные (зависимые
выборки)
9.
ВНУТРИГРУППОВЫЕ ПЛАНЫ10.
• Внутригрупповые планы требуютменьших выборок
• Не применимы, если каждый уровень
условие занимает длительное время.
• Не применимы, если выполнение
одного условия несовместимо с
выполнением другого условия на одной
и той же выборке.
(например, нужно использовать один и тот же
стимульный материал и при одном и при другом
условии, а это делает задачу бессмысленной)
11.
• Контроль фактора времени вовнутригрупповых планах становится
отдельной проблемой, которая частично
может решаться переходом к
кроссиндивидуальному эксперименту –
к межгрупповым планам.
12.
• МЕЖГРУППОВЫЕ ПЛАНЫ13. Проблема создания эквивалентных групп
• Рандомизация• Уравнивание групп
14.
• разные экспериментальныеусловия
• уровни независимой переменной
• разные методики
• Разные пробы
15.
• Систематические смешения• Эффект последовательности или
эффект порядка.
16. Эффект прогрессии
•(выполнение заданий равномерно(прогрессивно) изменяется от
попытки к попытке).
17. эффект тренировки
• После первой попытки вторая попыткабудет выполнена лучше.
18.
повторение попыток постепенно приводитк усталости или скуке и задания
выполняются все хуже и хуже.
19.
• ЭФФЕКТ ВРАБАТЫВАНИЯ20. Эффект передачи
(одни последовательностизаданий могут приводить к
результату, отличному от того,
который вызывается другими
последовательностями заданий)
21. ПЕРЕНОС
ПОЛОЖИТЕЛЬНЫЙОТРИЦАТЕЛЬНЫЙ
СИММЕТРИЧНЫЙ
АСИММЕТРИЧНЫЙ
22.
• Кумулятивный эффект23.
• Однородные (постепенноеулучшение от пробе к пробе) и
неоднородные эффекты (чаще
случается так, что процесс научения
сначала протекает более интенсивно, а
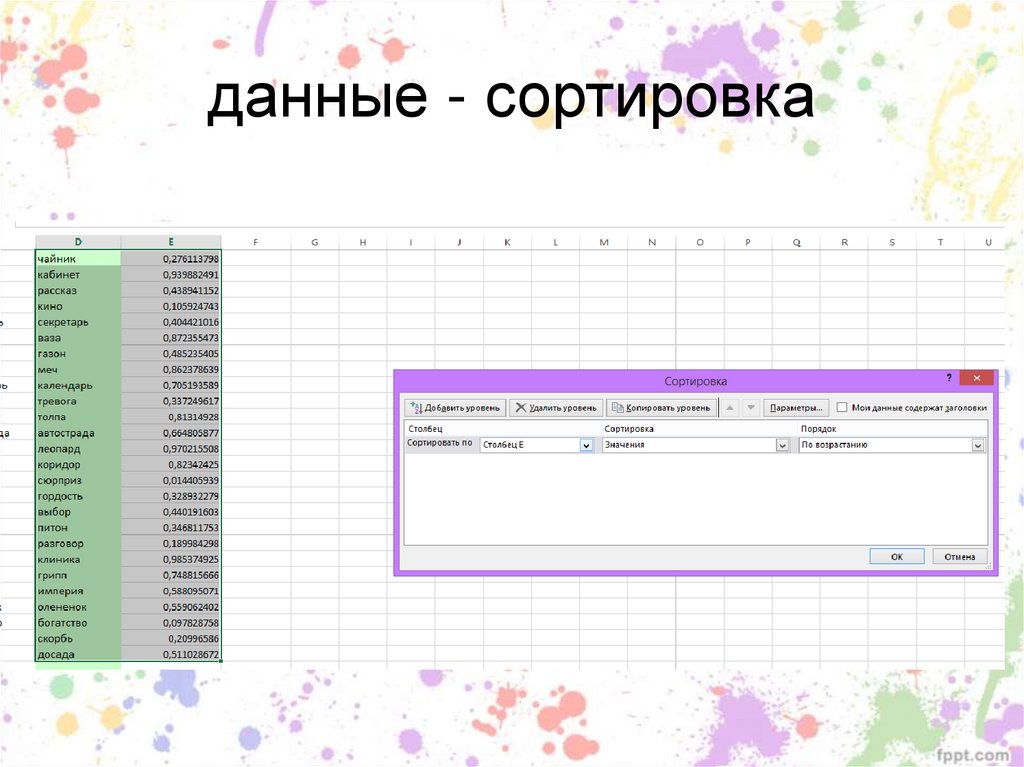
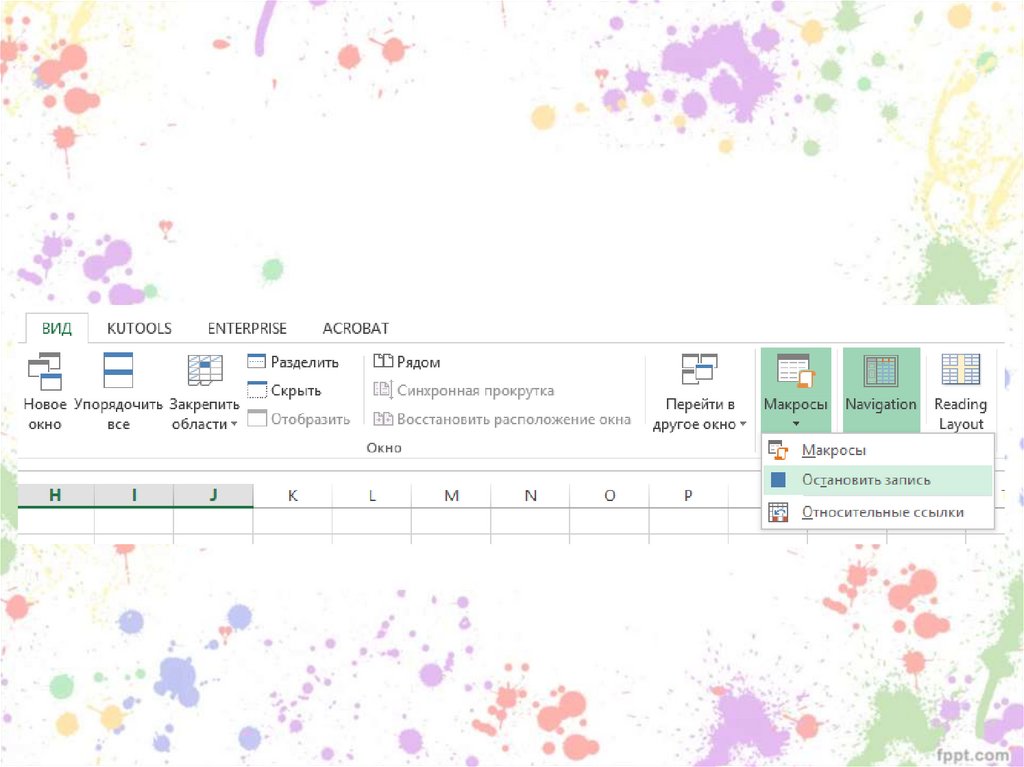
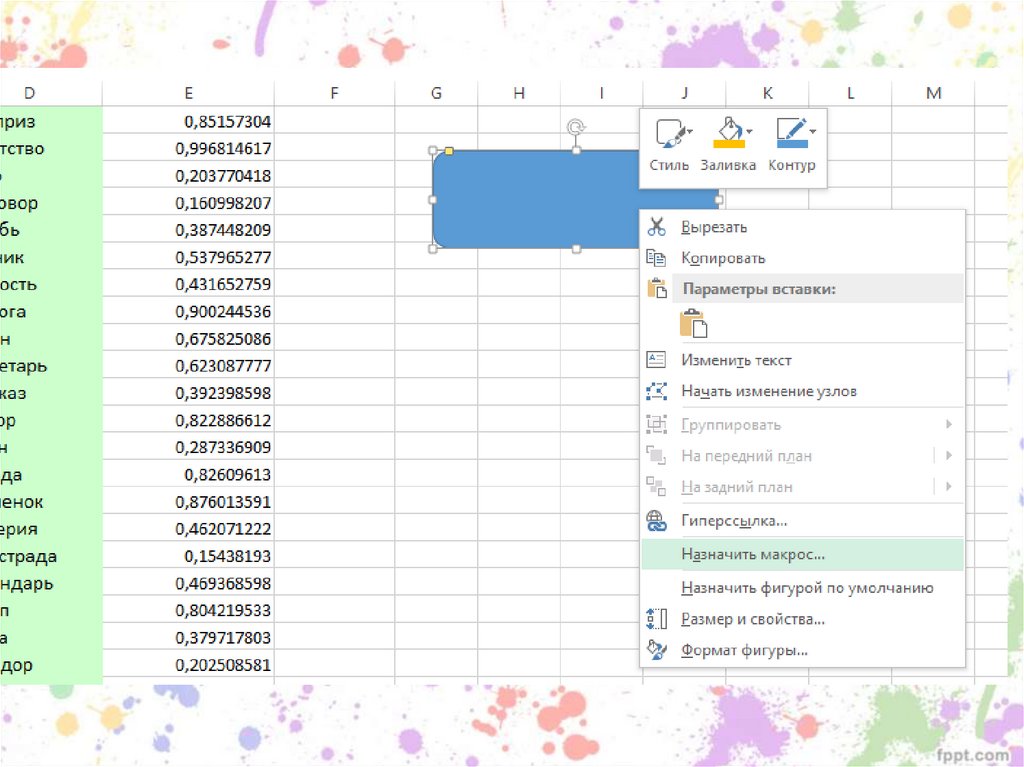
затем замедляется)
24.
• Ранний перенос• Поздний перенос
А Б Б А
25.
При использовании позиционноуравненной последовательности АББА
условия независимой переменной (А или
Б) оказываются связанными с раннимили -поздним переносом. Условие А
связано с поздним переносом, поскольку
оно получает «помощь» только на
четвертой пробе, а условие Б—с ранним,
на второй и третьей пробах.
26. ЭФФЕКТ КРАЯ
(явление, заключающееся в том, чтоиз расположенного в ряд
заучиваемого материала элементы,
находящиеся в начале и конце,
запоминаются быстрее, чем
элементы, находящиеся в середине)
27. Эффект ряда
• – эффект асимметричного переноса вмногоуровневом эксперименте, когда
род воздействий имеет несколько
уровней. Зависит от удаленности
предъявляемого испытуемому уровня
воздействия от концов ряда.
Объясняется адаптацией испытуемого к
предшествующему воздействию более
низкого или более высокого уровня, чем
предъявляемое.
28.
ЭФФЕКТ ЦЕНТРАЦИИ29.
• частичное проявление эффекта ряда,усиливающий действие независимой
переменной. Объясняется тем, что
уровням, предъявляемым в середине
последовательности, предшествуют и
более низкие и более высокие уровни
(при их случайном или позиционноуровневом чередовании).
30.
• в наиболее благоприятных условияхоказываются средние члены ряда.
31.
• Ошибка игрока или ложныйвывод Монте-Карло
отражает распространённое
ошибочное понимание
случайности событий.
32.
• Связана с тем, что, как правило,человек не осознаёт на
интуитивном уровне того факта,
что вероятность желаемого
исхода не зависит от
предыдущих исходов
случайного события.
33.
• Вероятность выпаденияследующего орла или решки
по-прежнему остаётся 1/2.
34. Как преодолеть все эти эффекты?
Допустим, что «А», «В», «С» ит.п. это разные условия, уровни
независимой переменной или
разные методики.
35. Как преодолеть все эти эффекты?
Допустим, что «А», «В», «С» и т.п. эторазные условия, уровни независимой
переменной или разные методики.
36.
AB
C
D
E
F
G
H
• Необходимо сбалансировать положение
каждой методики/пробы в
последовательности методик/проб в
выборке.
37. Позиционное уравнивание
АБ БА в интраиндивидуальномисследовании (интраиндивидуальное
позиционное уравнивание)
АБ
БА
–в
кроссиндивидуальном исследовании
(кроссиндивидуальное позиционное
уравнивание)
38.
• Позиционное уравнивание каждогоусловия внутри испытуемого требует
повторений условий – исследование
становится дольше. Получается полный
эксперимент. Позиция каждого условия
сбалансирована.
• Каждый следующий испытуемый
повторяет тот же эксперимент.
• Выборка используется для повышения
надежности результата, а не для
контроля систематического смешения.
39.
• Когда нет возможности проводить стольдлительные исследования переходят к
кроссиндивидуальному позиционному
уравниванию.
• Каждому испытуемому предъявляется
каждое из условий один раз.
40.
Таким образом мы не можем проверятьгипотезу на каждом отдельном испытуемом,
анализировать данные каждого испытуемого
как отдельную выборку, потому что позиция
каждого условия внутри индивида не
сбалансирована ( а значит данные на
каждом отдельном испытуемом подвержены
эффектам порядка).
Результаты каждого отдельного испытуемого
будут искажены систематическим
смешением.
41.
Полное позиционное уравнивание(все возможные последовательности
будут использованы хотя бы один раз).
Для этого вычисляется факториал
42.
Например, если у на 3 методики, то 3!=3*2*1=6,
Обозначим эти методики, как АBС
43. Полученные последовательности будут следующими
ABCACB
BCA
BAC
CAB
CBA
44.
• Нужно набирать выборку, кратную 6.Количество индивидов, выполняющих
методики в том или ином порядке,
должно быть равным.
Например:
A B C – 5 человек
A C B – 5 человек
B C A – 5 человек
B A C – 5 человек
C A B – 5 человек
C B A – 5 человек
45. Если у нас 6 методик?
• 6!=1*2*3*4*5*6=720Таким образом, чтобы предъявить все
возможные последовательности в
выборке, требуется 720 участников
46. Частичное позиционное уравнивание
Латинский квадрат(наблюдения расположены квадратом и
условия обозначаются латинскими буквами)
ABDC
BCAD
CDBA
DACB
47.
ABDCBCAD
CDBA
DACB
48.
ABDCBCAD
CDBA
DACB
49.
АБВГДЕВДГАЕБ
ДВАЕБГ
БГЕВАД
ГЕБДВА
ЕАДБГВ
50. Альбрехт Дюрер «Меланхолия»
51.
• Каждая буква встречается в каждойстроке и каждом столбце один раз.
52.
• Латинский квадрат, у которогобуквы в первой строке и первом
столбце расположены в
алфавитном порядке, называется
стандартным.
ABCD
BADC
CDAB
DCBA
53. Кембридж
Окно в честь Фишерас латинским
квадратом 7-го
порядка.
54.
положение каждой методики/пробы впоследовательности методик/проб
должно быть сбалансировано.
A=2,5
B=2,5
C=2,5
D=2,5
1
2
3
4
55.
• Стандартный латинский квадратможно получить, если расположить
буквы в первой строке в алфавитном
порядке, а в каждой из последующих
строк со сдвигом на одно положение
влево по сравнению с предыдущей
56.
Правильный латинский квадрат-частота появления каждого
экспериментального условия одинакова
для всех последовательных позиций
сбалансированный латинский квадрат
•-каждому условию предшествует, а также
следует за ним каждое другое условие
строго один раз
57.
• Эффекты последовательности,связанные с влиянием одного уровня
независимой переменной на другой, не
снимаются этими планами, но
контролируются путем усреднения
полученных показателей зависимой
переменой по каждому уровню,
занимающему разное место в каждой
последовательности.
58. Построим латинский квадрат для 6 экспериментальных методик (или условий, или уровней независимой переменой)
ABCDEF59.
• Первый ряд латинского квадратастроится следующим образом:
AB “X” C “X-1” “X-2” (D)
A означает первое экспериментальное
условие, а «Х» -последнее.
«Х» →F
“X-1” →E
Таким образом
Первый ряд: ABFCED
60. Строим второй ряд
Для этого прямо под каждой буквойпервого ряда во втором ряду помещаем
следующую по алфавиту букву
(единственное исключение буква F.
Дойдя до нее нужно вернуться в начало
алфавита и поместить под ней букву A.
Первый ряд: ABFCED
Второй ряд: BCADFE
61. Пользуясь этим правилом можно построить все остальные ряды
ABFCEDBCADFE
CDBEAF
DECFBA
EFDACB
FAEBDC
62.
ЛАТИНСКИЙ КВАДРАТДЛЯ 3Х3 (третьего порядка)
ЛАТИНСКИЙ КВАДРАТ
4Х4 (четвертого порядка)
ABC
BCA
CAB
ABDC
BCAD
CDBA
DACB
63.
ЛАТИНСКИЙ КВАДРАТ5Х5
ЛАТИНСКИЙ КВАДРАТ
ДЛЯ 7Х7
ADBEC
DACBE
CBEDA
BEACD
ECDAB
ABCDEFG
BCDEFGA
CDEFGAB
DEFGABC
EFGABCD
FGABCDE
GABCDEF
64.
• Выборка должна быть кратнаколичеству уровней или методик или
условий.
65. ТАБЛИЦА СЛУЧАЙНЫХ КВАДРАТОВ
Для исследования определенныйлатинский квадрат выбирается
случайным образом из перечня
возможных латинских квадратов
заданного размера.
66.
3х3 4х45х5
6х6
7х7
рхр
Число
стандартных
квадратов
1
4
56
9408
16942080
-
Общее число
латинских
квадратов
12
576
161280
81885120
0
6147941990400
0
P!(p-1)!xчисло
стандартных
квадратов
67. Генератор латинских квадратов
http://hamsterandwheel.com/grids/index2d.php68.
• http://statpages.info/latinsq.html• Списки латинских квадратов,
сгенерированных в программе R
69.
• Существует ряд игр, в которыхиспользуются латинские квадраты.
Наиболее известна из них судоку. В ней
требуется частичный квадрат дополнить
до латинского квадрата 9-го порядка,
обладающего дополнительным
свойством: все девять его подквадратов
содержат по одному разу все
натуральные числа от 1 до 9.
70.
• Если бы все эффекты переноса былисвязаны с непосредственно
предшествующим уровнем,
сбалансированный квадрат был бы
очень эффективен.
• Нет способа проверить, действительно
ли это так.
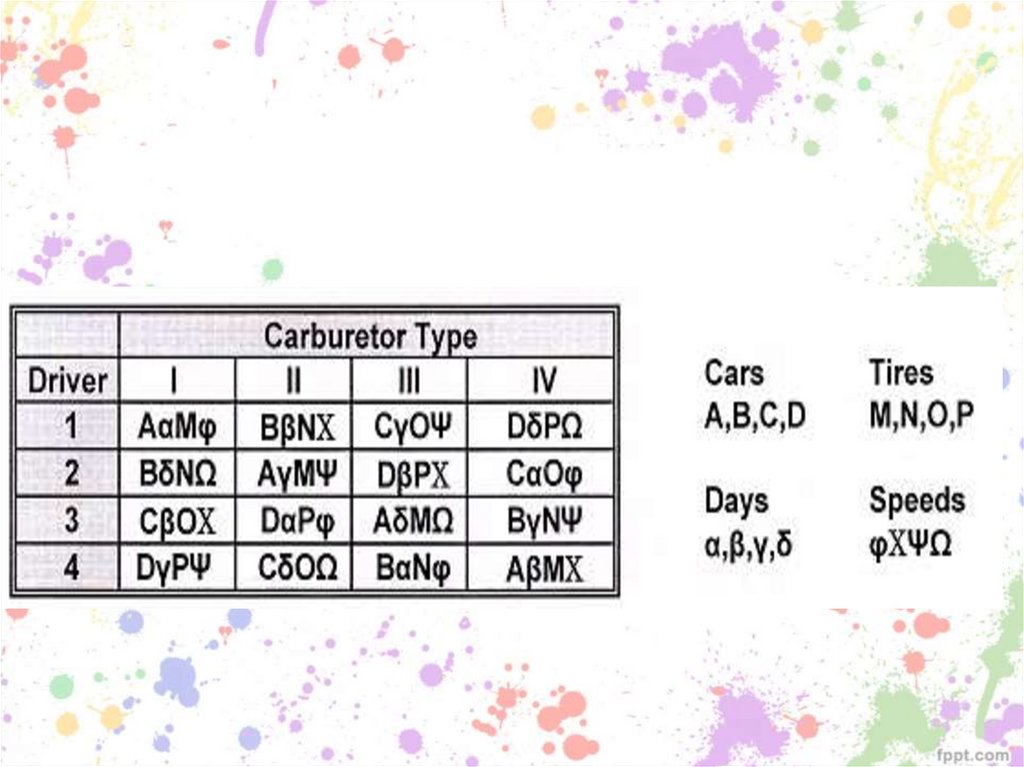
71. Греко-латинский квадрат
• Если взять один латинский квадрат pxp иналожить его на другой латинский квадрат
pxp, в котором условия обозначим не
латинскими, а греческими буквами.
• Если при наложении каждая греческая
буква встречается с каждой из латинских
букв один и только один раз, то говорят,
что такой квадрат ортогонален.
72.
СТОЛБЕЦСТРОКА
1
2
3
4
1
Aα
Bδ
Cβ
Dγ
2
Bβ
Aγ
Dα
Cδ
3
Cγ
Dβ
Aδ
Bα
4
Dδ
Cα
Bγ
Aβ
73.
• С его помощью можно исследоватьвлияние на зависимую переменную
нескольких независимых. Суть его в
следующем: к каждой латинской группе
плана присоединяется греческая буква,
обозначающая уровни еще одной
переменной.
74.
• При наложении трех и болееортогональных латинских
квадратов рхр образуется
гиперквадрат рхр
75.
76. Обратное позиционное уравнивание (реверсивное)
ABBA
Только 2 последовательности
ABCD любая последовательность
DCBA обратная ей
A=(1+4)/2=2,5 –среднее положение методики «А» в
последовательности методик.
D=(4+1)/2=2,5
B=(2+3)/2=2,5
C=(3+2)/2=2,5
77.
• Одна и та же средняя позиция.• Хороший контроль влияния
последовательности, только если
эффект переноса однороден.
• ABCD
• A влияет на B, как B на C, и т.д.
78. Чередование
• ABABAB• Случайный порядок не всегда есть
возможность применить.
79.
• Однородный и симметричный переносыустраняются при регулярном
чередовании и позиционном
уравнивании (интраиндивидуальный
эксперимент), а также при реверсивном
уравнивании (кроссиндивидуальный
эксперимент).
80.
• Несимметричный перенос усредняетсяприменением случайной
последовательности.
81. Случайный порядок
• если большое количество проб• пробы достаточно короткие
• когда испытуемый не должен знать о
состоянии независимой переменной в
каждой данной пробе
82.
• исключается всякая возможностьсистематического смешения
независимой переменной с факторами
времени, поскольку в случайной
последовательности никакой системы
не существует.
• С увеличением проб повышается
надежность эксперимента.
83.
случайный ≠ беспорядочный84.
• В случайно выбранном наборепоследовательностей маловероятно,
что каждый уровень окажется в каждой
позиции равное число раз.
• Нежелательные последствия
неоднородного переноса будут
продолжать существовать.
85. Таблица случайных чисел в EXCEL
СЛЧИС RANDСЛУЧМЕЖДУ RANDBETWEEN
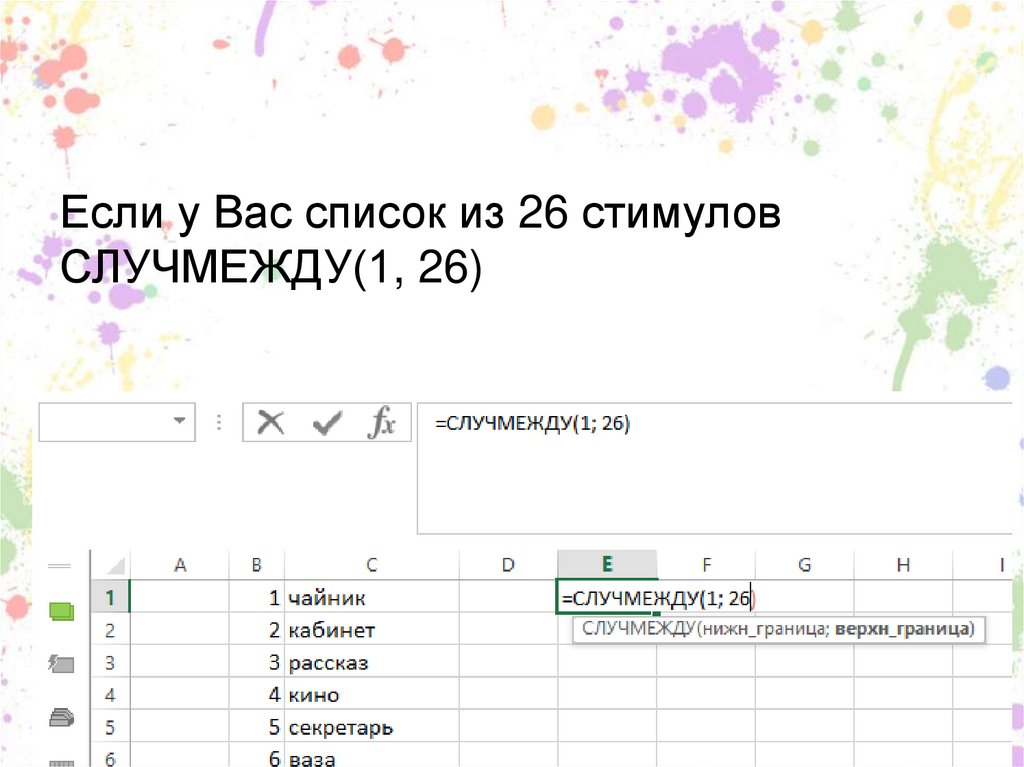
86.
Если у Вас список из 26 стимуловСЛУЧМЕЖДУ(1, 26)
87.
88.
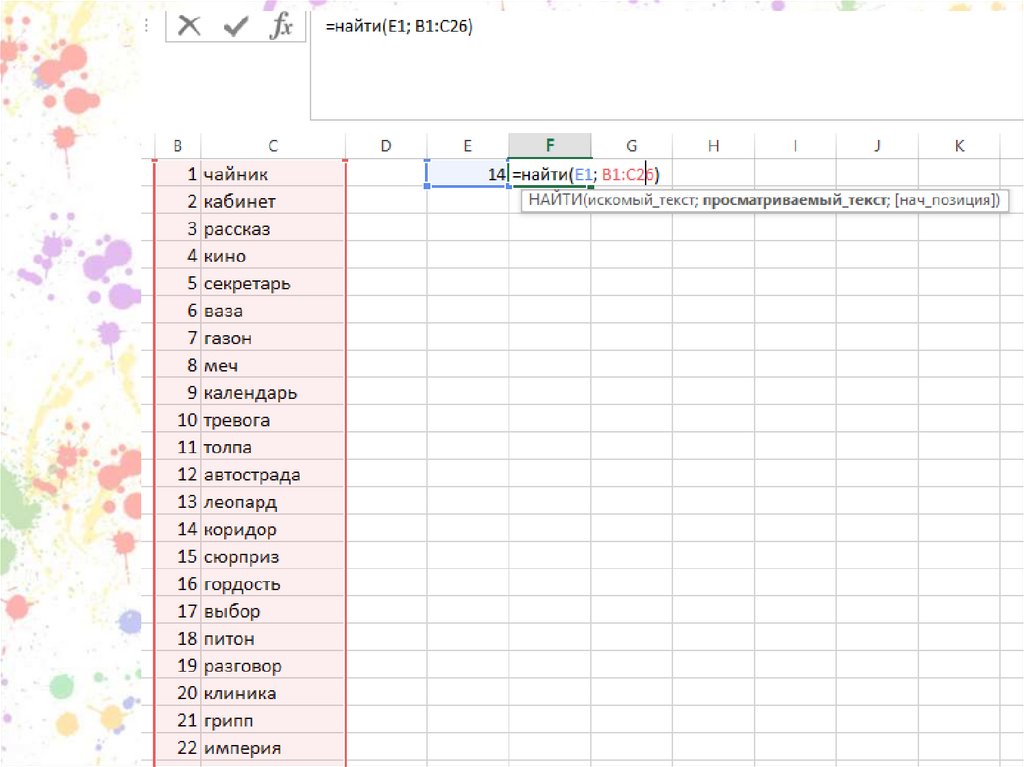
• НАЙТИ VLOOKUP• Найти того, кто будет в случайном
списке стоять на 1 позиции
НАЙТИ(выделяем ячейку с формулой
рандомизации, пронумерованный
список, начальную позицию).
89.
• F9новый случайный порядок.
90.
• Если исследование проводится безиспользования компьютерных программ
и нужно каждому испытуемому
предъявлять стимульный материал в
новом случайном порядке
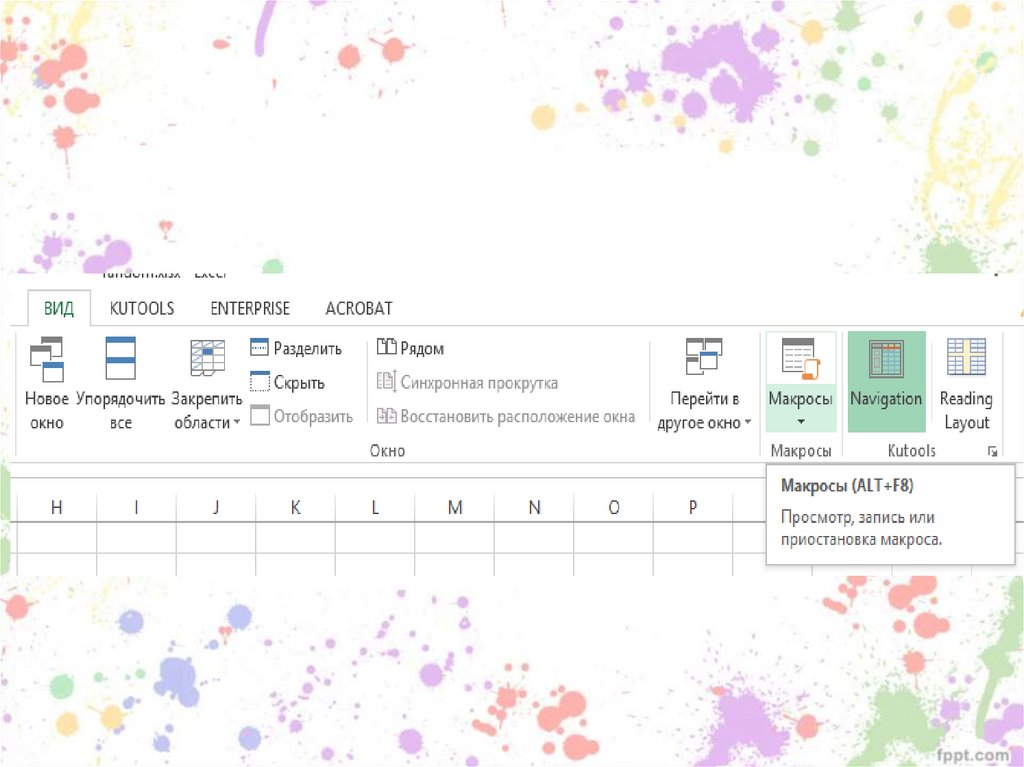
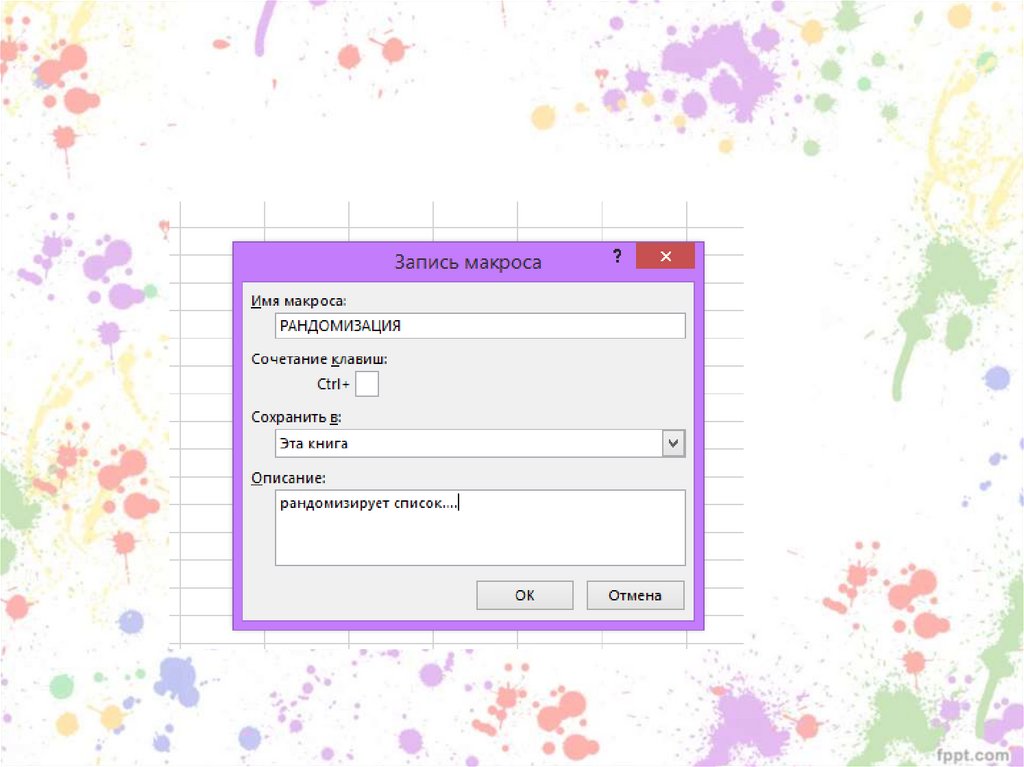
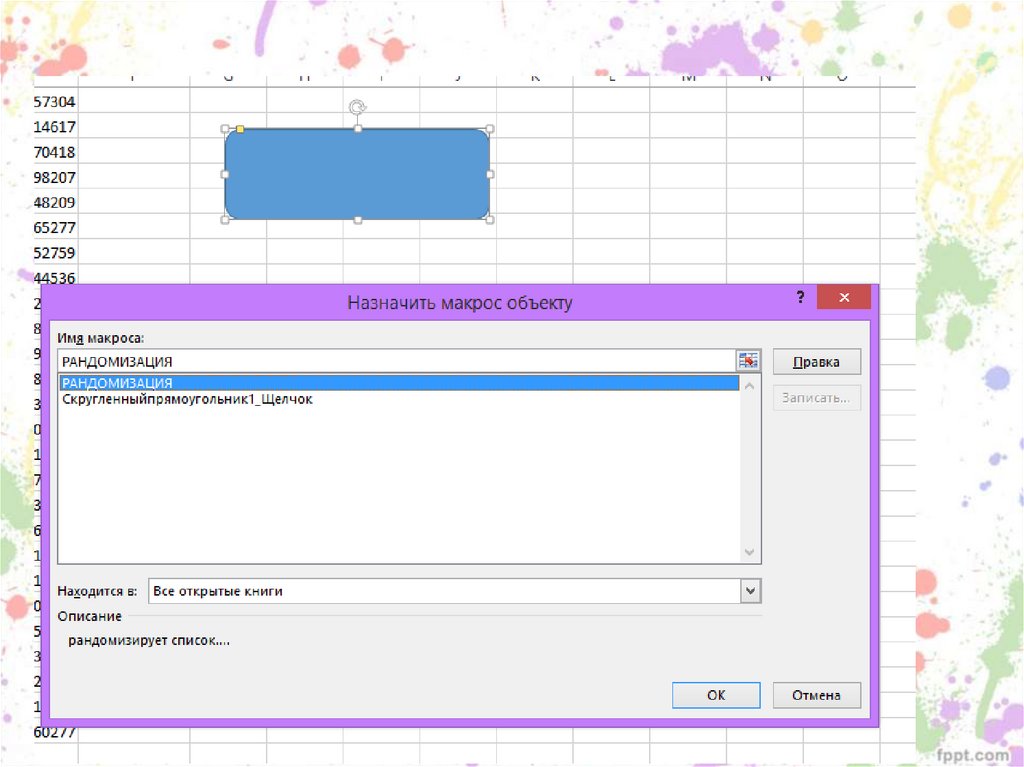
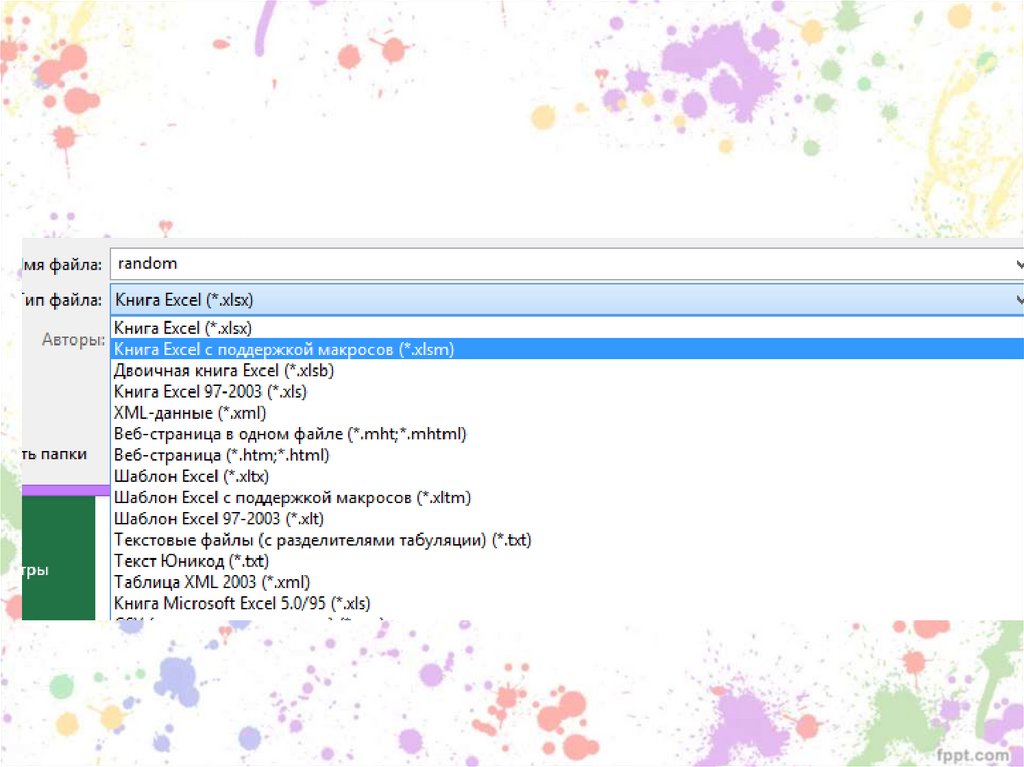
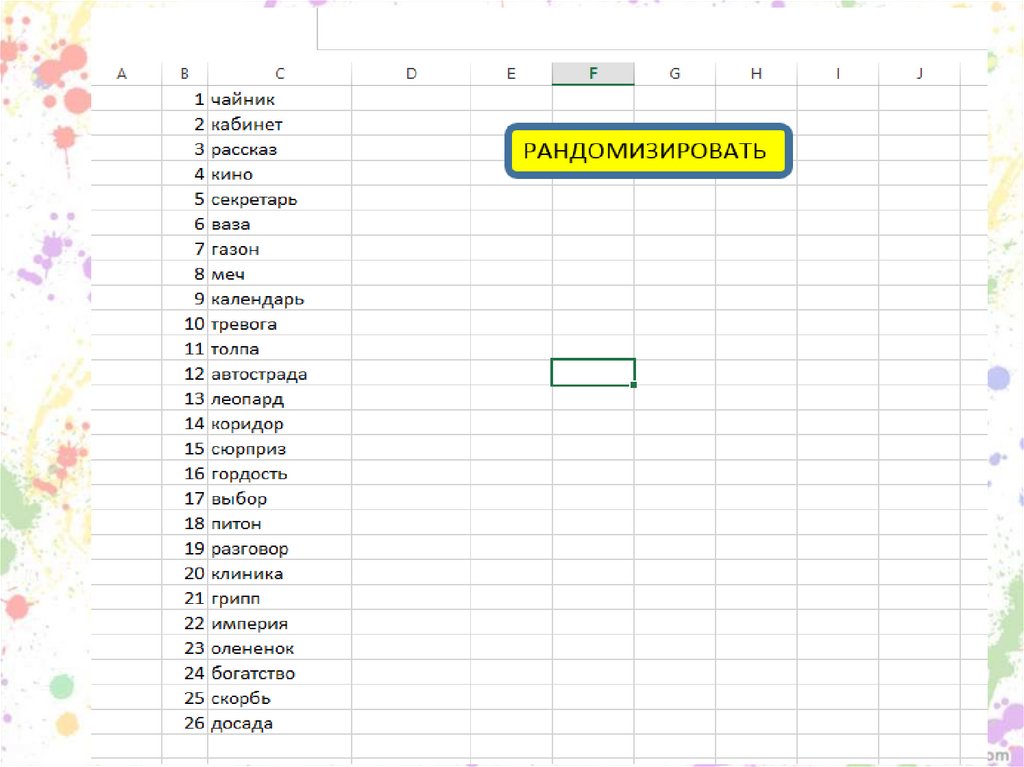
91. Макрос для создания списков в случайном порядке
92.
93.
94.
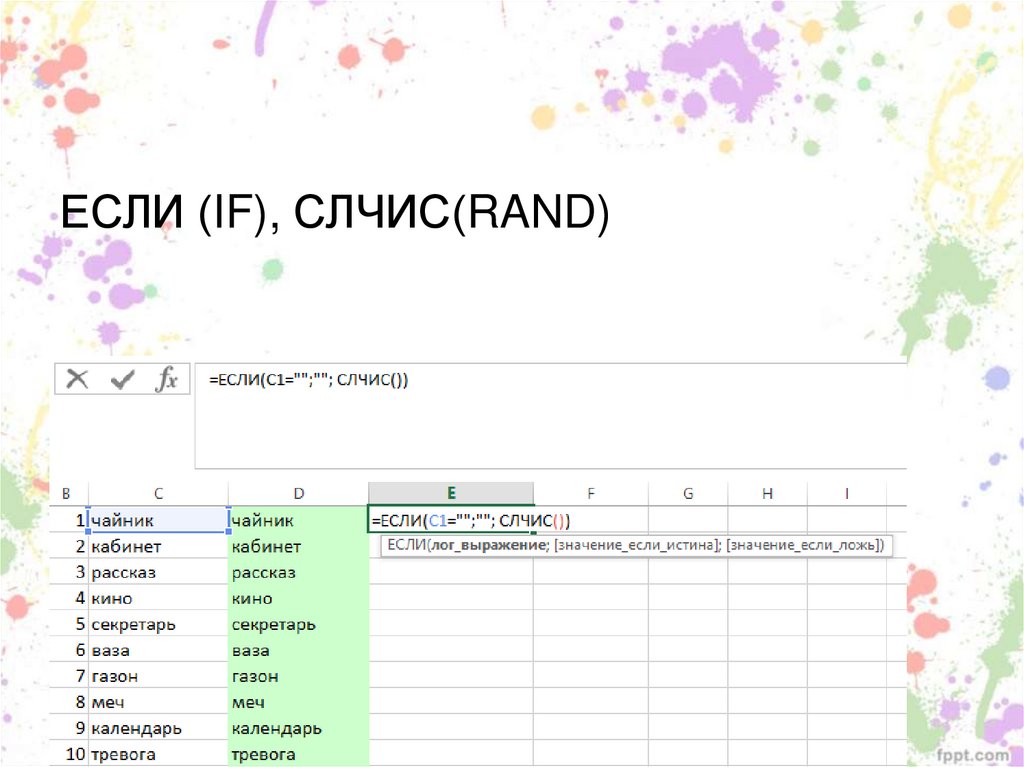
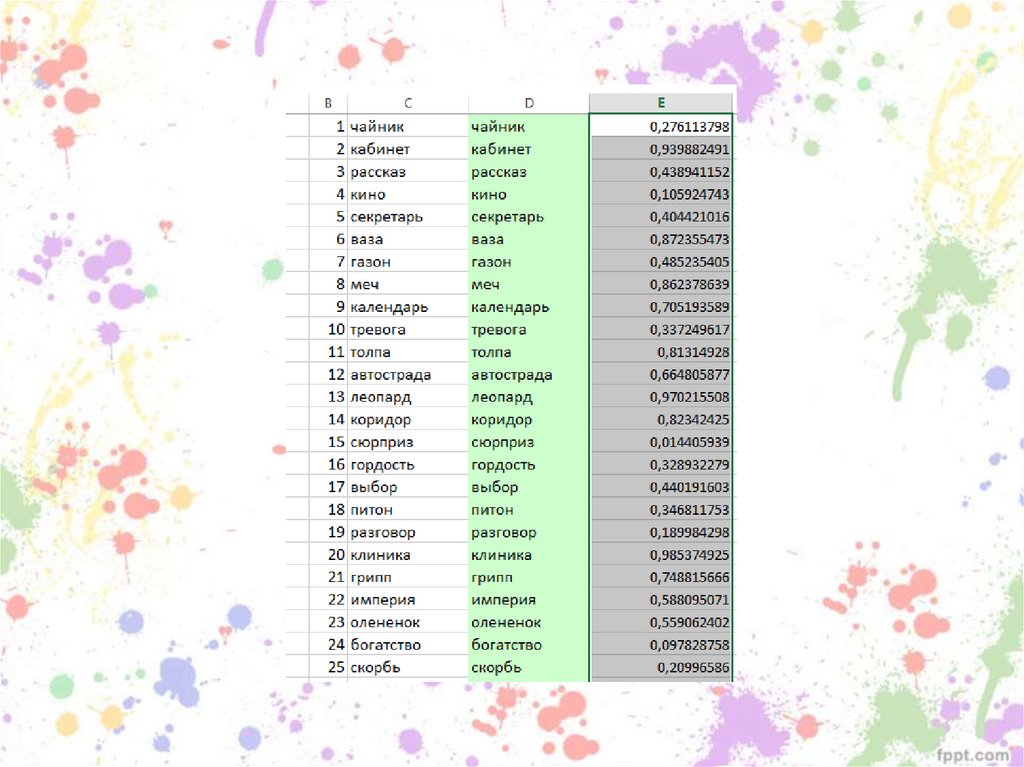
ЕСЛИ (IF), СЛЧИС(RAND)95.
96. данные - сортировка
97.
98.
99.
100.
101.
102.
103.
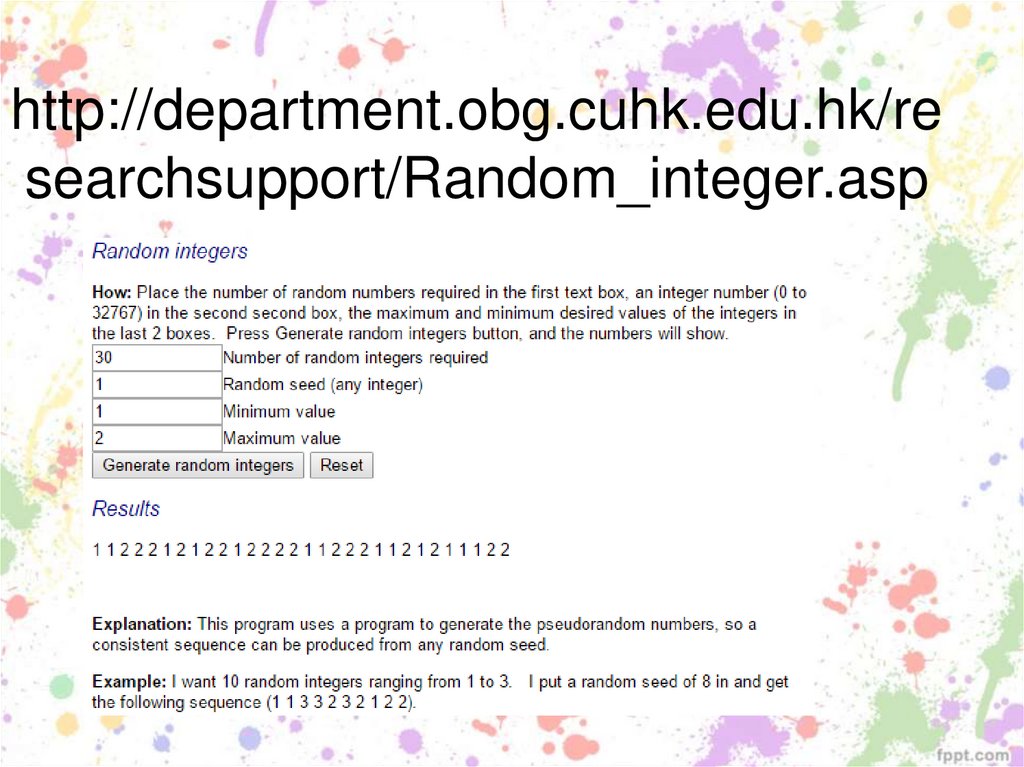
104. http://department.obg.cuhk.edu.hk/researchsupport/Random_integer.asp
http://department.obg.cuhk.edu.hk/researchsupport/Random_integer.asp
105.
В профессиональных психологическихкомпьютерных программах есть опция, с
помощью которой можно предъявлять пробы в
случайном порядке (e-prime, PXLab)
106. Псевдослучайный (квазислучайный) порядок
Если какие-то методики/пробы не должныидти друг за другом в последовательности.
Квазислучайный контроль последовательности включает
нарушение рандомизации, поскольку при составлении
общей последовательности проб дополнительно
выравнивается (балансируется) их представленность в
разных ее частях. В противоположном случае случайно
может проявиться неравномерность в распределении
более высоких и более низких уровней фактора (по
номерам предъявлений уровней).
107.
• Пример: пункты опросника могут бытьпредставлены в списке в
псевдослучайном порядке так, чтобы
вопросы, принадлежащие одной и той же
шкале не шли друг за другом.












































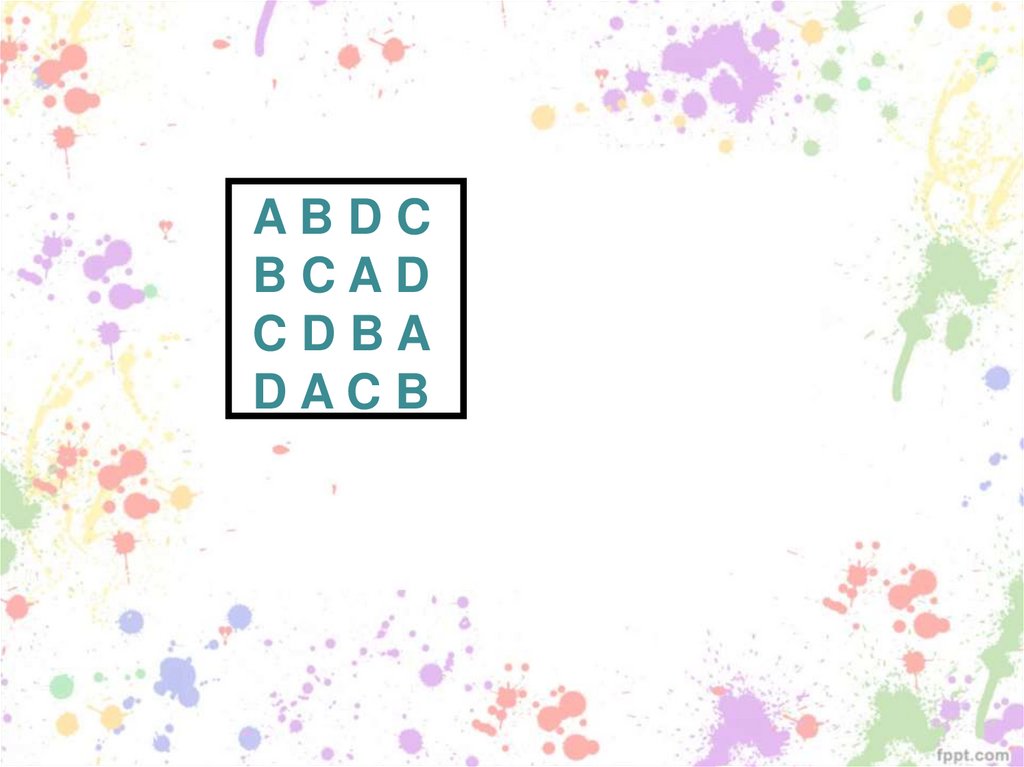













































 Образование
Образование