Похожие презентации:
Понятие интеграла
1. Понятие интеграла
2. где F(x) – одна из первообразных для функции f(x)
Площадь криволинейной трапеции можновычислить по формуле
где F(x) – одна из первообразных для функции
f(x)
3. (читается: «Интеграл от а до b эф от икс дэ икс»),
Разность F(b) – F(a) называют интегралом отфункции f(x) на отрезке [a;b] и обозначают:
b
f x dx
a
(читается: «Интеграл от а до b эф от икс дэ икс»),
4. f(x) -
bf x dx
a
знак интеграла
f(x) - подынтегральная функция
dx – элемент интегрирования
a – нижний предел интегрирования
b – верхний предел интегрирования
5. Т.е.
bf x dx F (b) F (a)
a
Данную формулу называют формулой
Ньютона-Лейбница в честь создателей
дифференциального и интегрального
исчисления.
6. При вычислении интегралов удобно ввести обозначение:
F (b) F (a) F ( x)b
a
Тогда формулу Ньютона-Лейбница
можно записать в виде:
7. Например:
1х
а ) х dx
5
2
5
4
1 2
5
5
5
1
2
1 32
33
6,6
5 5
5
5
8. Например:
х2
б ) 8 2 х х dx 8 х х
3
2
64
8
32 16 16 4
3
3
4
2
3
4
2
64
8
72
48 12 60
3
3
3
60 24 36
9. Например:
3dx
в) 3
x
1
3
1
2
x
x dx
2
3
3
1
1 1
1 1
1 3
2 1
18 2
18 2
2x
1 9
8
4
18 18 18 9
10. Например:
1г ) sin 3 х dx cos 3x
3
4
4
0
4
4
0
1 3
cos
cos 0
3 4 4
4
1
1 0 2 2
cos cos
6
3
2
3 2
4
11. Например:
хx
x
д) 2 sin сos dx sin 2 dx
2
2
2
0
0
0
0
sin xdx cos x
1 1 2
cos cos 0
12. Вычислите интегралы:
51) 3dx
2
3
2) х dx
3
1
2
3) 2 х 3 dx
3
1
4) 5 4 х dx
2
13. Вычислите интегралы:
25) 2 х 3x dx
0
1
2
6) 2 х 3x 1 dx
3
2
7) х 2 sin x dx
2
2
0
8) х 3соsx dx
0
3
14. Вычислите интегралы:
73
dx
9) 2
x
2
2
dx
10)
2
1 2 х 1
11)
2
4
dx
x 2
2
12) sin 2 xdx
4
15. Вычислите интегралы:
23
x
x
15) sin cos dx
4
4
0
x
13) 3соs dx
2
0
4
14) сos x sin x dx
0
2
2
2
2
16) sin x cos xdx
0






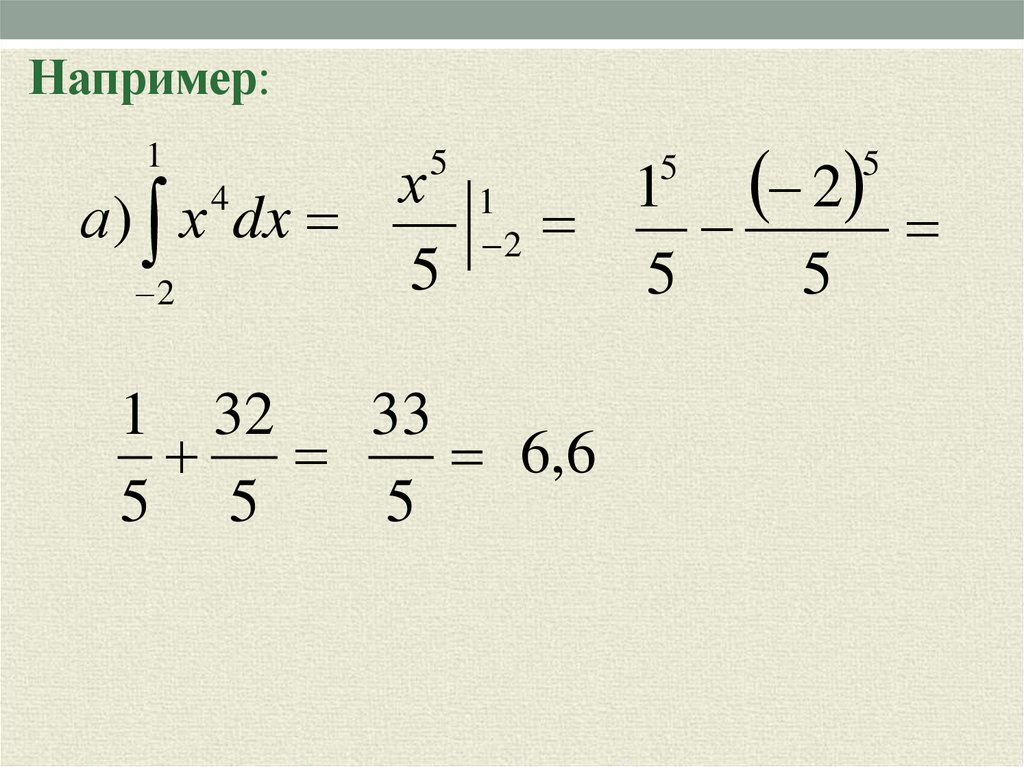


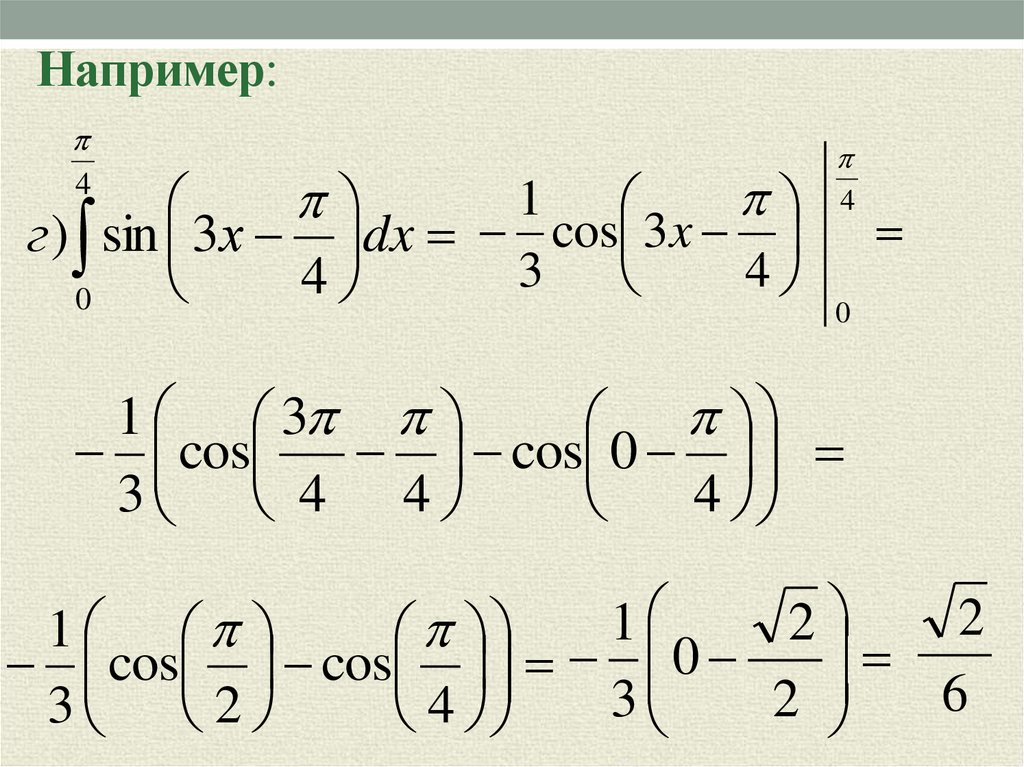





 Математика
Математика








